The quantum reason why neutral atoms first formed

In order for you to exist, a lot of things had to happen beforehand. Planet Earth needed to come into existence, complete with the organic ingredients from which life could arise. In order to have those ingredients, we need for many previous generations of stars to have lived-and-died, recycling the elements formed within them back into the interstellar medium. For those stars to live, large quantities of neutral, molecular gas had to collect in one place, collapsing under its own gravity to fragment and form stars in the first place. But in order to make those stars — even the very first stars — we first need the Universe to create stable, neutral atoms.

In a Universe that begins with a hot Big Bang, this isn’t necessarily so easy! A few minutes after the hot Big Bang, our Universe was filled with protons and a small but important population of more complex light atomic nuclei, an equal number of electrons to the total number of protons, a large number of neutrinos that don’t interact with any of them, and about 1.4 billion photons for every proton-or-neutron present. (There’s also dark matter and dark energy, but like neutrinos, they’re not important to this part of the story.)

So how long does it take these protons and other nuclei to combine with electrons, stably forming neutral atoms? A whopping 380,000 years. But that’s only because of a very special quantum reason. Without it, things would have taken much longer. Here’s the science behind it.

The unique prediction of the Big Bang model is that there would be a leftover glow of radiation permeating the entire Universe in all directions. The radiation would be just a few degrees above absolute zero, would be the same magnitude everywhere, and would obey a perfect blackbody spectrum. These predictions were borne out spectacularly well, eliminating alternatives, but pointing toward a very early, hot, dense state where these photons were energetic enough to, for a time, prevent the stable formation of any neutral atoms.

In the early stages of the Universe, things were very dense, very uniform, and very hot. That last part — very hot — has two important consequences that we cannot ignore.

1. Particles with non-zero rest masses move very quickly, even close to the speed of light, and when they collide with one another, those are high-energy collisions, capable of breaking apart anything that isn’t bound together tightly enough.
2. Particles that are massless, like photons, although they always move at the speed of light, possess very large amounts of kinetic energy as well, which means they have very short wavelengths and also initiate high-energy collisions that are capable of breaking apart any bound structures they run into.

This is important, because there are lots of photons for every proton, atomic nucleus, and electron in the Universe. The way you make atoms is to have an electron stably bind to a nucleus in equal numbers to the number of protons in its nucleus, and then the way you keep those atoms is to have them survive collisions between particles and interactions with photons without being blasted apart.

In the hot, early Universe, once atomic nuclei have been created, making a neutral atom is easy, but destroying that neutral atom and converting it back into a bare nucleus and free electrons is both inevitable and fast. Neutral atoms are formed, but they aren’t stable in this environment.

Although we normally conceive of atoms as nuclei with electrons orbiting them, if the environment in which an atom is placed has a magnetic or electric field within it, the orbital properties of the electrons, including the energy levels that they occupy, will change. As a result, the photons they emit or absorb will be of different wavelengths than if the field were removed.

That will change if the Universe becomes cool enough so that, once you form a neutral atom, they won’t immediately be blasted apart back into bare nuclei and free electrons once again. Most of the normal matter in the Universe is made of hydrogen — in fact, if you count atoms by number, 92% of all atoms in the Universe at this point are hydrogen atoms — and hydrogen is one of the most well-studied atoms of all.

One of the amazing things about it?

The way it’s different from an unbound proton and electron. When electrons are unbound from protons, then photons — particles of light — of absolutely any wavelength and energy can interact with and scatter off of the electrons. A free electron in a sea of (much more numerous) photons gets bounced around, like a pinball, constantly.

When you have a stable, neutral atom, however, all of that changes. Only photons of a very specific set of wavelengths can be absorbed, because the possible energy states of an electron within a bound atom are finite in number and follow a specific set of patterns and rules. In other words, they are quantized.

A variety of energy levels and selection rules for electron transitions in an iron atom. There are only a specific set of wavelengths that can be emitted or absorbed for any atom, molecule, or crystalline lattice. Although each atom has a unique spectrum of energies, all atoms share certain quantum properties.

The catch is this: if you hit a neutral atom with a photon that’s high enough in energy, then regardless of what the quantum rules are that govern this atom’s energy levels, the electron will absorb the photon and will get kicked out of the atom entirely, ionizing it once again.

For a hydrogen atom, the key energy threshold that will ionize even a ground-state electron bound to its central proton is well known: 13.6 electron-volts, or 13.6 eV for short.

One tempting (but incorrect!) short-cut to take is to say, “A-ha, I know about Boltzmann’s constant, and that provides a conversion factor between energy and temperature. Therefore, all I have to do is convert the energy I need — 13.6 eV — into a temperature, using Boltzmann’s constant, and once the Universe cools past that point, I’ll make neutral atoms.”

If you take that shortcut, you get a temperature for the Universe of ~158,000 K, and you’d conclude that above that temperature, all of your hydrogen is ionized, while below that temperature, it all becomes neutral. Counting forward from the Big Bang, that temperature is reached just ~220 years after the hot Big Bang. But if we were to look at the Universe back then, we’d find that not only were all of the atoms not neutral and stable, but rather absolutely none of them were.

In the hot, early Universe, prior to the formation of neutral atoms, photons scatter off of electrons (and to a lesser extent, protons) at a very high rate, transferring momentum when they do. After neutral atoms form, owing to the Universe cooling to below a certain, critical threshold, the photons simply travel in a straight line, affected only in wavelength by the expansion of space.

Our short-cut led us astray, and the reason is this: photons are just like any other particle, and when you have a large number of them bouncing off of the other particles in your system, they don’t all have exactly the same energy. Instead, there’s a distribution of energies that they follow, with some of them being higher-than-average in energy and some of them being lower-than-average in energy. Sure, it’s true that when we look at the Universe ~220 years after the start of the hot Big Bang, the average temperature of the Universe is ~158,000 K, and the average energy of each photon is 13.6 eV. But under those conditions, 100% of the atoms in the Universe remain ionized.

Don’t forget: there are just over 1.4 billion photons for every electron in the Universe, and electron-photon collisions are extremely rapid when the Universe is hot and dense. If even just one out of every billion photons crosses over that key energy threshold — if it carries more than 13.6 eV of energy — and it strikes a neutral hydrogen atom, that atom will immediately become ionized again.

You might want to forget all about atoms and just wait until the Universe becomes sparse enough so that the photons no longer encounter electrons efficiently enough to bounce off of them regularly. But without atoms, the Universe wouldn’t drop to a low enough density to become transparent to the photons within it until more than 1 billion years after the Big Bang.

This simplified animation shows how light redshifts and how distances between unbound objects change over time in the expanding Universe. Note that the objects start off closer than the amount of time it takes light to travel between them, the light redshifts due to the expansion of space, and the two galaxies wind up much farther apart than the light-travel path taken by the photon exchanged between them.

Instead, you can consider the question of, “Alright, what happens if I just wait long enough so that fewer than 1-in-1.4 billion photons now exceed that critical 13.6 eV threshold? Will I now stably form neutral atoms?”

As the Universe continues to age, it also expands, which stretches the wavelength of every photon traveling through it. If we want to ask how old the Universe is when only 1-in-1.4 billion photons reaches or exceeds 13.6 eV in energy, that threshold is crossed when the Universe is only a little more than 100,000 years old. But still, when we examine the Universe at that time, the neutral atoms that are formed aren’t stable, but rather get blasted apart again in short order.

Why is this?

The same annoying rule about quantum mechanics and energy levels in atoms has now come back to haunt us. You have to remember that, yes, if you hit an electron with a photon of the right energy, it will either excite the electron up to a higher-energy state or, with enough energy, will knock it right off of the atom it’s bound to. But the reverse is also true: whenever an electron becomes bound to a nucleus, it spontaneously cascades down the various energy levels, emitting photons of specific wavelengths as it does.

Electron transitions in the hydrogen atom, along with the wavelengths of the resultant photons, showcase the effect of binding energy and the relationship between the electron and the proton in quantum physics. The Bohr model of the atom provides the coarse (or rough, or gross) structure of the energy levels, but this already was insufficient to describe the fine and hyperfine structure, which had been seen decades prior.

Two things are then of paramount importance to know about atoms in an excited state.

1. They are much more vulnerable to being ionized by photons, as even the next-to-ground-state only requires a photon of 3.4 eV to come along and ionize hydrogen, as opposed to 13.6 eV in the ground state. To remain stable against ionization, atoms need to reach the ground state; until they do, they’re not safe.
2. But in order to reach the ground state, electrons need to de-excite from a higher energy level, and the act of de-excitation produces a high energy photon — of between 10.2 and 13.6 eV — that can easily be re-absorbed by the next ground-state hydrogen atom it encounters.

In other words, even once the Universe cools sufficiently so that the background photons left over from the Big Bang won’t ionize a hydrogen atom, the newly-formed hydrogen atoms are vulnerable to photons produced by the act of other hydrogen atoms becoming neutral. The key isn’t just to form neutral hydrogen; the key is to form neutral hydrogen that’s stable: that won’t be reionized in short order from the surrounding radiation, even radiation that comes from the production of other neutral hydrogen atoms.

At early times (left), photons scatter off of electrons and are high-enough in energy to knock any atoms back into an ionized state. Once the Universe cools enough, and is devoid of such high-energy photons (right), they cannot interact with the neutral atoms, and instead simply free-stream, since they have the wrong wavelength to excite these atoms to a higher energy level. However, when you make a neutral atom in the ground state, you emit a high-energy photon from that process, and if a new atom then absorbs that photon, it gets excited and becomes easily ionized. This “bottleneck” must be passed, and cosmic expansion helps, but isn’t the only (or even the dominant) factor.

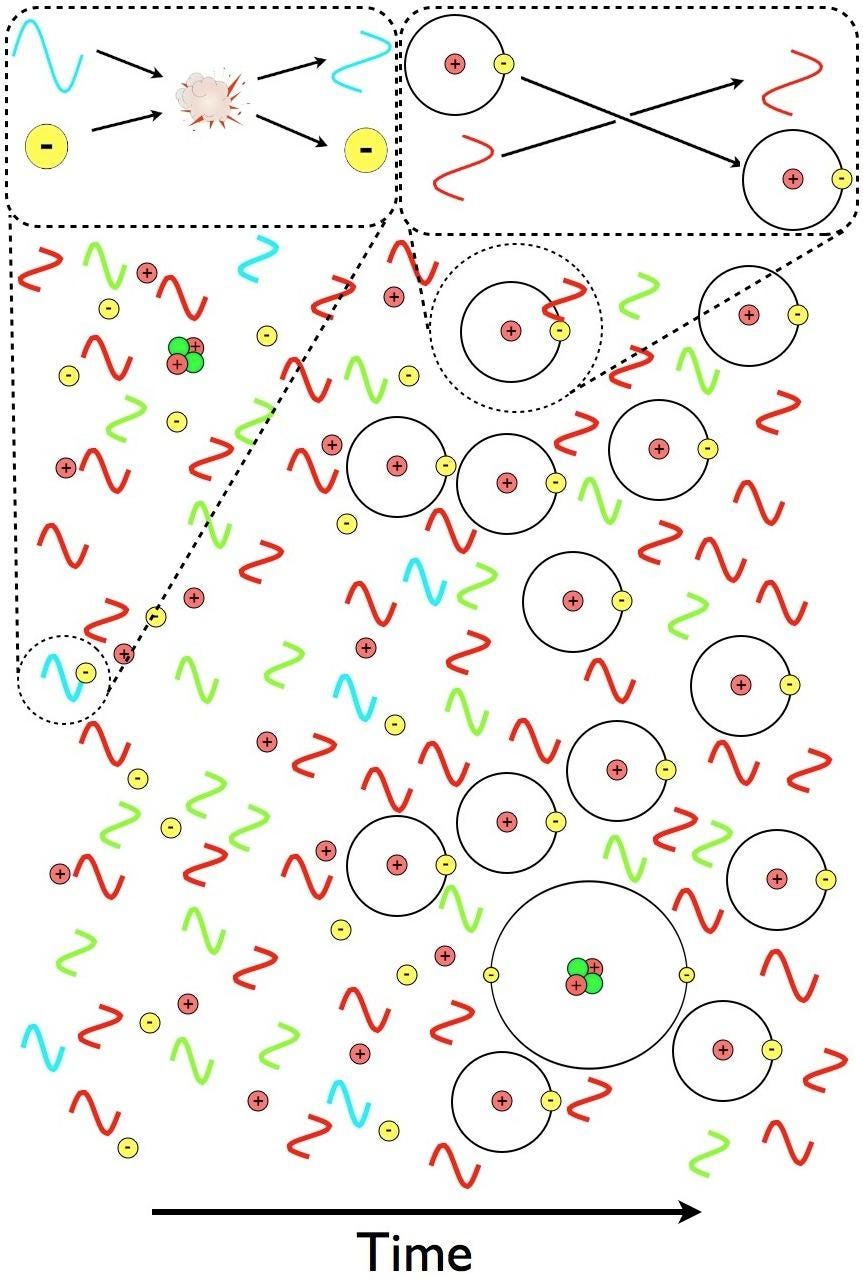
“A-ha,” you might think. “That’s easy; just wait until the average distance between the atoms becomes great enough so that while the high-energy photon produced by one neutral atom travels toward the next atom, the cosmic expansion shifts it to a longer wavelength: long enough so that it can’t be reabsorbed.”

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

This time, your thought is pretty good, because this process really does occur, and it does contribute to a fraction of the hydrogen atoms present in the Universe becoming neutral. This time, if this were the only process we relied on to make neutral hydrogen atoms, we’d get closer to the actual answer, calculating that it would take somewhere around 800,000 years for the atoms in the Universe to become neutral. That corresponds to a temperature of the Universe of about ~1900 K, which is at least a reasonable figure.

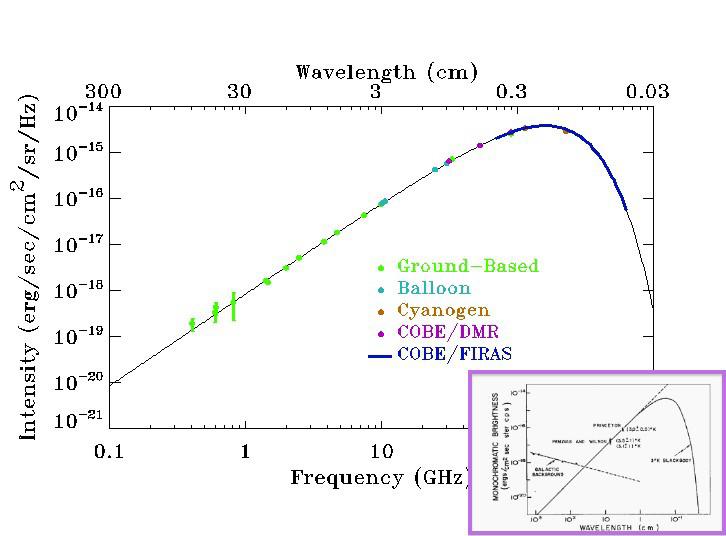
But it’s not right. The Universe, as observed by many ground-based instruments, telescopes, receivers, and space-based satellites, became neutral back when the Universe was only ~380,000 years old and was more like ~3000 K in temperature. It’s a gradual process, taking more than 100,000 years to complete, but it happens much more rapidly than simply folding in cosmic expansion and atomic physics would lead you to believe.

The energy levels and electron wavefunctions that correspond to different states within a hydrogen atom, although the configurations are extremely similar for all atoms. The energy levels are quantized in multiples of Planck’s constant, but the sizes of the orbitals and atoms are determined by the ground-state energy and the electron’s mass. Only two electrons, one spin up and one spin down, can occupy each of these energy levels owing to the Pauli exclusion principle, while other electrons must occupy higher, more voluminous orbitals. When you drop from a higher energy level to a lower one, you must change the type of orbital you’re in if you’re only going to emit one photon, otherwise you’ll violate certain conservation laws that cannot be broken.

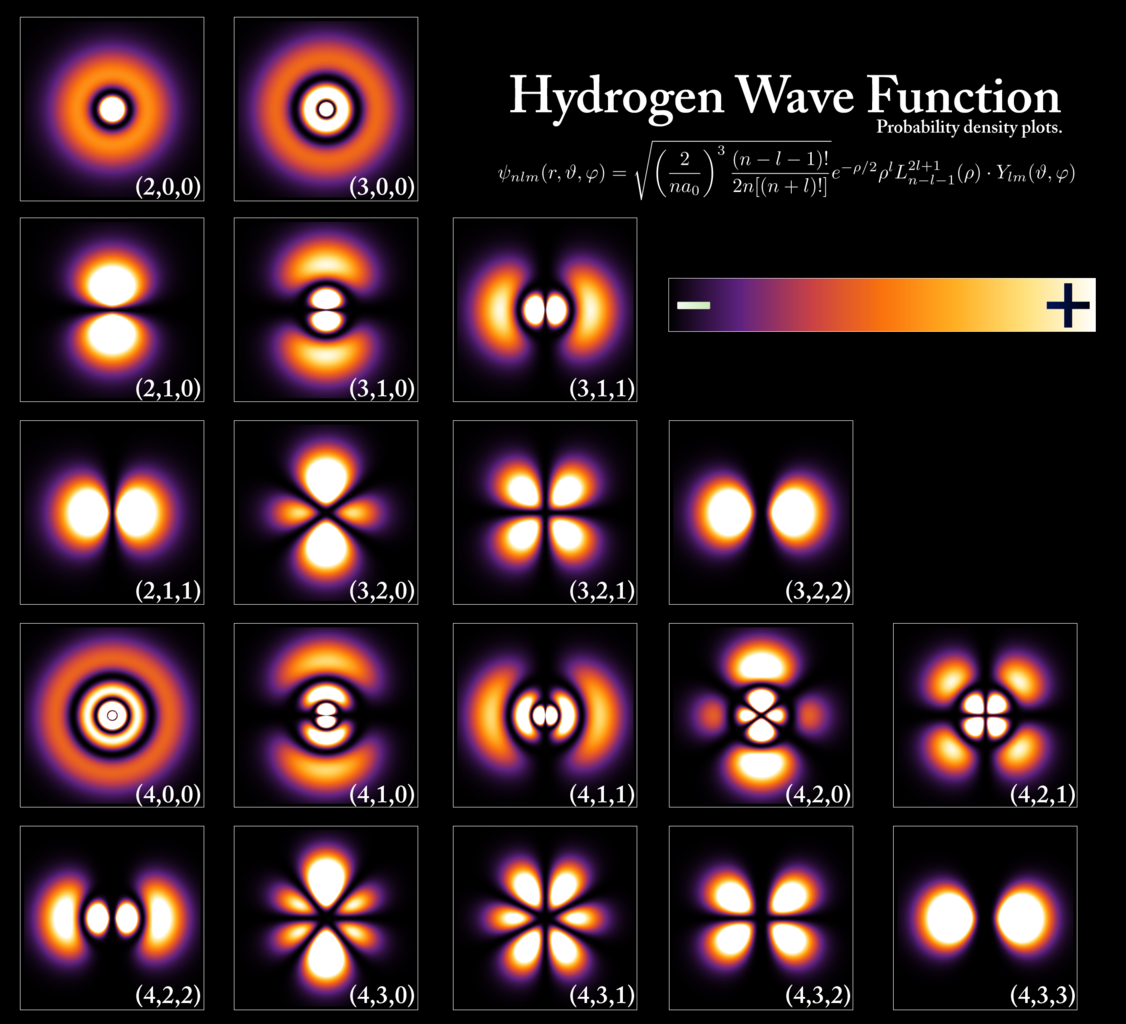
That’s because the Universe has a trick up its sleeve: making an “impossible” quantum transition happen.

You’ll recall that there are not only different energy levels within atoms, but different orbitals within energy levels as well.

• The lowest energy level can only hold 2 electrons, and has only (spherical) s-orbitals.
• The second energy level can hold up to 8 electrons, having s-orbitals and also (perpendicular) p-orbitals.
• The third energy level holds up to 18 electrons, with s-orbitals, p-orbitals, and d-orbitals.

And so on. But you can’t just transition from any higher-energy level to any lower-energy level. There’s a quantum restriction because of conservation laws, and the restriction is this: if you’re going to emit a (spin-1) photon, your electron needs to jump from an orbital in one energy level to a different orbital at a lower energy level. If you’re in a 2p orbital, you’re all set: jumping down to the 1s orbital is no problem. But if you’re in the 2s orbital, you’re stuck! You can’t go down to the 1s orbital, because that would violate our quantum rules.

Or are you?

It turns out that from any higher-energy s-orbital, you can transition down to the 1s-orbital (the ground state) by emitting two photons instead of one by taking advantage of a “virtual” transition to a higher-energy p-orbital or d-orbital. Remember that in quantum mechanics, there’s a small but non-zero probability of occupying energetically forbidden states, enabling you to quantum tunnel into the ground state. In the case of transitioning down to the ground state of hydrogen, it means that on rare occasion — about once per 100,000,000 transitions — instead of emitting a Lyman-series photon when you reach the ground state, you instead emit two photons of only half the required energy.

When you transition from an “s” orbital to a lower-energy “s” orbital, you can on rare occasion do it through the emission of two photons of equal energy. This two-photon transition occurs even between the 2s (first excited) state and the 1s (ground) state, about one time out of every 100 million transitions, and is the primary mechanism by which the Universe’s atoms become neutral.

This time, there is no “reverse reaction,” as absorbing two photons simultaneously will not occur, and there’s no “intermediate state” where only one photon is absorbed: it’s a “both or none” situation. Whenever this two-photon transition occurs, you always wind up making one extra neutral hydrogen atom over what you started with. Even though it’s a forbidden quantum process, and even though it only occurs rarely, this actually represents the dominant way that the majority of atoms in the Universe finally become neutral.

If there were no atoms at all, it would take over a billion years to have the Universe become transparent to light. If it weren’t for the quantum mechanical possibility of having a two-photon transition, it would have taken nearly a million years for the Universe to become transparent to form neutral atoms and become transparent to light. But with the actual laws of quantum mechanics and a Universe that expanded and cooled since the hot Big Bang, it’s only a mere 380,000 years until practically all of the atoms within it are neutral and stable, and the (now-infrared) light present within it can simply stream freely through space. It sets the stage for the formation of the first stars, and once gravitation, nuclear fusion, and time all do their things, planets, life, and complex organisms can arise, reconstructing what happened all those billions of years before!