Why we need quantum fields, not just quantum particles

- One of the most revolutionary discoveries of the 20th century is that certain properties of the Universe are quantized and obey counterintuitive quantum rules.
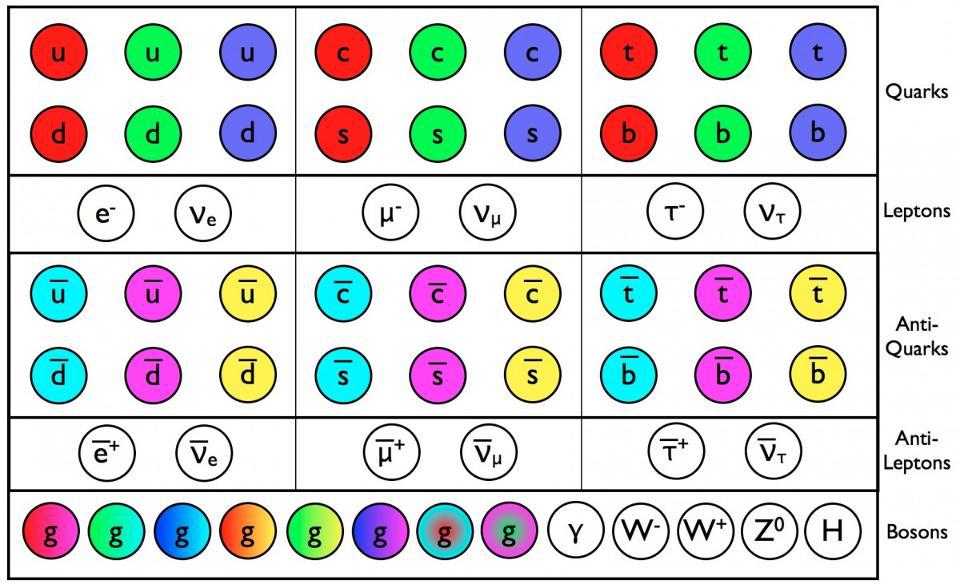
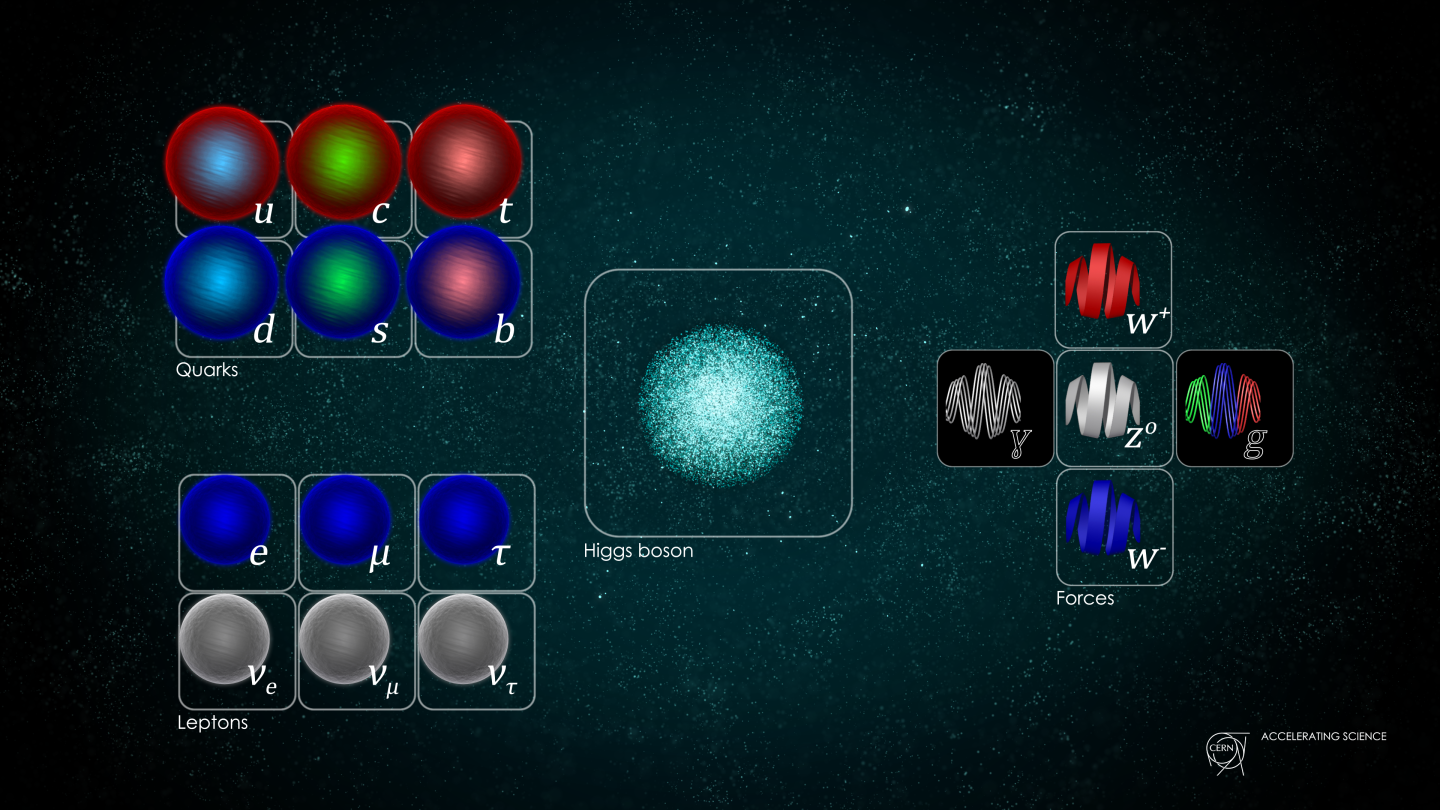
- The fundamental constituents of matter are quantized into discrete, individual particles, which exhibit weird and “spooky” behaviors that surprise us constantly.
- But the Universe’s quantum weirdness goes even deeper: down to the fields that permeate all of space, with or without particles. Here’s why we need them, too.
Of all the revolutionary ideas that science has entertained, perhaps the most bizarre and counterintuitive one is the notion of quantum mechanics. Previously, scientists had assumed that the Universe was deterministic, in the sense that the laws of physics would enable you to predict with perfect accuracy how any system would evolve into the future. We assumed that our reductionist approach to the Universe — where we searched for the smallest constituents of reality and worked to understand their properties — would lead us to the ultimate knowledge of things. If we could know what things were made of and could determine the rules that governed them, nothing, at least in principle, would be beyond our ability to predict.
This assumption was quickly shown not to be true when it comes to the quantum Universe. When you reduce what’s real to its smallest components, you find that you can divide all forms of matter and energy into indivisible parts: quanta. However, these quanta no longer behave in a deterministic fashion, but only in a probabilistic one. Even with that addition, however, another problem still remains: the effects that these quanta cause on one another. Our classical notions of fields and forces fail to capture the real effects of the quantum mechanical Universe, demonstrating the need for them to be somehow quantized, too. Quantum mechanics isn’t sufficient to explain the Universe; for that, quantum field theory is needed. This is why.
It’s possible to imagine a Universe where nothing at all was quantum, and where there was no need for anything beyond the physics of the mid-to-late 19th century. You could divide matter into smaller and smaller chunks as much as you like, with no limit. At no point would you ever encounter a fundamental, indivisible building block; you could reduce matter down into arbitrarily small pieces, and if you had a sharp or strong enough “divider” at your disposal, you could always break it down even further.
In the early 20th century, however, this idea was shown to be incompatible with reality. Radiation from heated objects doesn’t get emitted at all frequencies, but rather is quantized into individual “packets” each containing a specific amount of energy. Electrons can only be ionized by light whose wavelength is shorter (or frequency is higher) than a certain threshold. And particles emitted in radioactive decays, when fired at a thin piece of gold foil, would occasionally ricochet back in the opposite direction, as though there were hard “chunks” of matter in there that those particles couldn’t pass through.
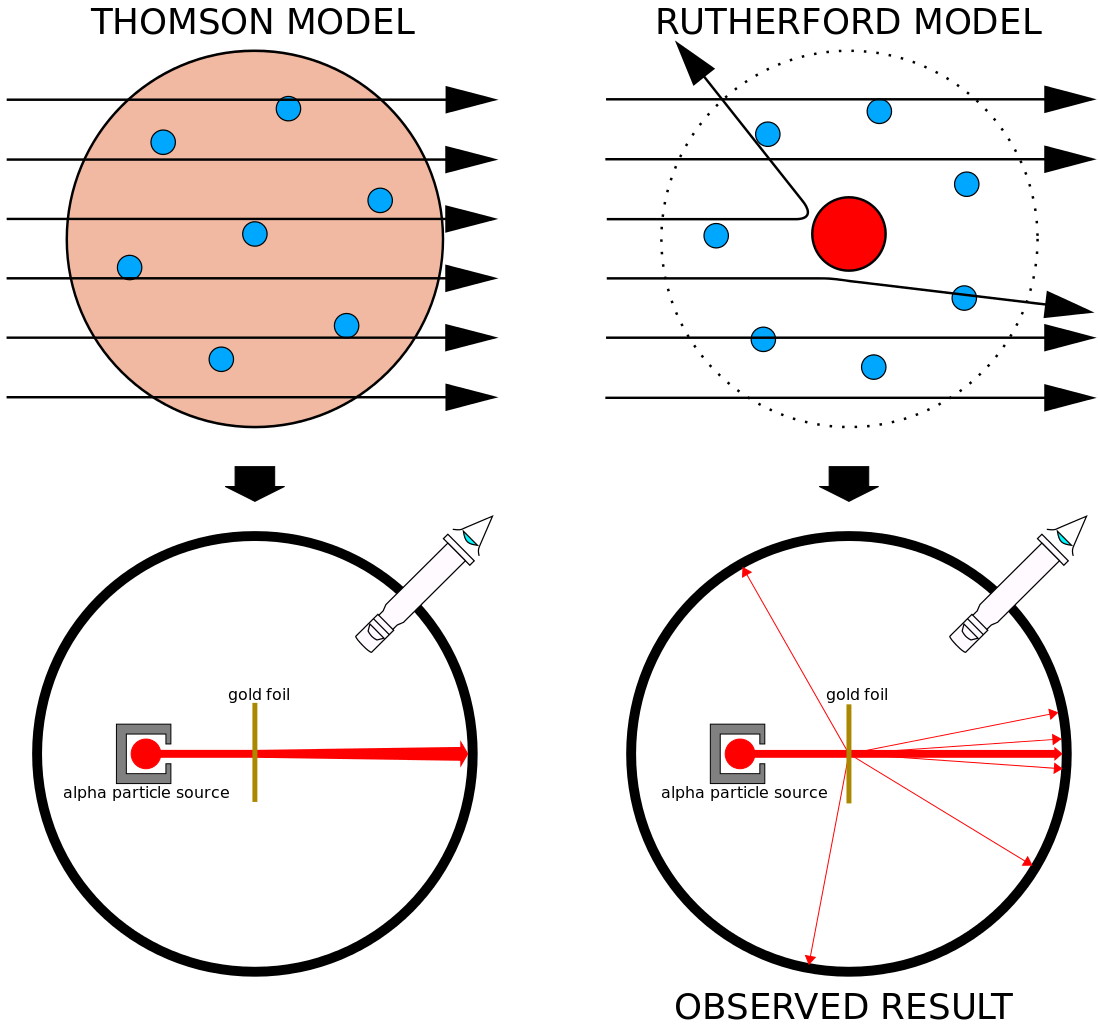
The overwhelming conclusion was that matter and energy couldn’t be continuous, but rather were divisible into discrete entities: quanta. The original idea of quantum physics was born with this realization that the Universe couldn’t be entirely classical, but rather could be reduced into indivisible bits which appeared to play by their own, sometimes bizarre, rules. The more we experimented, the more of this unusual behavior we uncovered, including:
- the fact that atoms could only absorb or emit light at certain frequencies, teaching us that energy levels were quantized,
- that a quantum fired through a double slit would exhibit wave-like, rather than particle-like, behavior,
- that there’s an inherent uncertainty relation between certain physical quantities, and measuring one more precisely increases the inherent uncertainty in the other,
- and that outcomes were not deterministically predictable, but that only probability distributions of outcomes could be predicted.
These discoveries didn’t just pose philosophical problems but physical ones as well. For example, there’s an inherent uncertainty relationship between the position and the momentum of any quantum of matter or energy. The better you measure one, the more inherently uncertain the other one becomes. In other words, positions and momenta can’t be considered to be solely a physical property of matter, but they must be treated as quantum mechanical operators, yielding only a probability distribution of outcomes.

Why would this be a problem?
Because these two quantities, measurable at any instant in time that we so choose, have a time-dependence. The positions that you measure or the momenta that you infer a particle possesses will change and evolve with time.
That would be fine on its own, but then there’s another concept that comes to us from special relativity: the notion of time is different for different observers, so the laws of physics that we apply to systems must remain relativistically invariant. After all, the laws of physics shouldn’t change just because you’re moving at a different speed, in a different direction, or are at a different location from where you were before.
As originally formulated, quantum physics was not a relativistically invariant theory; its predictions were different for different observers. It took years of developments before the first relativistically invariant version of quantum mechanics was discovered, which didn’t happen until the late 1920s.
If we thought the predictions of the original quantum physics were weird, with their indeterminism and fundamental uncertainties, a whole slew of novel predictions emerged from this relativistically invariant version. They included:
- an intrinsic amount of angular momentum inherent to quanta, known as spin,
- magnetic moments for these quanta,
- fine-structure properties,
- novel predictions about the behavior of charged particles in the presence of electric and magnetic fields,
- and even the existence of negative energy states, which were a puzzle at the time.
Later on, those negative energy states were identified with an “equal-and-opposite” set of quanta that were shown to exist: antimatter counterparts to the known particles. It was a great leap forward to have a relativistic equation that described the earliest known fundamental particles, such as the electron, positron, muon, and more.
However, it couldn’t explain everything. Radioactive decay was still a mystery. The photon had the wrong particle properties, and this theory could explain electron-electron interactions but not photon-photon interactions. Clearly, a major component of the story was still missing.
Here’s one way to think about it: imagine an electron traveling through a double slit. If you don’t measure which slit the electron goes through — and for these purposes, assume that we don’t — it behaves as a wave: part of it goes through both slits, and those two components interfere to produce a wave pattern. The electron is somehow interfering with itself along its journey, and we see the results of that interference when we detect the electrons at the end of the experiment. Even if we send those electrons one-at-a-time through the double slit, that interference property remains; it’s inherent to the quantum mechanical nature of this physical system.
Now ask yourself a question about that electron: what happens to its electric field as it goes through the slits?
Previously, quantum mechanics had replaced our notions of quantities like the position and momentum of particles — which had been simply quantities with values — with what we call quantum mechanical operators. These mathematical functions “operate” on quantum wavefunctions, and produce a probabilistic set of outcomes for what you might observe. When you make an observation, which really just means when you cause that quantum to interact with another quantum whose effects you then detect, you only recover a single value.
But what do you do when you have a quantum that’s generating a field, and that quantum itself is behaving as a decentralized, non-localized wave? This is a very different scenario than what we’ve considered in either classical physics or in quantum physics so far. You can’t simply treat the electric field generated by this wave-like, spread-out electron as coming from a single point, and obeying the classical laws of Maxwell’s equations. If you were to put another charged particle down, such as a second electron, it would have to respond to whatever weird sort of quantum-behavior this quantum wave was causing.
Normally, in our older, classical treatment, fields push on particles that are located at certain positions and change each particle’s momentum. But if the particle’s position and momentum are inherently uncertain, and if the particle(s) that generate the fields are themselves uncertain in position and momentum, then the fields themselves cannot be treated in this fashion: as though they’re some sort of static “background” that the quantum effects of the other particles are superimposed atop.
If we do, we’re short-changing ourselves, inherently missing out on the “quantum-ness” of the underlying fields.

This was the enormous advance of quantum field theory, which didn’t just promote certain physical properties to being quantum operators, but promoted the fields themselves to being quantum operators. (This is also where the idea of second quantization comes from: because not just the matter and energy are quantized, but the fields as well.) All of a sudden, treating the fields as quantum mechanical operators enabled an enormous number of phenomena that had already been observed to finally be explained, including:
- particle-antiparticle creation and annihilation,
- radioactive decays,
- quantum tunneling resulting in the creation of electron-positron pairs,
- and quantum corrections to the electron’s magnetic moment.
With quantum field theory, all of these phenomena now made sense, and many other related ones could now be predicted, including the very exciting modern disagreement between the experimental results for the muon’s magnetic moment and two different theoretical methods of calculating it: a non-perturbative one, which agrees with experiment, and a perturbative one, which doesn’t.

One of the key things that comes along with quantum field theory that simply wouldn’t exist in normal quantum mechanics is the potential to have field-field interactions, not just particle-particle or particle-field interactions. Most of us can accept that particles will interact with other particles, because we’re used to two things colliding with one another: a ball smashing against a wall is a particle-particle interaction. Most of us can also accept that particles and fields interact, like when you move a magnet close to a metallic object, the field attracts the metal.
Although it might defy your intuition, the quantum Universe doesn’t really pay any mind to what our experience of the macroscopic Universe is. It’s much less intuitive to think about field-field interactions, but physically, they’re just as important. Without it, you couldn’t have:
- photon-photon collisions, which are a vital part of creating matter-antimatter pairs,
- gluon-gluon collisions, which are responsible for the majority of high-energy events at the Large Hadron Collider,
- and having both neutrinoless double beta decay and double-neutrino double beta decay, the latter of which has been observed and the former of which is still being searched for.

The Universe, at a fundamental level, isn’t just made of quantized packets of matter and energy, but the fields that permeate the Universe are inherently quantum as well. It’s why practically every physicist fully expects that, at some level, gravitation must be quantized as well. General Relativity, our current theory of gravity, functions in the same way that an old-style classical field does: it curves the backdrop of space, and then quantum interactions occur in that curved space. Without a quantized gravitational field, however, we can be certain we’re overlooking quantum gravitational effects that ought to exist, even if we aren’t certain of what all of them are.
In the end, we’ve learned that quantum mechanics is fundamentally flawed on its own. That’s not because of anything weird or spooky that it brought along with it, but because it wasn’t quite weird enough to account for the physical phenomena that actually occur in reality. Particles do indeed have inherently quantum properties, but so do fields: all of them relativistically invariant. Even without a current quantum theory of gravity, it’s all but certain that every aspect of the Universe, particles and fields alike, are themselves quantum in nature. What that means for reality, exactly, is something we’re still trying to puzzle out.