The surprising quantum reason why the Sun shines

Earth, as we know it, is only teeming with life because of the influence of our Sun. Its light and heat provides every square meter of Earth — when it’s in direct sunlight — with a constant ~1500 W of power, enough to keep our planet at a comfortable temperature for liquid water to continuously exist on its surface. Just like the hundreds of billions of stars in our galaxy amidst the trillions of galaxies in the Universe, our Sun shines continuously, varying only slightly over time.

But without quantum physics, the Sun wouldn’t shine at all. Even in the extreme conditions found in the core of a massive star like our Sun, the nuclear reactions that power it could not occur without the bizarre properties that our quantum Universe demands. Thankfully, our Universe is quantum in nature, enabling the Sun and all the other stars to shine as they do. Here’s the science of how it works.

This glimpse into the stars found in the densest region of the Orion Nebula, near the heart of the Trapezium Cluster, shows a modern glimpse inside a star-forming region of the Milky Way. However, star-formation properties vary over cosmic time, from galaxy to galaxy, at different radii from the galactic center, etc. All of these properties and more must be reckoned with to compare the Sun with the overall population of stars within the Universe.

Starlight is the single greatest source of energy in the Universe throughout its entire 13.8 billion year history, subsequent to the hot Big Bang. These large, massive concentrations of hydrogen and helium contract under their own gravity when they first form, causing their cores to become denser and denser all while heating up. Eventually, a critical threshold is reached — at temperatures of ~4 million kelvin and densities exceeding that of solid lead — where nuclear fusion begins in the star’s core.

But here’s the puzzle: you can determine exactly how much energy the particles in the Sun must have, and calculate how those energies are distributed. You can calculate what types of collisions occur between protons in the Sun’s core, and compare that with how much energy is required to actually bring two protons into physical contact with one another: overcoming the electric repulsion between them.

And when you do your calculations, you find a shocking conclusion: there are zero collisions happening there with enough energy to lead to nuclear fusion. Zero. None at all.

A solar flare from our Sun, which ejects matter out away from our parent star and into the Solar System, is dwarfed in terms of ‘mass loss’ by nuclear fusion, which has reduced the Sun’s mass by a total of 0.03% of its starting value: a loss equivalent to the mass of Saturn. E=mc², when you think about it, showcases how energetic this is, as the mass of Saturn multiplied by the speed of light (a large constant) squared leads to a tremendous amount of energy produced.

At first glance, this would appear to make nuclear fusion — and hence, the ability of the Sun to shine — completely impossible. And yet, based on the energy we observe coming from the Sun, we know that it does, in fact, shine.

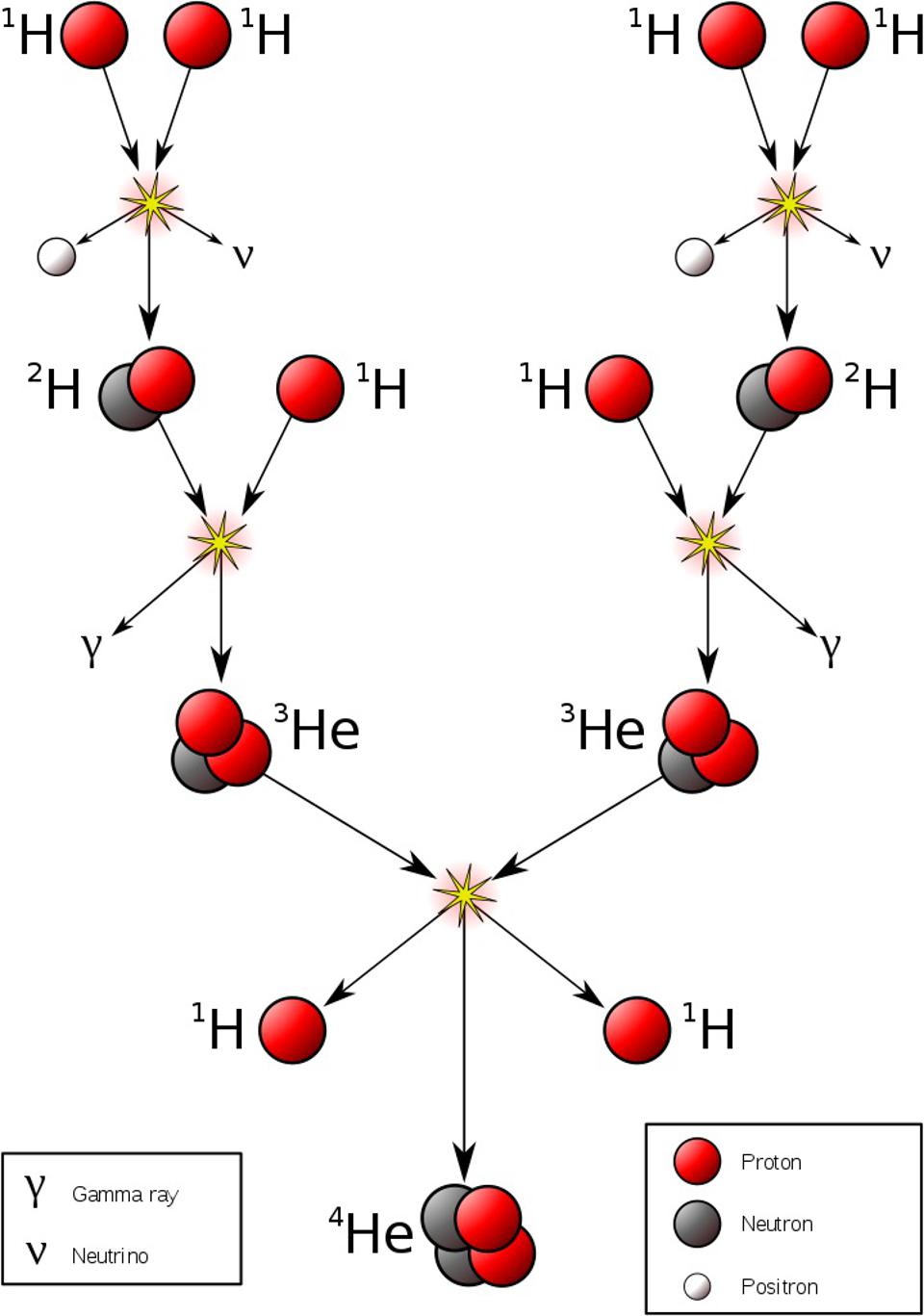
Deep inside the Sun, in the innermost regions where the temperature ranges between 4 million all the way up to 15 million kelvin, the nucleus of four initial hydrogen atoms (i.e., individual protons) will fuse together in a chain reaction, with the end result producing a helium nucleus (made of two protons and two neutrons), along with the release of a significant amount of energy.

That energy is carried away in the form of both neutrinos and photons, and while the photons might spend over 100,000 years before they make it to the Sun’s photosphere and radiate into space, the neutrinos exit the Sun in mere seconds, where we’ve been detecting them on Earth since the 1960s.

Experiments such as Super-Kamiokande, which contain enormous tanks of (proton-rich) water surrounded by arrays of detectors, are the most sensitive tools humanity has to detect neutrinos from the Sun. Compared to the number of electron neutrinos we naively expected to appear in the detector, the measured signal is only about one-third of the predicted value.

You might think about this scenario and be a bit puzzled, since it isn’t obvious how energy is released from these reactions. Neutrons, you see, are ever so slightly more massive than protons are: by about 0.1%. When you fuse four protons into a nucleus containing two protons and two neutrons, you might think that reaction would require energy instead of emitting it.

If all of those particles were free and unbound, that would be true. But when neutrons and protons are bound together into a nucleus such as helium, they wind up being bound together so tightly that they’re actually significantly less massive than their individual, unbound constituents. While two neutrons have about 2 MeV (where an MeV is one million electron-volts, a measure of energy) more energy than two protons are — via Einstein’s E = mc² — a helium nucleus is the equivalent of 28 MeV lighter than four unbound protons.

In other words, the process of nuclear fusion releases energy: about 0.7% of whatever protons fuse together gets converted into energy, carried by both neutrinos and photons.

The most straightforward and lowest-energy version of the proton-proton chain, which produces helium-4 from initial hydrogen fuel. Note that only the fusion of deuterium and a proton produces helium from hydrogen; all other reactions either produce hydrogen or make helium from other isotopes of helium.

We observe the Sun emitting, over its entire surface, a continuous power output of 4 × 10²⁶ Watts. That amount of energy translates into an enormous number of protons — somewhere upward of 10³⁸ of them — fusing together in this chain reaction every second. This is spread out over an enormous volume of space, of course, since the interior of the Sun is enormous; the average human being metabolizing their daily food produces more energy than an equivalent human-sized volume of the Sun.

But with all of those reactions occurring in the interior of the Sun, you might start to wonder how efficient these reactions are. Do we really get enough of them to generate all the power that the Sun creates? Can this really lead to such an enormous energy output, and explain how the Sun shines?

It’s a complex question, and if you start to think about it quantitatively, here are the numbers you arrive at.

The anatomy of the Sun, including the inner core, which is the only place where fusion occurs. Even at the incredible temperatures of 15 million K, the maximum achieved in the Sun, the Sun produces less energy-per-unit-volume than a typical human body. The Sun’s volume, however, is large enough to contain over 1⁰²⁸ full-grown humans, which is why even a low rate of energy production can lead to such an astronomical total energy output.

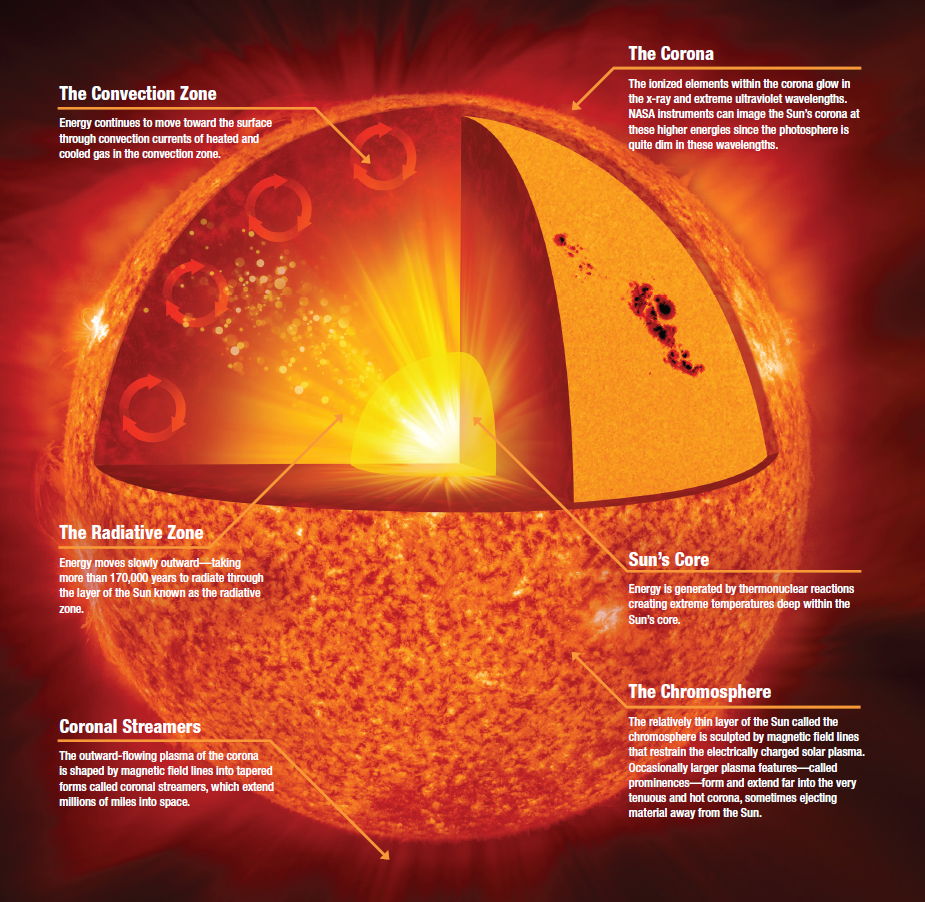
The Sun is far larger and more massive than anything we’ve experienced in our lives. If you were to take the entire planet Earth and line up a series of them across the Sun’s diameter, it would take 109 Earths to make it all the way across. If you were to take all the mass contained within planet Earth, you’d have to accumulate more than 300,000 of them to equal the mass of our Sun.

All told, there are some 10⁵⁷ particles making up the Sun, with right around 10% of those particles present in the fusion region that defines the Sun’s core. Inside the core, here’s what’s happening:

• Individual protons reach tremendous speeds, up to ~500 km/s in the Sun’s central core, where temperatures reach up to 15 million K.
• These fast-moving particles are so numerous that each proton experiences billions of collisions each second.
• And only a tiny fraction of these collisions need to create deuterium — just 1 in 10²⁸ — in a fusion reaction to produce the needed energy.

This cutaway showcases the various regions of the surface and interior of the Sun, including the core, which is the only location where nuclear fusion occurs. As time goes on and hydrogen is consumed, the helium-containing region in the core expands and the maximum temperature increases, causing the Sun’s energy output to increase.

This sounds reasonable, right? Surely, given the enormous number of proton collisions that occur, how fast they’re moving, and the fact that only a tiny, almost imperceptible fraction of them would need to actually fuse, this could be achievable.

So we do the math. We calculate, based on how particles behave and move when you have a whole lot of them under a given set of energies and velocities, how many proton-proton collisions have enough energy to initiate nuclear fusion in those reactions.

To get there, all two protons have to do is get close enough to physically touch, overcoming the fact that they both have positive electric charges, and that like charges repel.

So how many of the ~10⁵⁶ protons in the Sun’s core, colliding billions of times per second, actually have enough energy to cause a fusion reaction to occur?

Exactly zero.

When two protons overlap, it’s possible that they can fuse together into a composite state dependent on their properties. The most common, stable possibility is to produce a deuteron, made of a proton and a neutron, which requires the emission of a neutrino, a positron, and possibly a photon as well.

And yet, somehow, it happens. Not only does nuclear fusion successfully power the Sun, but stars far less massive — and with far lower core temperatures — than our own. Hydrogen gets converted to helium; fusion occurs; starlight gets created; planets become potentially habitable.

So what’s the secret?

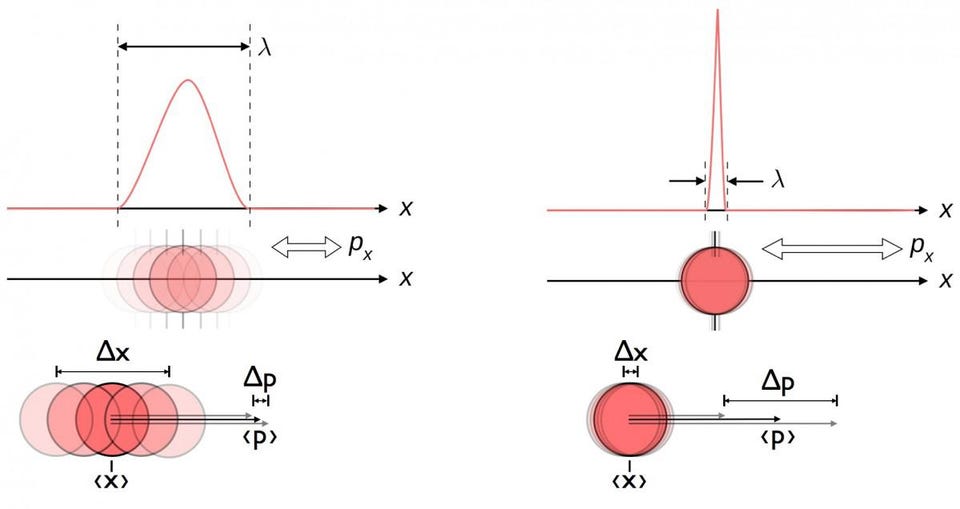
This is the key place where quantum physics comes into play. Down at a subatomic level, atomic nuclei don’t actually behave as particles alone, but rather as waves. Sure, you can measure the physical size of a proton, but doing so makes its momentum inherently uncertain. You can also measure the momentum of a proton — essentially what we did when we calculated what its velocity is — but doing so makes its position more inherently uncertain.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Each proton, instead, is a quantum particle, where its physical location is better described by a probability function than a pinned-down position.

This diagram illustrates the inherent uncertainty relation between position and momentum. When one is known more accurately, the other is inherently less able to be known accurately. Other pairs of conjugate variables, including energy and time, spin in two perpendicular directions, or angular position and angular momentum, also exhibit this same uncertainty relation.

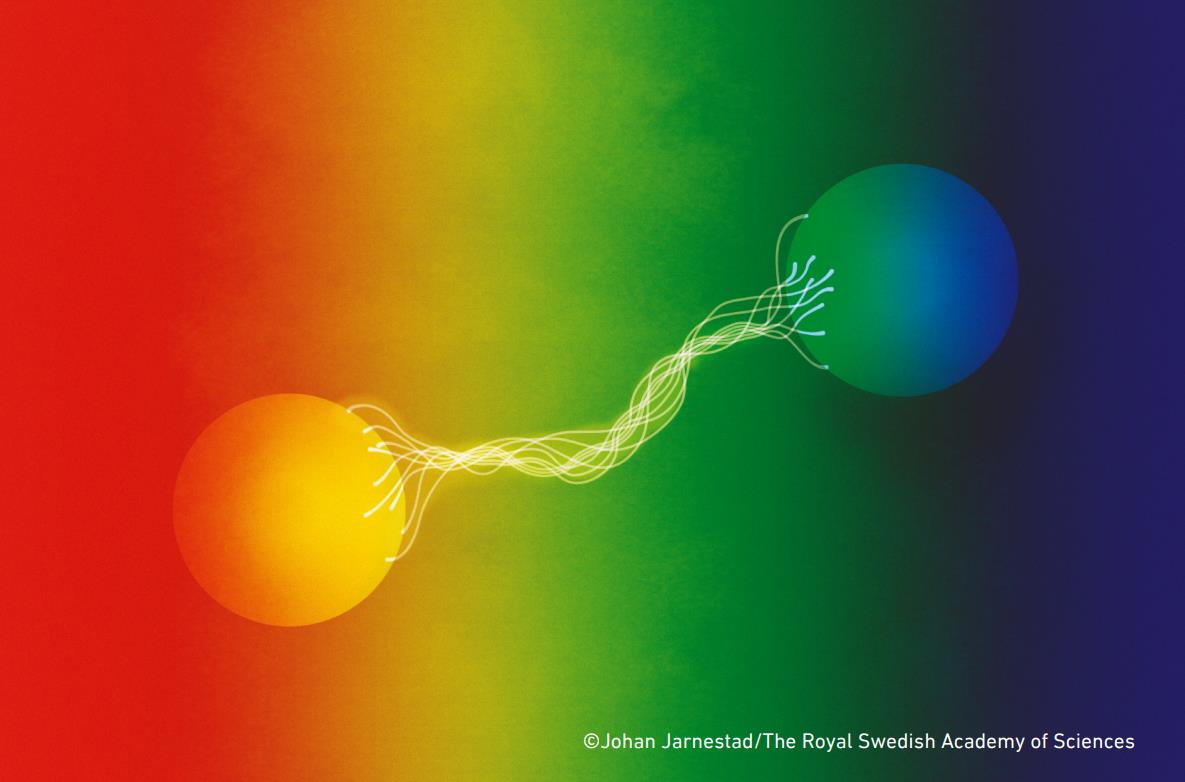
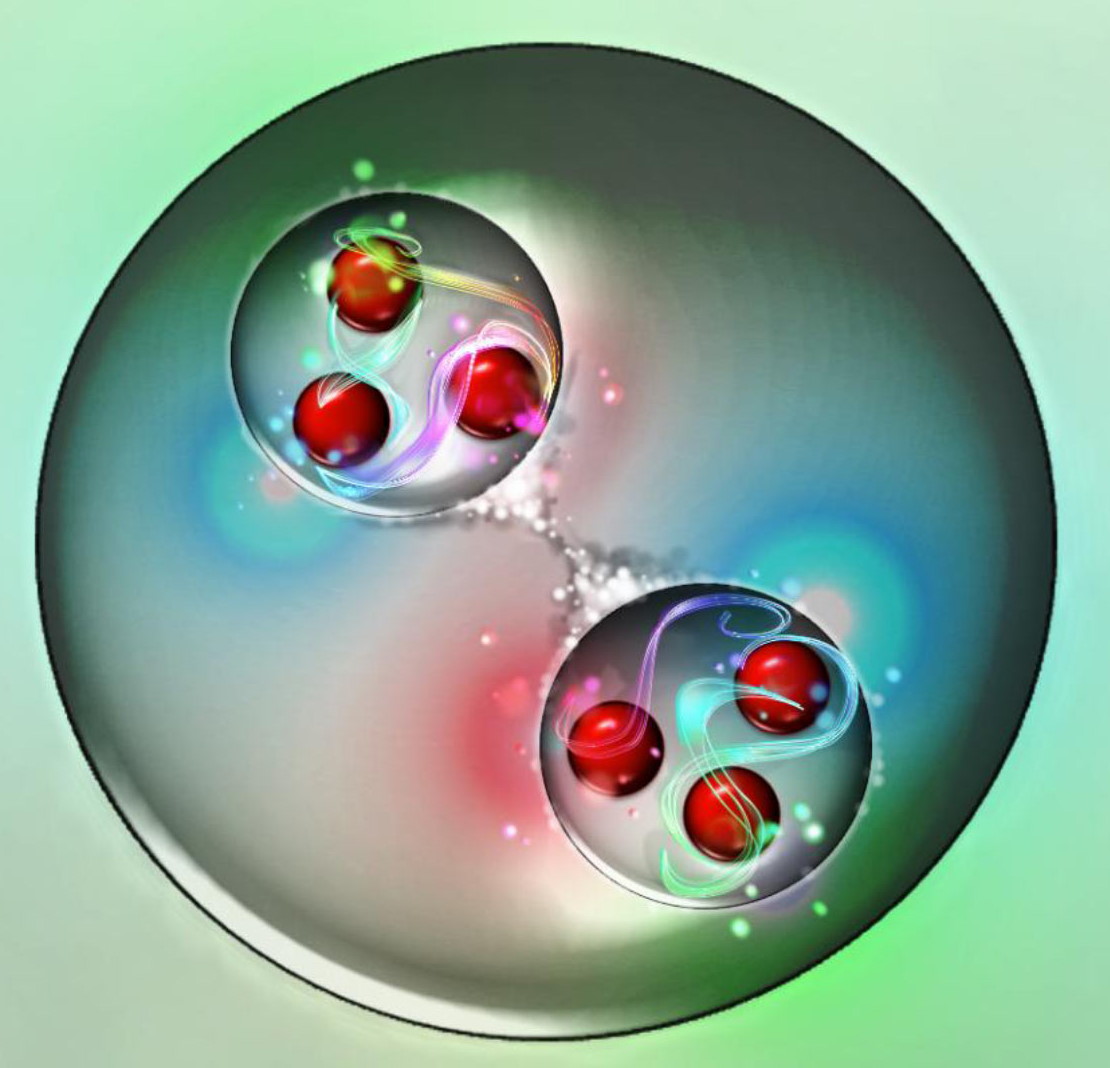
Because of the quantum nature of these protons, the wavefunctions of two protons can overlap. Even protons which don’t have enough energy to overcome the repulsive electric force between them can see their wavefunctions overlap, and that overlapping means they have a finite probability of experiencing quantum tunneling: where they can end up in a more stable bound state than their initial, free state.

Once you form deuterium from two protons — the hard part — the rest of the chain reaction can proceed quite quickly, leading to the formation of helium-4 in short order.

But the probability of forming deuterium is very small. In fact, for any particular proton-proton interaction that occurs in the Sun’s core, practically all of them will have the simplest result imaginable: their wavefunctions temporarily overlap, then they stop overlapping, and all you wind up with is two protons, the same as what you started with. But a very small fraction of the time, about 1 in every 10²⁸ collisions (remember that number from earlier?), two protons wind up fusing together, creating a deuteron, as well as a positron and a neutrino, and possibly also a photon.

When two protons meet each other in the Sun, their wavefunctions overlap, allowing the temporary creation of helium-2: a diproton. Almost always, it simply splits back into two protons, but on very rare occasions, a stable deuteron (hydrogen-2) is produced, due to both quantum tunneling and the weak interaction.

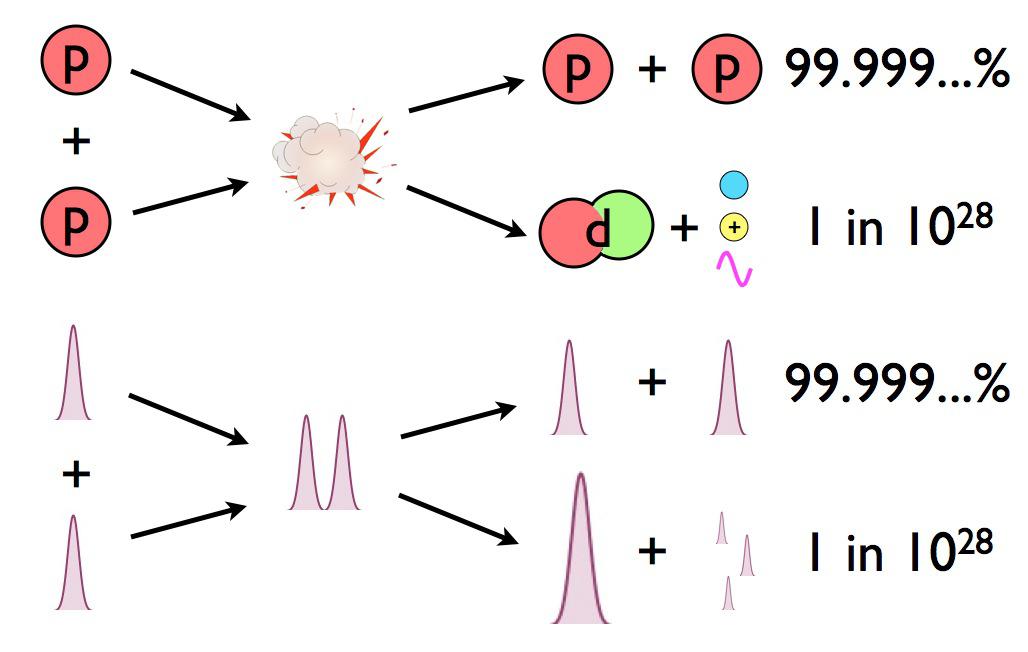
When the wavefunction of two protons in the Sun’s core overlap, there’s only a minuscule chance that they’ll do anything other than return to being two protons. The odds of them fusing together to make a deuterium nucleus are about the same as winning the Powerball lottery three times in a row: astronomically small. And yet, there are so many protons inside the Sun that this successfully occurs so often that it powers not only our Sun, but practically all of the stars in the Universe.

Over the past 4.5 billion years, this has happened enough times in our Sun that it has lost approximately the mass of Saturn due to nuclear fusion and Einstein’s most famous equation: E = mc². If it weren’t for the quantum nature of the Universe, however, nuclear fusion wouldn’t occur in the Sun at all, and Earth would simply be a cold, lifeless rock floating in the abyss of space. It’s only because of the uncertainty inherent to position, momentum, energy, and time, that our existence is possible at all. Without quantum physics, the Sun wouldn’t be able to shine. In a very real sense, we really did win the cosmic lottery.