Ask Ethan: How does dark energy accelerate the Universe?

It’s all too easy to accept what we know — or think we know — without examining it too critically. But when it comes to the great mysteries of our cosmic reality, that close, critical examination is exactly what’s required to help us truly, deeply understand what’s at play. At first pass, the expanding Universe might seem like an easy thing to accept: some sort of rapid, initial expansion started off our Universe, while the gravitational effects of all the matter and energy within it work to bring things back together. If gravitation won, we’d end in a Big Crunch; if the expansion won, we’d end in a Big Freeze.

Only, when we examined our Universe in sufficient detail, we found that not only is the expansion going to win, but that distant objects are actually speeding up as they recede from us. Somehow, they’re moving away faster and faster as time goes on. How do we make sense of this? That’s what Patreon supporter Bob Schier wants to know, asking:

“How does dark energy produce increasing acceleration.. away from itself? Is it a kind of ‘negative gravity’ in which matter repels matter similar to the way that like charges repel each other? Or does it stretch the ‘fabric of space-time’ or simply of space?”

There are many ways to conceptualize the expanding Universe and dark energy, but “repulsion” isn’t one of them. Let’s start at the beginning: with the concept of cosmic expansion.

This simplified animation shows how light redshifts and how distances between unbound objects change over time in the expanding Universe. Note that the objects start off closer than the amount of time it takes light to travel between them, the light redshifts due to the expansion of space, and the two galaxies wind up much farther apart than the light-travel path taken by the photon exchanged between them.

When Einstein first put forth his new theory of gravitation to replace Newtonian gravity, his theory of General Relativity, it was a radical way of viewing the Universe. Instead of viewing space and time as independent, absolute entities — where space is a static, three-dimensional grid and time is simply an inexorable, forward-moving line — three great advances came along, hand-in-hand, in the early 20th century.

1. First, there was the notion that arrived with Special Relativity in 1905: that neither space nor time were absolutes, but that they were only experienced relative to the observer. Whenever two observers were either at different locations or had different motions through space, they experienced space and time differently from one another.
2. Second, there was a way to “weave” space and time together: discovered by Einstein’s former teacher, Hermann Minkowski, in 1908. This fabric, spacetime, would replace the independent notions of space and time, individually.
3. And third, there was the notion that gravitation could be included in the spacetime picture as well, where matter-and-energy curved the fabric of spacetime, and that curved spacetime told matter and energy how to move.

An animated look at how spacetime responds as a mass moves through it helps showcase exactly how, qualitatively, it isn’t merely a sheet of fabric. Instead, all of 3D space itself gets curved by the presence and properties of the matter and energy within the Universe. Multiple masses in orbit around one another will cause the emission of gravitational waves.

But here was the kicker: if matter and energy curved the fabric of spacetime, then that implied the fabric wouldn’t be static, but would change over time. Most of us think of curvature as having three possibilities, where you could be curved positively, like a sphere, or you could be curved negatively, like a Pringles’ chip or a horse’s saddle, or you could have zero curvature, being flat like a sheet of paper. Those three examples are all true: curvature could mean any of those three things.

But curvature could also lead to something else entirely: expansion or contraction.

One of Einstein’s first thought experiments in the context of General Relativity was to imagine what would happen if you had a Universe — i.e., a spacetime — that was uniformly filled with what he thought of as dust: massive particles, evenly distributed, at rest with respect to one another and to the backdrop of spacetime. When you calculate what happens in the context of General Relativity, you find that space curves in such a way that these dust particles all get closer and closer, with the distance between them decreasing, until they all meet at a single point. It seemed inevitable that what you’d get was the solution that Karl Schwarzschild derived just months after General Relativity was put forth in its final form: a black hole.

In a Universe that isn’t expanding, you can fill it with stationary matter in any configuration you like, but it will always collapse down to a black hole. Such a Universe is unstable in the context of Einstein’s gravity, and must be expanding to be stable, or we must accept its inevitable fate.

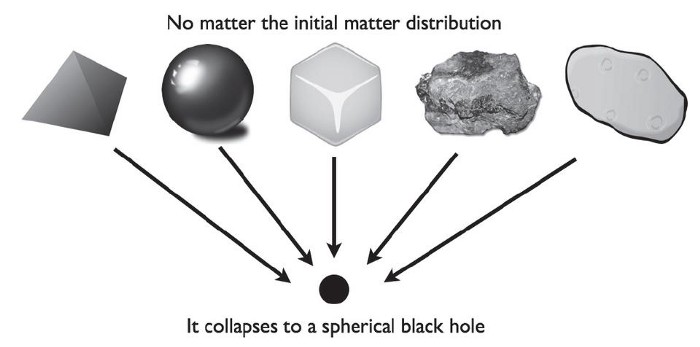
Einstein went further than this, and realized that it didn’t matter what the extent of the matter distribution was, nor did the geometry matter. Whether the matter was distributed in a sphere, a cube, a pyramid, a potato-like structure, or any geometrical shape, it didn’t matter: you’d still collapse down to a black hole.

But it wasn’t simply because spacetime curved in such a way that it caused the matter to move through space and accelerate into a single point; as intuitive as that explanation is, it doesn’t accurately depict what’s going on.

Instead, what’s happening is that spacetime curves in such a way that the fabric itself actually “flows” inward into itself, so that the entire fabric — or, at least, the fabric within this region of space — contracts. It’s as though there’s an invisible, omnidirectional “moving walkway” that drags these particles inward. Even if space were absolutely infinite, and it was infinitely filled with this dust everywhere, the entire fabric of spacetime would get pulled inward, as though it were contracting. If this situation did encapsulate the entire Universe, it would end in a singularity: a “point” where all of spacetime reached arbitrary, infinite density. If this scenario only applied to a finite region of the Universe, you’d get a black hole, where this “moving walkway” analogy continued to draw not just matter, but spacetime, into it.

Both inside and outside the event horizon of a Schwarzschild black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. At the event horizon, even if you ran (or swam) at the speed of light, there would be no overcoming the flow of spacetime, which drags you into the singularity at the center. Outside the event horizon, though, other forces (like electromagnetism) can frequently overcome the pull of gravity, causing even infalling matter to escape. This spacetime conserves energy, as it’s time-translation invariant.

It was still in the very early days of General Relativity that Einstein realized this pathology: we lived in a Universe that was filled with matter. But if your Universe is filled with matter, it won’t remain static and stable; the fabric of spacetime will collapse inward on itself, leading to a Big Crunch scenario in short order. Therefore — in a move that Einstein would later tout as his “biggest blunder” — Einstein realized that another form of energy must be “holding the Universe up against gravitational collapse,” so he introduced what we know today as either a cosmological constant or as dark energy: the only way he could think of to balance out this otherwise inevitable gravitational collapse.

This brings us to the big question: how does “dark energy” actually do this? How does it prevent the Universe from collapsing? How does it resist the gravitational attraction of matter and other forms of energy? And, after all, if dark energy is just another form of energy, wouldn’t it also cause the Universe to gravitate, leading to gravitational collapse anyway?

In order to answer this, we have to get quantitative.

A photo of Ethan Siegel at the American Astronomical Society’s hyperwall in 2017, along with the first Friedmann equation at right. The first Friedmann equation details the Hubble expansion rate squared on the left hand side, which governs the evolution of spacetime. The right side includes all the different forms of matter and energy, along with spatial curvature (in the final term), which determines how the Universe evolves in the future. This has been called the most important equation in all of cosmology and was derived by Friedmann in essentially its modern form back in 1922.

What you see, above, is sometimes known as the first Friedmann equation: what I myself have often called the most important equation in the Universe. In any Universe that you can imagine that is:

• governed by Einstein’s General Relativity,
• that’s isotropic (i.e., the same in all directions),
• and that’s homogeneous (i.e., the same at all locations),

Einstein’s field equations can be solved, exactly, to give you a series of equations. One of them is this very equation, and its power is that it relates the change in the scale of the Universe, on the left hand side, to the matter, energy, and curvature (and cosmological constant, if you include it) on the right hand side.

The simplest way to deal with this equation is to assume there’s no curvature and no cosmological constant, and to imagine that you’ve got a Universe that’s filled with only one type of matter-or-energy in it. You’re going to get a much simpler equation: one that simply says that the change in the scale of the Universe (given by H on the left hand side, which technically is the “change in scale” squared, since it’s H²) to some form of energy density (given by ρ on the right hand side, since we’re setting the curvature, k, and the cosmological constant, Λ, to zero), and let’s not even worry about those constants in front of the ρ.

Then, I want us to imagine three possibilities for what sort of energy could be in this imaginary Universe: matter, radiation, and “dark energy.”

This diagram shows, to scale, how spacetime evolves/expands in equal time increments if your Universe is dominated by matter, radiation, or the energy inherent to space itself (i.e., during inflation or dark energy dominance), with the latter corresponding to the inflationary phase that preceded and set up the hot Big Bang. Although all of these model universes expand toward infinite size, they approach it at different rates, with the “space itself” solution approaching infinity in a fundamentally more quick fashion than the other two.

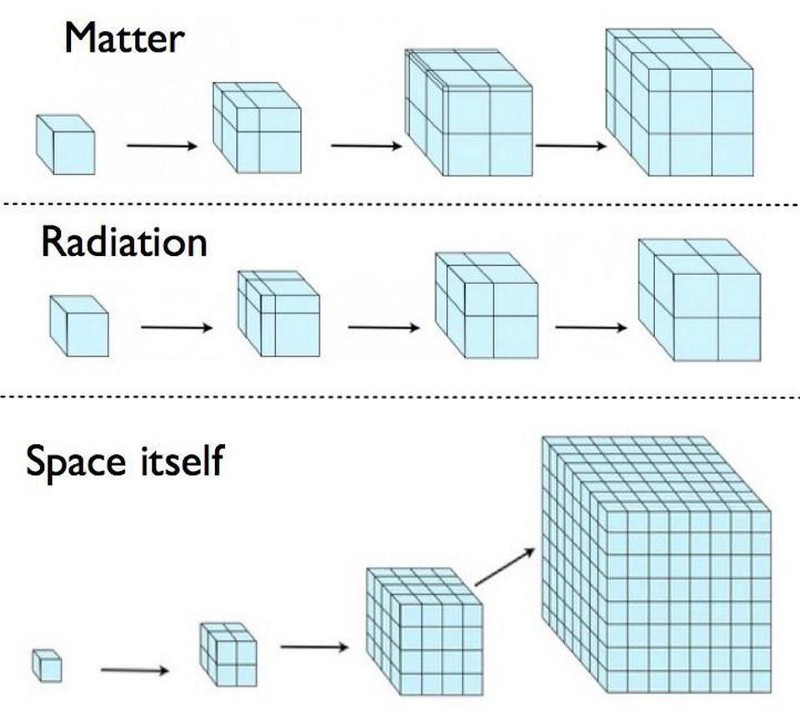
What’s going to happen is that the “change in scale, squared” (H²) is going to change in proportion to how the energy density (ρ) changes. Let’s break them down, one by one.

1. For matter, density is just mass over volume. Because particles have a fixed mass and a fixed number, then the density changes inversely proportional to the volume: double the “scale” of the Universe and your density becomes 1/8 of what it was initially; halve the “scale” of the Universe and your density increases by a factor of 8. So the “change in scale” is just the square root of that.
2. For radiation, those quanta are massless, so density is just energy over volume. While the number of quanta (say, photons) is fixed, the energy of each quantum is defined by its wavelength, and the “length” of one wave is dependent on the scale of the Universe. As a result, not only does volume change if you double or halve the scale of your Universe, but the energy-per-quantum halves or doubles, respectively. If you double the scale of your Universe, the density becomes 1/16 of what it was initially; if you halve the scale instead, your density increases by a factor of 16. And again, the “change in scale” is the square root of that.
3. But for dark energy, this behaves as a form of energy intrinsic to space itself: its energy density is always constant. Whether you change the volume or not, that density term, ρ, remains unchanged. If you halve or double the scale of the Universe, the “change in scale” is simply the square root of a constant: it does not change.

How matter (top), radiation (middle), and dark energy (bottom) all evolve with time in an expanding Universe. As the Universe expands, the matter density dilutes, but the radiation also becomes cooler as its wavelengths get stretched to longer, less energetic states. Dark energy’s density, on the other hand, will truly remain constant if it behaves as is currently thought: as a form of energy intrinsic to space itself. These three components, together, dictate how the Universe expands at all times from the Big Bang until the present day.

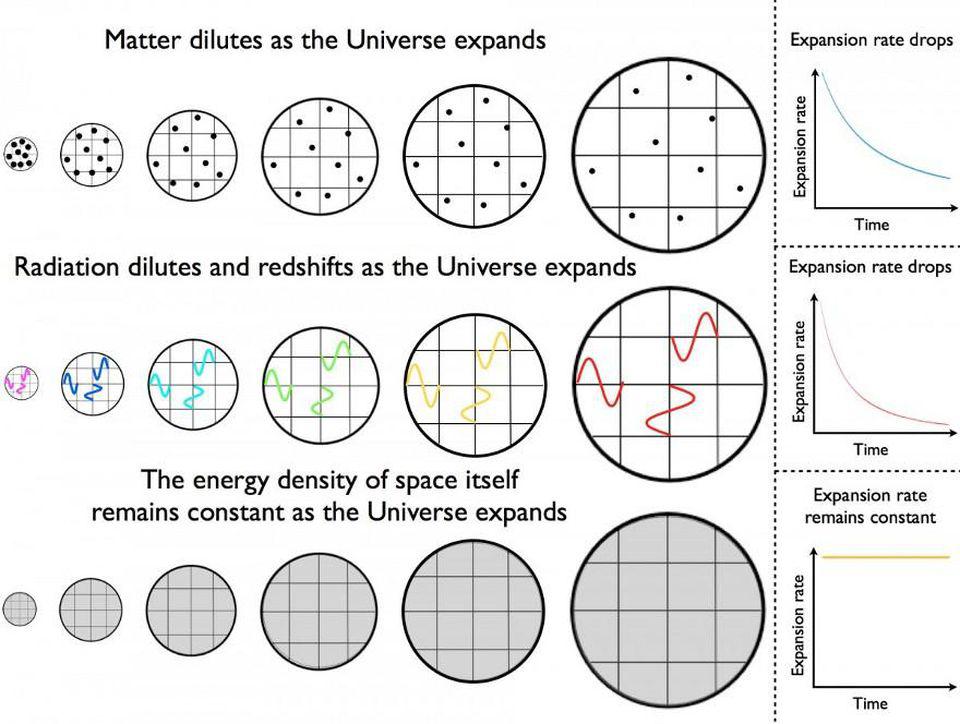
Because we’re not dealing with an equation about the “change in scale” but rather an equation that tells us something about the “change in scale, squared,” there’s an important caveat here: the value of the “change in scale” itself could be either positive or negative, and we’d get the same answer either way. If the “change in scale” were positive, the Universe would be expanding; if the “change in scale” were negative, the Universe would be contracting.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

What Einstein’s initial (and flawed) reasoning told him was, “Hey, if you start your Universe off static and neither expanding nor contracting, then if you sprinkle matter into it, it must begin contracting. So if we don’t want it to contract, we can add in another form of energy that behaves differently (like dark energy, or a cosmological constant), and watch the Universe expand instead. And if we tune the matter and the other form of energy just right, they’ll balance, and we’ll get a static Universe instead!”

But observationally, as was first borne out in the 1920s and that’s been confirmed ever since to much greater precision and to extraordinary distances, the Universe is actually expanding, and contains all three of these species: matter, radiation, and dark energy.

A plot of the apparent expansion rate (y-axis) vs. distance (x-axis) is consistent with a Universe that expanded faster in the past, but where distant galaxies are accelerating in their recession today. This is a modern version of, extending thousands of times farther than, Hubble’s original work. Note the fact that the points do not form a straight line, indicating the expansion rate’s change over time. The fact that the Universe follows the curve it does is indicative of the presence, and late-time dominance, of dark energy.

If we want to know, then, how the Universe expands, and how the expansion accelerates, all we have to do is solve that same governing equation, the first Friedmann equation, for a Universe with all three types of energy, and choose the positive, expanding solution.

That’s actually a fairly straightforward task! It turns out that the expansion rate itself — what we define as the “change in scale” parameter, or H — actually always decreases over time. This value is not something that accelerates, but rather something that decreases: rapidly early on, when the Universe is dominated by radiation, then a little less rapidly later, when the Universe is dominated by matter, and then eventually, when dark energy takes over, slowing down further and approaching a finite, positive, non-zero value.

The reason we say the expansion is accelerating isn’t because H, the expansion rate, is increasing over time; it is not. The reason is because the things we observe are galaxies within the Universe, and we can see these galaxies receding from us. If we watched these galaxies recede over time, then we’d find:

• when the Universe is dominated by radiation, the apparent recession speed of these galaxies would decrease,
• when the Universe is dominated by matter, their apparent recession speed would decrease, but more slowly,
• and when the Universe is dominated by dark energy, their apparent recession speed increases.

It’s that — the rate at which galaxies appear to recede from us — that’s accelerating, not the expansion rate of the Universe itself.

The scale of the Universe (y-axis) versus the age of the Universe (x-axis) on logarithmic scales. Some size and time milestones are marked, as appropriate. The transition between radiation and matter domination is subtle; the transition to dark energy domination is easy to see.

It’s important to recognize that dark energy isn’t some type of “negative energy” or “repulsive gravity,” although there are certainly people out there who attempt to interpret it in that fashion. Instead, it’s just a form of energy like any other, and that it’s part of that great cosmic balance between the expansion of the Universe and the sum of all the different forms of energy within it. The biggest difference is that while matter’s and radiation’s energy densities both drop as the Universe expands, dark energy’s energy density doesn’t: it remains constant instead, and that “lack of dropping” is why the individual galaxies caught up in our cosmic expansion are seen to speed away from us faster and faster as time goes on.

At the same time, however, it’s important to remember that we aren’t 100% certain that dark energy truly behaves as though its energy density is constant: like a true cosmological constant. Dark energy could, ever so slightly, increase or decrease in density or in strength as time progresses. Part of the reason for NASA’s next upcoming flagship mission, the Nancy Roman Space Telescope, is to make the key measurements that tell us, to the greatest precision ever, how dark energy truly behaves. After all, the ultimate fate of the Universe depends on it!

Send in your Ask Ethan questions to startswithabang at gmail dot com!