Ask Ethan: Is our Universe a hologram?

Have you ever wondered whether there’s more to reality than what we can see, perceive, detect, or otherwise observe? One of the most intriguing but speculative ideas of 20th and 21st century physics is the notion that our Universe, which seems to consist of three spatial and one temporal dimension, might possess additional, extra dimensions beyond the ones we can see. Originally thought up independently by Theodr Kaluza and Oskar Klein in an attempt to unify Einstein’s General Relativity with Maxwell’s electromagnetism, the idea lives on in the modern context of quantum field theory and a specific extension of its ideas: string theory.

But for all of its mathematical beauty and elegance, does it have anything to do with our physical Universe? That’s what our Patreon supporter Benhead, who was thinking about this recent New York Times piece, wrote to inquire about:

“I’ve never really bought into the holographic thing as a physical concept. I’m not even sure how well it works as a mathematical abstraction… in the analogy I thought we were the image but what was “real” was the film.”

The idea that the Universe is a hologram — also known as the holographic principle or the holographic Universe — is more than 20 years old now, but remains both as curious and as problematic as ever. Here’s an overview of the concept.

This hologram of a DNA molecule’s double helix structure is projected with the use of mirrors, displaying a true three-dimensional appearance from any angle. This is because it’s possible, through the use of coherent light, to create a map of the light field of an object and encode it onto a flat surface.

What is a conventional hologram?

If you’ve ever seen a hologram before, you’ve truly beheld a wondrous application of the optical behavior of light. Printed onto a two-dimensional surface, a hologram — when it catches the light just right — shows you not a standard two-dimensional image like you’d typically see, but a fully three-dimensional image. Not only can the third dimension, depth, be readily perceived by your eyes, but as you change your viewing angle with respect to the hologram, the relative distance from your eye to various parts of the encoded, holographic image appears to change correspondingly as well.

It appears as though, behind the “surface” of the hologram, a fully three-dimensional world exists, and you can see its details just as surely as you could see the three-dimensional world reflected in a mirror.

This is because a hologram isn’t simply a static image, but rather a “light map” of the three dimensional object/setting that went into creating the hologram itself. Creating a hologram is itself an instructive look at how light, optics, and physics come together to encode a higher-dimensional set of information onto a lower-dimensional surface.

Although a photograph encodes an image of the three-dimensional world onto a two-dimensional surface, the three-dimensional information about depth is flattened and lost. The difference between a photograph and a hologram is all about having not just a light image, but a light field encoded and mapped onto the lower-dimensional surface.

The way a photograph works, by contrast to a hologram, is very simple. Take light that’s emitted or reflected from an object, focus it through a lens, and record it onto a flat surface. That’s not only how photography works, but also how you physically see objects biologically, as the lens in your eyeball focuses the light onto your retina, where the rods and cones on the back of your eye record it, send it to your brain, and there it gets processed into an image.

But by using coherent light, such as that from a laser, and a special emulsion on the recording surface, you’re no longer limited to recording a light image, but rather you can record and create a map of the entire light field. Part of the information encoded in a light field is the three-dimensional position of every object within the image, including features such as:

• variations in density,
• textures,
• opacity,
• and relative distance.

All of these properties are encoded in the light field, and are faithfully recorded onto the two-dimensional hologram surface. When that surface is then properly illuminated, it will display to any observer the full suite of recorded three-dimensional information, and will do so from every possible perspective that it’s viewable from. By printing this two-dimensional light field/map onto a metallic film, you can create a conventional hologram.

This photograph of a hologram at the MIT museum looks like a three-dimensional object, but is only a two-dimensional light field encoded onto the surface of a hologram. Holograms are lower-dimensional surfaces that encode information about the entire higher-dimensional object within the higher-dimensional space. The idea of the holographic principle is that our Universe and the quantum field theoretical laws that describe it is the surface of a higher-dimensional spacetime that includes quantum gravity.

Are there other physical applications of this idea?

The big idea behind a hologram is actually ubiquitous in physics: the notion that you can examine a lower-dimensional surface and obtain not only substantial information about the higher-dimensional reality that is encoded on it, but complete information that reveals to you the full set of physical properties concerning that higher-dimensional reality. The key is to have the lower-dimensional surface serve as the boundary of your higher-dimensional space; if you can both:

• understand the laws that govern your higher-dimensional space,
• and measure enough of the properties that are encoded on the surface that bounds that space,

you can then draw conclusions about the precise physical state that occurs inside that region, fully.

You can accomplish this in electromagnetism, for example, by measuring any of three properties on the surface enclosing the region: with Dirichlet, Neumann, or Robin boundary conditions. You can do something analogous in General Relativity, with the caveat that if you’re not dealing with a closed spacetime manifold, you must add an additional boundary term. In many areas of physics, if you know the laws that govern the boundary and the region of space that it encloses, simply measuring enough of the properties encoded on the boundary enables you to determine the full set of physical properties that describe the inside.

This set of radiofrequency cavities within a linear accelerator in Australia consist of a very intricate electromagnetic setup. If you were to draw an imaginary two-dimensional boundary around any region either inside or outside this cavity, the information encoded on the surface, if you measured enough of it, could tell you what was going on in the volume inside that boundary as well.

This type of analysis even has applications to black holes, although they’ve only ever been tested in quantum analogue systems, as we have yet to actually measure a black hole precisely enough to test the idea. In theory, whenever individual quanta fall into a black hole — and remember, black holes are fundamentally entities that exist in our Universe with three spatial dimensions — they carry all the quantum information that they previously possess with them into the black hole.

But when black holes decay, which they do via the emission of Hawking radiation, the radiation that comes out should simply possess a blackbody spectrum, with no memory of things like the mass, charge, spin, polarization, or baryon/lepton number of the quanta that went into creating them. This non-conservative property is known as the black hole information paradox, with the only two realistic possibilities being that either information is not conserved, after all, or that the information must somehow escape the black hole’s clutches during the process of evaporation.

It’s possible, even likely, that there’s a two dimensional surface, either on or interior to the event horizon, where all of the information that went into and radiated away from the black hole is preserved. It’s possible that the holographic principle, as applied to black holes, can actually solve the black hole information paradox, preserving unitarity (the idea that the sum of the probabilities of all possible outcomes must add up to 1) in the process.

Encoded on the surface of the black hole can be bits of information, proportional to the event horizon’s surface area. When the black hole decays, it decays to a state of thermal radiation. Whether that information survives and is encoded in the radiation or not, and if so, how, is not a question that our current theories can provide the answer to.

Is our Universe holographic in nature?

Now, here we are, in what appears to us to be a four-dimensional spacetime: with three spatial and one temporal dimension. But what if this isn’t representative of the full picture of reality; what if there are:

• more dimensions out there,
• that simply are inaccessible to us,
• and that what we perceive as our four-dimensional Universe is actually the boundary of a higher-dimensional entity that represents, somehow, our “true” Universe?

It’s a wild idea, but one that has its roots in a seemingly unrelated discipline: String Theory.

String Theory grew from a proposal — the string model — to explain the strong interactions, as the insides of protons, neutrons and other baryons (and mesons) were known to have a composite structure. It gave a whole bunch of nonsensical predictions, though, that didn’t correspond to experiments, including the existence of a spin-2 particle. But people recognized if you took that energy scale way up, toward the Planck scale, the string framework could unify the known fundamental forces with gravity, and thus String Theory was born.

The idea that the forces, particles and interactions that we see today are all manifestations of a single, overarching theory is an attractive one, requiring extra dimensions and lots of new particles and interactions. Many such mathematical constructs exist to explore, but without a physical Universe to compare it to, we’re unlikely to learn anything meaningful about our Universe.

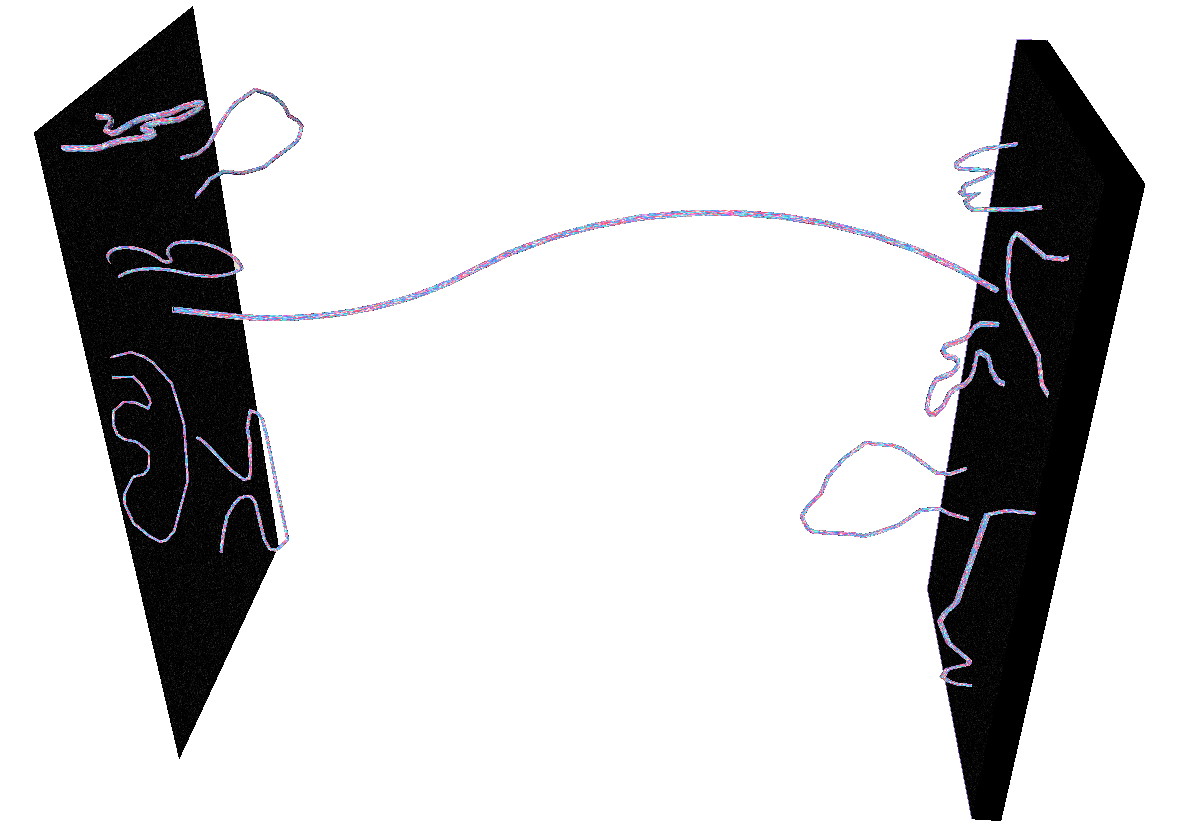
A feature (or flaw, depending on how you look at it) of this attempt at a “holy grail” of physics is that it absolutely requires a large number of extra dimensions. So a big question then becomes how do we get our Universe, which has just three spatial dimensions, out of a theory that gives us many others? And which string theory, since there are many possible realizations of string theory, is the right one?

Perhaps, the realization goes, the many different string theory models and scenarios that are out there are actually all different aspects of the same fundamental theory, seen from a different point of view. In mathematics, two systems that are equivalent to one another are known as “dual,” and one surprising discovery that’s related to a hologram is that sometimes two systems that are dual to one another have different numbers of dimensions.

The reason physicists get very excited about this is that in 1997, physicist Juan Maldacena proposed the AdS/CFT correspondence, which claimed that our three dimensional (plus time) Universe, with its quantum field theories describing elementary particles and their interactions, was dual to a higher-dimensional spacetime (anti-de Sitter space) that plays a role in quantum theories of gravity.

The idea that a higher-dimensional space, often called the bulk, is mathematically equivalent to a lower-dimensional space that defines the boundary of the bulk, known as the brane, is the core idea at the root of the AdS/CFT correspondence. This lower-dimensional analogue of the 5-to-4 dimensional relation derived by Juan Maldacena in 1997 is shown here.

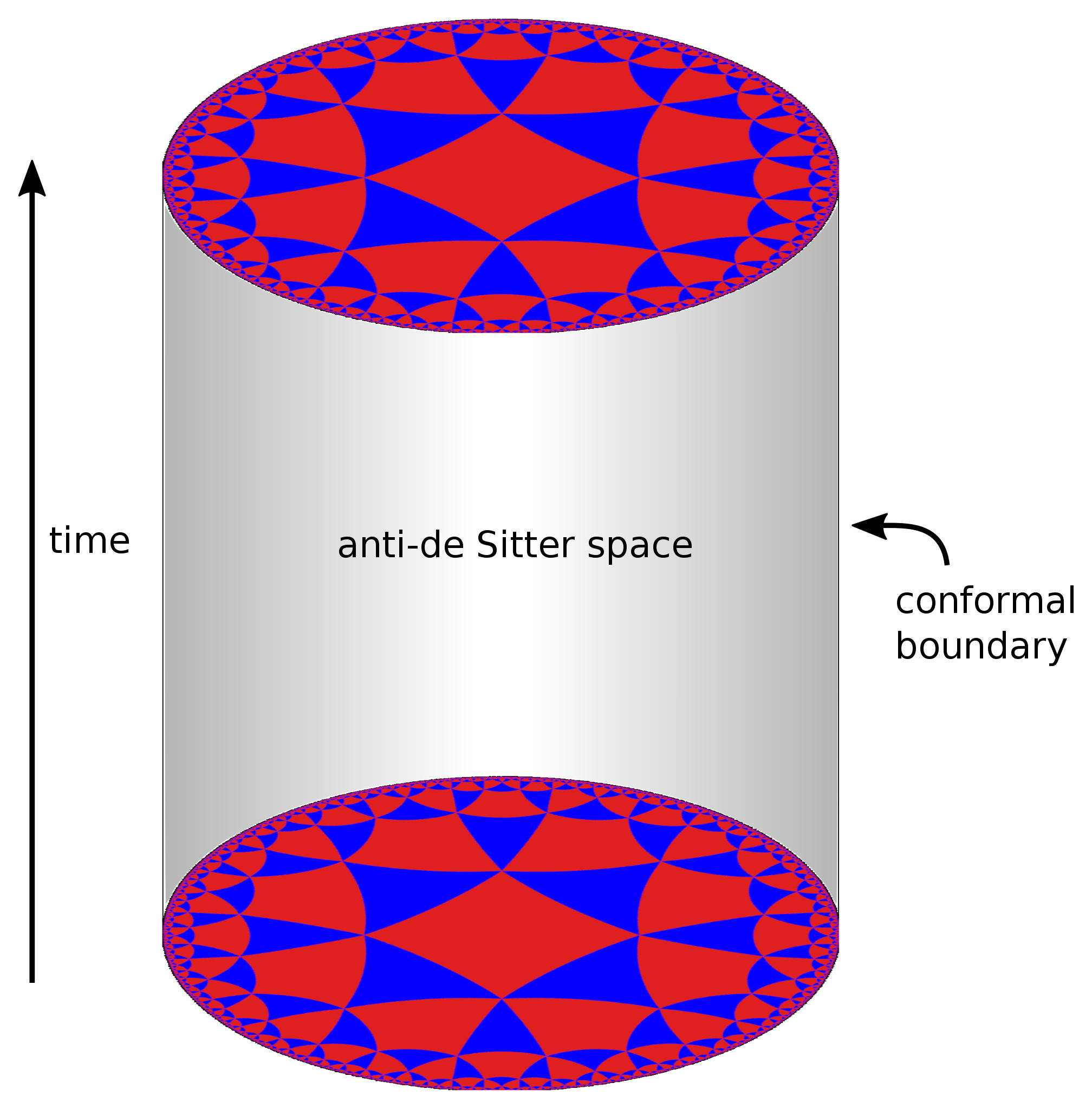
For the past 25 years, physicists and mathematicians have explored this correspondence to the best of our abilities, and it turns out that it has been usefully applied to a number of condensed matter and solid state physical systems. As far as applications to our entire Universe, however, and specifically to a framework where we have to have at least 10 dimensions total (as required by String Theory), we run into a significant set of problems that have not been so easy to solve.

For one, we’re very certain we don’t live in anti-de Sitter space, because we’ve measured the effects of dark energy, and those effects show us that the Universe’s expansion is accelerating in a fashion that’s consistent with a positive cosmological constant. A spacetime with a positive cosmological constant looks like de Sitter space, and specifically not like anti-de Sitter space, which would have a negative cosmological constant. Mathematically, because of a series of problems (like the bubble nucleation/percolation problem) that arise in de Sitter space and not in anti-de Sitter space, we cannot build that same correspondence.

The string landscape might be a fascinating idea that’s full of theoretical potential, but it cannot explain why the value of such a finely-tuned parameter like the cosmological constant, the initial expansion rate, or the total energy density have the values that they do. One of the more important deficiencies of the AdS/CFT correspondence is that “AdS” stands for anti-de Sitter space, which requires a negative cosmological constant. However, the observed Universe has a positive cosmological constant, implying de Sitter space; there is no equivalent dS/CFT correspondence.

For another, the only dualities we’ve ever discovered relate the properties of the higher-dimensional space to its lower-dimensional boundary: a reduction in dimension by one. Two-dimensional holograms can only encode three-dimensional information; the four-dimensional conformal field theories (CFTs) that are part of the AdS/CFT correspondence only apply to five-dimensional anti-de Sitter spaces. The question of compactification — of how you get down to no more than five dimensions in the first place — remains unaddressed.

However, there’s another aspect of the AdS/CFT correspondence that many find compelling. Sure, those two problems are real: we have the wrong sign for the cosmological constant and the wrong number of dimensions. However, when two spaces of different dimensions are mathematically dual to one another, one can sometimes obtain more information about the higher-dimensional space than you might initially think. Sure, there’s less information available on a lower-dimensional boundary of a surface than inside the volume of the full space enclosed by the surface. That implies that when you measure one thing that’s happening on the boundary’s surface, you might wind up learning multiple things that are occurring inside of the larger, higher-dimensional volume.

The idea that two quanta could be instantaneously entangled with one another, even across large distances, is often talked about as the spookiest part of quantum physics. If reality were fundamentally deterministic and were governed by hidden variables, this spookiness could be removed. Unfortunately, attempts to do away with this type of quantum weirdness have all failed, with conjectures like the AdS/CFT correspondence, which could involve an underlying objective reality, all requiring something exotic and unproven, such as the invocation of extra dimensions and negative energy.

One wild possibility — potentially related to 2022’s Nobel Prize in physics on quantum entanglement — is that something occurring in the larger-dimensional space may wind up relating two disparate, seemingly disconnected regions along the lower-dimensional boundary. If you’re bothered by the notion that measuring one entangled particle appears to give you information about the other entangled pair instantaneously, appearing as though communication is occurring faster-than-light, the holographic principle might be your best hope for a physically-rooted savior.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Nevertheless, the past 25 years have arguably brought us no closer to finding extra dimensions, understanding whether or not they’re relevant for our reality, or delivering any important theoretical insights that help us better comprehend our own Universe. Duality, however, cannot be denied: it is a mathematical fact. The AdS/CFT correspondence will continue to be mathematically interesting, but the two major problems with it:

• that it delivers the observably wrong sign for dark energy,
• and that it only works for five dimensions, not the ten (or more) needed for String Theory,

loom large and remain unaddressed. The idea that the Universe is a hologram, known as the holographic Universe, may indeed someday lead us to quantum gravity. Until these puzzles are solved, however, it’s impossible to foresee how we’ll get there.

Send in your Ask Ethan questions to startswithabang at gmail dot com!