The fundamental problem with gravity and quantum physics

No matter what you may have heard, make no mistake: physics is not “over” in any sense of the word. As far as we’ve come in our attempts to make sense of the world and Universe around us — and we have come impressively far — it’s absolutely disingenuous to pretend that we’ve solved and understood the natural world around us in any sort of satisfactory sense. We have two theories that work incredibly well: in all the years we’ve been testing them, we’ve never found a single observation or made a single experimental measurement that’s conflicted with either Einstein’s General Relativity or with the Standard Model’s predictions from quantum field theory.

If you want to know how gravitation works or what its effects on any object in the Universe will be, General Relativity has yet to let us down. From tabletop experiments to atomic clocks to celestial mechanics to gravitational lensing the formation of the great cosmic web, its success rate is 100%. Similarly, for any particle physics experiment or interaction conceivable, whether mediated via the strong, weak, or electromagnetic force, the Standard Model’s predictions have always been found to agree with the results. In their own realms, General Relativity and the Standard Model can each lay claim to be the most successful physics theory of all-time.

But there’s a huge fundamental problem at the heart of both of them: they simply don’t work together. If you want your Universe to be consistent, this situation simply won’t do. Here’s the fundamental problem at the heart of physics in the 21st century.

Countless scientific tests of Einstein’s General Theory of Relativity have been performed, subjecting the idea to some of the most stringent constraints ever obtained by humanity. Einstein’s first solution was for the weak-field limit around a single mass, like the Sun; he applied these results to our Solar System with dramatic success. Very quickly, a handful of exact solutions were found thereafter.

On the one hand, General Relativity, our theory of gravity, was a radical concept when it first came out: so radical that it was attacked by many on both philosophical and physical grounds for many decades.

• How could space and time not be absolute quantities; how could they be different for everyone dependent on the particular properties of whoever’s observing it?
• How could gravitation not be instantaneous between any two objects that would attract; how can this interaction only propagate at a finite speed that was equal to the speed of light?
• How could gravity not only affect masses, but all forms of energy, including massless objects like light?
• Conversely, how could all forms of energy, not just mass, affect how all other objects in the Universe experienced the effects of gravity?
• And how could there be an underlying, warped-and-curved geometry to the Universe that determined how objects moved?

Regardless of how anyone might have felt about the new picture that Einstein’s greatest achievement, the general theory of relativity, brought along with it, the behavior of physical phenomena in the Universe doesn’t lie. Based on a whole suite of experiments and observations, General Relativity has proven to be a remarkably successful description of the Universe, succeeding under every conceivable condition that we’ve been able to test, whereas no other alternative does.

The results of the 1919 Eddington eclipse expedition showed, conclusively, that the General Theory of Relativity described the bending of starlight around massive objects, overthrowing the Newtonian picture. This was the first observational confirmation of Einstein’s theory of gravity.

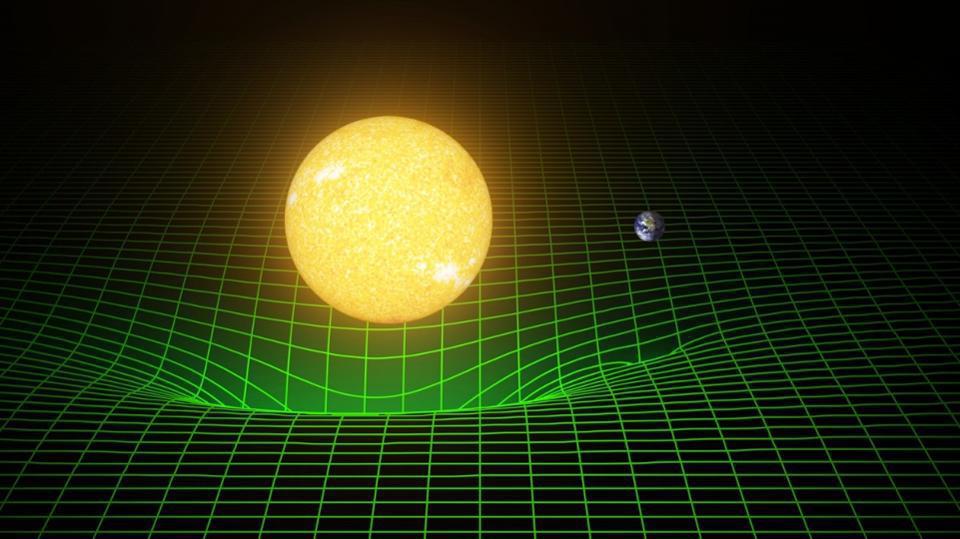
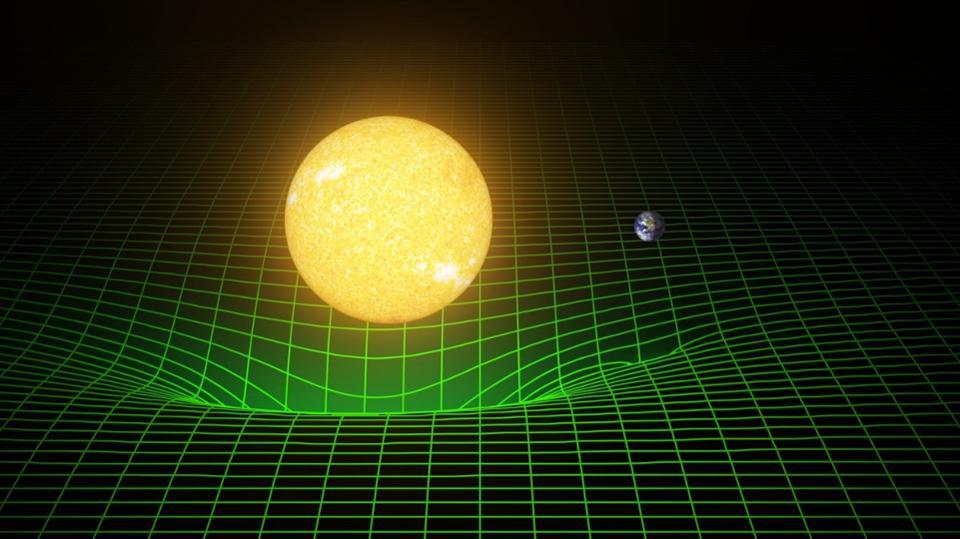
What General Relativity tells us is that the matter-and-energy in the Universe — specifically, the energy density, the pressure, the momentum density, and the shear stress present throughout spacetime — determines the amount and type of spacetime curvature that’s present in all four dimensions: the three spatial dimensions as well as the time dimension. As a result of this spacetime curvature, all entities that exist in this spacetime, including (but not limited to) all massive and massless particles, move not necessarily along straight lines, but rather along geodesics: the shortest paths between any two points defined by the curved space between them, rather than an (incorrectly) assumed flat space.

Where spatial curvature is large, the deviations from straight-line paths are large, and the rate at which time passes can dilate significantly as well. Experiments and observations in laboratories, in our Solar System, and on galactic and cosmic scales all bear this out in great agreement with General Relativity’s predictions, lending further support to the theory.

Only this picture of the Universe, at least so far, works to describe gravitation. Space and time are treated as continuous, not discrete, entities, and this geometric construction is required to serve as the “background” spacetime in which all interactions, including gravitation, take place.

According to the Standard Model, the leptons and antileptons should all be separate, independent particles from one another. But the three types of neutrino all mix together, indicating they must be massive and, furthermore, that neutrinos and antineutrinos may in fact be the same particle as one another: Majorana fermions.

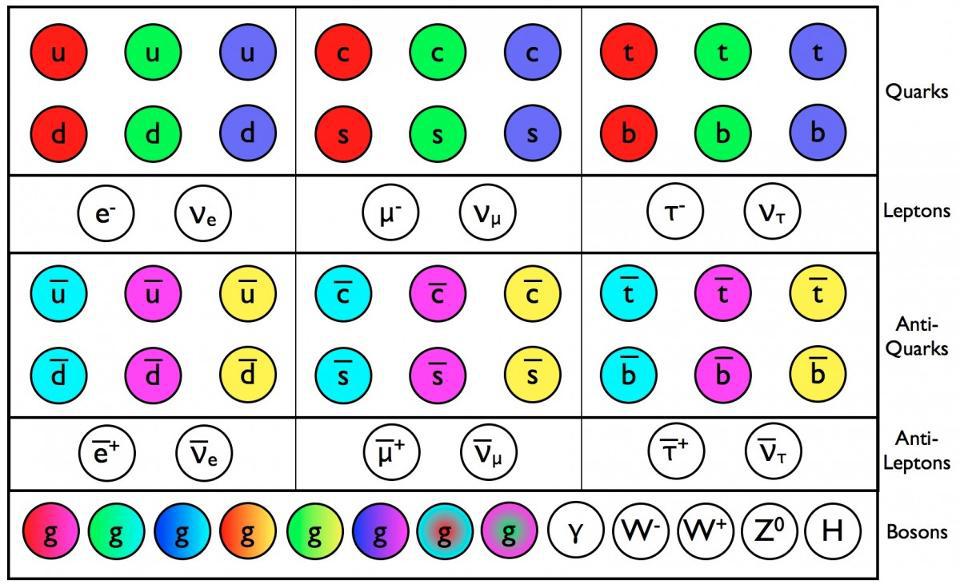
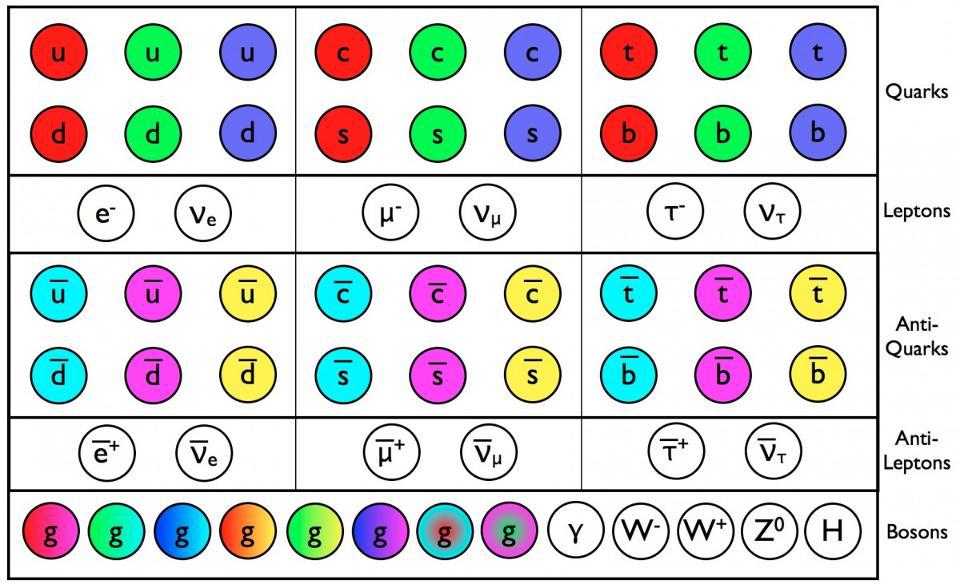
On the other hand, there’s the Standard Model of particle physics. Originally formulated under the assumptions that neutrinos were massless entities, the Standard Model is based on quantum field theory, where there are:

• fermionic quanta (particles) that have charges,
• bosonic quanta (also particles) that mediate the forces between particles with the relevant charge,
• and a (quantum) vacuum of spacetime through which all of the quanta travel and interact.

The electromagnetic force is based on electric charges, and so all six of the quarks and the three charged leptons (electron, muon, and tau) all experience the electromagnetic force, whereas the massless photon mediates it.

The strong nuclear force is based on color charges, and only the six quarks possess them. There are eight massless gluons that mediate the strong force, and no other particles are involved in it.

The weak nuclear force, meanwhile, is based on weak hypercharge and weak isospin, and all of the fermions possess at least one of them. The weak interaction is mediated by the W-and-Z bosons, and the W bosons also possess electric charges, meaning they experience the electromagnetic force (and can exchange photons) as well.

The inherent width, or half the width of the peak in the above image when you’re halfway to the crest of the peak, is measured to be 2.5 GeV: an inherent uncertainty of about +/- 3% of the total mass. The mass of the particle in question, the Z boson, is peaked at 91.187 GeV, but that mass is inherently uncertain by a significant amount owing to its excessively short lifetime. This result it remarkably consistent with Standard Model predictions.

There’s a rule in quantum physics that all identical quantum states are indistinguishable from one another, and that enables them to mix together. Quark mixing was expected and then confirmed, with the weak interaction determining various parameters of this mixing. Once we learned that neutrinos were massive, not massless as originally expected, we realized that the same type of mixing must occur for neutrinos, also determined by the weak interactions. This set of interactions — the electromagnetic, weak, and strong nuclear forces, acting upon the particles that have the relevant and necessary charges — describes everything that one could want to predict particle behavior under any imaginable conditions.

And the conditions we’ve tested them under are extraordinary. From cosmic ray experiments to radioactive decay experiments to solar experiments to high-energy physics experiments involving particle colliders, the Standard Model’s predictions have agreed with every single such experiment ever performed. Once the Higgs boson was discovered, it confirmed our picture that the electromagnetic and weak force were once unified at high energies into the electroweak force, which was the ultimate test of the Standard Model. In all of physics history, there’s never been a result the Standard Model couldn’t explain.

Today, Feynman diagrams are used in calculating every fundamental interaction spanning the strong, weak, and electromagnetic forces, including in high-energy and low-temperature/condensed conditions. Including higher-order “loop” diagrams leads to more refined, more accurate approximations of the true value to quantities in our Universe.

But there’s a catch. All of the Standard Model calculations we perform are based on particles that exist in the Universe, which means they exist in spacetime. The calculations we typically perform are done so under the assumption that spacetime is flat: an assumption that we know is technically wrong, but one that’s so useful (because calculations in curved spacetime are so much more difficult than they are in flat space) and such a good approximation to the conditions we find on Earth that we plow ahead and make this approximation anyway.

After all, this is one of the great methods we use in physics: we model our system in as simple a fashion as possible in order to capture all of the relevant effects that will determine the outcome of an experiment or measurement. Saying “I’m doing my high-energy physics calculations in flat spacetime” rather than in curved spacetime doesn’t give you an appreciably different answer except in the most extreme conditions.

But extreme conditions do exist in the Universe: in the spacetime around a black hole, for example. Under those conditions, we can determine that using a flat spacetime background is simply no good, and we’re compelled to take on the herculean task of performing our quantum field theory calculations in curved space.

An illustration of heavily curved spacetime for a point mass, which corresponds to the physical scenario of being located outside the event horizon of a black hole. As you get closer and closer to the mass’s location in spacetime, space becomes more severely curved, eventually leading to a location from within which even light cannot escape: the event horizon. The radius of that location is set by the mass, charge, and angular momentum of the black hole, the speed of light, and the laws of General Relativity alone. Quite remarkably, if you replace “r/R” with the inverse of it, “R/r”, you can map the interior of a black hole onto the exterior and vice versa, transforming your solution for a black hole into one for a white hole.

It might surprise you that, in principle, this isn’t really all that difficult. All you have to do is replace the flat spacetime background you normally use for performing your calculations with the curved background as described by General Relativity. After all, if you know how your spacetime is curved, you can write down the equations for the background, and if you know what quanta/particles you have, you can write down the remaining terms describing the interactions between them in that spacetime. The rest, although it’s quite difficult in practice under most circumstances, is simply a matter of computational power.

You can describe, for example, how the quantum vacuum behaves inside and outside of a black hole’s event horizon. Because you’re in a region where spacetime is more severely curved the closer you are to a black hole’s singularity, the quantum vacuum differs in a calculable way. The difference in what the vacuum state is in different regions of space — particularly in the presence of a horizon, whether a cosmological or an event horizon — leads to the production of radiation and particle-antiparticle pairs wherever quantum fields are present. This is the fundamental reason behind Hawking radiation: the reason that black holes, in a quantum Universe, are fundamentally unstable and will eventually decay.

Although no light can escape from inside a black hole’s event horizon, the curved space outside of it results in a difference between the vacuum state at different points near the event horizon, leading to the emission of radiation via quantum processes. This is where Hawking radiation comes from, and for the lowest-mass black holes ever discovered, Hawking radiation will lead to their complete decay in ~10^68 years. For even the largest mass black holes, survival beyond 10^103 years or so is impossible due to this exact process. The higher mass your black hole is, the weaker Hawking radiation is and the longer it will take to evaporate.

That’s as far as we can go, however, and that doesn’t take us everywhere. Yes, we can make the Standard Model and General Relativity “play nice” in this fashion, but this only allows us to calculate how the fundamental forces work in strongly curved spacetimes that are sufficiently far away from singularities, like those at the centers of black holes or — in theory — at the very beginning of the Universe, assuming that such a beginning exists.

The maddening reason is that gravity affects all types of matter and energy. Everything is affected by gravitation, including, in theory, whatever types of particles are ultimately responsible for gravitation. Given that light, which is an electromagnetic wave, is made up of individual quanta in the form of photons, we assume that gravitational waves are made up of quanta in the form of gravitons, which we even know many of the particle properties of in the absence of a full quantum theory of gravitation.

But that’s precisely what we need. That’s the missing piece: a quantum theory of gravity. Without it, we cannot understand or predict any of the quantum properties of gravity. And before you say, “What if they don’t exist?” know that wouldn’t paint a consistent picture of reality.

The wave pattern for electrons passing through a double slit, one-at-a-time. If you measure “which slit” the electron goes through, you destroy the quantum interference pattern shown here. Regardless of the interpretation, quantum experiments appear to care whether we make certain observations and measurements (or force certain interactions) or not.

For example, consider the most “inherently quantum” of all the quantum experiments that have ever been performed: the double slit experiment. If you send a single quantum particle through the apparatus and you observe which slit it goes through as it goes through it, the outcome is completely determined, as the particle behaves as though it

• was going to go through,
• goes through,
• and went through,

the slit you observed it to go through at every step of the way. If that particle was an electron, you could determine what its electric and magnetic fields were during its entire journey. You could also determine what its gravitational field was (or equivalently, what its effects on the curvature of spacetime were) at every moment as well.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

But what if you don’t observe which slit it goes through? Now the electron’s position is indeterminate until it gets to the screen, and only then can you determine “where” it is. Along its journey, even after you make that critical measurement, its past trajectory is not fully determined. Because of the power of quantum field theory (for electromagnetism), we can determine what its electric field was. But because we don’t have a quantum theory of gravitation, we cannot determine its gravitational field or effects. In this sense — as well as at small, quantum fluctuation-rich scales or at singularities in which classical General Relativity gives only nonsense answers — we don’t fully understand gravitation.

Quantum gravity tries to combine Einstein’s General theory of Relativity with quantum mechanics. Quantum corrections to classical gravity are visualized as loop diagrams, as the one shown here in white. If you extend the Standard Model to include gravity, the symmetry that describes CPT (the Lorentz symmetry) may become only an approximate symmetry, allowing for violations. Thus far, however, no such experimental violations have been observed.

This works both ways: because we don’t understand gravitation at a quantum level, that means we don’t quite understand the quantum vacuum itself. The quantum vacuum, or the properties of empty space, is something that can be measured in various ways. The Casimir effect, for instance, lets us measure the effect of the electromagnetic interaction through empty space under a variety of setups, simply by changing the configuration of conductors. The expansion of the Universe, if we measure it over all of our cosmic history, reveals to us the cumulative contributions of all of the forces to the zero-point energy of space: the quantum vacuum.

But can we quantify the quantum contributions of gravitation to the quantum vacuum in any way?

Not a chance. We don’t understand how to calculate gravity’s behavior at high energies, at small scales, near singularities, or when quantum particles exhibit their inherently quantum nature. Similarly, we don’t understand how the quantum field that underpins gravity — assuming there is one — behaves at all under any circumstances. This is why attempts to understand gravity at a more fundamental level must not be abandoned, even if everything we’re doing now turns out to be wrong. We’ve actually managed to identify the key problem that needs to be solved to push physics forward beyond its current limitations: a huge achievement that should never be underestimated. The only options are to keep trying or give up. Even if all of our attempts turn out to ultimately be in vain, it’s better than the alternative.