Top 5 facts about Imaginary Math
You know that the square root of -1 is “i”, an imaginary number. But did you know any of these?
“There is not enough love and goodness in the world to permit giving any of it away to imaginary beings.” -Friedrich Nietzsche
Sometimes, if you want to describe the Universe you live in accurately, you need to go beyond conventional ways of thinking. In the early part of the 20th century, two revolutions in physics — Einstein’s relativity (first special, then general) and quantum mechanics — brought in the need for mathematics beyond what the real numbers could bring us alone. Ever since, complex mathematics, consisting of both real and imaginary parts, has been inextricably intertwined with our understanding of the Universe.
Mathematically, when we think about numbers, we can think about a few different ways to categorize them:
- The countable numbers: 1, 2, 3, 4, etc. There are an infinite number of these.
- The whole numbers: 0, 1, 2, 3, etc. These are the same as the countables, but they also include zero.
- The integers: …, -3, -2, -1, 0, 1, 2, 3, etc. It may not seem like much, but the recognition that we can have negative numbers was a huge one, and that there can be just as many negative ones as there are positive ones. This includes all of the whole numbers as well as their negatives.
- The rationals: any number that can be expressed as a fraction of one integer over another. This includes all of the integers (which can be expressed as themselves over one) as well as an infinite number of rationals between every integer. Any infinitely repeating decimal can be expressed as a rational number.
- The reals: includes all of the rationals as well as all of the irrational numbers, such as the square roots of non-perfect squares, π, and a whole host of others. The sum of any rational number and any irrational number will be irrational, but the sums of two irrationals may be rational.
But, while the square root of a positive number is real, the square root of a negative number isn’t well defined.

At least, it wasn’t, until we defined them, and invented the imaginary numbers to do exactly that! An imaginary number is just like a real one, except it’s multiplied by “i”, or the square root of (-1). Numbers can also be complex, where they have both a real part (a) and an imaginary part (b), and are normally expressed as (a + bi).
Now that you know what they are, here are my top 5 fun facts about imaginary numbers!
1.) The square root of i has both real and imaginary parts. The square root of a negative real number is purely imaginary, but the square root of a purely imaginary number has to have both real and imaginary parts! Here’s how you can prove it to yourself. You need for some number, squared, to equal √(-1). Imagine that it could have a real part, x, and an imaginary part, y, so that we could write it as (x + yi). Then we could figure out what x and y need to be for this to work.
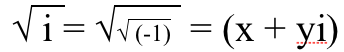
So we square both sides,
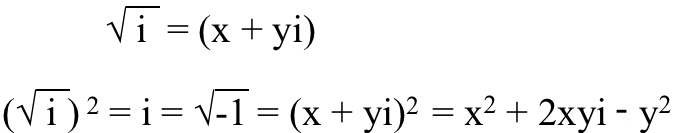
and now we match up the real part with the real part, and the imaginary part with the imaginary part.
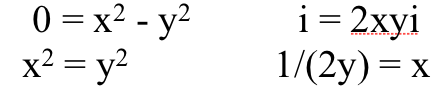
From these two equations, we plug “x” from the right-hand equation into the left,
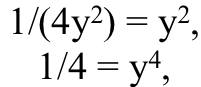
and therefore, we can solve for y:
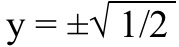
As you can see, there are two possible solutions, and if we use the right-hand (imaginary part) of the equation to solve for x (which turns out to equal y in both cases), we get the two solutions:
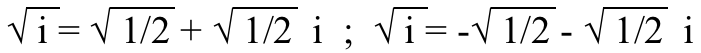
Which brings us to the next fun fact…
2.) Any root of i has multiple unique solutions, and the N-th root has N unique solutions. For positive, real numbers, taking the square root (i.e., the second root) of that number gives you two possible solutions: a positive one and a negative one. For example, √(1) can be +1, or it can be -1, since either one squared will give you 1.
But for i, or √(-1), if you want to take roots of that, you have to make a polynomial equation, like we did above. The thing is, the order of the polynomial equation is dependent on what root we take of it. So the third, fourth, and fifth roots of i have to satisfy:
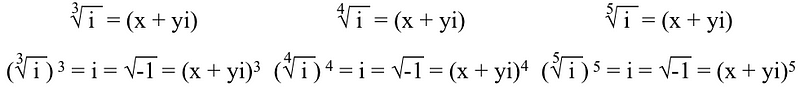
And there will be three, four, and five unique solutions (respectively) for each of the x’s and y’s in these equations. For example, the three solutions for the cubed (3rd) root of i are:
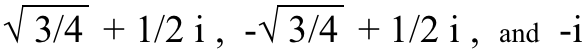
(Try cubing all of these, and see for yourself!) And that’s not even dealing with fractions, which are a whole other can of worms. In fact…
3.) In an imaginary fraction, it actually matters whether the numerator or denominator has the “i” in it. If you think of the number (-1), it doesn’t matter whether you think of it, in fractional terms, as (-1)/1 or as 1/(-1); it’s still the number (-1) either way. But that’s not the case for i! Let me ask you this: what do you think this fraction is?
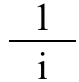
Looking at it, you might think it’s just equal to i, but it’s actually –i!
Want to prove it? Just multiply top and bottom by i, and see for yourself:
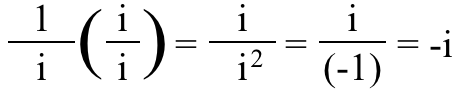
The thing you have to be very careful about is that when you combine or separate square roots of negative numbers, there are intricate rules you must follow to get it correct. Violate them, and you can do all sorts of insane things, like prove that +1 and -1 are equal to one another.
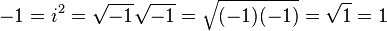
Instead, the underlying math behind how to combine them shows us a really bizarre thing…
4.) e, π, and i are all related to one another. You know that if you have your standard x-and-y axes (both real), you can also represent that coordinate space by polar coordinates, where you have a radial coordinate (r) and a polar angle (θ), like so:
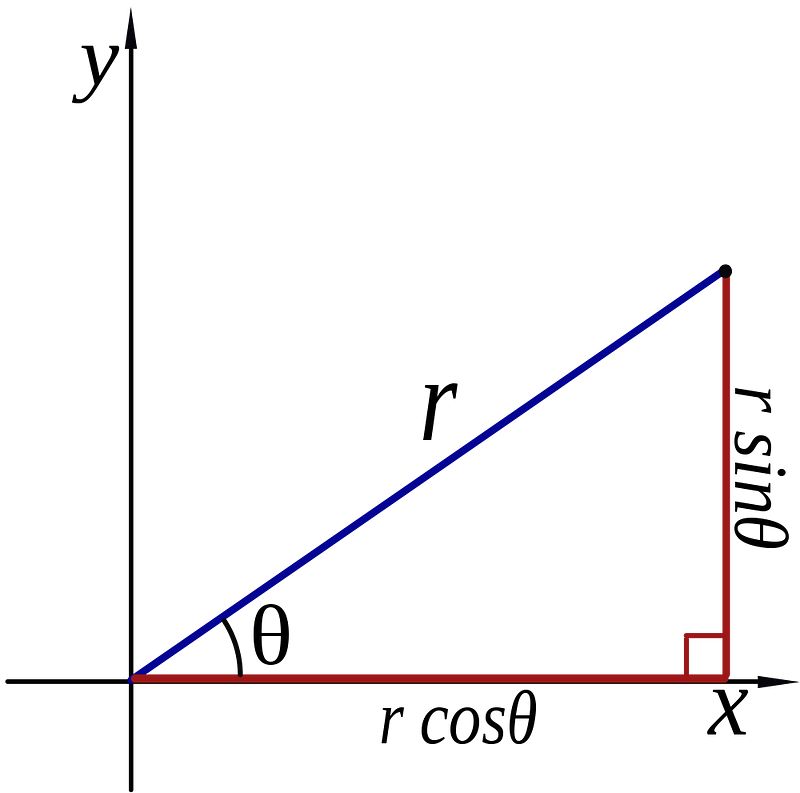
Well, if you create, instead of an x-and-y axis, a real and imaginary axis, you can do the same thing, except this time the angle θ takes you from the real plane into the imaginary plane and back again!
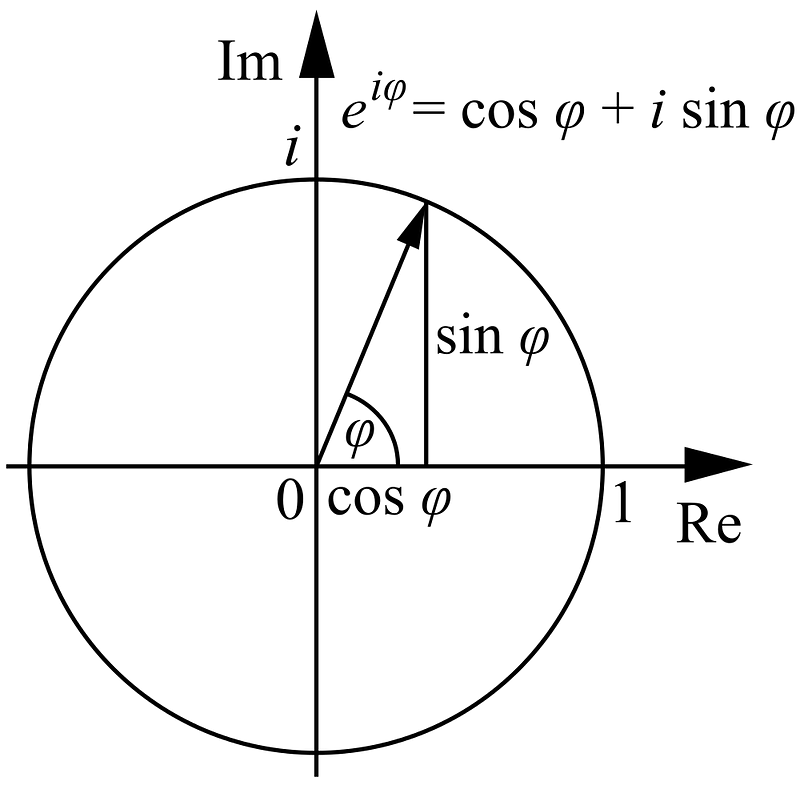
The amazing thing about this is that if we navigate to the position of -1 on the real axis, we arrive at a beautiful identity:
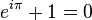
There it is: a simple and unexpected relation between e, i, and π. These relations show up a lot in complex analysis. And yet, if you’re willing to consider exponentials, this last one is a doozy…
5.) i^i, or i raised to the i power, is 100% real. Think about the equation in the image above — Euler’s formula — but instead of heading to (-1) on the real axis, let’s head to i on the imaginary axis instead. In this case, we’d get the equation that:
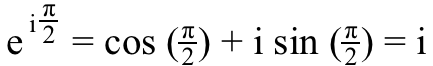
Well, if we want to know what i^i is, all we need to do is raise both sides of this equation to the i power,
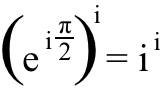
and remember that i^2 = -1, and we find that:
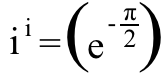
which is about ~0.20788, a purely real number. And those are my top 5 fun mathematical facts about imaginary numbers!
Have one you’d like to share, or a comment on any of these? Head on over to the Starts With a Bang forum on Scienceblogs and weigh in!





