We can’t avoid a singularity inside every black hole

- According to General Relativity, inside of a black hole, there must be a region of infinite density at its center: commonly referred to as a singularity.
- But singularities are pathological in mathematical terms: it’s as though you divided by zero, and everything becomes ill-defined.
- Nevertheless, there are some very compelling reasons, fundamental to physics itself, to think that a singularity is unavoidable inside these monsters. There may be no way out.
It’s easy to think about the idea of a singularity and dismiss it. After all, everything that we know of in physics, at a fundamental level, comes in quantized little bits: particles and antiparticles with a fixed, finite amount of energy inherent to each of them. No matter what tricks you use, there are certain quantum properties that are always conserved and can never be created or destroyed, not in any interaction that’s ever been observed, measured, or even computed. Things like electric charge, momentum, angular momentum, and energy are always conserved, in all circumstances, as are numerous other properties.
And yet, inside of a black hole, the math of General Relativity is very clear: all of that matter and energy that goes into forming it, no matter how it’s initially configured, is going to wind up collapsed down to either a single, zero-dimensional point (if there’s no net angular momentum) or stretched out into an infinitely thin one-dimensional ring (if there is “spin,” or angular momentum, present). Comedian Steven Wright even jokingly said, “Black holes are where God divided by zero,” and in some sense, that’s true.
While many hope that quantum gravity will save us from the inevitability of a singularity, many don’t think that even that is possible, for very good reasons. Here’s why a singularity at the center of every black hole may be completely unavoidable.
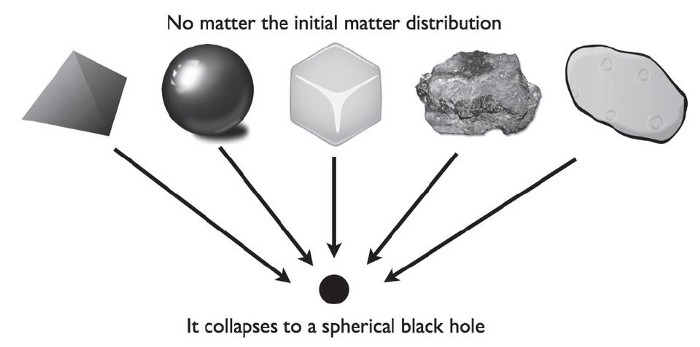
In principle, as Einstein first realized, if all you have is some configuration of matter that starts off distributed over some volume (with no rotation or initial motions), the outcome is always the same: gravitational attraction will bring all of that matter together until it collapses down to a single point. Around that point, dependent on how much mass/energy there is all together, there will form a region of space known as an event horizon: a volume from within which the escape velocity, or the speed you’d need to travel to escape from this object’s gravitational pull, would be greater than the speed of light.
That “solution” to Einstein’s equation was first worked out in detail by Karl Schwarzschild, and represents the configuration known as a non-rotating (or Schwarzschild) black hole. For many years, astronomers and physicists alike wondered if these objects were just mathematical oddities and perhaps even pathologies predicted by General Relativity, or whether these corresponded to real objects that were out there somewhere within this Universe.
The story began to change in the 1950s and 1960s with the work of Nobel Laureate Roger Penrose, whose pioneering work demonstrated how black holes (and their event horizons) could form from an initial configuration that didn’t have one earlier. This was the work that Penrose, quite deservingly, was awarded the Nobel Prize for, and it kicked off a proverbial firestorm of black hole research.

If black holes could realistically form within our Universe, then that means we should be able to do two things with them.
- We should be able to calculate under which physical circumstances they can form, and hence, where we expect to find them and what signatures they ought to give off.
- And then, we should be able to actually go out and find them, detect their signatures, and even measure fundamental properties about them if our technology ever reaches that point.
For the first one, all you really need is enough mass concentrated within a given volume of space. This could occur because you have a collection of matter that’s of relatively low density, but that occupies enough space so that when you look at it as a whole, it must inevitably collapse to a central singularity: a direct collapse black hole. You can also have a black hole arise from the implosion of the core of a massive enough star: in a core-collapse supernova, for instance, where the core is massive enough to collapse to a black hole. Or, you could have multiple massive and dense objects, like stellar remnants such as neutron stars, merge together and cross a critical mass threshold, where they’ll become a black hole. These are three of the most common ways that the Universe could actually create a black hole.
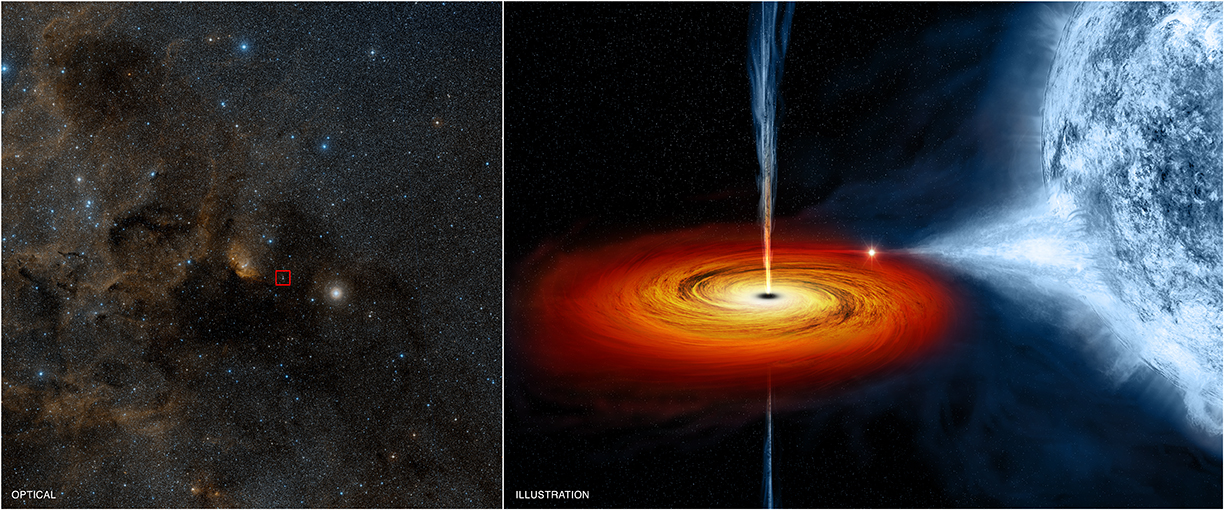
Over on the observational side, there are many different signatures that a black hole gives off. If a black hole is a member of a binary system, where another star orbits it from afar, then we can see the star “move” in a helix-like shape as it moves through the galaxy, revealing the black hole’s presence from gravity alone. If it’s at the center of a galaxy, we can see other stars orbit it directly. If there’s a close-in stellar companion to a black hole, then the black hole could be capable of “stealing” or siphoning mass from the companion onto itself, and much of that mass will be heated, accelerated, and shot out in X-ray emitting jets. The first black hole ever detected, Cygnus X-1, was found from exactly this X-ray emission.
We can also detect what effects black holes have on their surrounding matter. They develop accretion disks with flows within them, flaring when these flows get accelerated and shot out in bi-directional jets. They can tidally disrupt any stars or planets or gas clouds that get too close to them, creating cataclysmic signatures when they do so. They can inspiral and merge together, creating gravitational wave signatures that we can directly detect, and have done so many dozens of times since 2015.
And, perhaps most famously, they bend the light from background sources that are behind them, creating an image of the vaunted event horizon of a black hole itself that can be detected in radio wavelengths of light.
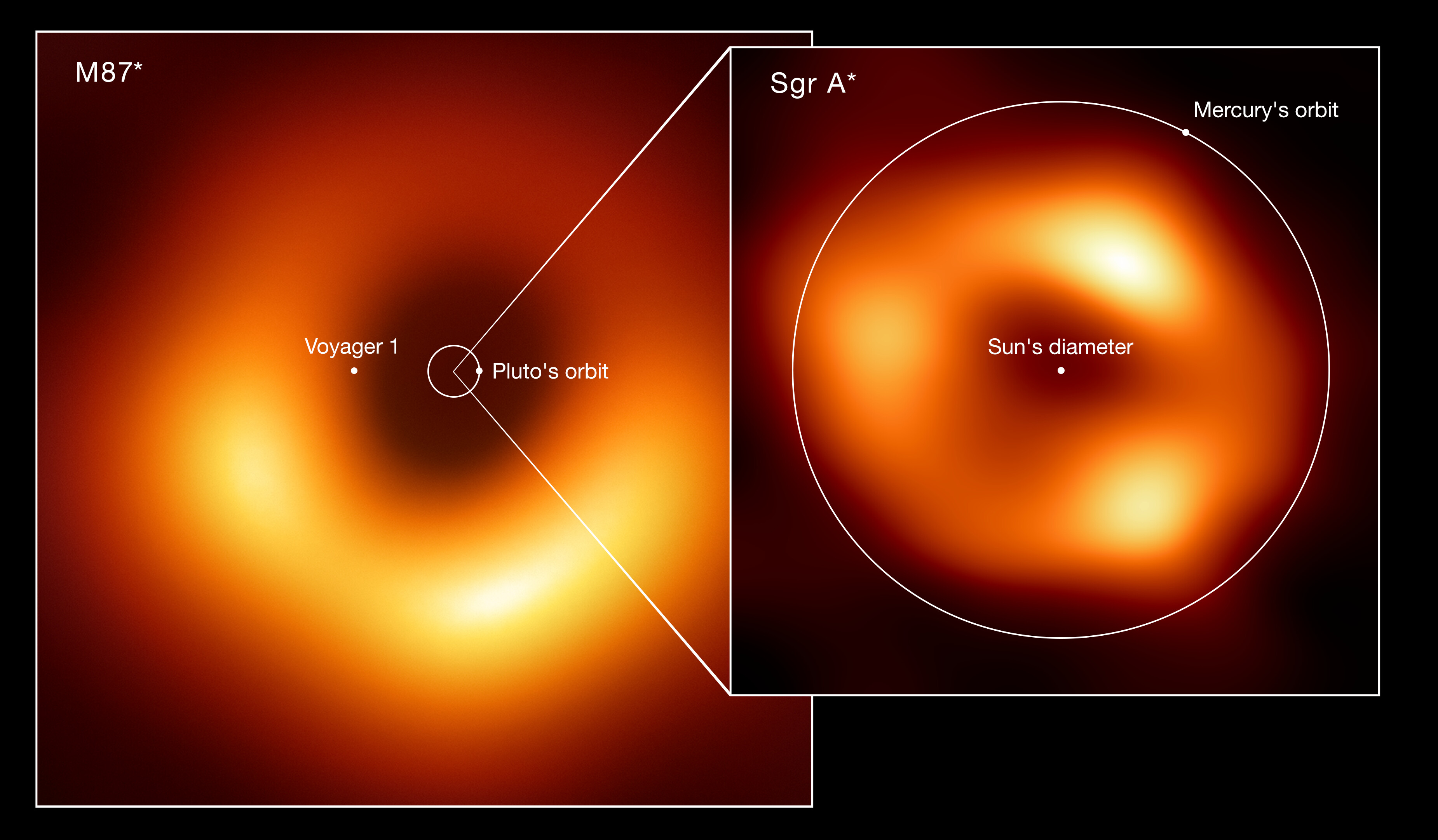
From everything we’ve learned from a theoretical and observational perspective, we can not only conclude that black holes should and do exist, but we’ve measured their properties, confirming a lower mass limit for them of around three solar masses. Additionally, we’ve measured their event horizons directly, and confirmed that they have the properties, sizes, gravitational wave emissions, and light-bending features that are extremely consistent with what General Relativity predicts. Black holes, for as much as we can say so about anything in the Universe, really do exist.
But what’s going on inside of their event horizons?
This is something that no observation can tell us, unfortunately. It’s only the things that occur outside of the event horizon — where the escape velocity of signals are below the speed of light — that can ever reach us in our location. Once something crosses over to the inside of the event horizon, there are only three properties that can be measured from outside:
- the mass,
- electric charge,
- and total angular momentum,
of the black hole. That’s it. Astrophysicists sometimes refer to these three properties as the type of “hair” a black hole can have, with all other properties getting eliminated as a consequence of the famous no-hair theorem for black holes.
But there’s a tremendous amount to be learned by looking at the differences between an “almost” black hole and an actual black hole.
A white dwarf, for example, is a dense collection of atoms, often greater in mass than the Sun but smaller in volume than the Earth. Inside, at its core, the only reason it doesn’t collapse is because of the Pauli Exclusion Principle: a quantum rule that prevents any two identical fermions (in this case, electrons) from occupying the same quantum state in the same region of space. This creates a pressure — an inherently quantum “degeneracy pressure” — that prevents the electrons from getting close beyond a certain point, which holds the star up against gravitational collapse.
Similarly, an even denser neutron star is a collection of neutrons — or in an even more extreme scenario, a quark-gluon plasma that may involve quarks beyond the lowest-energy up-and-down species — held together by the Pauli degeneracy pressure between their particle constituents.
But in all of these cases, there’s a mass limit to how massive these objects can get before gravity becomes irresistible, collapsing these objects down to a central singularity if a thermonuclear reaction doesn’t destroy the object entirely in the lead-up to the creation of an event horizon.
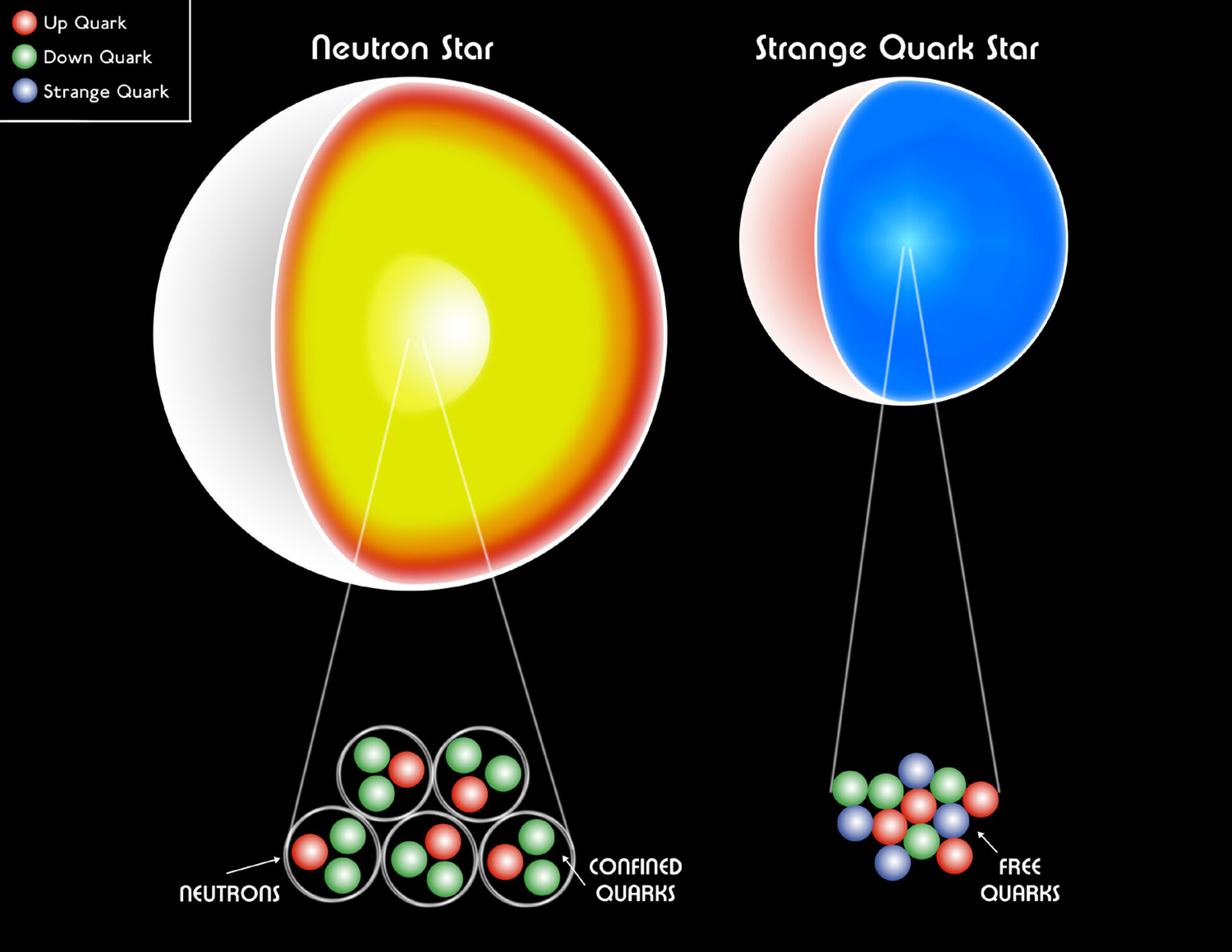
Many have wondered, however, if there couldn’t be something inside an event horizon that was static, stable, and of a finite volume: holding itself up against complete collapse down to a singularity the same way that a white dwarf or neutron star holds itself up against collapsing further. Many contend that there could be some sort of exotic form of matter inside an event horizon that doesn’t go to a singularity, and that we simply have no way of knowing whether this occurs or not without being able to access the information inside a black hole.
That argument, however, falls apart on physical grounds. We can see this by asking-and-answering a very specific question that illuminates a key feature that ultimately leads to an inescapable conclusion: the presence of a singularity within a black hole’s event horizon. That question is, simply, as follows:
“What’s the difference, then, between something that doesn’t collapse down to a central singularity, forming an event horizon along the way, and something that does?”

The outermore material is always being drawn in by gravity; in General Relativity, remember that it isn’t just that masses move through space, but that space itself is compelled to “flow,” as illustrated above, as though it’s moving like a river’s current or a moving walkway, and that particles can only move through space-and-time relative to the underlying motion of space itself. But in order for all the masses in this spacetime to not get drawn into a central singularity, something must be resisting that motion, and exerting an “outward” force to counteract that inward motion that gravitation is attempting to induce.
The key is to take on a particle physics perspective here: think about what sort of force the “innermore” part of the object has to exert on the “outermore” part. Whether:
- a quantum force like the strong nuclear, weak nuclear, or electromagnetic force,
- a classical force like General Relativity,
- an inherently quantum effect like Pauli degeneracy pressure,
- or a novel quantum force like some yet-to-be-discovered quantum theory of gravity,
there’s a limit to how fast any of these effects can propagate outward: the speed of light. These forces all have a maximum speed at which they can travel, and that speed is never greater than the speed of light.
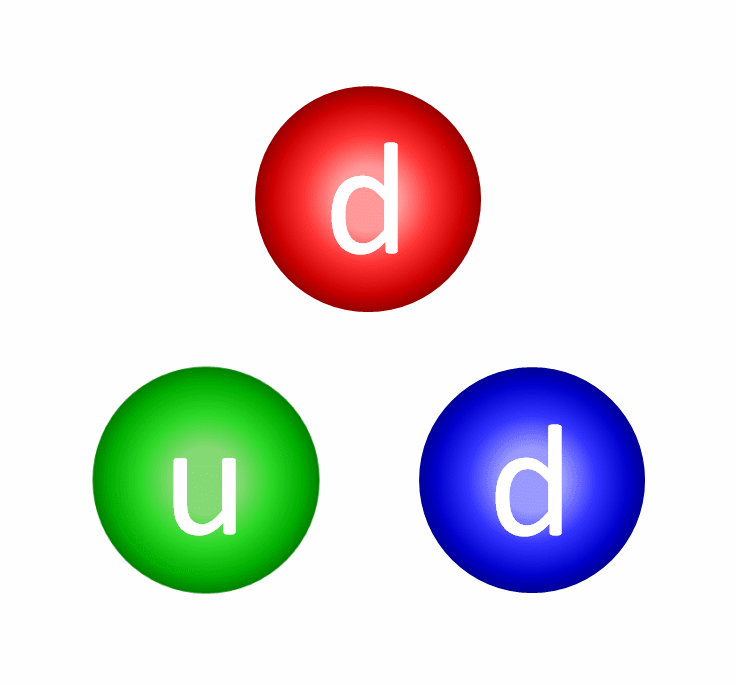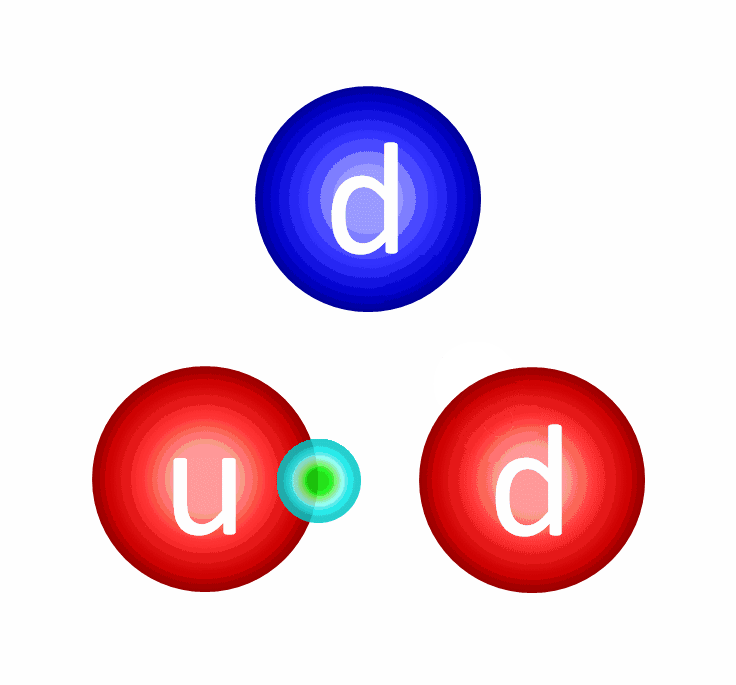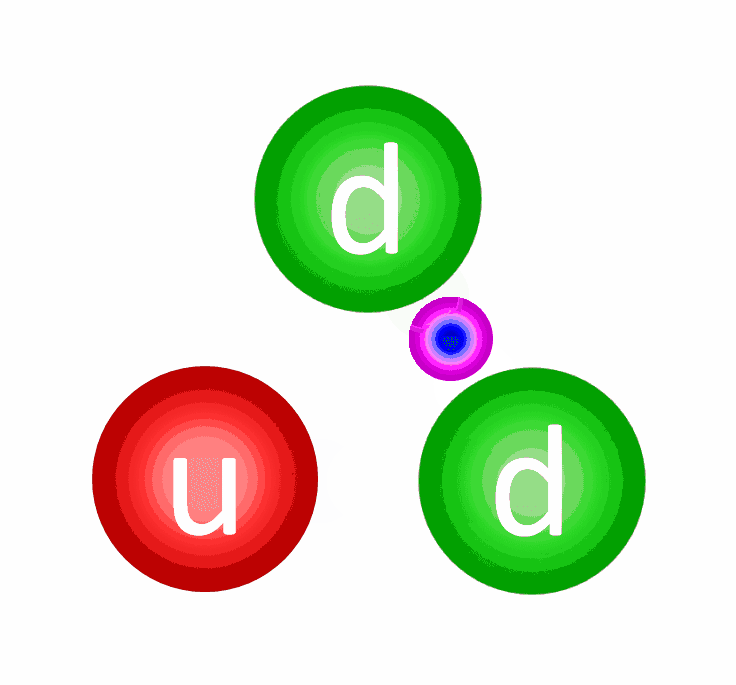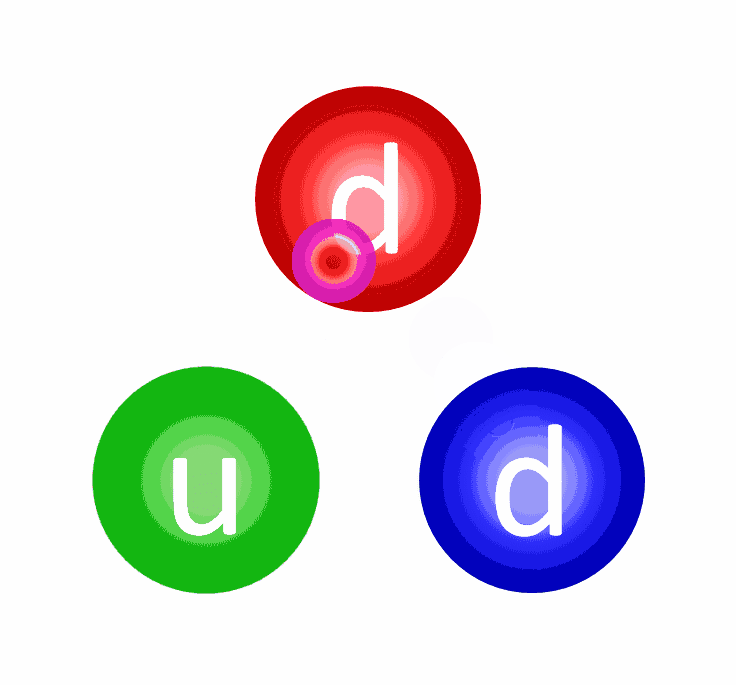
And that’s where the big problem arises! If you create an event horizon, then from within that region of space, any attempt from an innermore component to exert a force on an outermore component will run into a fundamental problem: that if your force-carrying signal is limited by the speed of light, then in the time that passes from:
- when the innermore particle emits the force-carrier,
- the force carrier travels to the outermore particle,
- and the outermore particle absorbs it,
we can calculate how that system of the innermore particle, the outermore particle, and the force carrier exchanged between them evolves.
The lesson you learn applies to all systems that are limited by the speed of light, and it’s astounding: by the time the “outermore” particle absorbs the force-carrying particle exchanged between it and the “innermore” particle, the initially outermore particle is now closer to the central singularity than the initially innermore particle was when it first emitted the force-carrier.
In other words, even at the speed of light, there is no force that one particle can exert on another from inside the event horizon to prevent its inevitable fall into the central singularity. Only if some sort of superluminal (i.e., tachyonic) phenomenon exists inside an event horizon can a central singularity be prevented.
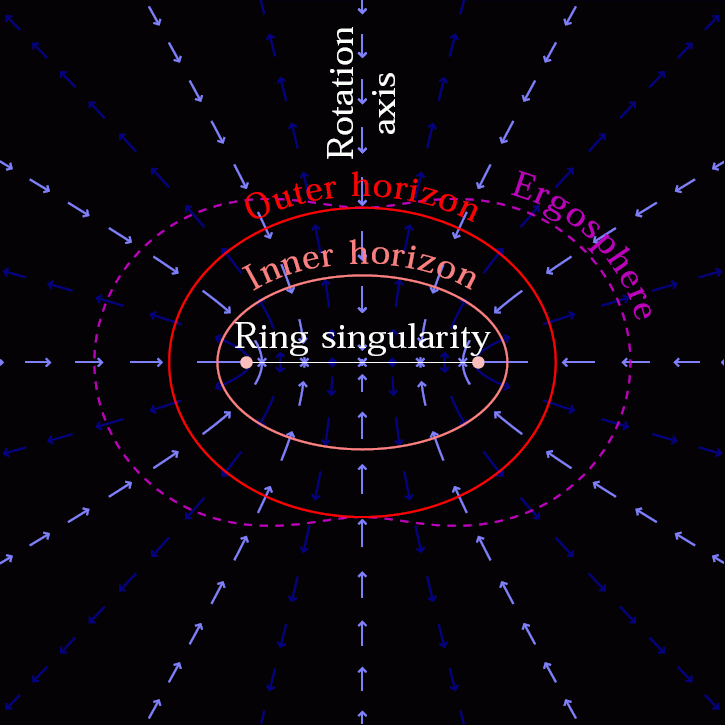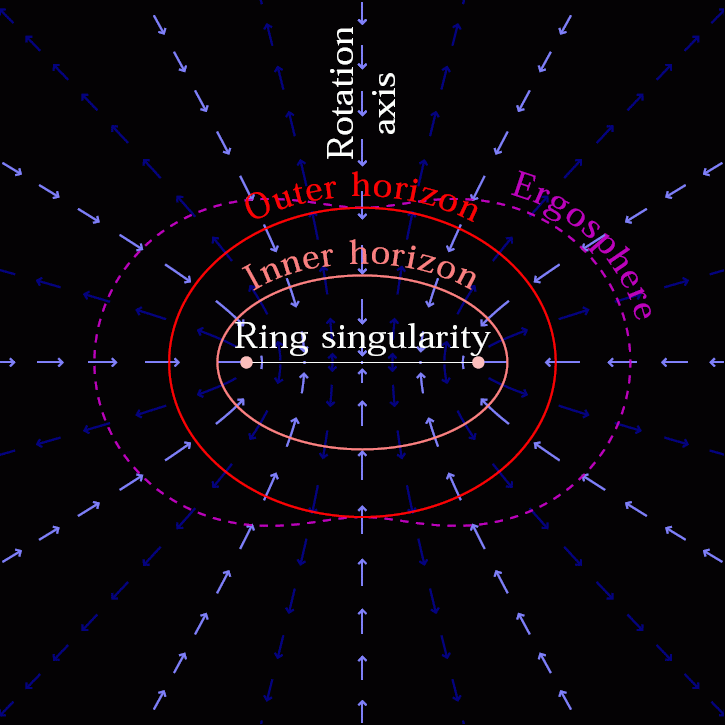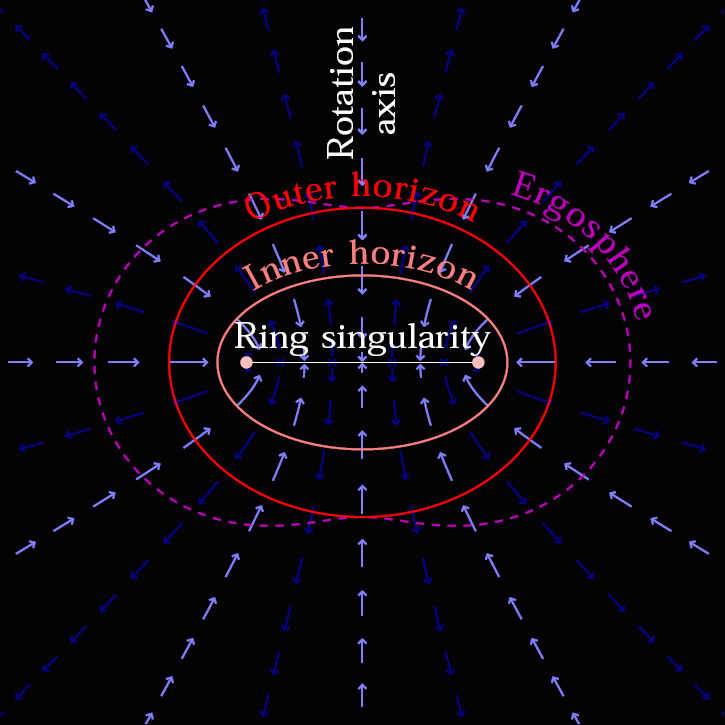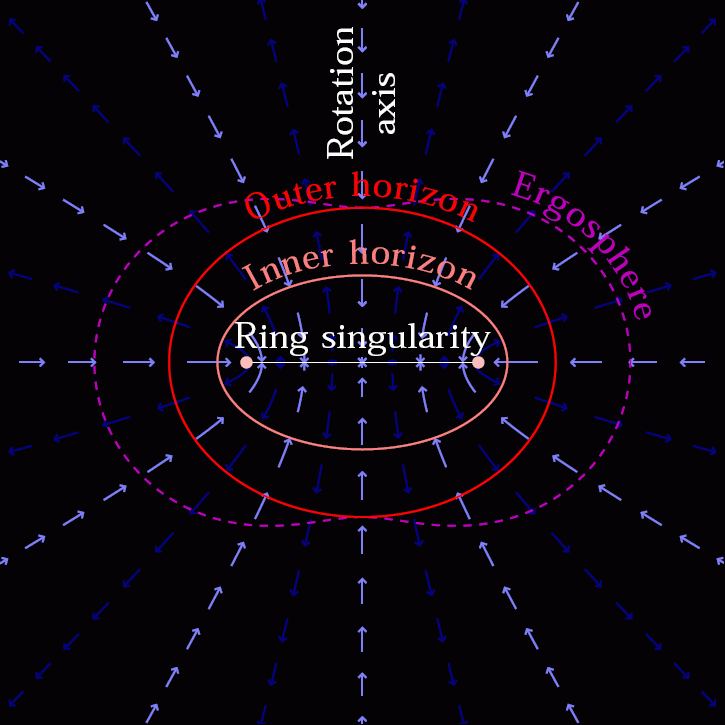
What’s so powerful about this analysis is that it doesn’t really matter what sort of quantum theory of gravity exists at a more fundamental level than General Relativity: as long as the speed of light is still the speed limit of the Universe, there’s no “structure” one can make out of quantum particles that won’t result in a singularity. You’ll still arrive at a zero-dimensional point if you fall into a non-rotating black hole, and you’ll still be drawn in toward a one-dimensional ring if you fall into a rotating black hole.
However, it is possible that these black holes are actually gateways to a baby Universe that resides within them; although whatever falls in would be reduced to pure energy (with the caveat that there may be quantum quantities that are still conserved, and E = mc² would still apply), with no evidence existing in our Universe, outside the event horizon, for any exotic behavior that happened to the infalling particle(s) on the other side.
From our perspective outside an event horizon, and from the perspective of any particle that crosses over to the inside of an event horizon, there’s simply no way to escape it: in a finite and relatively short amount of time, any infalling matter must wind up at a central singularity. Although the physics that we know of does indeed break down and only gives nonsensical predictions at the singularity itself, the existence of a singularity truly cannot be avoided unless some wild, exotic, new physics (for which there is no evidence) is invoked. Inside a black hole, a singularity is all but inevitable.





