Do we really have more than three spatial dimensions?

From any point in space, you are free to move in any direction you choose. No matter how you orient yourself, you can travel forward-or-backward, up-and-down, or side-to-side: you have three independent dimensions that you can navigate. There is a fourth dimension: time; we move through that just as inevitably as we move through space, and via the rules of Einstein’s relativity, our motion through space and time are inextricable from one another. But could additional motions be possible? Could there be additional spatial dimensions beyond the three that we know?

This has been a question that physicists have entertained for about a century, and that many mathematicians and philosophers have wondered about for significantly longer. There are numerous compelling reasons to consider the possibility, but there’s also the evidence we have from our Universe: both from a mathematical point of view and from a purely physical point of view. Although the physical consequences that would arise from extra spatial dimensions have tight constraints on them, the mathematical possibilities are just as mind-expanding as ever.

A visualization of a 3-torus model of space, where our observable Universe could be just a small portion of the overall structure. Similar to imagining our Universe (or any three-dimensional space) being enclosed by a two-dimensional boundary, our three-dimensional space may in fact be the boundary around a higher-dimensional space.

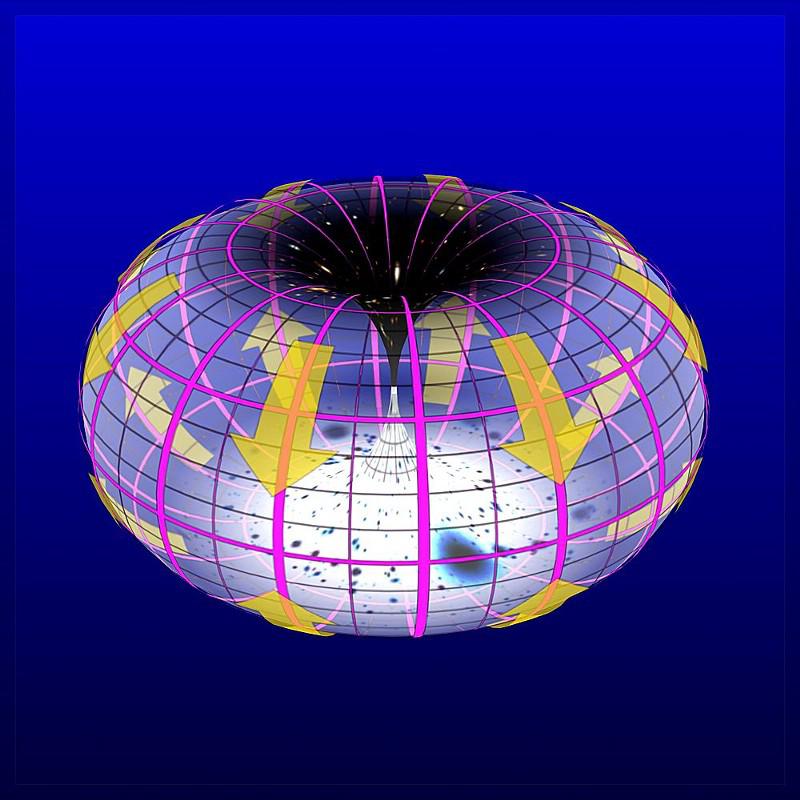
Perhaps the best starting point is to consider what life would be like if you, a three-dimensional being, were to encounter someone who lived in a two-dimensional Universe, as though they were confined to living on the surface of a sheet of paper. They would be able to move forward-or-backward as well as side-to-side, but they would have no concept of up-and-down. To them, it would be like asking “What’s north of the North Pole?” here on Earth; it’s a question that just doesn’t make sense.

But to a three-dimensional being, “up-and-down” are obvious. We can take any of these surface-dwellers and:

• lift them up off of their surface,
• reach into their insides and manipulate them without having to cut into them,
• teleport them from one location to another by moving them through the third dimension,
• or even to move ourselves down onto their surface, interacting with them with a cross-section of our own bodies.

The fact that they cannot perceive this extra, third dimension is not necessarily an argument against its existence.

What we can constrain, though, is what the properties of such an extra dimension can (or cannot) possess. For example, if a being living on that two-dimensional surface spoke, how would the sound waves that they emitted travel and spread out? Would they remain confined to the two-dimensional Universe, or would they leak out into the three-dimensional Universe? If you were a three-dimensional observer watching these flatlanders go about their business, would you be able to overhear their conversations from outside their two-dimensional surface, or would the sound fail to travel through this third dimension?

You can figure this out even if you’re a two-dimensional creature bound to living on that flat, two-dimensional surface. If you listen to an identically generated sound from a variety of different distances, you can measure how loud that arriving signal sounds to you, and that allows you to determine how the sound is spreading out. Is it spreading out like a circle, where its energy is confined to just two dimensions? Is it spreading out like a sphere, diluting across three dimensions?

The brightness distance relationship, and how the flux from a light source falls off as one over the distance squared. A satellite that’s twice as far away from Earth as another will appear only one quarter as bright, but the light-travel time will be doubled and the amount of data throughput will also be quartered. Gravitation, light, sound, and electromagnetism all fall off as the inverse distance squared.

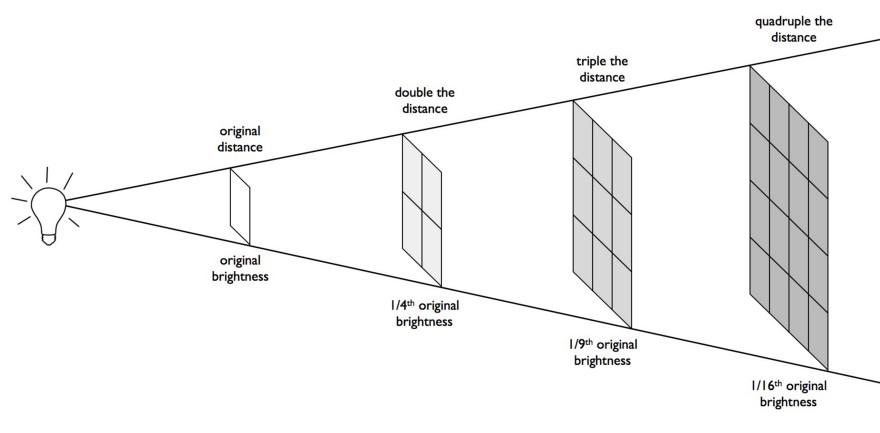
In three spatial dimensions, signals like the intensity of sound, the flux of light, even the strength of the gravitational and electromagnetic forces, they all fall off as one over the distance squared: spreading out like the surface of a sphere. This information tells us two compelling pieces of information about the number of dimensions in the Universe.

1. If there are large extra dimensions — dimensions that are macroscopic in some sense — the forces and phenomena in our Universe don’t “leak” into them. Somehow, the particles and interactions that we know of are confined to our 3 space (and 1 time) dimensions; if there are extra dimensions of any sort of appreciable size, they do not have observable effects on the particles that we observe.
2. Alternatively, there could be very small extra dimensions, and the effects of various forces, particles, or interactions could show up on those very small scales: with forces spreading out as one over the distance cubed (for four spatial dimensions) or even to some higher power.

In the case of very small extra dimensions, this is something we can test.

The collision of two particles can result in charged components getting very close, enabling us to test the nature of various force laws. When two protons collide, it isn’t just the quarks making them up that can collide, but the sea quarks, gluons, and beyond that, field interactions. All can provide insights into the spin of the individual components, and allow us to create potentially new particles if high enough energies and luminosities are reached.

For example, by bringing two charged particles extremely close together, we can measure the attractive or repulsive forces between them. In particle accelerators, like the Large Hadron Collider at CERN, we can collide charged particles with one another at tremendous energies, getting them down to separation distances on the order of ~10^-18 meters or so. If there were deviations from the expected behavior of the electromagnetic force at these energies, our precision experiments would have revealed it. For the strong, weak, and electromagnetic forces, there is no evidence for extra dimensions down to these exquisite precisions.

But for gravitation, it’s much more difficult. Because gravity is so mind-bogglingly weak, it’s a challenge to measure the force of gravity on even modestly small scales. In recent years, they’ve gotten down to testing gravity below the ~1 millimeter scale, down to micron-level scales. The results, excitingly, show that gravity doesn’t “leak” into extra dimensions down to any observable scales, but there’s still a long way to go.

This image, of an optically levitated microsphere in a vacuum, provides a laboratory for testing gravitation and the nature of the inverse-square force law down to ~micron scales. Despite the variety of enormously precise experiments, no deviations, which could indicate the presence of extra dimensions, have ever been found.

In principle, there are no constraints on having very small extra dimensions below our experimental constraints. Numerous scenarios — warped extra dimensions, flat extra dimensions, extra dimensions that only affect gravitation, etc. — are very difficult to rule out; the only superior constraints we could hope for are either to build a larger, more powerful collider, or to harness cosmic rays for precision purposes. Until those arise, we have to admit that, from scales of about ~10^-19 meters all the way down to the Planck scale at ~10^-35 meters, we could have one or more extra spatial dimensions, and we have no tests that have constrained those possibilities.

In fact, this is largely what string theory hypothesizes: that there’s not just one extra spatial dimension, but many of them — perhaps six — that are below the experimental limits of detection. It is, of course, eminently possible for extra dimensions to exist, they simply are compelled to be very small. If this were the case, there would be no way of knowing it right now, but with future experiments that were more powerful, we could, perhaps, uncover them. We might even learn of their existence via new particles inherent to these extra dimensions: Kaluza-Klein particles.

In theory, there could be more than three spatial dimensions to our Universe, so long as those “extra” dimensions are below a certain critical size that our experiments have already probed. There is a range of sizes in between ~10^-19 and 10^-35 meters that are still allowed for a fourth (or more) spatial dimension, but nothing that physically occurs in the Universe can be allowed to rely on that fifth dimension.

Even without resorting to exotic field theories with many new parameters, extra dimensions could exist within the context of relativity alone. About 40 years ago, two physicists who specialized in General Relativity — Alan Chodos and Steve Detweiler — wrote a paper demonstrating how our Universe could have arisen from a five-dimensional Universe: with one time and four spatial dimensions.

What they did was take one of the exact solutions in General Relativity, the Kasner metric, and apply it to the case of having an extra dimension: four spatial ones instead of three. In the Kasner metric, space cannot expand isotropically (the same in all directions), which is the Universe we clearly have.

So why would we consider it? Because, as they showed, it has the properties that one of the dimensions will contract over time, getting smaller and smaller until it’s below any threshold we care to observe. When that occurs — i.e., when that one particular spatial dimension is small enough — the remaining three spatial dimensions don’t just appear isotropic, but also homogeneous: the same everywhere. In other words, by starting with four spatial dimensions and allowing one to contract, you can get a Universe that looks remarkably like ours out. The paper had the lovely title, “Where has the fifth dimension gone?”

The first paper to ever show that an additional dimension could have existed in the early Universe and be imperceptible today was by Chodos and Detweiler in 1980.

There is one other possibility for where extra dimensions could be, and it goes back very much to the original scenario we envisioned: us, as three-dimensional beings, with access to beings that were confined to a two-dimensional sheet. Only, this time, we’re the sheet: we’re confined to accessing three spatial dimensions, but that those three dimensions serve as a boundary for a larger, higher-dimensional space.

An example of this would be something like a hypersphere or a hypertorus: a four-dimensional space, but with a three-dimensional boundary. That boundary would represent our Universe that we know and can access, but there would also be at least one additional dimension that we cannot see, feel, or access, but is still very much a part of the Universe.

This idea, sometimes known as the holographic Universe, possesses a number of compelling, interesting features. Some problems in physics that are very difficult to solve in three spatial dimensions, like the Wess-Zumino model, become practically trivial when you add in one extra dimension, which is what string theorist Ed Witten did, and is why the model is known today as the Wess-Zumino-Witten model.

The idea that the forces, particles and interactions that we see today are all manifestations of a single, overarching theory is an attractive one, requiring extra dimensions and lots of new particles and interactions. Many such mathematical constructs exist to explore, but without a physical Universe to compare it to, we’re unlikely to learn anything meaningful about our Universe.

Moreover, the holographic principle has a strong piece of mathematical evidence for it: if you take a five-dimensional anti-de Sitter spacetime, it turns out to be completely equivalent to a four-dimensional conformal field theory. In physics, this is known as the AdS/CFT correspondence, and it related certain string theories in higher dimensions to certain quantum field theories that we’re familiar with in our three-space and one-time dimensions. The conjecture was first proposed in 1997 by Juan Maldacena, and since that time it has become the most-cited paper in high-energy physics history, with over 20,000 citations.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

But despite the power and promise of this theoretical framework, both on small scales and to potentially help us solve very difficult problems that plague physics in our limited three spatial dimensions, we have no direct evidence that points to the existence of these extra dimensions at all. If they were to exist, they would open up a whole new Universe of physical possibilities, and it would certainly pave the way for a new holy grail of physics: to harness and access these additional dimensions. But without evidence, their existence is purely speculative at this point.

This photograph of a hologram at the MIT museum looks like a three-dimensional object, but is only a two-dimensional light field encoded onto the surface of a hologram. Holograms are lower-dimensional surfaces that encode information about the entire higher-dimensional object within the higher-dimensional space. The idea of the holographic principle is that our Universe and the quantum field theoretical laws that describe it is the surface of a higher-dimensional spacetime that includes quantum gravity.

So, how many dimensions are there in our Universe? From the direct evidence we have, there are three spatial dimensions and one time dimension, and no more are required to solve any problems or explain any phenomenon we’ve ever observed. But the possibility that extra dimensions exist remains tantalizing, because if they did exist, they could explain a great number of mysteries that exist today.

Is there a framework where gravity and the other fundamental forces unify? Perhaps, and at least one of the ones that could work involves extra dimensions. There are many problems that are very difficult to solve in three space and one time dimension, but that simplify greatly with one or more extra ones. There are a number of ways to obtain a Universe very much like our own if you start with one or more extra dimensions and a set of very beautiful and elegant pictures that could describe our Universe.

But unless and until we obtain direct evidence that points toward these claims, we have no choice but to consider them as highly speculative. In physics, as in all sciences, it’s evidence, not popularity, that determines what is true about our Universe. Until that evidence arrives, we can remain open to extra spatial dimensions as a possibility, but the only responsible position is to remain skeptical.