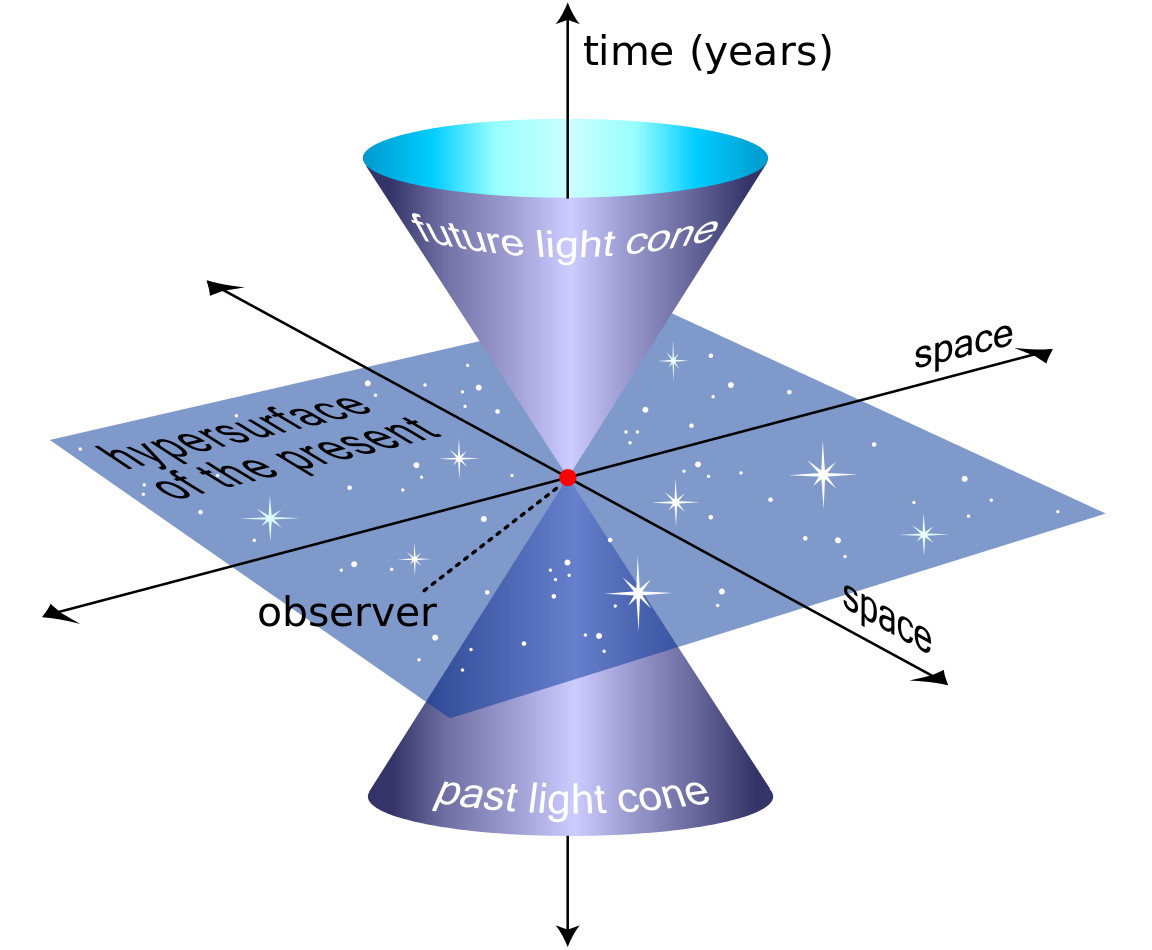
Time isn’t simply just another dimension

- According to Einstein’s General Relativity, matter and energy curve the fabric of spacetime, and that curved spacetime determines the motion of matter and energy.
- But while spacetime itself is four dimensional, it can be decomposed into three spatial dimensions and one time dimension.
- Even though we understand the mathematics governing them magnificently, time has some fundamental differences from every other dimension; here’s what everyone should know.
Here’s a question that most of us have been asked at some point in our lives, “What’s the shortest distance between two points?” By default, most of us will give the same answer that Archimedes gave more than 2,000 years ago: a straight line. If you take a flat sheet of paper and put two points down on it absolutely anywhere, you can connect those two points with any line, curve, or geometrical path you can imagine. So long as the paper remains flat, uncurved, and unbent in any way, the straight line connecting those two points will be the shortest way to connect them.
This is precisely how the three dimensions of space work in our Universe: in flat space, the shortest distance between any two points is a straight line. This is true regardless of how you rotate, orient, or otherwise position those two points. But our Universe isn’t made up merely of three space dimensions, but of four spacetime dimensions. It’s easy to look at that and say, “Oh, well, three of them are space and one of them is time, and that’s where we get spacetime,” and that’s true, but not the full story. After all, the shortest distance between two spacetime events isn’t a straight line any longer. Here’s the science of why.
For most of us, our first exposure to the idea of a straight line being the shortest distance between two points comes from a place we might not realize: the Pythagorean theorem. You might remember the Pythagorean theorem as a rule about right triangles, that if you square each of the short sides and add them together, that equals the square of the long side. In math terms, if the short sides are a and b while the long side is c, then the equation relating them is a² + b² = c².
Think about what this means, however, not from the perspective of pure mathematics alone, but in terms of distances. It means that if you move through one of your spatial dimensions by a certain amount (a, for example) and then move through a perpendicular dimension by another amount (b, for instance), then the distance between where you began and where you wound up is equal to c, as defined by the Pythagorean theorem. In other words, the distance between any two points on a plane, where those points are separated by a in one dimension and b in another dimension, is c, where c = √(a² + b²).
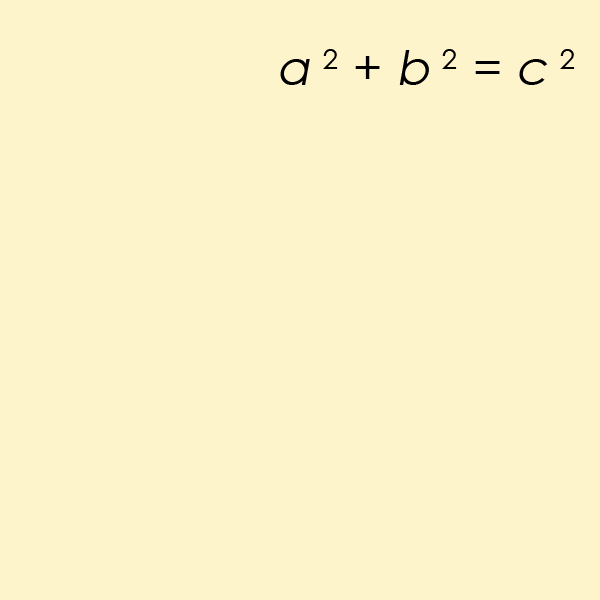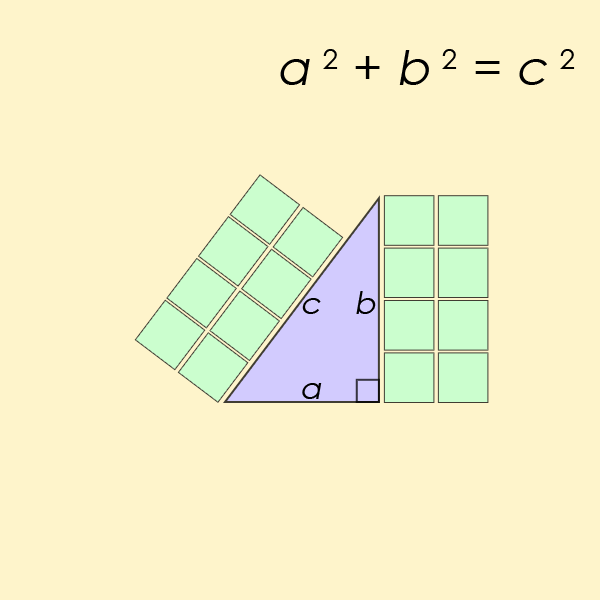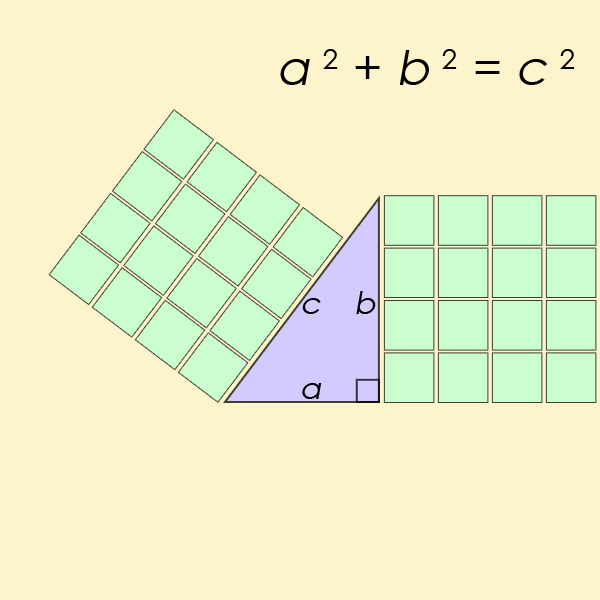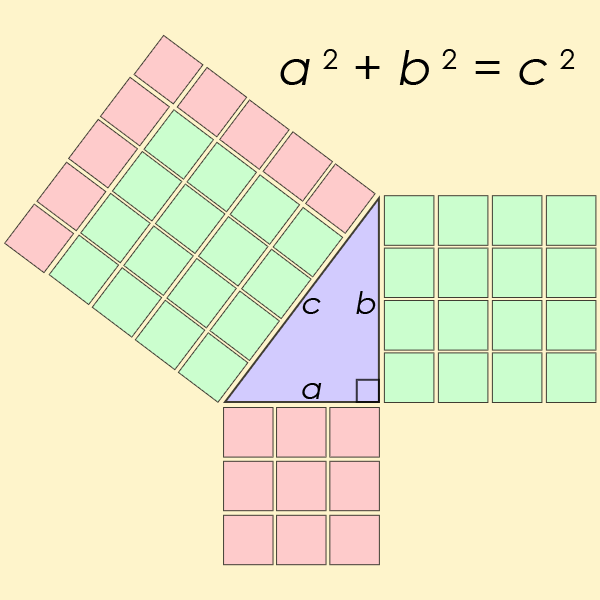
In our Universe, of course, we’re not restricted to living on a flat sheet of paper. We have not just length and width (or the x and y directions, if you prefer) dimensions to our Universe, but depth (or the z direction) as well. If you want to figure out what the distance is between any two points in space, it’s the exact same method as it was in two dimensions, except with one extra dimension thrown in. Whatever amount your two points are separated by in the x direction, the y direction, and the z direction, you can figure out the total distance between them just the same as earlier.
Only, because of the extra dimension, the distance between them — let’s call it d — is going to be given by d = √(x² + y² + z²). This might look like a scary equation, but it just says that the distance between any two points is defined by the straight line connecting them: the line that accounts for the separation between your two points in all three dimensions: the x-direction, the y-direction, and the z-direction combined.
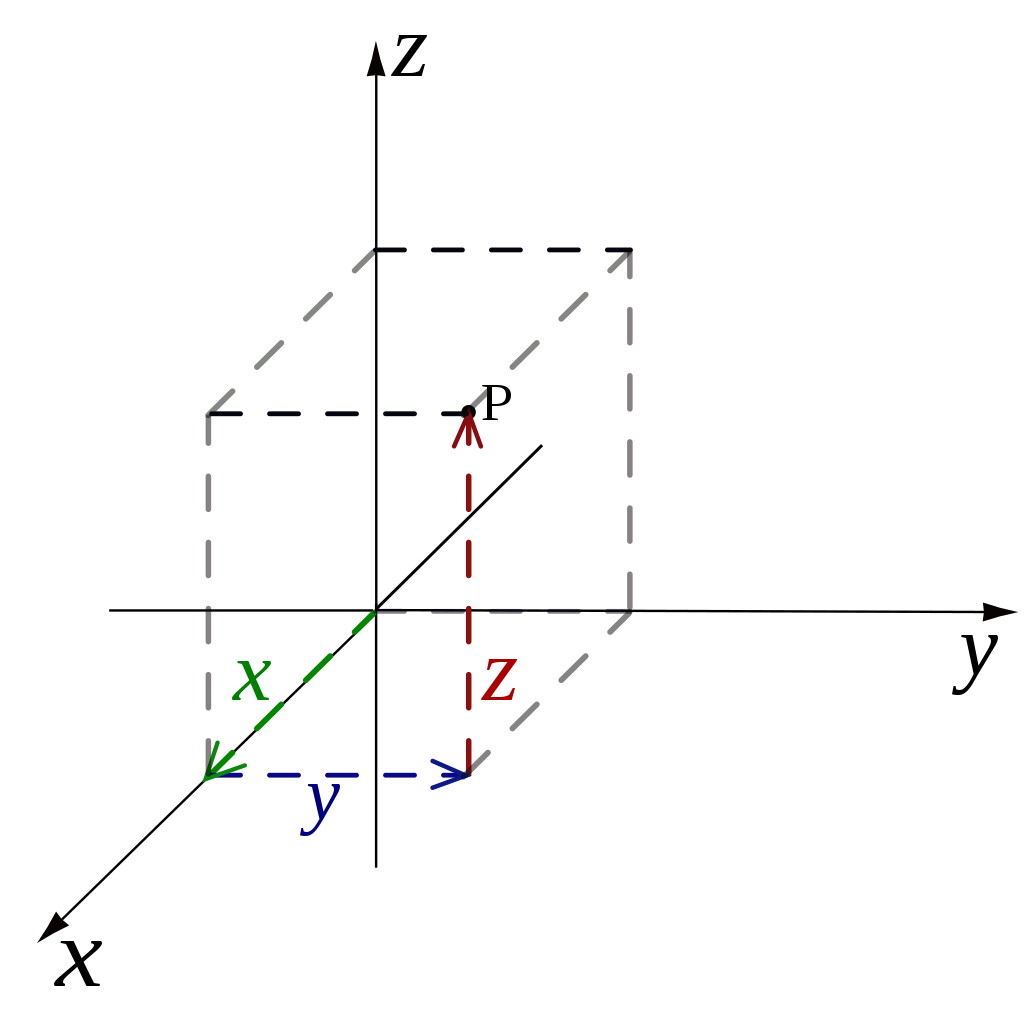
One of the interesting and important realizations about this relationship — the distance between two points being a straight line — is that it absolutely does not matter how you orient your visualization of the x, y, and z dimensions. You can either:
- change your coordinates so that the x, y, and z dimensions are in any (mutually perpendicular) directions you like, or
- rotate these two points by any amount in any direction,
and the distance between them will not change at all.
Sure, the individual components will change if you either rotate your perspective or rotate the line connecting those two points, as your definitions of length, width, and depth will change relative to one another for that line as the rotation occurs. But the overall distance between those two points doesn’t change at all; that quantity of the distance between those points remains what we call “invariant,” or unchanging, regardless of how you rotate them.

Now, let’s not simply consider space, but time as well. You might think, “Well, if time is just a dimension, too, then the distance between any two points in spacetime will work the same way.” For example, if we represent the time dimension as t, you might think the distance would be the straight line connecting two points through the three spatial dimensions as well as the time dimension. In mathematical terms, you might think that the equation for the separation between any two points would look something like d = √(x² + y² + z² + t²).
After all, this is pretty much the same change we made when we went from two dimensions to three dimensions, except this time we’re going from three dimensions to four dimensions. It’s a reasonable step to attempt, and describes exactly what reality would look like if we had four dimensions of space, rather than three.
But we don’t have four dimensions of space; we have three dimensions of space and one dimension of time. And despite what your intuition may have told you, time isn’t “just another dimension.”

There are two ways that time, as a dimension, is different from space. The first way is a small one: you can’t put space (which is a measurement of distance) and time (which is a measurement of, well, time) on the same footing without some way to convert one to the other. Fortunately, one of the great revelations of Einstein’s theory of relativity was that there is an important, fundamental connection between distance and time: the speed of light, or equivalently, of any particle that travels through the Universe without a rest mass.
The speed of light in a vacuum — 299,792,458 meters per second — tells us precisely how to relate our motion through space with our motion through time: by that fundamental constant itself. When we use terms like “one light-year” or “one light-second,” we’re talking about distances in terms of time: the amount of distance that light travels in one year (or one second), for example. If we want to convert “time” into a distance, we need to multiply it by the speed of light in a vacuum.
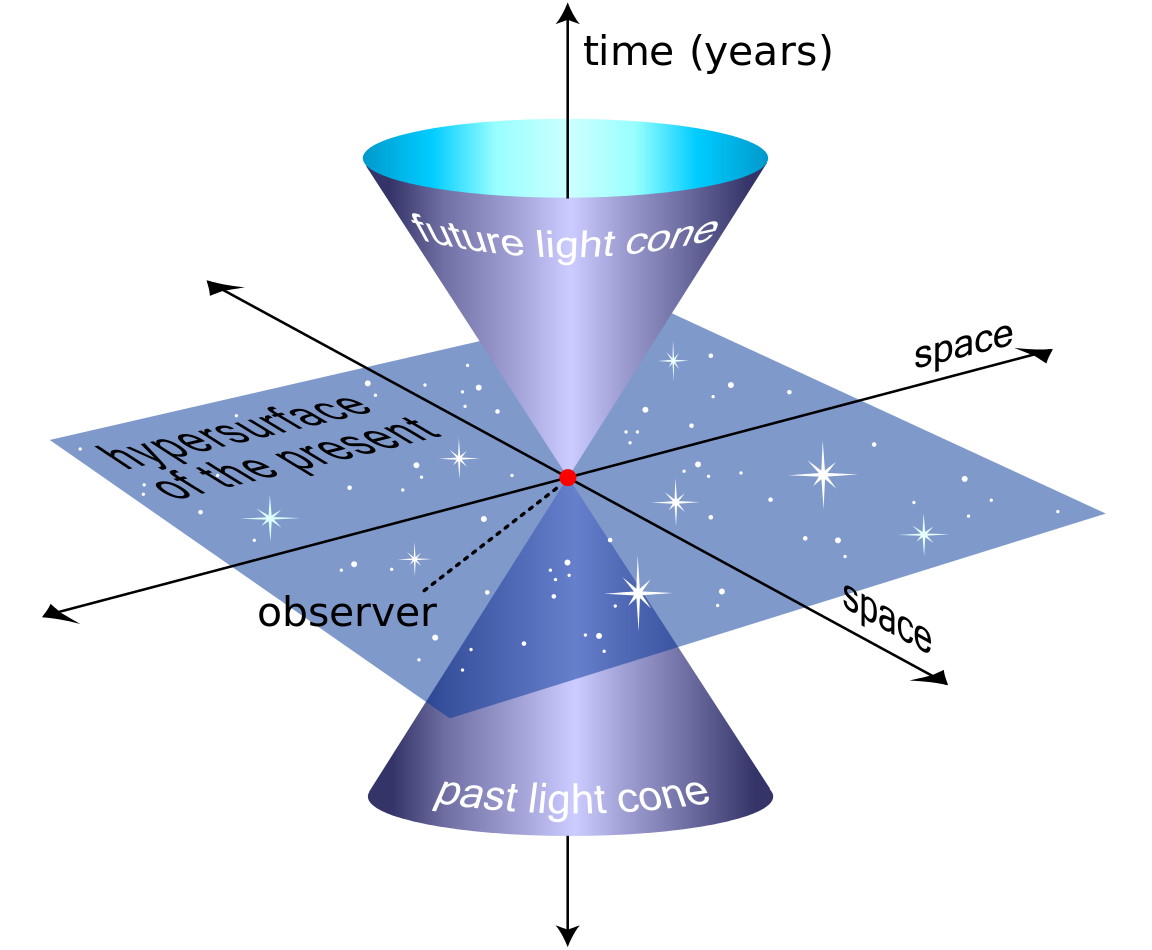
But the second way requires an enormous leap to understand: something that eluded the greatest minds of the late 19th and early 20th centuries. The key idea is that we’re all moving through the Universe, through both space and time, simultaneously. If we’re simply sitting here, stationary, and not moving through space at all, then we move through time at a very specific rate at which we’re all familiar: one second per second.
However — and this is the key point — the faster you move through space, the slower you move through time. The other dimensions are not like this at all: your motion through the x dimension in space, for example, is completely independent of your motion through the y and z dimensions. But your total motion through space, and this is relative to any other observer, determines your motion through time. The more you move through one (space or time), the less you move through the other.
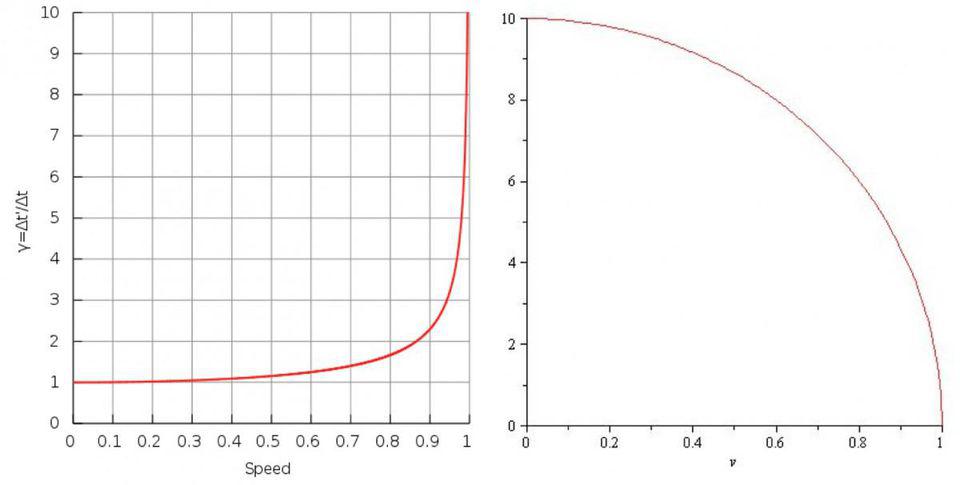
This is why Einstein’s relativity gives us concepts like time dilation and length contraction. If you move at very low speeds compared to the speed of light, you won’t notice these effects: time appears to move at one second per second for everyone, and lengths appear to be the same distance for everyone at speeds normally achievable on Earth.
But as you approach the speed of light — or rather, as you perceive an object where the relative speed between you and it is close to the speed of light — you’ll observe that it’s contracted along its direction of relative motion, and that clocks appear to run at a slower (dilated) rate relative to your own clocks.
The reason underlying this, as realized by Einstein, was straightforward: it’s because the speed of light is the same for all observers. If you imagine that a clock is defined by light bouncing back and forth between two mirrors, then watching someone else’s clock as they move close to the speed of light will inevitably result in their clock running slower than your own.
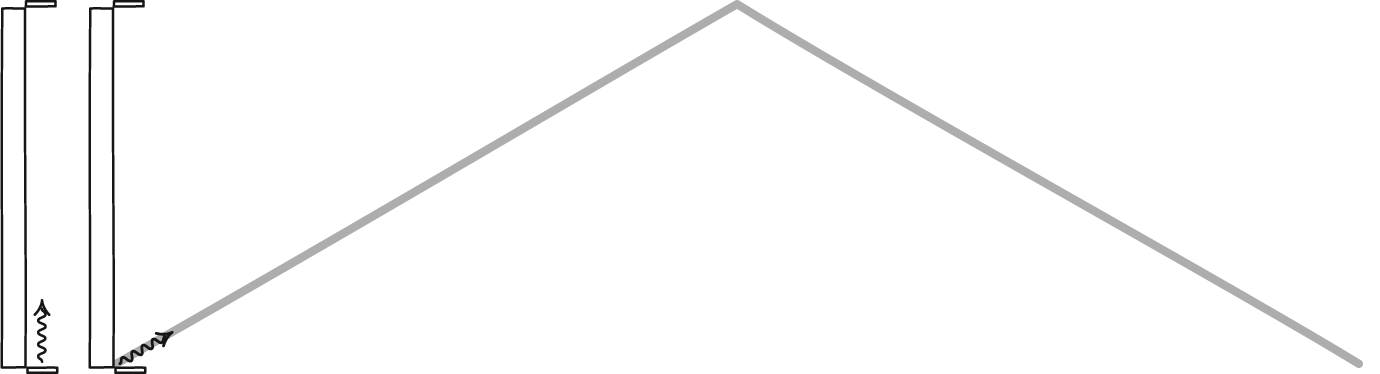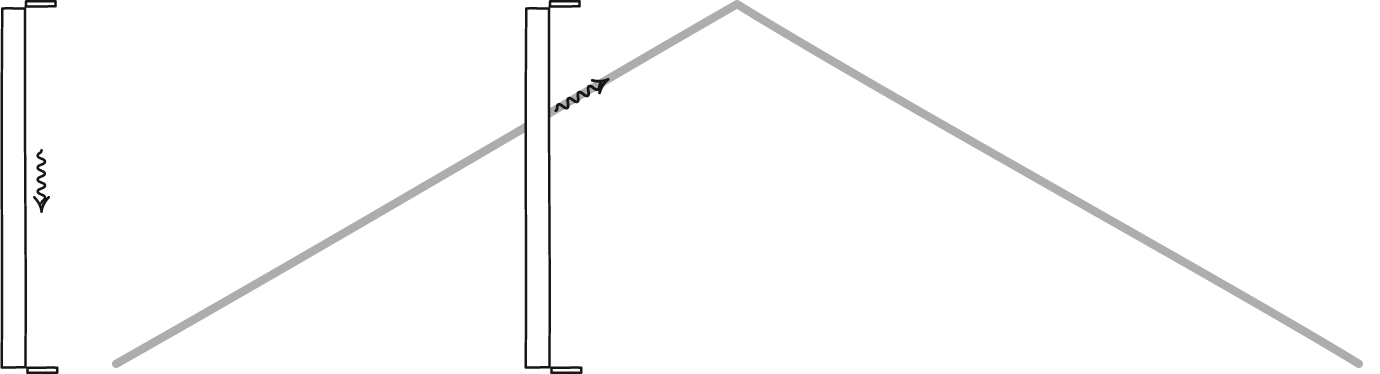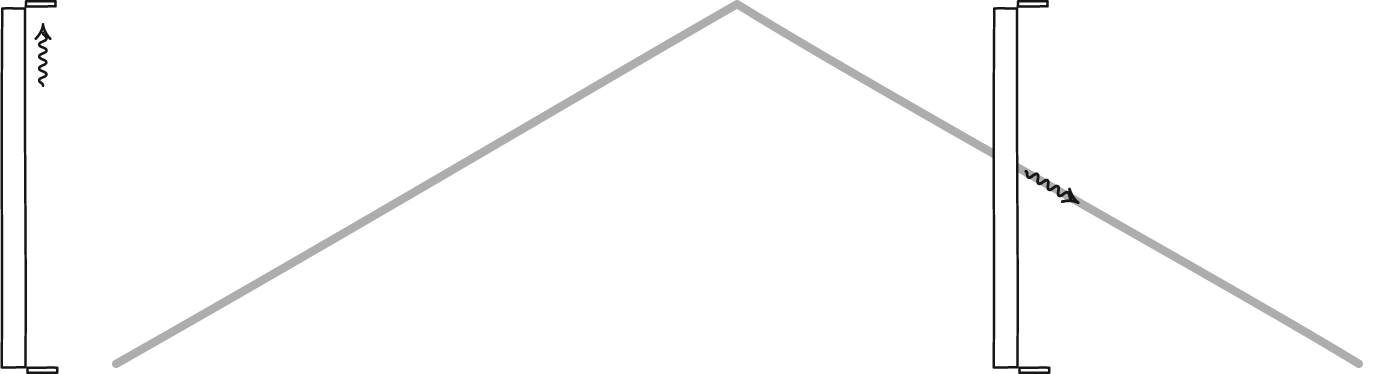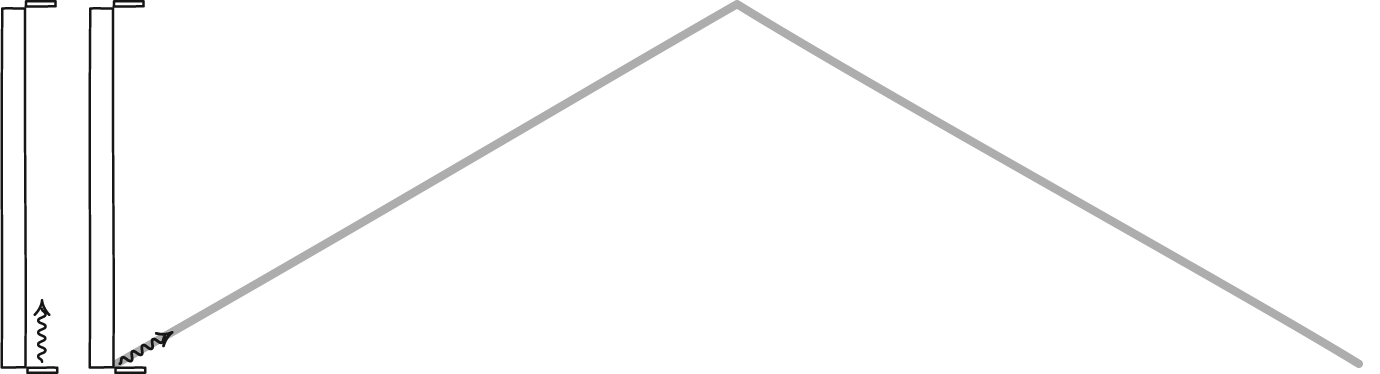
But there’s an even deeper insight here, which initially eluded even Einstein himself. If you treat time as a dimension, multiply it by the speed of light, and — here’s the big leap — treat it as though it were imaginary, rather than real, then we can define a “spacetime interval” the same way we defined distance earlier. Only, since the imaginary number i is just √(-1), this means that the spacetime interval is actually d = √(x² + y² + z² – c²t²). [Note the minus sign attached to the time coordinate!]
In other words, the transformation from “motion through or separation in space” to “motion through or separation in time” is also a rotation, but it’s a rotation not in the cartesian coordinates of space (where x, y, and z are all real numbers), but through the hyperbolic coordinates of spacetime, where if the space coordinates are real, then the time coordinate must be imaginary.
In a great twist of fate, the person who first put these puzzle pieces together was Einstein’s former teacher, Hermann Minkowski, who noted in 1907/8 that,
“Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”
With Minkowski’s mathematical rigor behind it, the concept of spacetime was not only born, but was here to stay.
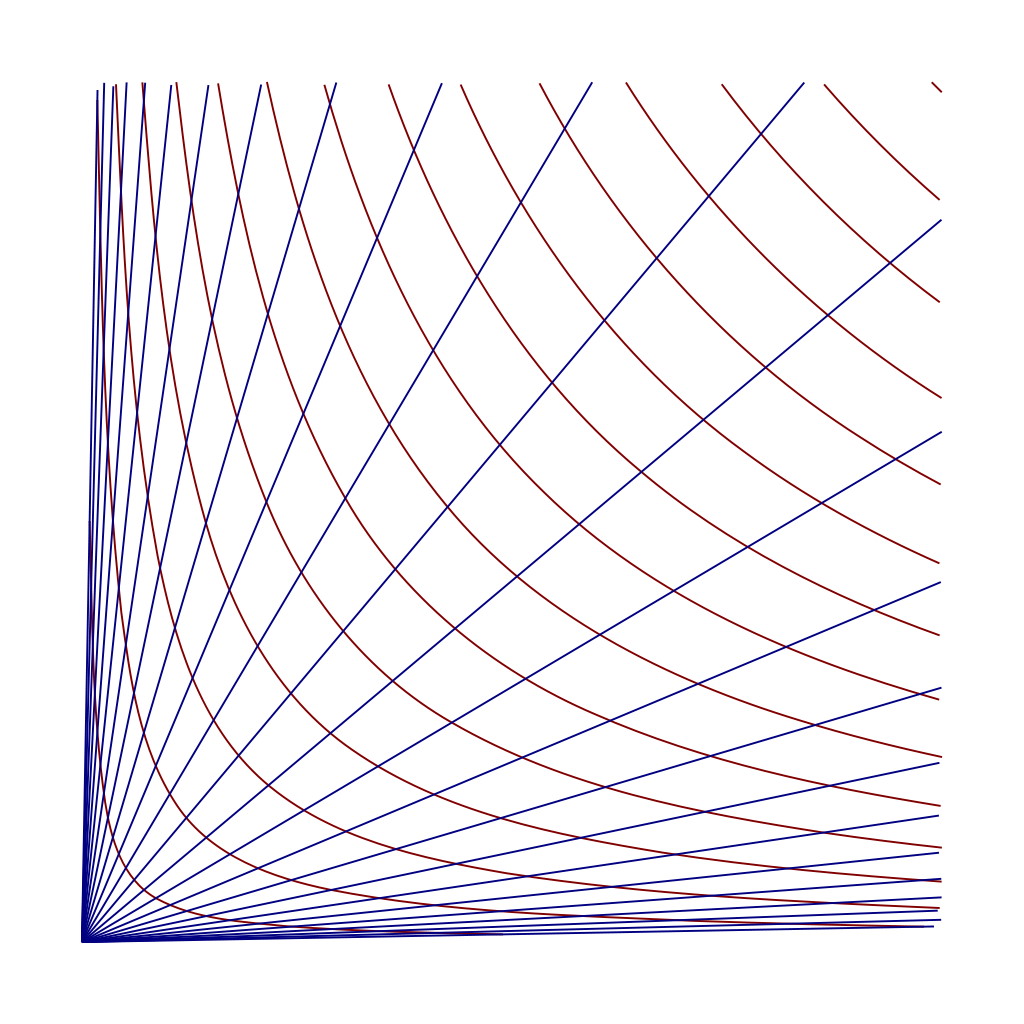
What’s remarkable about all of this is that Einstein, despite lacking the mathematical insight to understand exactly how the dimension of time was related to the three conventional dimensions of space, was still able to piece together this key physical insight. Increasing your motion through space decreased your motion through time, and increasing your motion through time decreased your motion through space. All measurements of space and time are only meaningful relative to the observer in question, and depend on the relative motion of the observer to the observed.
And yet, the spacetime interval remains invariant. No matter who is doing the observing or how quickly they’re moving, the combined motion of any object through spacetime is something all observers can agree on. In some ways, the success of relativity was made all the more impressive in light of Minkowski’s assessment of Einstein. Speaking to his (later) student, Max Born, Minkowski had the following to say,
“For me [relativity] came as a tremendous surprise, for in his student days Einstein had been a real lazybones. He never bothered about mathematics at all.”
Fortunately, in physics, the Universe itself — not anyone’s opinion — is the ultimate arbiter of scientific truth.