Ask Ethan: How do magnetic fields split energy levels?

One of the most remarkable things about physics is how universal it is. If you take the same species of atomic nucleus — with a fixed number of protons and neutrons — then there will only be a fixed set of energy levels that the electrons orbiting that nucleus can occupy. As the electrons transition between the various energy levels, they emit (as they fall to lower energy levels) and absorb (as they rise to higher energy levels) photons of a very specific wavelength and energy: only those wavelengths and energies allowable by the rules of quantum mechanics. The values for these energy levels are universal: the same for all atoms of the same species everywhere and at all times throughout the Universe.

Until, that is, you apply either an external electric or magnetic field. All of a sudden, these energy levels split, and take on a great variety of values, with the amount of splitting depending entirely on the strength of the field applied. But how is this possible? That’s what Jon Coal wants to know, asking:

“Hey, have you ever done a piece on the Zeemen effect? […] I guess the thing I’m trying to put my head around is that theoretically light can’t be bent by a magnetic or an electric field. So these effects, Zeeman and Stark, are they modifying the atomic structure [itself]?”

The Zeeman effect is what we see when we apply an external magnetic field, and the Stark effect is what we see when we apply an external electric field. Both of them really do split the atomic energy levels, but not in the way you might expect.

Although we normally conceive of atoms as nuclei with electrons orbiting them, if the environment in which an atom is placed has a magnetic or electric field within it, the orbital properties of the electrons, including the energy levels that they occupy, will change. As a result, the photons they emit or absorb will be of different wavelengths than if the field were removed.

First off, it’s true: light, despite being an electromagnetic wave itself, cannot be bent by either a magnetic or an electric field. Electric and magnetic fields do, quite famously, cause particles-in-motion to bend, but only if those particles themselves are composed of non-zero electric charges.

• A proton can be bent by either: a proton that’s either stationary or in motion will be accelerated in the direction of an external electric field and a proton in motion will be accelerated in a direction that’s perpendicular to both its motion and the direction of the applied magnetic field.
• An electron can be bent by either: an electron that’s either stationary or in motion will be accelerated opposite to the direction of an external electric field and an electron in motion will be accelerated in a direction that’s mutually perpendicular to both its motion and the direction of the applied magnetic field.
• A neutron cannot be bent by an electric field, because it’s electrically neutral, but will still respond to an applied magnetic field because it’s inherently made up of quarks: charged particles that move around inside of it. The neutron has an intrinsic magnetic moment to it that’s almost twice as strong as the electron’s, and will be affected by an external magnetic field.

But a photon is uncharged and isn’t made up of any charged constituents. While external magnetic and electric fields can polarize that light, changing the direction of its fields while it propagates, they cannot bend the light itself.

Light is nothing more than an electromagnetic wave, with in-phase oscillating electric and magnetic fields perpendicular to the direction of light’s propagation. The shorter the wavelength, the more energetic the photon, but the more susceptible it is to changes in the speed of light through a medium.

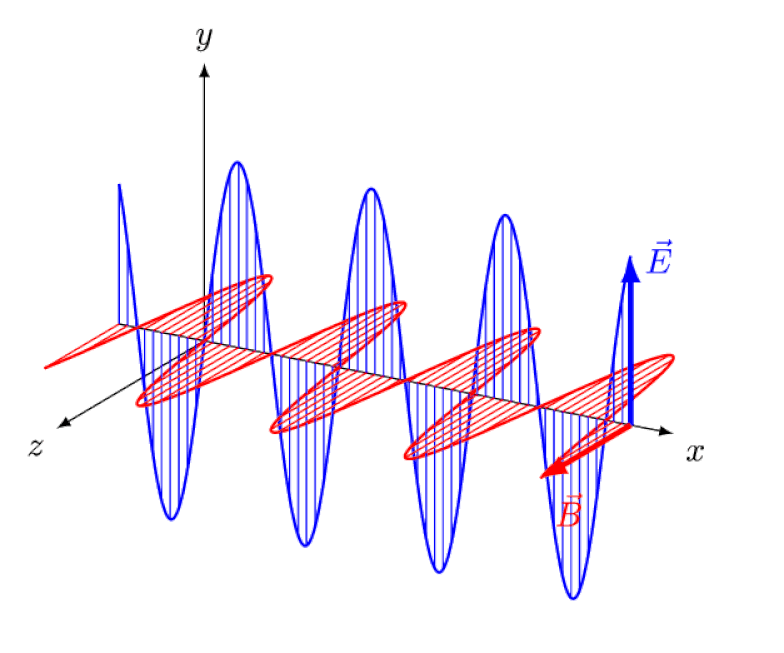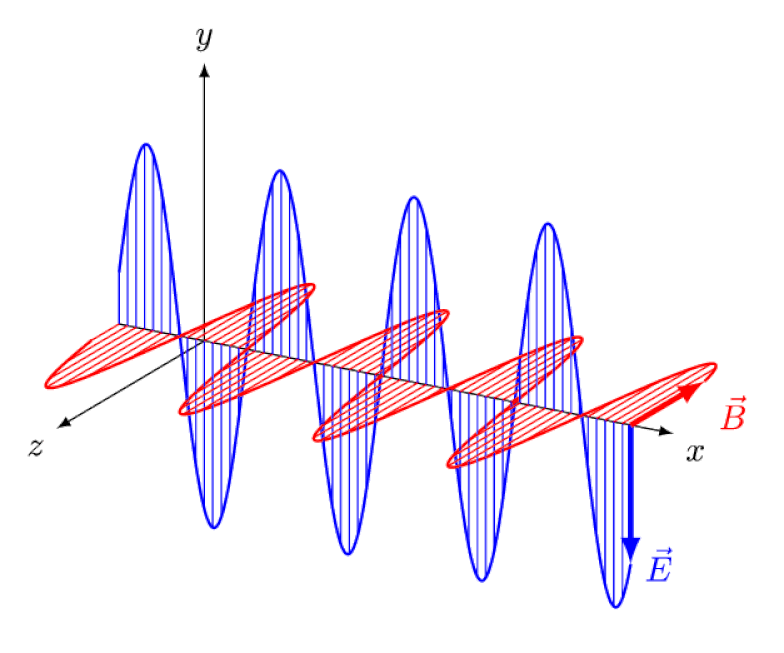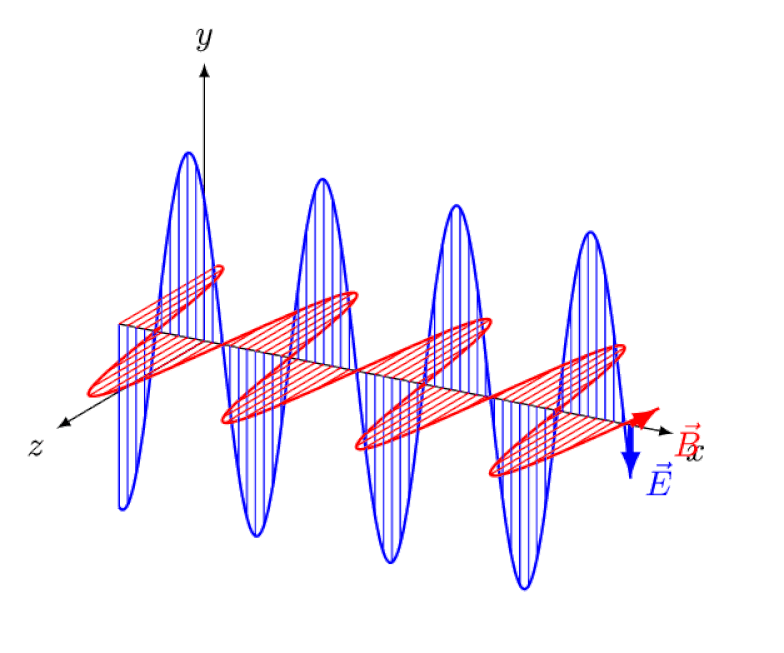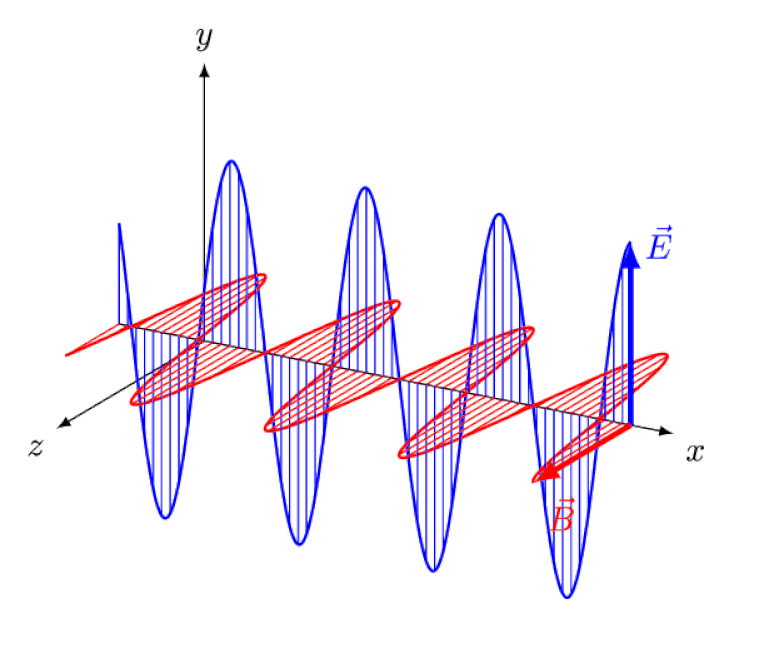
But the Zeeman effect and the Stark effect are not only both real, they were both experimentally observed long ago. The challenge for theorists is not to demonstrate which effects cannot be at play — which the fact that photons can’t be deflected by electric or magnetic fields shows — but rather to uncover the critical cause of the observed effect, complete with explaining its magnitude and the conditions under which it appears.

The confusion arises here because it isn’t because atoms emit light and then that light propagates through a region where there’s an electric or magnetic field; that’s one way to get polarization, but not a way to get the splitting of energy levels, as in the Zeeman effect or the Stark effect.

Instead, the way you split the energy levels within an atom (or a molecule, if you prefer more complex chemistry) is by applying the electric or magnetic field to the atom (or molecule) itself, before the critical transition from one energy level to another occurs. Those photons are created within an atom or molecule that already had this external field applied to them, and that’s where this splitting occurs. We should’ve expected it, because there’s a subtle way to catch the same underlying effect occurring in nature even without an external field: through the fine structure of atoms.

Electron transitions in the hydrogen atom, along with the wavelengths of the resultant photons, showcase the effect of binding energy and the relationship between the electron and the proton in quantum physics. The Bohr model of the atom provides the coarse (or rough, or gross) structure of the energy levels, but this already was insufficient to describe the fine and hyperfine structure, which had been seen decades prior.

Most of us, when we think about the energy levels in atoms, go all the way back to the Bohr model, which itself was revolutionary. In 1912, Bohr postulated that the electrons don’t quite orbit around an atom’s nucleus the way planets orbit the Sun: held in place through an invisible, central force. Instead, Bohr’s idea stated, there were only certain particular states that electrons were allowed to orbit in: orbitals, as opposed to possessing any combination of speed and radius leading to a stable orbit in the case of planetary motion.

Bohr recognized that the electron and nucleus were both very small, had opposite charges, and knew that the nucleus had practically all of the mass. His groundbreaking contribution was understanding that electrons can only occupy certain energy levels, which is where the term “atomic orbitals” first came from.

Electrons can orbit the nucleus only with particular properties, leading to the absorption and emission lines characteristic to each individual atom: the Bohr atom. But even though this is how we typically picture atoms today, back in 1912, when Bohr first proposed it, we knew it couldn’t be the full story.

A variety of energy levels and selection rules for electron transitions in an iron atom. There are only a specific set of wavelengths that can be emitted or absorbed for any atom, molecule, or crystalline lattice. Although each atom has a unique spectrum of energies, all atoms share certain quantum properties.

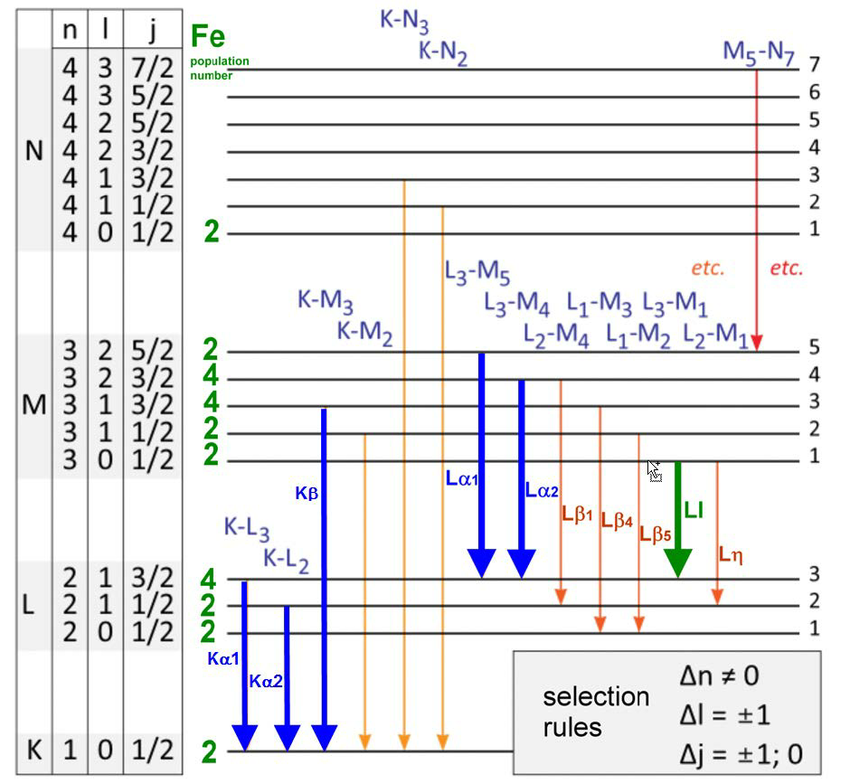
In 1887, when Michelson and Morely were constructing and performing their famed experiment that would disprove the need for an aether, or an at-rest medium in some particular frame of reference for light to travel through, they were studying very closely the emission and absorption properties of the hydrogen atom. Lo and behold, these results, already 25 years old by the time the Bohr atom was first proposed, already stood in conflict with the Bohr model’s predictions.

The Bohr model, for instance, predicted that the 2nd energy level of hydrogen the first excited state that would have both

• s-orbitals (capable of holding 2 electrons)
• and p-orbitals (capable of holding 6 electrons)

would yield the same energies for all 8 possible electron configurations. But Michelson and Morely’s results demonstrated both small shifts away from the Bohr value and also multiple additional states. Although the departure from the Bohr model was slight, it was significant, with the most stunning difference being that some energy levels appeared to split into two, whereas Bohr’s model only possessed one energy state they could occupy.

In the Bohr model of the hydrogen atom, only the orbiting angular momentum of the point-like electron contributes to the energy levels. Adding in relativistic effects and spin effects not only causes a shift in these energy levels, but causes degenerate levels to split into multiple states, revealing the fine structure of matter atop the coarse structure predicted by Bohr.

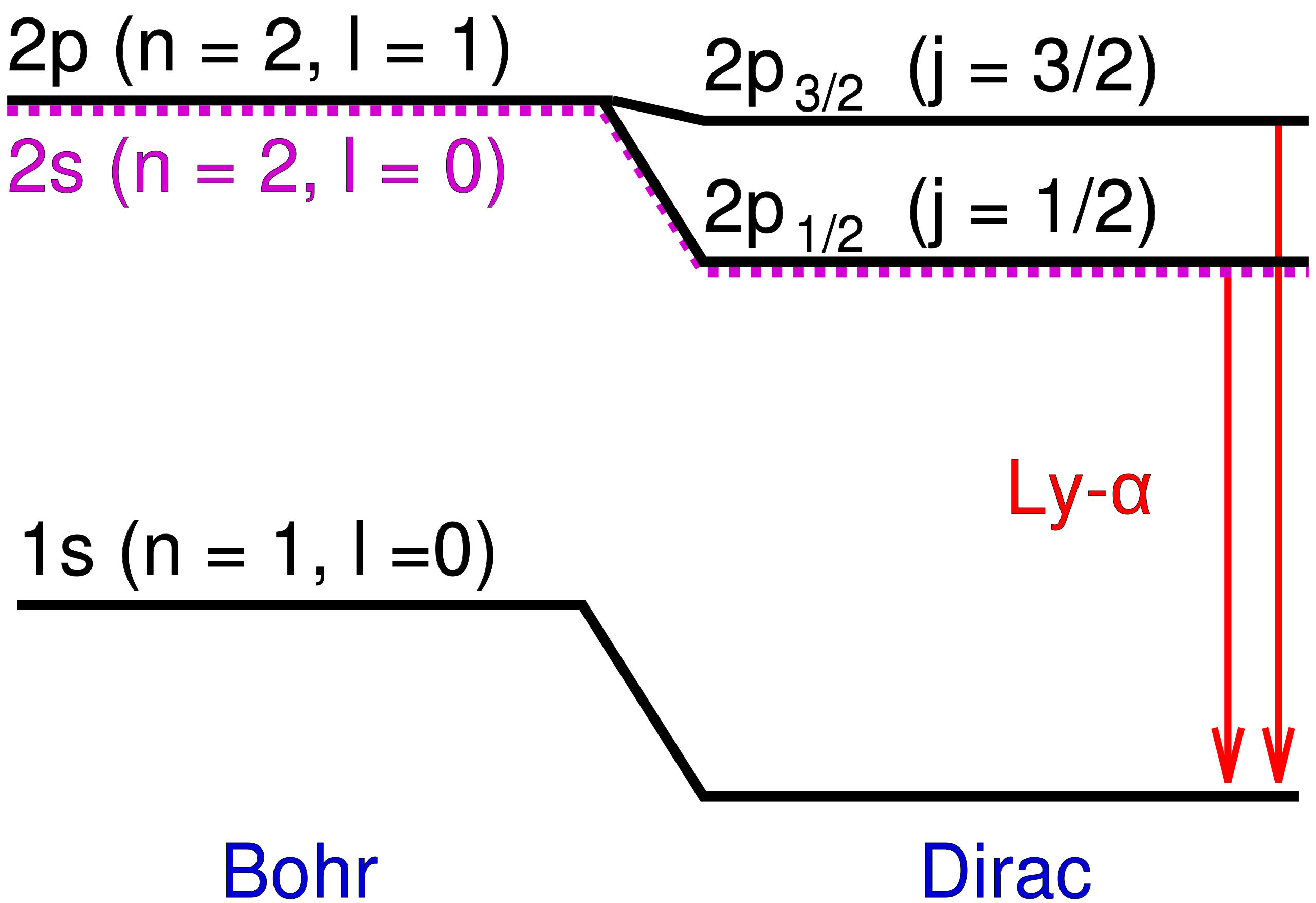
Those additional energy levels were extremely close to one another, and were also very close to Bohr’s predictions. But the differences were real, and so the task for physicists was to explain what caused them?

The key to the answer lay in the assumptions that Bohr used in creating his model: that electrons were charged, spinless particles that orbited the atomic nucleus at speeds significantly lower than the speed of light. This was good enough to explain the coarse structure of atoms, or the general nature of energy levels, but not this additional, more subtle structure.

It only took 4 years for the first theoretical attempt at explaining this to come about, by way of physicist Arnold Sommerfeld. Sommerfeld’s big realization was this: if you modeled a hydrogen atom using Bohr’s simplistic model, but took the ratio of a ground-state electron’s speed and compared it with the speed of light, you’d get a certain value. Sommerfeld called that value α, which we know today as the fine-structure constant. Once you folded it into Bohr’s equations, you indeed found that it caused a shift in the energy levels observed, accounting for not just an atom’s coarse structure in terms of energy levels, but this more precise “fine structure,” as it’s still called today.

In the absence of a magnetic field, the energy levels of various states within an atomic orbital are identical (L). If a magnetic field is applied, however (R), the states split according to the Zeeman effect. Here we see the Zeeman splitting of a P-S doublet transition. Other types of splitting occur owing to spin-orbit interactions, relativistic effects, and interactions with the nuclear spin, leading to the fine and hyperfine structure of matter.

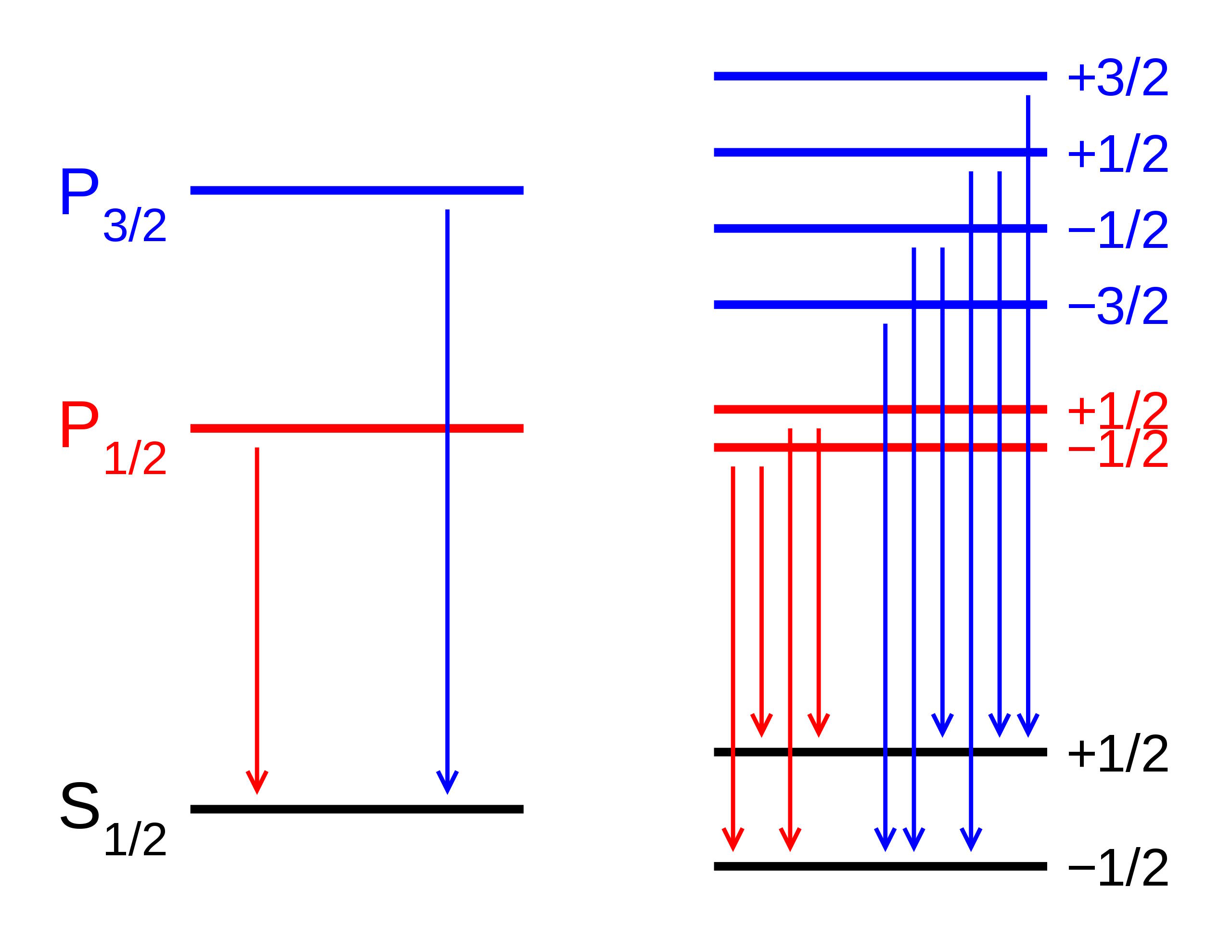
But if you look more intricately into the structure of atoms, you’ll discover that even with Sommerfeld’s accounting for the effect of the motion of electrons, that doesn’t quite explain everything there is. That’s because Sommerfeld only explained the first of three major effects that serve as fine structure corrections to Bohr’s coarse model.

1. Electrons and other quantum particles can have speeds that move close to the speed of light.
2. Electrons don’t merely have angular momentum from their orbits around the atomic nucleus, but an intrinsic amount of angular momentum known as spin, with a value of ±ħ/2,
3. and electrons also exhibit an inherent set of quantum fluctuations to their motion known as zitterbewegung.

The second one is of particular relevance, as the electron’s spin, whether +ħ/2 or –ħ/2 (positive or negative relative to the electron’s orbital angular momentum), will produce a magnetic moment, and that magnetic moment will interact, either positively or negatively, with the electron’s orbital angular momentum.

But we can go even deeper than this. There’s an even more subtle effect than fine structure that arises in atoms and molecules: hyperfine structure.

The atomic transition from the 6S orbital in a cesium-133 atom, Delta_f1, is the transition that defines the meter, second and the speed of light. Slight changes in the observed frequency of this light will occur based on motion and the properties of spatial curvature between any two locations. Spin-orbit interactions, as well as various quantum rules and the application of an external magnetic field, can cause additional splitting at narrow intervals in these energy levels: examples of fine and hyperfine structure.

If electrons, charged particles, have an intrinsic spin and an intrinsic magnetic moment, then that can interact with anything that makes a magnetic field, including:

• the charged, spinning atomic nucleus,
• any asymmetries within the electric field of the atom itself,
• and, if these electrons are in a molecule instead of a monatomic atom, the interaction between the magnetic moments of the different atomic nuclei and the magnetic field generated by the molecule’s overall rotation.

Any electromagnetic interaction between charged or magnetized particles can alter the energy levels inside atoms and/or molecules, with Bohr’s original model providing the coarse, general structure, with particle motions, fluctuations in those motions, and the spin-orbit interaction providing fine-structure corrections to that coarse structure, and then with more subtle interactions between electrons and additional internal and external electromagnetic effects providing hyperfine structure atop the coarse and fine structure.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

All of that is needed to explain the structure of the energy levels within atoms and molecules, and that’s all before we even begin to consider externally applied electric and magnetic fields.

This graph shows the Zeeman splitting in the 5s orbitals of a Rubidium-87 atom. Note that as the field strength increases, the amount of splitting increases as well, dependent on properties such as the quantum spin states of the various electrons. The Zeeman effect is generally much smaller than the Stark effect.

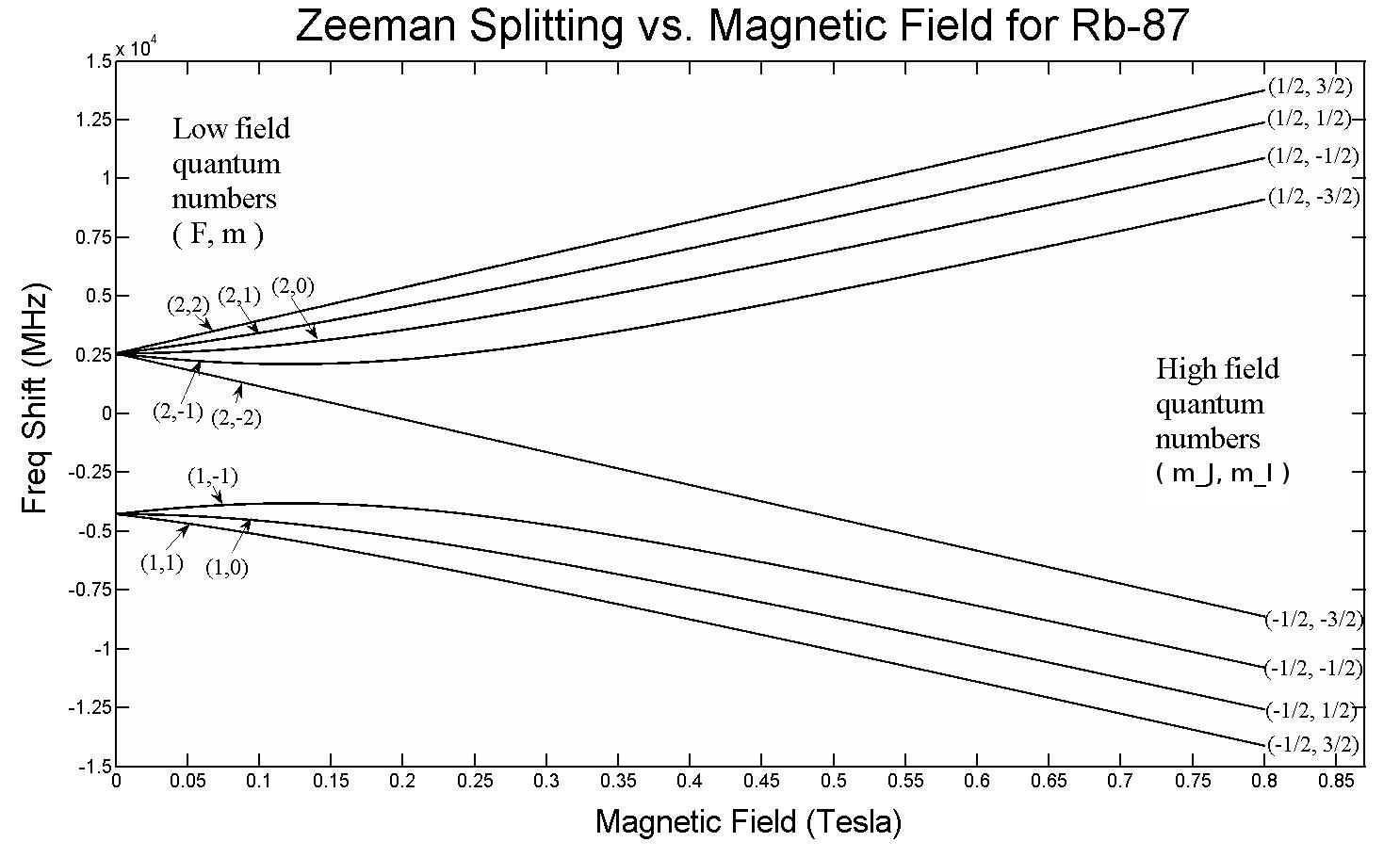
But just from this setup, we’ve already almost arrived at the solution! If you apply an external electric or magnetic field to any atom or molecule, then these energy levels are going to be affected as well by the same mechanism: through the interaction of these spinning, orbiting, charged and intrinsically magnetic electrons with those fields. Only, there’s a major difference this time: whereas the hyperfine structure within atoms and molecules always has a small effect compared to the fine structure effects, and the fine structure effects are small compared to the coarse structure of atoms, the magnitude of the applied electric and magnetic fields can take on any value at all, only limited by our laboratory setups.

This means that if you apply an external electric field, it will interact with all the different components of your atoms and molecules, causing the electron energy levels within the atoms to split further. Similarly, if you apply an external magnetic field, it will have the same effects: splitting the electron energy levels even further than before. While, in most cases, these effects will simply “grow” the splittings already induced by the fine and hyperfine structure within atoms, in some cases, it can even cause additional, new splits in the energy levels: splits that go away entirely if the external field is turned off.

The Stark effect, which splits the energy levels within atoms when an external electric field is applied, can be so strong that it can overcome not only the fine and hyperfine structure splitting within atoms and molecules, but the coarse Bohr structure itself.

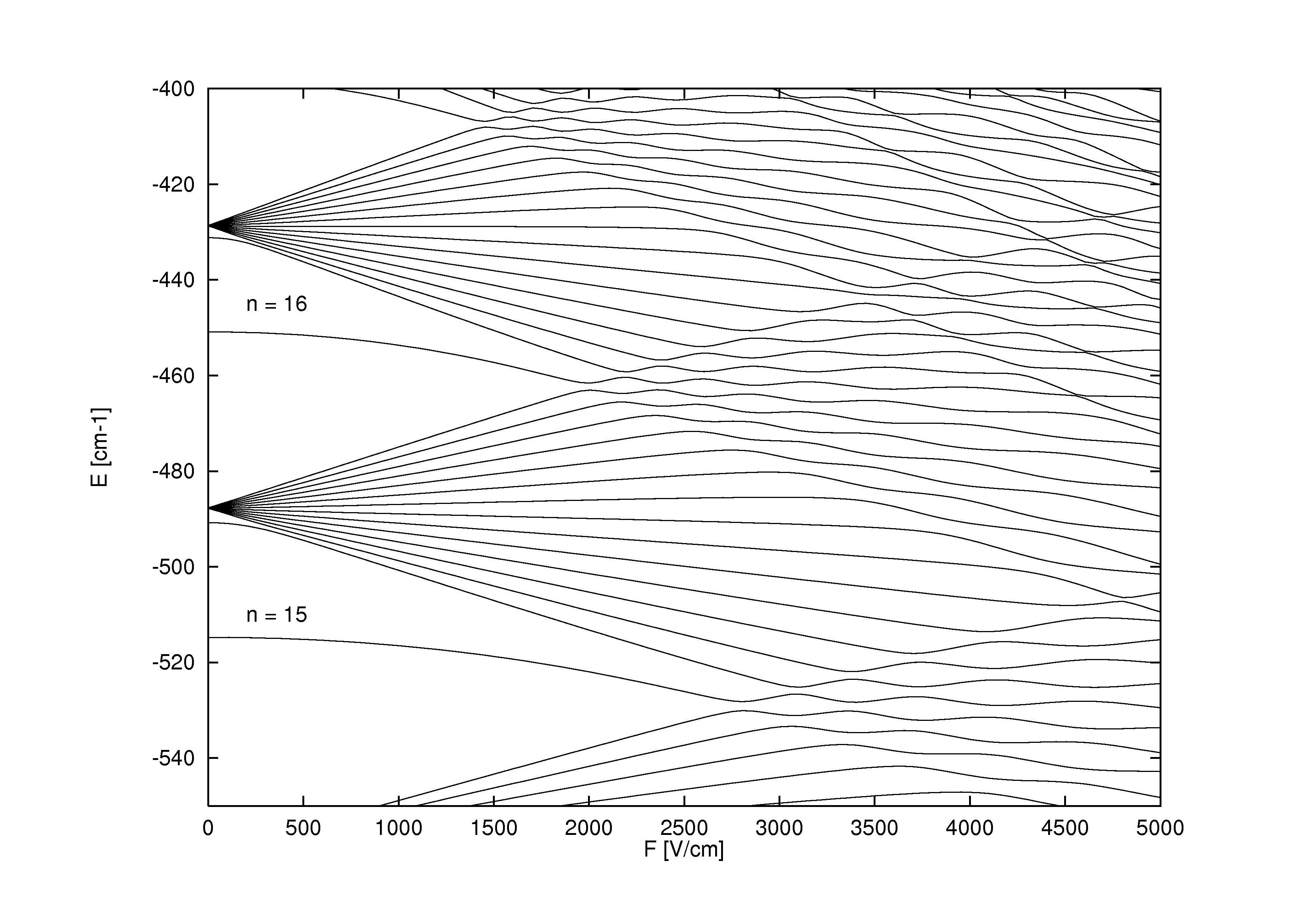
What’s extra cool about the Zeeman effect and the Stark effect is that both are old: older than most of the story about fine and hyperfine structure in atoms. Pieter Zeeman discovered the effect of the magnetic splitting of spectral lines way back in 1896, while Johannes Stark discovered the analogous electric splitting effect for emission and absorption lines way back in 1913. Before we even recognized that electrons had spin, that a spin-orbit interaction was occurring, or that energy levels could be affected by magnetic and electric components within atoms and molecules themselves, we had experimentally discovered these effects.

It’s often the case, in physics and in many other sciences, that experimental or observational “discoveries” far precede the theoretical explanation we later wind up uncovering for them. In both the cases of the Zeeman and Stark effects, these were vitally important discoveries on the road to the modern development of quantum mechanics, and they were justly awarded Nobel Prizes, respectively, in 1902 and 1919. Generally, the Stark effect can be enormous, and so spectral line splitting, if you’re looking to “tune” an atom to absorb or emit at a particular wavelength, is controlled with magnetic, rather than electric, fields. Nevertheless, the key to creating it is to apply your field to the emitting or absorbing atom, not the photon once it’s already in flight!

Send in your Ask Ethan questions to startswithabang at gmail dot com!