Ask Ethan #36: The Amazing Spinning Electron
Even adding just one extra particle makes all the difference.
“Art has a way of confronting us, of reminding us, of engaging us, in what it means to be human, and what it means to be human is to be flawed, is to be contradictory, is to be often weak, and yet despite all of these what we would consider drawbacks, that we’re also quite beautiful. Spin is the opposite.” –Junot Diaz
It’s the end of the week here on Starts With A Bang, and that means it’s time again for another Ask Ethan column. You’ve been sending in your questions and suggestions all week, and — as promised — I’ve chosen my favorite to share with you and answer for all the world. This week’s question comes from Bill Galloway, who asks:
As I was reading your answer on Lasers it reminded me of a question I have had for a long time about the Pauli exclusion principle. I am not a physicist so my apologies if I am not asking the question correctly. My understanding is that the two electrons in a hydrogen molecule have to have opposite spin. So, does the spin of the electrons change as they form a molecule or is it only possible for hydrogen atoms with opposite spins to form a molecule?
There’s a lot encapsulated in Bill’s question, so let’s start with the Pauli Exclusion Principle.
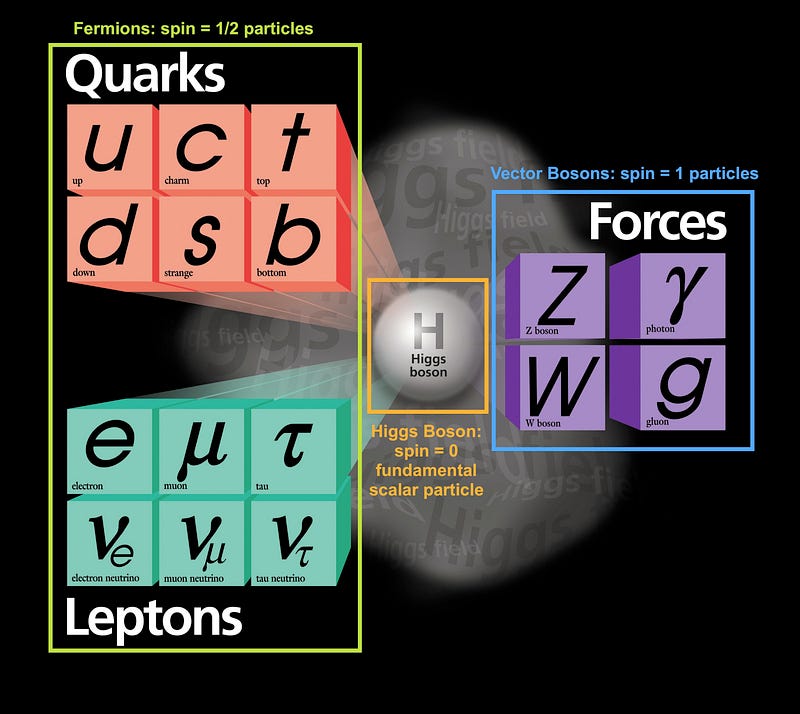
Despite the huge diversity of the different types of fundamental particles that exist in the Universe — as evidenced by the Standard Model, above — they can all be divided into two types:
- Fermions, or particles with half-integer spin: ±1/2, ±3/2, ±5/2, etc.
- Bosons, or particles with integer spin: 0, ±1, ±2, etc.
What’s kind of amazing is that composite particles behave as either Fermions or Bosons as well, with your familiar friends the proton and neutron behaving as fermions with spins of ±1/2, just like electrons. Each particle has a certain set of quantum states it can occupy with discrete energy levels, angular momentum values, spin directions, etc.
And the major difference between fermions and bosons is that if you have two identical particles, you can put as many bosons as you like into the same quantum state, but identical fermions are excluded from occupying the exact same state.
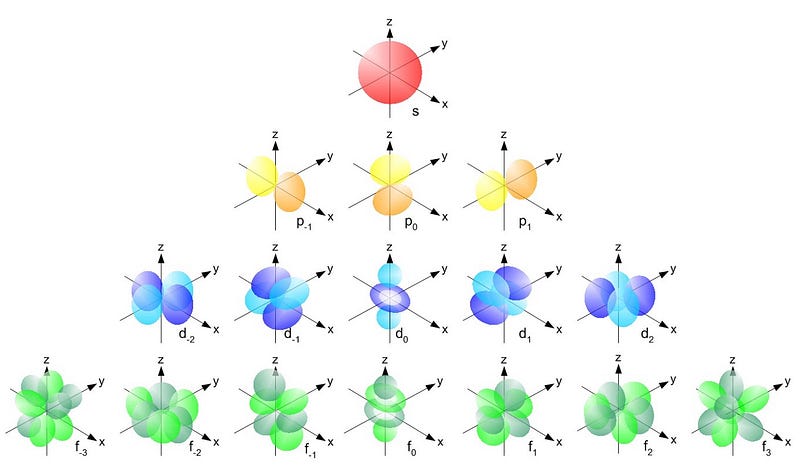
If the electron weren’t a fermion (and were a boson instead), then whenever you had an atom, you could pack as many electrons as you wanted into the lowest energy state (in red, above) as you wanted! But the electron is a fermion, and so is subject to the Pauli exclusion rule. The lowest energy state can accept two electrons, because one can be spin +1/2 and the other can be spin -1/2, but if you add a third electron, you need to hop up into a different quantum state.
And the way quantum states work in atoms is that you can move up to a higher energy state (denoted by n, below), and then to progressively higher angular momentum states (l, below).
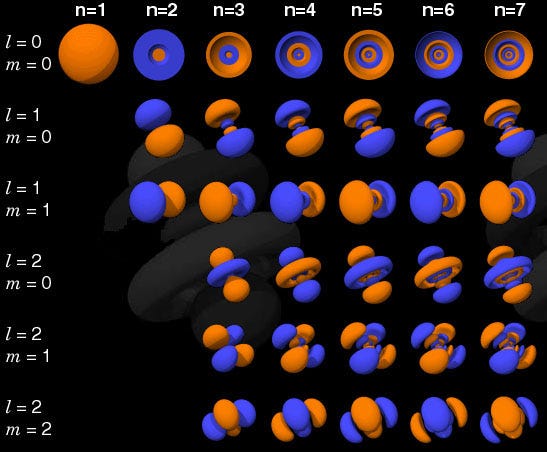
So the l = 0 states are the s-orbitals, the l = 1 states are the p-orbitals, the l = 2 states are the d-orbitals, and so on. This is why the periodic table of the elements has the structure that it’s observed to have: with 2 elements in the top row (filling n=1, l=0, m=0, and spin = ±1/2), 8 elements in the second row (n=2, l=0, m=0, and spin = ±1/2, and n=2, l=1, m=1,0, or -1 and spin = ±1/2), 18 elements in the third row (n=3, l=0, m=0, and spin = ±1/2; n=3, l=1, m=1,0, or -1 and spin = ±1/2; and n=3, l=2, m=2,1,0,-1 or -2 and spin = ±1/2), etc.
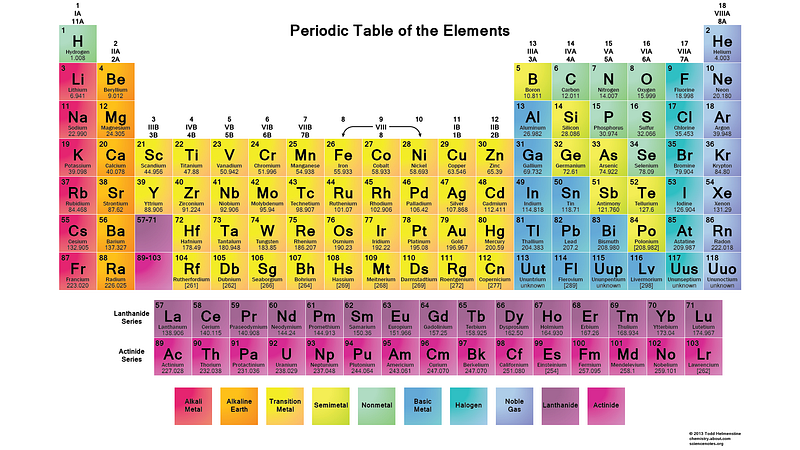
So when you see the periodic table get an extra 6, 10, 14, etc., entries with every new row, the Pauli exclusion principle is the reason why!
Even though we have no way of distinguishing one electron from another (because they’re identical), each atomic system is unique. In other words, if I have four different hydrogen atoms in the ground state, they’re not going to be required to occupy different energy states.
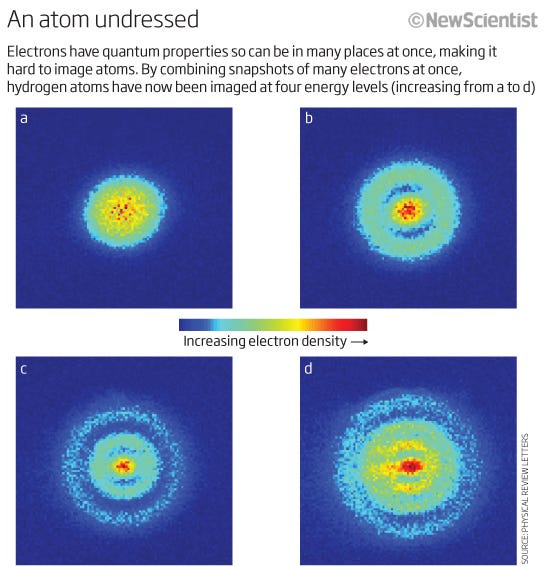
In fact, because the atomic nuclei (the protons) are distinct from one another (i.e., not in the same nucleus, or in an overlapping quantum state in any sense), and the electrons are each bound to their own parent proton (i.e., not in overlapping quantum states with one another), a system of free hydrogen atoms would very likely have them be all in the ground state, for something that looks like this.

At least, that’s a reasonable way to set your system up initially. But if two of these hydrogen atoms come in contact with one another, they’re going to want to bond, and form a hydrogen molecule. After all, just like a hydrogen atom in the ground state is a little bit lighter — 13.6 eV lighter — than a free proton and a free electron due to binding energy, a hydrogen molecule is also a little bit lighter — by 4.52 eV — than two free hydrogen atoms.
But you’re right to worry about these electrons being in identical states. Because once these two separate atoms try to bond together, the electrons’ wavefunctions do try and overlap!
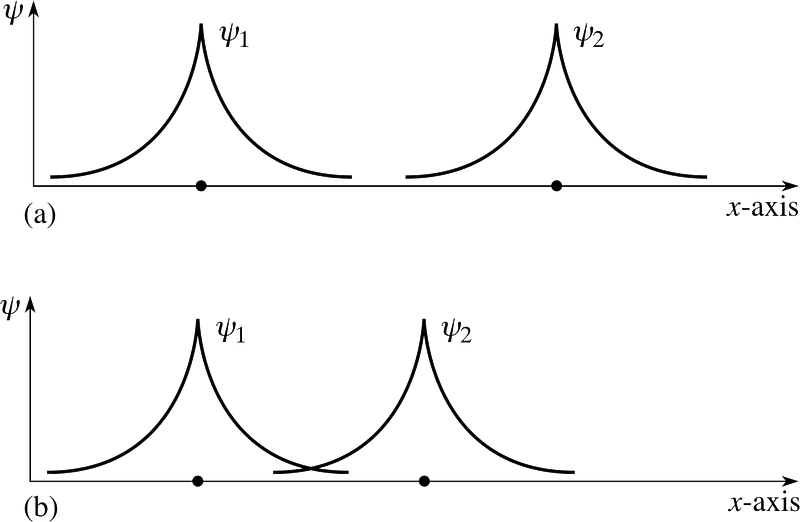
But remember that electrons are more than just particles with spin alone; they also have spatial wavefunctions, which is a fancy way to say they occupy space in a particular way. If I bring two hydrogen atoms close together, their spatial wavefunctions could be symmetric, like the diagram above shows, or they could be anti-symmetric, as shown in the diagram below.
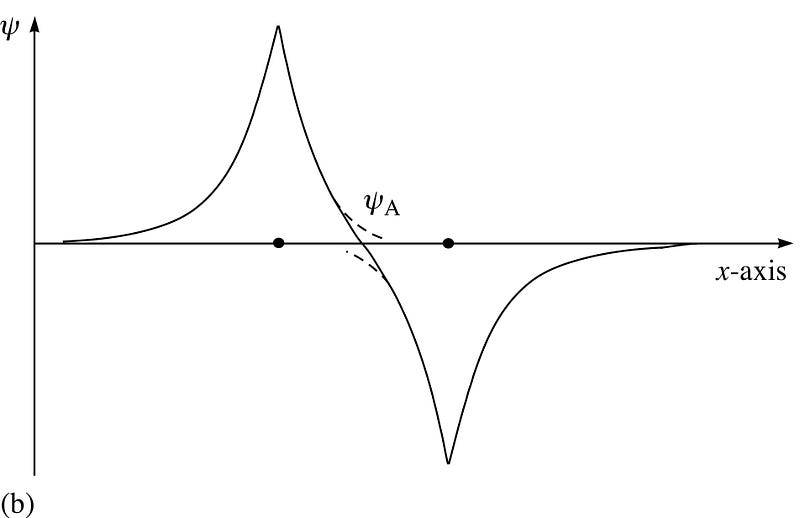
Now, here’s where the Pauli exclusion rule comes in, and it’s fascinating.
If the two hydrogen atoms come in with symmetric wavefunctions, then the spins of the electrons must be anti-aligned: if the first one was +1/2, the second must be -1/2, and if the first was -1/2, the second must be +1/2.
Similarly, if the two atoms came in with antisymmetric wavefunctions, then the spins of the electrons must be similarly-aligned: if the first is +1/2, the second must be +1/2, and if the first is -1/2, the second must be -1/2, too!
So if we ask how do two hydrogen atoms can be configured together, there are two possible configurations: either in a spatially-symmetric but spin-anti-aligned state, or in a spatially-anti-symmetric but spin-aligned state!
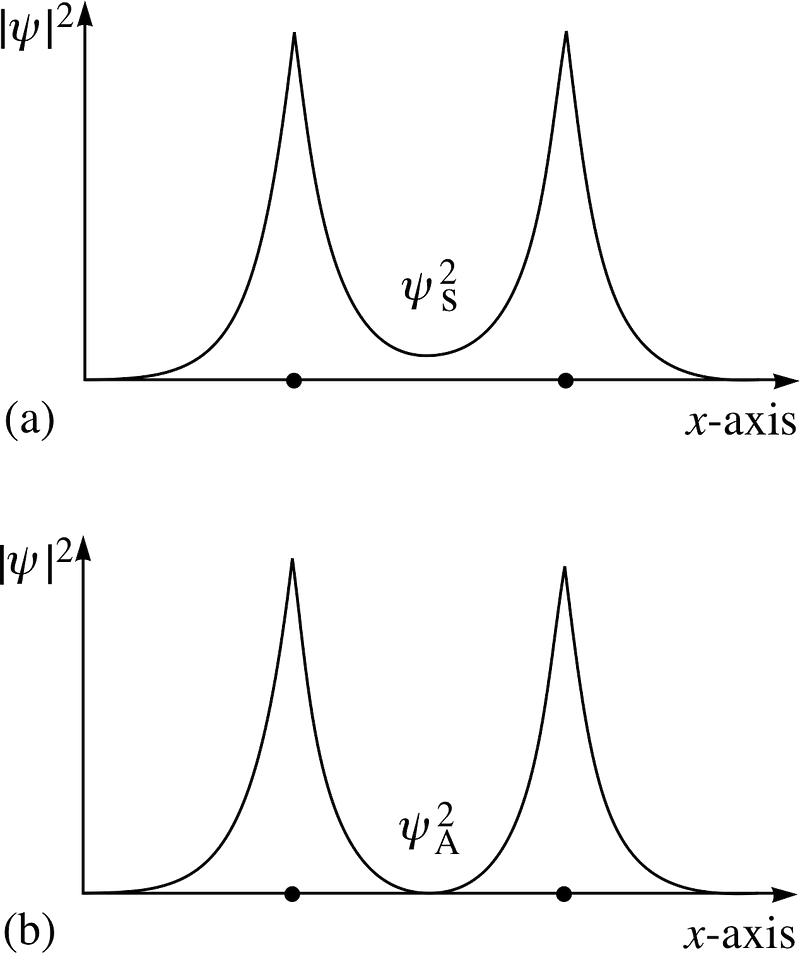
Look at these two combinations; for the top one, the wavefunctions overlap, indicating a bond, while for the lower one, the wavefunctions do not overlap, telling us this is an anti-bonding state!
We can actually compute — quantitatively, if we wanted — what the binding energy looks like for these two states.
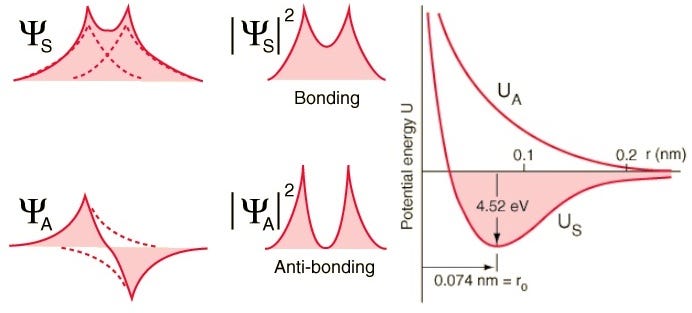
The anti-symmetric state, where the spins of the electrons are aligned with one another, do not bond; only the symmetric state, where the spatial wavefunctions are symmetric but the spins are anti-aligned, can form a bound hydrogen molecule!
So not only do you need two hydrogen atoms with symmetric spatial wavefunctions and opposite (+1/2 and -1/2) spins to form a hydrogen molecule, but you can clearly see how quantum mechanics forbids you from getting a third hydrogen in there ever, which is why you can have an H-atom, the H2-molecule, but you can never have H3 or higher!
And that’s how quantum mechanics allows you to form a hydrogen molecule, but only under very specific circumstances! Thanks for a great question, Bill, and if you want to see your question or suggestion answered on next week’s Ask Ethan, submit yours here for a chance!
Leave a comment on the Starts With A Bang forum at Scienceblogs!





