Why String Theory Is Both A Dream And A Nightmare

Few scientific ideas have been as polarizing as string theory. There are good reasons to both love it and hate it.

String theory is perhaps the most controversial big idea in all of science today. On the one hand, it’s a mathematically compelling framework that offers the potential to unify the Standard Model with General Relativity, providing a quantum description of gravity and providing deep insights into how we conceive of the entire Universe. On the other hand, its predictions are all over the map, untestable in practice, and require an enormous set of assumptions that are unsupported by an iota of scientific evidence.

For perhaps the last 35 years, string theory has been the dominant idea in theoretical particle physics, with more scientific papers arising from it than any other idea. And yet it has not produced even one testable prediction in all that time, leading many to decry that it hasn’t even risen to the standard of science. String theory is simultaneously one of the best ideas in the entire history of theoretical physics and one of our greatest disappointments. Here’s why.

When a meson, such as a charm-anticharm particle shown here, has its two constituent particles pulled apart by too great an amount, it becomes energetically favorable to rip a new (light) quark/antiquark pair out of the vacuum and create two mesons where there was one before. This is not a successful approach towards creating a free quark, but this realization did give rise to the string model of the strong interactions. (THE PARTICLE ADVENTURE / LBNL / PARTICLE DATA GROUP)

The story begins in the late 1960s, when particle accelerators were just entering their heyday. After the discovery of the antiproton in the 1950s, larger and more energetic particle accelerators began to be constructed, leading to an enormous suite of new particles that arose from colliding charged particles into other charged particle. The newly discovered particles came in three types:

baryons, like the proton, neutron, and their heavier cousins,
anti-baryons, like the anti-proton, anti-neutron, and heavier ones that matched 1-to-1 with the baryons,
and mesons, which came in a variety of masses and lifetimes, but which all were unstable and quickly decayed away.

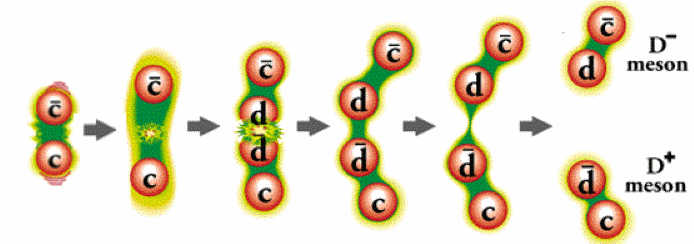
But one interesting thing to note was that mesons, before decaying, were like bar magnets. If you break a bar magnet (with a north and south pole), you don’t get an independent north and south pole, but rather two magnets each with their own north and south poles. Similarly, if you try to pull a meson apart, eventually it “snaps,” creating two separate mesons in the process.

Magnetic field lines, as illustrated by a bar magnet: a magnetic dipole, with a north and south pole bound together. These permanent magnets remain magnetized even after any external magnetic fields are taken away. If you ‘snap’ a bar magnet in two, it won’t create an isolated north and south pole, but rather two new magnets, each with their own north and south poles. Mesons ‘snap’ in a similar manner. (NEWTON HENRY BLACK, HARVEY N. DAVIS (1913) PRACTICAL PHYSICS)

This was initially where string theory began: as the string model of the strong nuclear interactions. If you envision a meson as a string, then pulling it apart increases the tension in the string until you reach a critical moment, resulting in two new mesons. The string model was interesting for this reason, but predicted a number of strange things that didn’t appear to match reality, such as a spin-2 boson (which wasn’t observed), the fact that the spin-1 state doesn’t become massive during symmetry breaking (i.e., there’s no Higgs mechanism), and the need for either 10 or 26 dimensions.

Then the idea of asymptotic freedom was discovered and the theory of quantum chromodynamics (QCD) came to be, and the string model fell out of favor. QCD described the strong nuclear force and interactions extraordinarily well without these pathologies, and the idea was abandoned. The Standard Model, now complete, didn’t need this new, esoteric, and simultaneously ineffective framework.

At high energies (corresponding to small distances), the strong force’s interaction strength drops to zero. At large distances, it increases rapidly. This idea is known as ‘asymptotic freedom,’ which has been experimentally confirmed to great precision. (S. BETHKE; PROG.PART.NUCL.PHYS.58:351–386,2007)

But a decade or so later, this idea was reborn into what’s now known as modern string theory. Instead of working at the energy scales where nuclear interactions are important, the idea was put forth to take the energy scale all the way up to the Planck energy, where the spin-2 particle that made no sense could now play the role of the graviton: the theoretical force-carrying particle responsible for a quantum theory of gravity. That spin-1 particle could be the photon, and other excited states could be associated with the known Standard Model particles.

All of a sudden, a long sought dreamed seemed within reach in this new framework. For one, string theory suddenly made it plausible that the Standard Model of particles and interactions could be reconciled with General Relativity. By viewing each of the elementary particles as either an open or closed string that vibrated at specific, unique frequencies, and the fundamental constants of nature as various states of the vacuum in string theory, physicists could finally hope to unify all the fundamental forces together.

Feynman diagrams (top) are based off of point particles and their interactions. Converting them into their string theory analogues (bottom) gives rise to surfaces which can have non-trivial curvature. In string theory, all particles are simply different vibrating modes of an underlying, more fundamental structure: strings. (PHYS. TODAY 68, 11, 38 (2015))

But what you get out of string theory isn’t exactly as simple as this. You don’t simply get the Standard Model and General Relativity, but rather something much, much larger and more grandiose that contains both the Standard Model and General Relativity, but also much more.

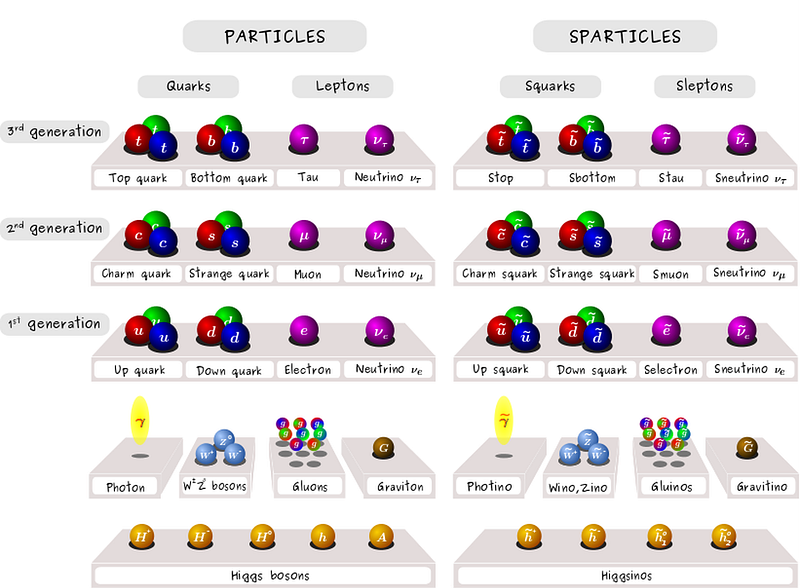
For one, string theory doesn’t simply contain the Standard Model as its low-energy limit, but a gauge theory known as N=4 supersymmetric Yang-Mills theory. Typically, the supersymmetry you hear about involves superpartner particles for every particle in existence in the Standard Model, which is an example of an N=1 supersymmetry. String theory, even in the low-energy limit, demands a much greater degree of symmetry than even this, which means that a low-energy prediction of superpartners should arise. The fact that we have discovered exactly 0 supersymmetric particles, even at LHC energies, is an enormous disappointment for string theory.

The Standard Model particles and their supersymmetric counterparts. Slightly under 50% of these particles have been discovered, and just over 50% have never showed a trace that they exist. Supersymmetry is an idea that hopes to improve on the Standard Model, but it has yet to make successful predictions about the Universe in attempting to supplant the prevailing theory. If there is no supersymmetry at all energies, string theory must be wrong. (CLAIRE DAVID / CERN)

For another, string theory, even in “only” 10 dimensions, doesn’t give you General Relativity as your theory of gravity, but rather a 10-dimensional Brans-Dicke theory of gravity. You can get General Relativity out of that, but only if you take the Brans-Dicke coupling constant (ω) to infinity and somehow remove 6 of those dimensions from relevance.

If you’ve ever heard the word “compactification” used in the context of string theory, this is what it means: a hand-waving suggestion that somehow, these extra dimensions and that additional parameter (ω) become unimportant. String theory, on its own, doesn’t offer a compelling way to get rid of these extra dimensions or to make the Brans-Dicke parameter unimportant. And it must be unimportant; the original work that Brans and Dicke put forth suggested that a ω of around 5 might be interesting; modern tests of relativity have shown it must be greater than ~10,000 or so.

A 2-D projection of a Calabi-Yau manifold, one popular method of compactifying the extra, unwanted dimensions of String Theory. The Maldacena conjecture says that anti-de Sitter space is mathematically dual to conformal field theories in one fewer dimension. This may not hold any relevance for the physics of our Universe. (WIKIMEDIA COMMONS USER LUNCH)

String theory also doesn’t tell you what the values fundamental constants ought to have, since it offers no concrete way to calculate these string vacua that give rise to the fundamental constants. This includes c, the speed of light, h, Planck’s constant, G, the gravitational constant, the coupling constants for the forces, the masses of the fundamental particles, the mixing angles of quarks and neutrinos, and the cosmological constant. String theory offers no clues towards calculating these fundamental values.

However, the potential of string theory to even offer a possible quantum theory of gravity was what drew the majority of theoretical physicists to it, and the lack of solid alternatives have kept the field there. Despite the existence of four quantum gravity alternatives:

loop quantum gravity,
asymptotically safe gravity,
causal dynamical triangulations,
and entropic gravity,

only string theory legitimately offers a true path, where all of the Standard Model is unified with gravity, to that holy grail.

Whether the expansion of the Universe accelerates or decelerates depends not only on the energy density of the Universe (ρ), but also on the pressure (p) of the various components of energy. For something like dark energy, where the pressure is large and negative, the Universe accelerates, rather than decelerates, over time. String theory, requiring anti-de Sitter space, predicts a cosmological constant of the wrong sign to match our observations of dark energy. (NASA & ESA / E. SIEGEL)

However, the field is rife with problems. The correspondence between the aforementioned N=4 supersymmetric Yang-Mills theory and a string in a higher-dimensional space is one of the biggest theoretical breakthroughs touted in string theory, and yet the “space” that it corresponds to is anti-de Sitter space (AdS), which predicts a cosmological constant with the wrong sign (negative instead of positive) to agree with observations of our Universe.

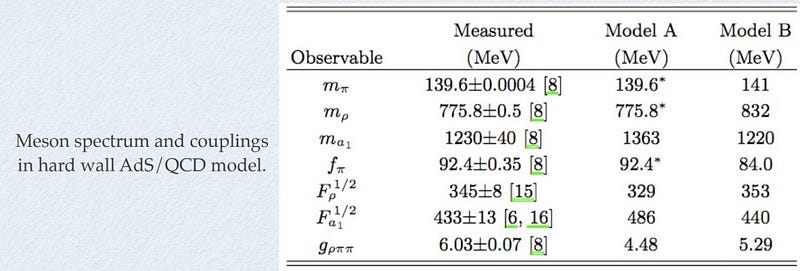
There are a number of insights that string theory has offered into the problem of black hole entropy, but many argue that these have largely been oversold, and that we don’t understand entropy for black holes nearly as well as we claim to. And when you look at the explicit predictions that have come out for the masses of the mesons that have been already discovered, by using lattice techniques, they differ from observations by amounts that would be a dealbreaker for any other theory.

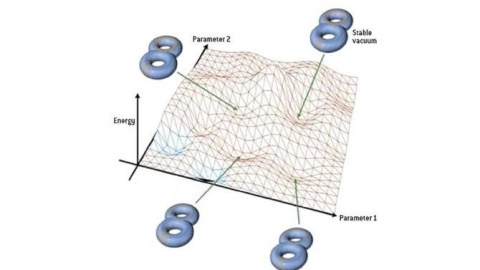
The actual masses of a number of observed mesons and quantum states, at left, compared with a variety of predictions for those masses using lattice techniques in the context of string theory. The mismatch between observations and calculations is an enormous challenge for string theorists to account for. (JEFFREY HARVEY (2010))

Still, there are a large number of people who are drawn in by the mathematical allure of the theory. It incorporates concepts from quantum field theory, supersymmetry, grand unification theories, supergravity, extra dimensions and General Relativity all in a single framework. Originally, there were many different string theories proposed, but mathematical advances have shown that they are all equivalent, or dual, to one another.

However, every turn where we have looked for an observable that might be connected to string theory, in the sense that it would go beyond the Standard Model, we’ve come up empty. The cosmological constant is the wrong sign. Supersymmetric particles are nowhere to be found. Extra dimensions or a non-infinite Brans-Dicke parameter have no evidence to support them. And the fundamental constants, as well as the masses of the particles that exist in our Universe, have not been successfully predicted.

The idea that the forces, particles and interactions that we see today are all manifestations of a single, overarching theory is an attractive one, requiring extra dimensions and lots of new particles and interactions. The lack of even a single verified prediction in string theory, combined with its inability to even give the right answer for parameters whose value is already known, is an enormous drawback of this brilliant idea. (WIKIMEDIA COMMONS USER ROGILBERT)

The problem, as many see it, is that string theory was a very good idea, and people have a hard time abandoning good ideas no matter how fruitless their pursuit has been. Even though it didn’t work out as a theory of the strong interactions, it provided the germ of what could become the holy grail of modern physics: a theory of quantum gravity that unifies General Relativity with the Standard Model.

So long as we don’t have evidence that demonstrates string theory must be wrong, people will continue to pursue it. But disproving it would require something like demonstrating that no superparticles exist all the way up to the Planck scale, something far beyond the reach of experimental physics today.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

We can all agree that string theory is interesting for the possibilities it holds. Whether those possibilities are relevant or meaningful for our Universe, however, is something science has yet to affirm.

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.