Why is the Universe fundamentally left-handed?


The weak interactions only couple to left-handed particles. And we still don’t know why.
When you wave at yourself in a mirror, your reflection waves back. But the hand your reflection waves back with is the opposite hand from the one you’re waving with. This doesn’t pose a problem for most of us, since we could just as easily have chosen the opposite hand to wave with, and our reflection then would have waved back with its opposite hand as well. But for the Universe — and in particular, for any particle experiencing an interaction through the weak force — some interactions only occur for the left-handed version. The right-handed versions, despite our best efforts to locate them, simply don’t exist.
But why? Why does the Universe have this property, and why does it only show up for the weak interactions, while the strong, electromagnetic, and gravitational interactions are all perfectly symmetric between left-handed and right-handed configurations? It’s a fact that’s been scientifically demonstrated empirically in numerous ways, with new experiments poised to test this assumption even further. Even though it’s well-described by the physics of the Standard Model, no one knows why the Universe is this way. Here’s what we know so far.

Imagine, instead of a human being, that you were a particle instead. You’re moving through space; you have certain quantum properties like mass and charge; and you not only have an angular momentum with respect to all the particles (and antiparticles) around you, but an intrinsic angular momentum with respect to your direction-of-motion, known as spin. The specific quantum properties that you have, as a particle, determine and define exactly what you are.
You can imagine both left-handed and right-handed versions of yourself by using your hands. Start by taking your thumbs and pointing them in the same direction: any direction you choose, but the same direction as one another. Now, curl your fingers around the direction your thumb points. If you look head-on to your thumbs, as though your thumbs were coming “towards” you, you’d be able to see the difference in spin: the left-handed particles all spin clockwise, while the right-handed particles all spin counterclockwise.
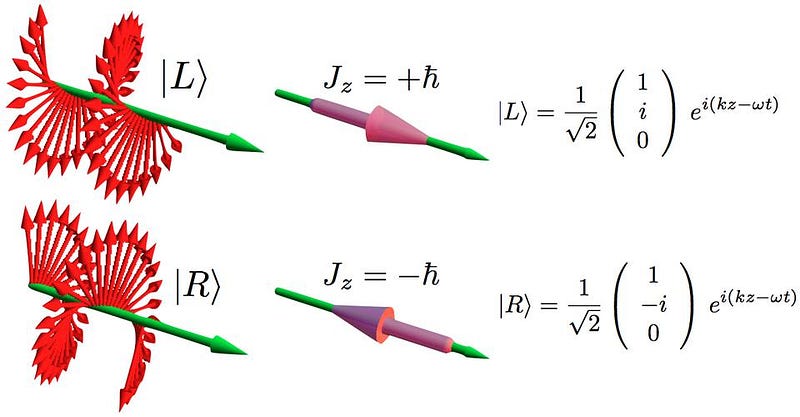
Most of the time, physics doesn’t care which way you’re spinning; the laws and rules are the same. A spinning top obeys the same laws of physics whether it spins clockwise or counterclockwise; a planet that spins on its axis obeys the same rules whether it spins in the same or the opposite direction to its orbit; a spinning electron that cascades down to a lower energy level in an atom will emit a photon irrespective of which direction the electron spins in. Under most circumstances, the laws of physics are what we call left-right symmetric.
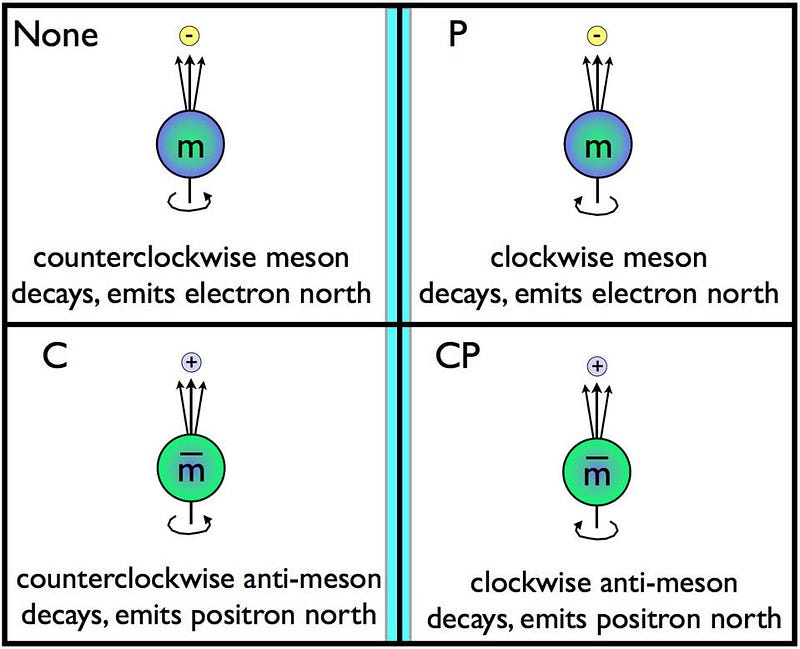
This “mirror symmetry” is one of the three fundamental classes of symmetries we can apply to particles and the laws of physics. In the early half of the 20th century, we thought that there were certain symmetries that were always preserved, and three of them were:
- parity (P) symmetry, stating that the laws of physics are the same for all particles as they are for their mirror-image reflections,
- charge conjugation (C) symmetry, where the laws of physics are the same for particles as they are for antiparticles,
- and time-reversal (T) symmetry, which states that the laws of physics are the same if you view a system going forwards in time versus one going backwards in time.
Under all the classical laws of physics, as well as General Relativity and even quantum electrodynamics, these symmetries are always preserved.
But if you want to know whether the Universe is truly symmetric under all of these transformations, you have to test it in every way imaginable. We got our first hint that something might not be right with this picture in 1956: the year we experimentally discovered the neutrino. This particle was proposed way back in 1930 by Wolfgang Pauli, as a tiny, neutral, novel quantum that could carry energy away during radioactive decays. Upon its proposal, the eminently quotable Pauli lamented,
“I have done a terrible thing, I have postulated a particle that cannot be detected.”
Because neutrinos were predicted to have such a minuscule cross-section when it came to interacting with normal matter, Pauli could not envision a realistic way to detect them when he first proposed them. But decades later, scientists had not only mastered the splitting of the atom, but nuclear reactors had become commonplace. These reactors — under Pauli’s proposal — should be producing the neutrino’s antimatter counterpart in great abundance: the antineutrino. By constructing a detector right next to a nuclear reactor, the first antineutrino detection occurred in 1956, 26 years later.

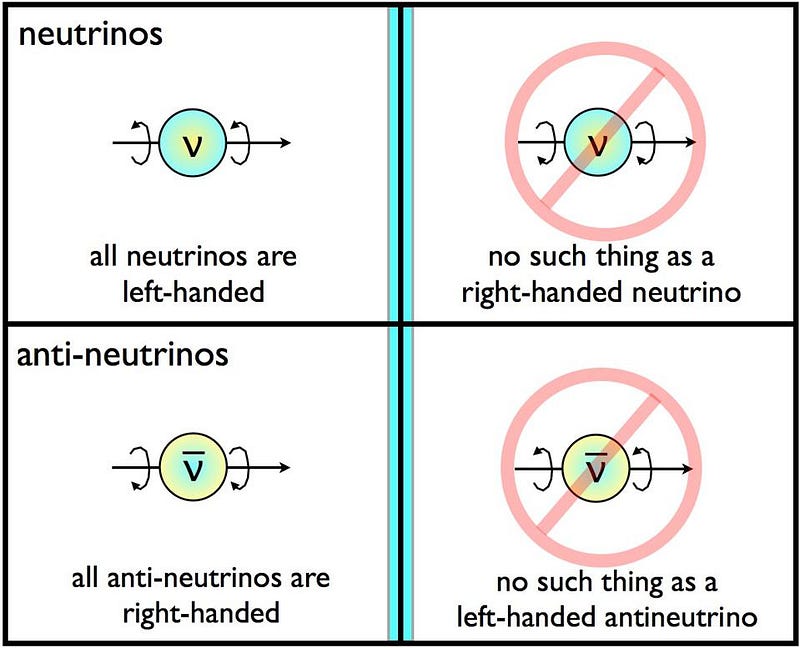
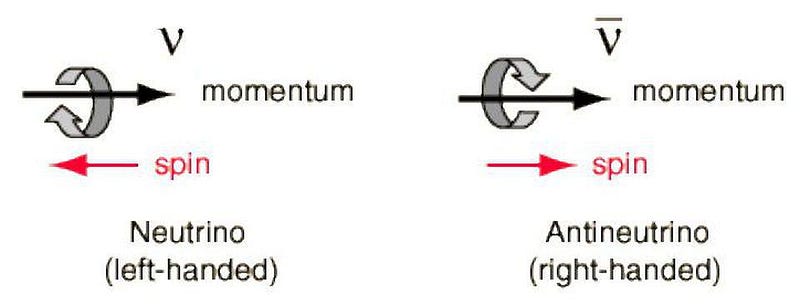
However, something interesting was noticed about these antineutrinos: every single one of them was right-handed, with its spin pointing counterclockwise if you looked “towards” its direction of motion. Later on, we began to detect neutrinos as well, and discovered that every single one of them was left-handed, with its spin oriented clockwise when its direction of motion is towards you.
This might seem like an impossible measurement to make, at first glance. If neutrinos (and antineutrinos) are so difficult to measure that they only interact with another particle extremely rarely, then how can we measure their spins?
The answer is that we don’t learn their spins from directly measuring them, but rather by looking at the particles that come out in the aftermath of an interaction, as well as their properties. We do this for all particles we can’t directly measure, including the Higgs boson, presently known to be the only fundamental particle to have a spin of 0.
How do we do this?
The Higgs sometimes decays into two photons, which can have a spin of +1 or -1. When you measure the photons, that tells you that the Higgs has a spin of either 0 or 2, because you can add or subtract those photon spins to get either 0 or 2. On the other hand, the Higgs sometimes decays into a quark-antiquark pair, with each quark/antiquark having a spin of +½ or -½. By adding or subtracting those spins, we can get either 0 or 1. With one measurement alone, we wouldn’t learn the spin of the Higgs boson, but with all of these measurements combined, only 0 remains as a viable option for its spin.
Similar techniques were used to measure the spin of the neutrino and the antineutrino, and — quite surprisingly to most — they’ve revealed a Universe that isn’t the same in the mirror as it is in our reality. If you put a left-handed neutrino in the mirror, it would appear right-handed, just as your left hand appears to be a right hand in the mirror. But there are no right-handed neutrinos in our Universe, nor are there left-handed anti-neutrinos. For some reason, the Universe cares about handedness.
How do we make sense of this?
The theorists Tsung Dao Lee and Chen Ning Yang put forth the idea of parity laws, and showed that while parity appeared to be an excellent symmetry that was conserved for the strong and electromagnetic interactions, it hadn’t been adequately tested in — and might therefore be violated by — the weak interactions. Weak interactions are any interaction that involve a decay where one particle type transforms into another, such as a muon becoming an electron, a strange quark becoming an up quark, or a neutron decaying into a proton (as one of its down quarks decays into an up quark).
If parity were conserved, then the weak interactions in general (and every weak decay, in particular) would couple equally to both left-handed and right-handed particles. But if parity were violated, perhaps the weak interaction would only couple to left-handed particles. If only there were an experimental way to tell.

In 1956, Chien-Shiung Wu took a sample of cobalt-60, a radioactive isotope of cobalt, and cooled it down close to absolute zero. Cobalt-60 was known to decay into Nickel-60 via beta decay: the weak decay transforms one of the nucleus’s neutrons into a proton, emitting an electron and an antineutrino in the process. By applying a magnetic field to the cobalt, she could get all of the cobalt-60 atoms to line up along the same spin axis.
If parity were conserved, then you’d be just as likely to see the electrons — also known as beta particles — emitted aligned with the spin-axis as you would be to see them anti-aligned with the spin-axis. But if parity were violated, the emitted electrons would be asymmetric. In a monumental result, Wu demonstrated that not only were the emitted electrons asymmetric, but they were about as maximally asymmetric as theoretically possible. A few months later, Pauli wrote to Victor Weisskopf, stating,
“I cannot believe that God is a weak left-hander.”
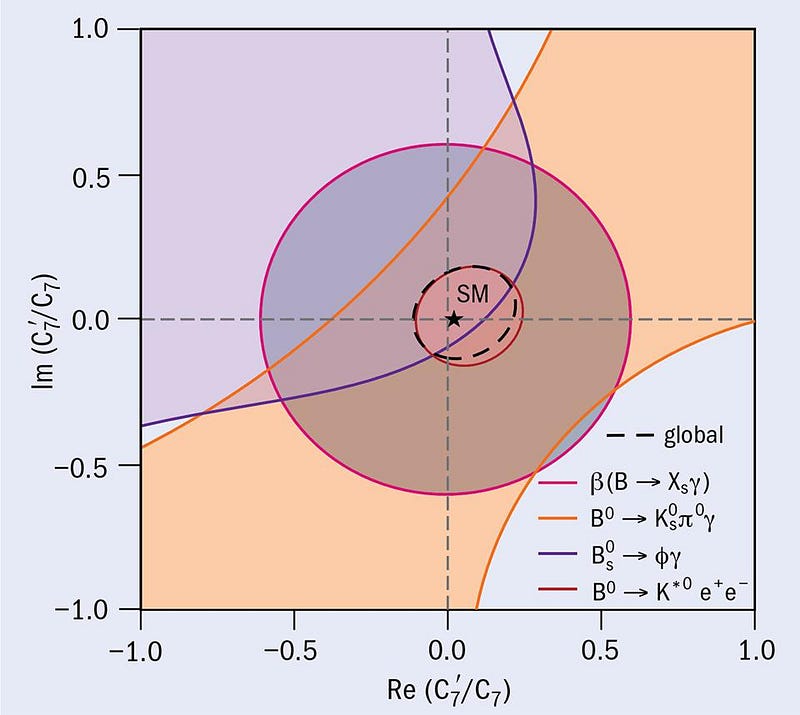
But the weak interaction does only couple to left-handed particles, at least, as far as we’ve measured it. This brings up an interesting question about something we haven’t measured: when photons get involved in the weak interaction, do both left-handed and right-handed photons play a role, or only the left-handed ones? For instance, you can have a bottom (b) quark transform into a strange (s) quark in the weak interactions, which normally occurs without a photon as part of the mix. However, even though it’s suppressed, a tiny fraction of b-quarks will transform into an s-quark with an extra photon: fewer than 1-in-1000. Although rare, this can be studied.
According to expectations, that photon should always be left-handed: consistent with how we expect parity to work (and be violated for the weak interactions) in the Standard Model. But if the photon is even sometimes allowed to be right-handed, we could find another crack in our current understanding of physics. Certain predicted decays could:
- show a surprising photon polarization,
- have different rates over what was predicted,
- or could show a charge-parity (CP) asymmetry.
The LHCb collaboration at CERN is the best place on Earth to study this possibility, and they’ve just placed the strongest constraint ever on the absence of right-handed photons. If the graph, below, ever improves to the point where the central point, (0,0), is excluded, that would mean we’ve discovered new physics.
It’s eminently true that we can describe the Universe as being perfectly symmetric between mirror-reflections, replacing particles with antiparticles, and interactions going forwards or backwards in time, for every force and interaction that we know of, except one. In the weak interactions and the weak interactions alone, however, none of these symmetries are conserved. As far as the weak interactions are concerned, every measurement we’ve ever made shows that Pauli would still be in disbelief today: more than 60 years after parity violation was first discovered, the weak interaction has still been shown to couple exclusively to left-handed particles.
Because neutrinos have mass, one of the most remarkable experiments to perform would be to travel extremely close to the speed of light: overtaking a left-handed neutrino so that its spin would appear to reverse from your perspective. Would it suddenly display the properties of a right-handed antineutrino? Would it be right-handed, but still behave as a neutrino? Whatever its characteristics, it might reveal new information about the fundamental nature of our Universe. Until that day arrives, indirect measurements — such as the ones happening at CERN and the searches for neutrinoless double beta decay — will be our best opportunity for discovering whether our Universe isn’t as left-handed as we presently think.
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





