Ask Ethan: Why do galaxies spin?

For every phenomenon we observe in the Universe, there’s some underlying cause that ought to explain its behavior. Given the laws of physics, the fundamental objects that exist, and the way that they assemble based on the interactions between them, we should be able to derive solid, robust predictions that agree with the Universe we see today. In other words, for every effect that we see, the quest of science is to understand the cause of that effect. Sometimes, however, this is easier said than done. Certain effects, like the matter-antimatter asymmetry, the gravitational behavior of large-scale cosmic structure, and the accelerated expansion of the Universe are all well-established, but their underlying cause remains obscure.

But some phenomena truly can be explained, scientifically, even if the explanation isn’t immediately apparent. Maynard Falconer writes in with precisely such a question, asking:

“Angular [momentum] is one of the fundamentals that needs to be conserved and is [a] major component in determining the shape of large and small cosmic structures. Did the universe start with [a] net angular momentum of zero? What is the relationship between angular momentum… and galaxies, galaxies and their solar systems, solar systems and the various bodies inside of them, etc.?”

These are great questions, and the cosmic story we’ve put together can put it all in context. Let’s start at the beginning and dive in!

The quantum fluctuations inherent to space, stretched across the Universe during cosmic inflation, gave rise to the density fluctuations imprinted in the cosmic microwave background, which in turn gave rise to the stars, galaxies, and other large-scale structures in the Universe today. This is the best picture we have of how the entire Universe behaves, where inflation precedes and sets up the Big Bang. Unfortunately, we can only access the information contained inside our cosmic horizon, which is all part of the same fraction of one region where inflation ended some 13.8 billion years ago.

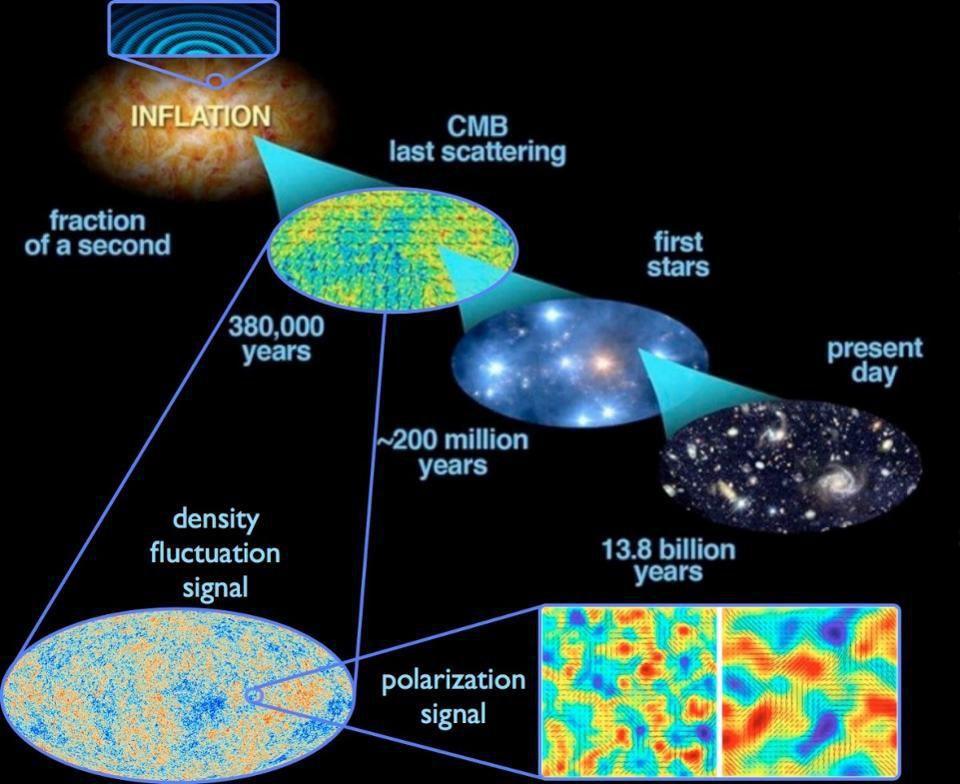
Before the hot Big Bang took place, a period of cosmic inflation occurred: stretching the Universe flat, creating uniform conditions everywhere, and imprinting a series of small-magnitude fluctuations on all cosmic scales. These fluctuations include density imperfections, gravitational wave imperfections, and also angular momentum imperfections. Yes, that’s right: when the hot Big Bang first occurred, it wasn’t just born with the seed fluctuations that would lead to the growth of stars, galaxies, and the large-scale structure of the Universe, but it was born with an intrinsic amount (and distribution) of angular momentum, too.

But then something happens: the Universe expands. Certain types of imperfections grow in the expanding Universe — like density fluctuations — while other types of imperfections decay. The seeds of angular momentum fall into the latter category, and it’s easy to visualize. You’re all familiar with a figure skater spinning around and then pulling their arms and legs in, spinning up and rotating faster in the process. Well, the expanding Universe is exactly the opposite of that: whatever angular momentum you start with, the act of expansion pushes the mass away from your center, causing you to rotate slower and slower. Eventually, regardless of what angular momentum you began with, your spin and/or rotational motion becomes negligible.

When a figure skater like Yuko Kavaguti (pictured here from 2010’s Cup of Russia) spins with her limbs far from her body, her rotational speed (as measured by angular velocity, or the number of revolutions-per-minute) is lower than when she pulls her mass close to her axis of rotation. The conservation of angular momentum ensures that as she pulls her mass closer to the central axis of rotation, her angular velocity speeds up to compensate.

But you shouldn’t forget about it entirely! Over time, the growing density imperfections will eventually cross a critical threshold due to gravitational growth: they’ll lead to the overdense regions becoming about ⅔ denser than the overall cosmic average density. Whenever a region crosses that density threshold, it becomes gravitationally bound, and not only starts to contract — overcoming the cosmic expansion — but it begins to pull in more and more matter from the surrounding regions. It’s well on its way to forming stars and growing into a proto-galaxy or even a larger cosmic structure.

When that occurs, two things begin to happen.

1. Remember that initial angular momentum that it was “born” with? Well, now that this mass is contracting after expanding, it’s starting to spin up and increase its rotation rate again. That initial angular momentum didn’t go away, and now, as it shrinks down, it has a chance to become important again.
2. And the other masses in the Universe, particularly the nearby overdense and underdense regions, exert tidal forces on it. The “nearer” side to the mass experiences a greater gravitational force than the “farther” side from the mass, and this can not only stretch the object, but can cause a torque: leading to an angular acceleration and a net rotation.

Although the Sun orbits within the plane of the Milky Way some 25,000-27,000 light years from the center, the orbital directions of the planets in our Solar System do not align with the galaxy at all. As far as we can tell, the orbital planes of the planets occur randomly within a stellar system, often aligned with the central star’s rotational plane but randomly aligned with the plane of the Milky Way, as local torques from nearby masses can swamp the effects provided by the overall galactic rotation.

In fact, this “tidal torque” phenomenon is one of the most likely culprits of the origin of how individual galaxies and stellar systems acquire their spins and net angular momenta. Whenever a large object passes close by another mass, the tidal forces actually get stronger more quickly than the gravitational forces do. Gravity, remember, is a ~1/r² force, at least according to Newton. (And only in very strong gravitational fields is it different, even according to Einstein.) That means if you bring a mass closer to an object — to 10%, 1% or 0.1% of the original distance — the gravitational force becomes a hundred, ten thousand, or even a million times as strong as the original gravitational force.

But tidal forces obey a different rule: they behave as a ~1/r³ force. That means they become less important at large distances compared to the gravitational force, which is why even though the Sun is 27 million times more massive than the Moon, the Moon’s tidal forces on Earth are about three times the strength of the Sun’s. That closer distance is tremendously important. When you bring a mass closer to an object — to 10%, 1% or 0.1% of the original distance — the tidal force acting upon the object becomes a thousand, a million, or even a billion times as strong as the original tidal force.

The M81 triplet, consisting of M81 (right-center), M82 (top) and NGC 3077 (left) are all connected by a vast bridge of neutral hydrogen. Gas infall, star formation, and gravitational tidal effects are all related, with the strength of tidal forces increasing much more rapidly with shorter distances than even the gravitational force.

In what I’ll call “messy” astrophysical environments, where there are lots of dense clumps of matter acting at short distances on one another, tidal torques can quickly transform a series of systems that aren’t rotating into a set where every single system has an overall, net rotation. This plays an especially strong role in stellar nurseries and star-forming regions, where new stars and stellar systems are being born.

Take a cloud of gas, make it massive enough, let it cool, and watch it gravitationally collapse. As the collapse begins, it will start to fragment into individual regions, some with greater amounts of mass and higher densities and others with lesser amounts of mass and lower densities. The highest density, highest mass regions will collapse first, forming what you can visualize as a massive potato-shaped object: a three-dimensional irregular structure, where one axis is the longest and another axis is the shortest.

Gravitational collapse always proceeds fastest along the shortest direction, and when that occurs, you get a “splat,” or what astrophysicists call a pancake. In the aftermath of this pancaking, there’s always a circumstellar disk surrounding the largest, densest mass(es): the protostar(s).

This two-toned image shows an illustration of the protoplanetary disk around the young star FU Orionis, which was imaged multiple times by the Hubble Space Telescope but years apart. The disk has changed, indicating that it’s entering a more advanced stage of evolution, as planets form and the material available for forming and growing them evaporates, sublimates, and is otherwise blown away. Planets and the central star are all expected to orbit and rotate in the same direction; only collisions and interactions should change that story.

Even a tiny amount of initial angular momentum — which every such proto-stellar system acquires — is enough to ensure that each protoplanetary disk comes along with a net angular momentum, and this leads to a mature stellar system where, overall, there’s a preferred direction for the mature star, planets, and moons that arise to all move in. In particular:

• the star will have a preferred axis and direction of rotation,
• the planets will preferentially orbit around the star in that same direction,
• the moons of those planets will preferentially orbit around each planet in that same direction,
• each planet will rotate around its axis in that same direction,
• and the only exceptions will arise from collisions, mergers, or gravitational interactions between objects or proto-objects within that same stellar system.

We see the evidence of this in exoplanetary systems, in protoplanetary disk systems, and even in our own Solar System, where the only exceptions are the rotations of Venus and Uranus (which were likely knocked over by collisions) and moons that arose via gravitational capture, like Neptune’s Triton or Saturn’s Phoebe.

Phoebe’s pumice-like appearance and counter-rotation can only be explained if it originated from the outer Solar System: beyond where the gas giants lie. Iapetus, however, the Saturnian moon darkened by Phoebe’s particles, is more consistent with an origin similar to the other major moons of Saturn, as it orbits in the same prograde direction as the other moons and planets of the Solar System.

The orientations of stellar systems have, as far as we can tell, very little to do with the overall angular momentum of the galaxies they’re born into; the local dynamics of clumps of matter and the tidal torques arising from them are sufficiently large — in both simulations and via observations — that they can overcome any initial impetus from the overall galaxy as a whole.

Meanwhile, galaxies themselves, in dense environments such as galaxy clusters, experience an analogous phenomenon. The closer you get to the cluster center, the more likely you are to find a spiral or disk galaxy in a completely random orientation. Additionally, as galaxies merge and interact in these dense environments, they become more and more likely to transform into elliptical galaxies, where the smooth, overall spiral structure is instead destroyed, replaced with a random “swarm” of stars within it, moving chaotically like bees surrounding a beehive. When we look at the central regions of the densest galaxy clusters, they’re not only dominated by giant ellipticals, but the spirals and other disk galaxies are completely randomly oriented, as opposed to small satellite galaxies around isolated large ones, which preferentially cluster in a plane.

The Coma Cluster of galaxies, as seen with a composite of modern space and ground-based telescopes. The Coma Cluster, the largest galaxy cluster in our nearby Universe, is dominated by two giant elliptical galaxies, with over 1000 other spirals and ellipticals inside. The speed of the individual galaxies within the Coma Cluster is too great for the cluster to remain a bound entity based on its normal matter content alone. It can only remain a bound object under Einstein’s laws of General Relativity if a substantial amount of additional matter, i.e., a source of dark matter, exists throughout this cluster. The total mass of the cluster comes in at a few quadrillion solar masses.

But on large cosmic scales outside of these dense cluster environments, you might wonder if the large-scale structure of the Universe has any effects on the orientation of galaxies that arise. After all, there’s a twofold way that cosmic structure can form, and both influences can matter depending on circumstances and initial conditions: top-down and bottom-up.

Bottom-up structure formation occurs when objects first form on small cosmic scales, and then merge together, interact, and build up to form structure on progressively larger scales. Top-down structure formation, by contrast, occurs when the larger-scale cosmic structures form, and then fragment into smaller components, with the smaller-scale structures maintaining a memory or imprint from the larger-scale structures that they’re derived from.

The messier your environment is, the greater the impact of bottom-up formation is. But when your environment is more pristine — i.e., when there are fewer clumps of matter to interact on smaller scales — you’re much more likely to be influenced by top-down formation. And the largest structures of all arise from the cosmic web, along giant, dark-matter-dominated filaments.

This image shows a 15 million light-year long structure that arises from a detailed simulation of the cosmic web and how galaxies, galaxy clusters, and cosmic filaments form on the largest scales of all. Although this theoretical simulation, like many aspects of our standard cosmological models, largely agrees with our observations, the smaller-scale features that arise, like the spins of individual galaxies, cannot be determined without observational inputs as well.

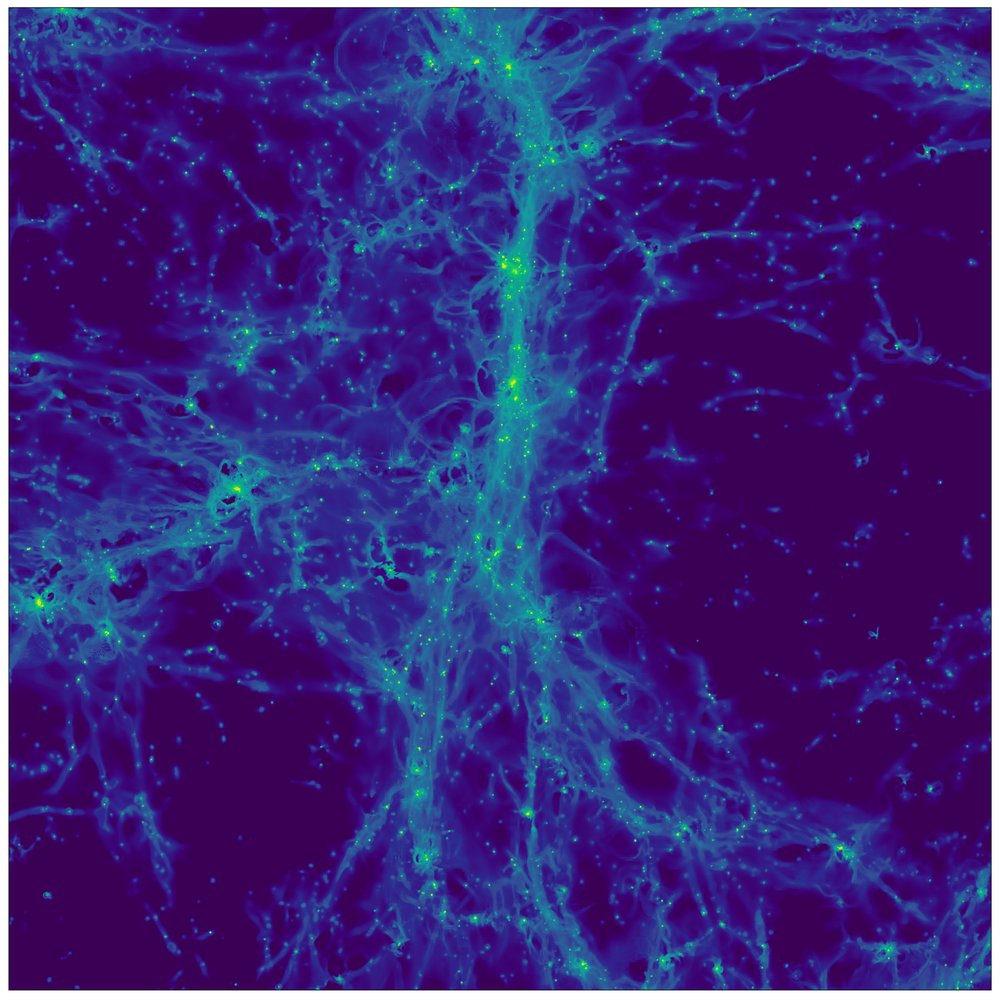
Do these filaments have any sort of influence on the spins and overall rotational orientations of the galaxies that form along them? In a landmark study that just came out in August of 2022, the scientists working on the SAMI galaxy survey concluded that yes, these two phenomena are physically related. What’s remarkable is that galaxies typically have two separate components, the bulge, which is the central portion of the galaxy whose stars exist in a diffuse, elliptical distribution, and the disk, which the most “pancaked” portion of the galaxy that typically rotates in one particular direction.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

What the study found was that, relative to the nearest underlying filament in the cosmic web, these associated galaxies have the following properties.

• Galaxies with small-mass bulges have their spins parallel to the closest filament.
• Galaxies with large-mass bulges have their spins oriented perpendicular to the closest filament.
• And galaxies dominated by disks show a variety of different orientations, related to specific motion-related features and also the mass of the central bulge.

The authors believe that spin-filament alignments are largely driven by the growth of the galactic bulge, as both are underpinned by galactic mergers. The greater the number and severity of mergers, the more massive the bulge will be and the greater the likelihood of a spin-filament alignment flip.

Galaxies can be found along, nearby, and within cosmic filaments. There is often neutral matter within the haloes of these galaxies as well as along their line-of-sights, so when that light arrives, absorption features seen in their spectra reveals the presence of hydrogen, including its normal and deuterated isotopes, can teach us a tremendous amount of information about the Universe.

As an active, ongoing area of research, it’s a bit of a stretch to draw a definitive conclusion as to just what, specifically, causes the angular momentum and rotation of each and every object in the Universe. What we can state, however, is that there are three major effects that are certain to combine to explain most of them.

1. The original angular momentum that the seeds-of-structure in the Universe were born with, which persist and can become important again once that portion of the Universe stops expanding and begins gravitationally contracting and collapsing.
2. The gravitational, tidal interactions between different clumps of matter on small and intermediate cosmic scales, particularly important in dense, rich, chaotic environments.
3. And the larger-scale structures that give rise to and influence the substructures that form within and surrounding them, from galaxies forming along cosmic filaments to planets and moons forming within stellar systems and star clusters.

Any particular system will have its own unique combination of these effects that contribute to its overall, net angular momentum, as well as the rotational and revolutionary properties of each of its components. Still, the general conclusion, that all objects possess angular momentum, is very difficult to avoid. Even though the net angular momentum of the overall Universe is likely negligible, the conclusion that each individual component should have an angular momentum of its own is all but inevitable. Our own Solar System, and all of the objects within it, are merely one typical example that illustrates it in action.

Send in your Ask Ethan questions to startswithabang at gmail dot com!