Why doesn’t antimatter anti-gravitate?

If it’s the anti-version of normal matter, could it possibly fall “up”?
This article was written by Sabine Hossenfelder of Backreaction. Sabine is a theoretical physicist specialized in quantum gravity and high energy physics. She also freelance writes about science.
“If something doesn’t reach you on a personal level, let it go. It’s hard enough dealing with everything that does.” –Judi Culbertson
Why aren’t there any particles that fall upwards in the gravitational field of Earth? It would be so handy — If I had to move the couch, rather than waiting for the husband to flex his muscles, I’d tie an anti-gravitating weight to it and the couch would just float to the other side of the room.
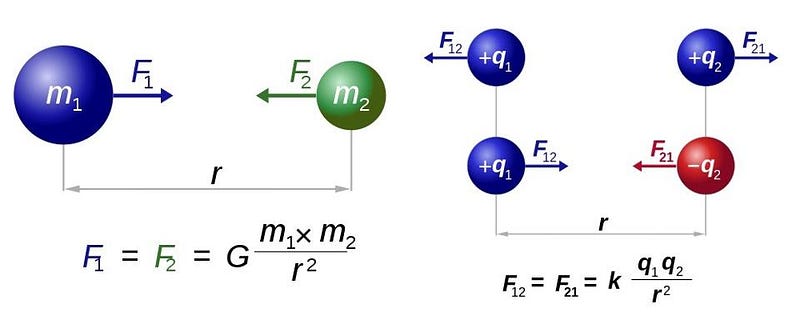
Newton’s law of gravity and Coulomb’s law for the electric force between two charges have the same mathematical form. If you replaced the Coulomb constant with the gravitational one, and charges with masses, they’d be completely identical. So how come we have both positive and negative electric charges but not both negative and positive gravitational masses?
The quick answer to the question is, well, we’ve never seen anything fall up. But if there was anti-gravitating matter, it would be repelled by our planet. If any anti-gravitating matter existed, it would be ejected into space, pushed away from the Sun and even out of our galaxy. So maybe it’s not so surprising we don’t see any of it here. Might there be anti-gravitating matter elsewhere?
It’s a difficult question, more difficult than even most physicists appreciate. The difference between gravity and the electromagnetic interaction — which gives rise to Coulomb’s law — is the type of messenger field. Interactions between particles are mediated by fields. For electromagnetism, the mediator is a vector-field. For gravity, it’s a more complicated field: a 2nd rank tensor-field, which describes space-time itself.
If you quantize an interaction, the interaction’s field is accompanied by a particle. For electromagnetism that’s the photon, for gravity it’s the (hypothetical) graviton. The particles share the properties of the field, but for the question of whether or not there’s anti-gravity the quantization of the field doesn’t play a role.
The major difference between the two cases comes down to a sign. For a vector-field, as in the case of electromagnetism, like charges repel and unlike charges attract. For a 2nd rank tensor field, in contrast, like charges attract and unlike charges repel. This already tells us that an anti-gravitating particle would not be repelled by everything. It would be repelled by normally gravitating mass — which we may agree to call “positive” — but be attracted by gravitational masses of its own kind — which we may call “negative.”
The question then becomes: Where are the particles of negative gravitational mass?

To better understand the theoretical backdrop, we must distinguish between inertial mass and gravitational mass. The inertial mass is what gives rise to an object’s inertia, i.e., its resistance to acceleration. An inertial mass is always positive valued. The gravitational mass, on the other hand, is what creates the gravitational field of the object. In usual general relativity, the two masses are identical by assumption: this is Einstein’s equivalence principle in a nutshell. In more detail, we’d not only talk about the equivalence for all types of masses, but for all types of energies, collected in what is known as the stress-energy-tensor. Again, the details get mathematical very fast, but aren’t so relevant to understand the general structure.
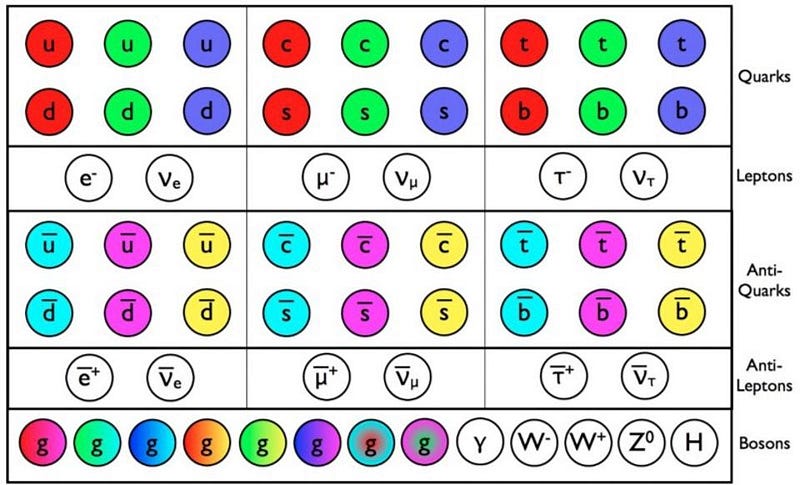
All the particles we presently know of are collected in the standard model of particle physics, which is in agreement with data to very high precision. The standard model also includes all anti-particles, which are identical to their partner-particles except for having opposite electric charge. Is it possible that the anti-particles also anti-gravitate?
Theory clearly answer this question with a resounding, “No.” From the standard model, we can derive how antimatter gravitates — it gravitates exactly the same way as normal matter. And observational evidence supports this conclusion in the following way.

We don’t normally see anti-particles around us because they annihilate when they come in contact with normal matter, leaving behind merely a flash of light. Why there isn’t the same amount of matter and antimatter in the universe nobody really knows — it’s a big mystery that goes under the name “baryon asymmetry” — but evidence shows the universe is dominated by matter. If we see anti-particles — in cosmic rays or in particle colliders — it’s usually as single particles, which are both too light and too short-lived to reliably measure their gravitational mass.
That, however, doesn’t mean we don’t know how antimatter behaves under the influence of gravity. Both matter and antimatter particles hold together the quarks that make up neutrons and protons. Indeed, the anti-particles’ energy makes a pretty large contribution to the total mass of neutrons and protons, and hence to the total mass of everything around us. This means if antimatter had a negative gravitational mass, the equivalence principle would be badly violated. It isn’t, and so we already know antimatter doesn’t anti-gravitate.
Those with little faith in theoretical arguments might want to argue that maybe it’s possible to find a way to make antimatter anti-gravitate only sometimes. I am not aware of any theorem which strictly proves this to be impossible, but neither is there — to my best knowledge — any example of a consistent theory in which this has been shown to work.
And if that still wasn’t enough to convince you, the ALPHA experiment at CERN has not only created neutral anti-hydrogen, made of an anti-proton and a positron (an anti-electron), but has taken great strides towards measuring exactly how anti-hydrogen behaves in Earth’s gravitation field. Guess what? So far there is no evidence that anti-hydrogen falls upwards — though the present measurement precision only rules out that the anti-hydrogen’s gravitational mass is not larger than (minus!) 65 times its inertial mass.

So, at least we theorists are pretty sure that none of the particles we know anti-gravitates. But could there be other particles, which we haven’t yet discovered, that anti-gravitate?
In principle, yes, but there is no observational evidence for this. In contrast to what is often said, dark energy does not anti-gravitate. The distinctive property of dark energy is that the ratio of energy-density over pressure is not only negative, but negative at the right magnitude to cause distant galaxies to accelerate away from one another. For anti-gravitating matter, however, both energy-density and pressure change sign, so that ratio will remain positive. This means anti-gravitating matter, if it exists, behaves just the same way as normal matter does, except that the two types of matter repel each other. It also doesn’t give rise to anything like dark matter, because negative gravitational mass would have the exact opposite effect as needed to explain dark matter.

To be fair, I also don’t know of any experiment that explicitly looks for signatures of anti-gravitational matter, like for example concave gravitational lensing. So, strictly speaking, it hasn’t been ruled out, but it’s a hypothesis that also hasn’t attracted much professional interest, and that no observers have found any signatures for. Many theoretical physicists who I have talked to believe that negative gravitational masses would induce vacuum-decay because particle pairs could be produced out of nothing. This argument, however, doesn’t take into account that the inertial masses remain positive which prohibits pair production. (On a more technical note, it is a little appreciated fact that the canonical stress-energy tensor isn’t the same as the gravitational stress-energy tensor.)
Even so, let us suppose that the theoretically possible anti-gravitating matter is somewhere out there. What would it be good for? Not for much, it turns out. The stuff would interact with our normal matter even more weakly than neutrinos. Unless it also exhibited interactions through one of the other fundamental forces, there’s no realistic experiment that could detect it. This means even if we’d manage to find some of it in our vicinity — which is implausible already — we wouldn’t be able to catch it and use it for anything. It would simply pass right through us.
The anti-gravitating weight that I’d want to tie to the couch, therefore, will unfortunately remain fiction.
This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!