Why are there exactly 3 generations of particles?
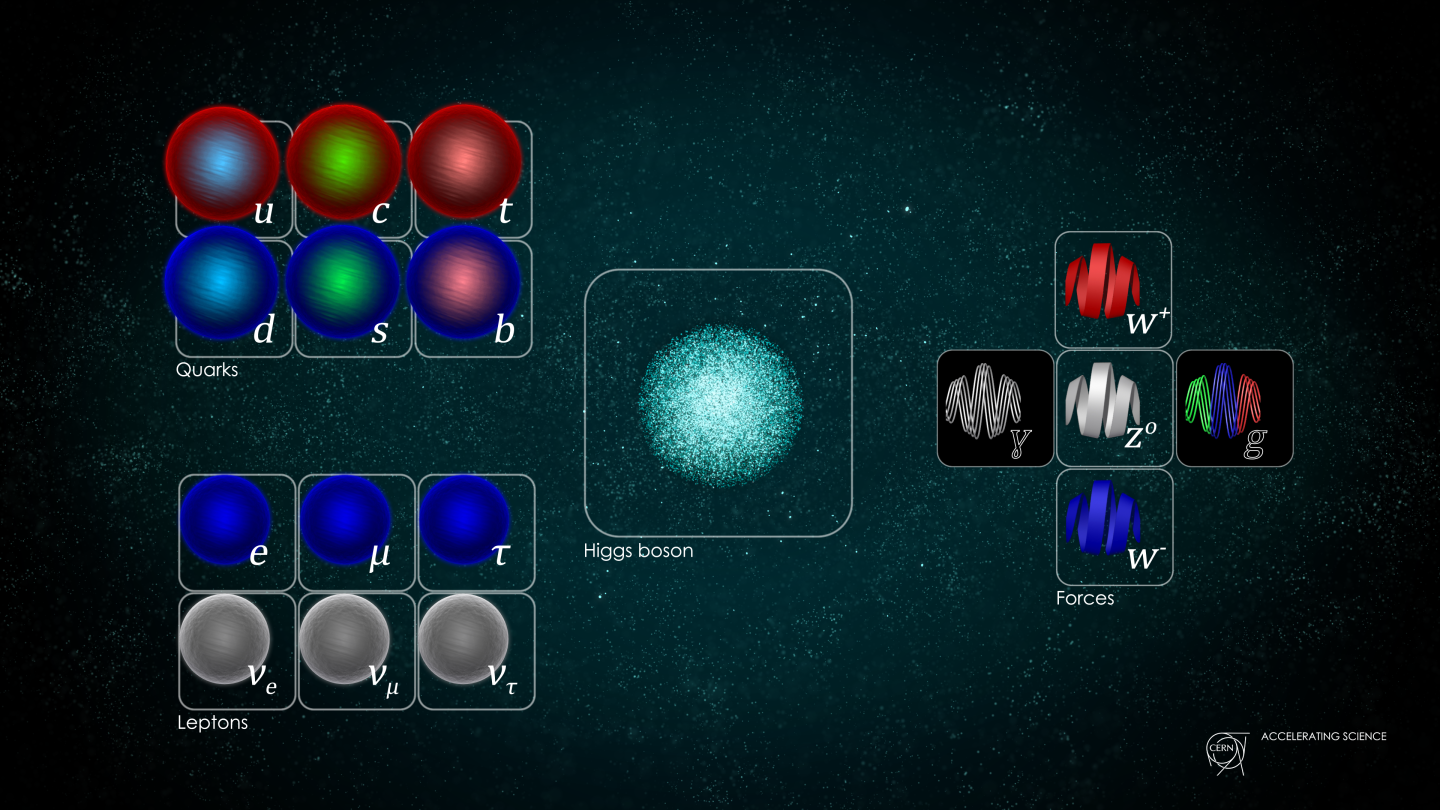
- The Standard Model of elementary particles tells us what the charges, interactions, and other properties of the fundamental particles need to be.
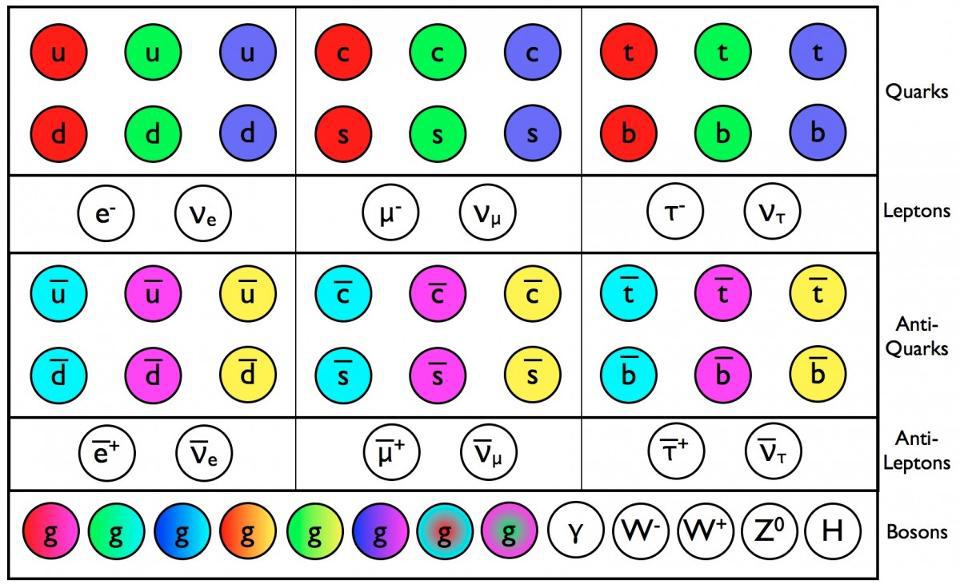
- The number of bosons is fixed: one photon, three heavy weak bosons, and eight massless gluons. But the fermions, coming in both quarks and leptons, come in three sets of nearly-identical “copies.”
- Why are there three generations of particles, rather than fewer or more? Nobody knows for certain. It’s one of the great unexplained mysteries of modern physics.
Everything that exists in our Universe, as far as we understand it, is made up of particles and fields. At a fundamental level, you can break everything down until you reach the limit of divisibility; once things can be divided no further, we proclaim that we’ve landed upon an entity that’s truly fundamental. To the best of our current understanding, there are the known elementary particles — those represented by the Standard Model of elementary particle physics — and then there are the unknowns: things that must be out there beyond the confines of the Standard Model, but whose nature remains unknown to us.
In the latter category are things like dark matter, dark energy, and the particle(s) responsible for creating the matter-antimatter asymmetry in our Universe, as well as any particles that would arise from a quantum theory of gravity. But even within the Standard Model, there are things for which we don’t quite have an adequate explanation. The Standard Model consists of two types of particles:
- the bosons, which mediate the various fundamental forces,
- and the fermions, from which all the normal matter in the Universe is composed.
While there’s only one copy of each of the bosons, for some reason, there are three copies of each of the fermionic particles: they come in three generations. Although it’s long been accepted and robustly experimentally verified, the three-generational nature of the Standard Model is one of the great puzzles of nature. Here’s what we know so far.
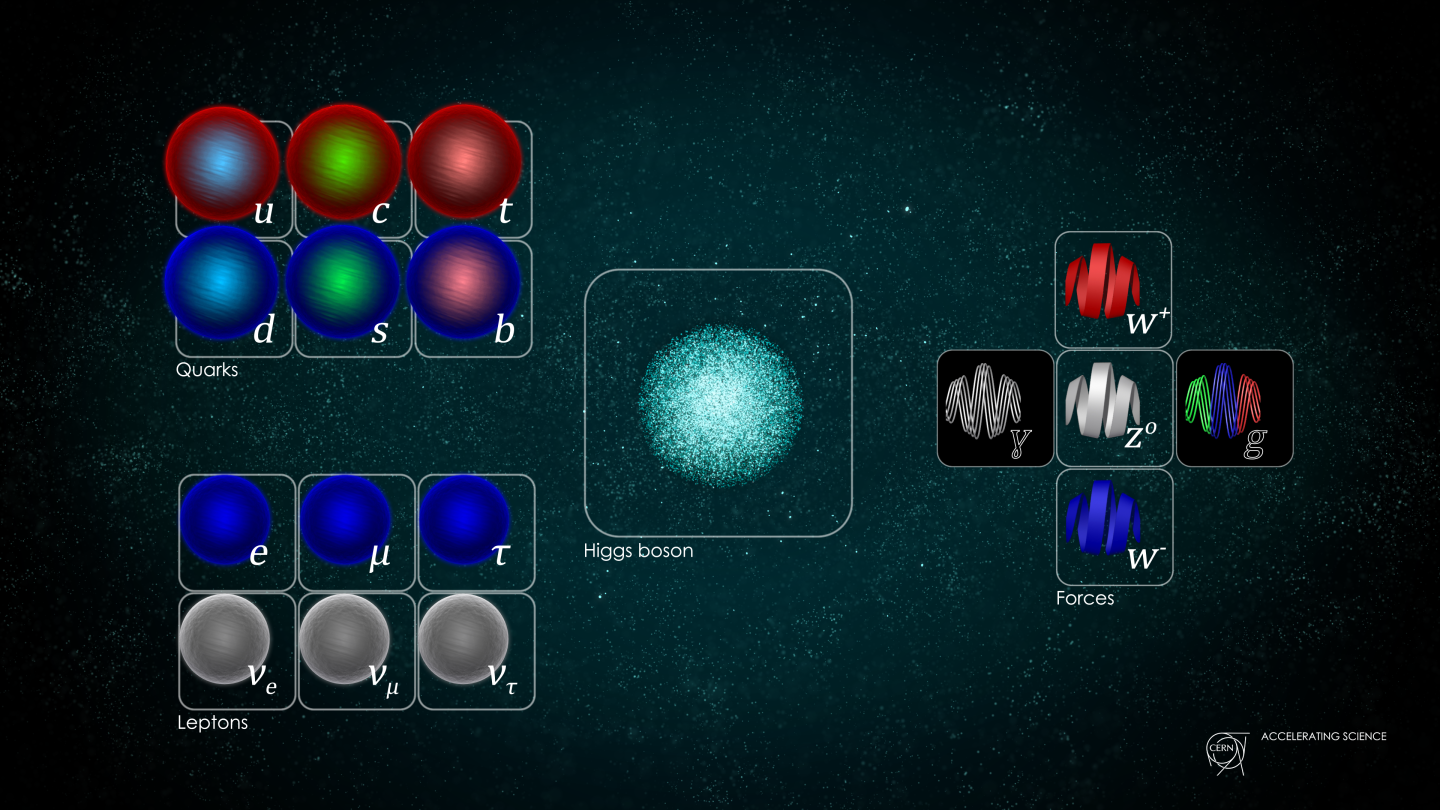
The framework of the Standard Model
Although the Standard Model possesses an incredibly powerful framework — leading to, by many measures, our most successful physical theory of all-time — it also has limitations. It makes a series of predictions that are very robust, but then has a large number of properties that we have no way of predicting: we simply have to go out and measure them to determine just how nature behaves.
- It tells us, for example, that each fermion can be charged or uncharged under each of the three fundamental interactions: electric charge, weak charge (made up of weak isospin and weak hypercharge), and color charge.
- It tells us that there are four types of bosons: the massless photon (mediating the electromagnetic interaction), the three heavy, massive weak bosons (mediating the weak interaction), the eight massless gluons (mediating the strong interaction), and the one Higgs boson.
- It tells us that particles can either have a rest mass of zero, which is the case if they don’t couple at all to the Higgs, or they can have non-zero rest masses, which indicates a positive coupling to the Higgs.
- And it tells us that there will be quarks and leptons (as well as anti-quarks and anti-leptons), all of which couple to the weak interactions. The quarks come with electric charges of +⅔ and -⅓, in each of three different colors, while the leptons come with electric charges of -1 and 0, with no color charge at all.
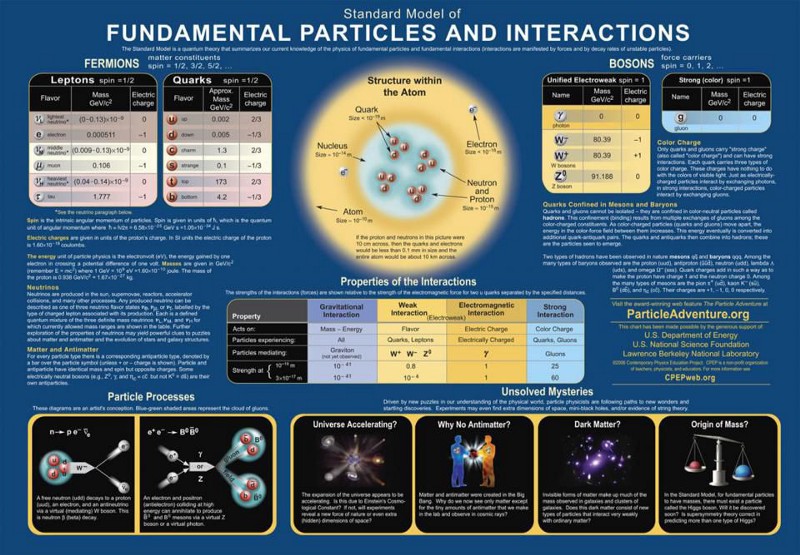
But what the Standard Model doesn’t tell us is also profound.
- It doesn’t tell us what the masses of any of the fundamental particles are; we have to go out and measure them.
- It doesn’t tell us whether the neutrinos are massive or massless; we had to measure their properties to determine that they are, in fact, massive, but with tiny masses compared to the rest of the Standard Model’s massive particles.
- It doesn’t tell us whether there will be multiple copies of the fermions in the Standard Model, how many of those copies there will be, or how the quarks and leptons from different generations will “mix” together.
All of these things can only, at least as we currently understand it, be measured experimentally, and it’s from those experimental results that we can determine the answers.
Fortunately, we’re good enough at experimental particle physics that we’ve been able to determine the answers to these questions through a series of both clever and brute-force observations and experiments. Every single one of the Standard Model’s particles and antiparticles have been discovered, their particle properties have been determined, and the full scope of what exists in the Standard Model — three generations of fermions that are all massive and where quarks of like charges and the massive neutrinos all mix together — is now unambiguous.
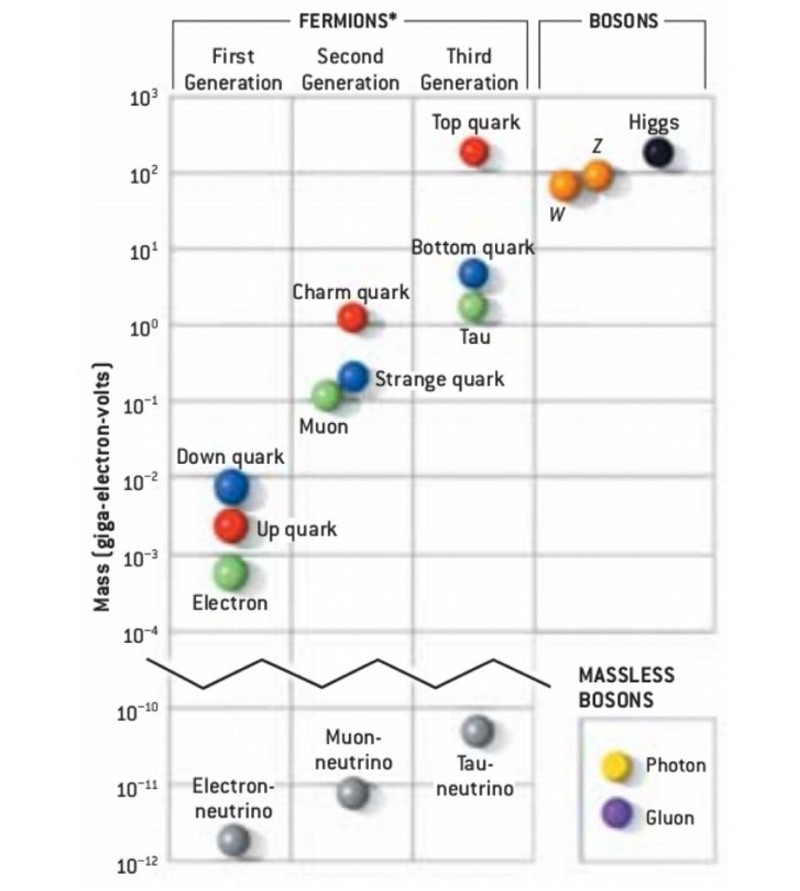
Direct constraints from experiment and observation
The two major ways that we know there are three generations — no more and no less — of fermions are as follows.
1.) The Z-boson, the neutral but very massive weak boson, has a series of different decay pathways. About 70% of the time, it decays into hadrons: particles made up of quarks and/or antiquarks. About 10% of the time, it decays into charged leptons: either the electron (1st generation), muon (2nd generation), or tau (3rd generation) flavor, all with equal probabilities. And about 20% of the time — predicted to be exactly double the frequency that it decays to a charged lepton — it decays into neutral leptons: the neutrinos, with equal probability for each of the various flavors.
These neutrino decays are invisible, since it would take about a light-year worth of lead to have a 50/50 shot of detecting your average neutrino. The fact that the fraction of Z-bosons that decays into invisible constituents (i.e., neutrinos) is exactly double the fraction that decays into the known charged leptons tells us that there are only three species of neutrinos that are below half the mass of the Z-boson, or around 45 GeV/c². If there is a fourth generation of neutrino, the lightest massive particle in each of the three known generations, it’s more than a trillion times more massive than any of the other neutrinos.
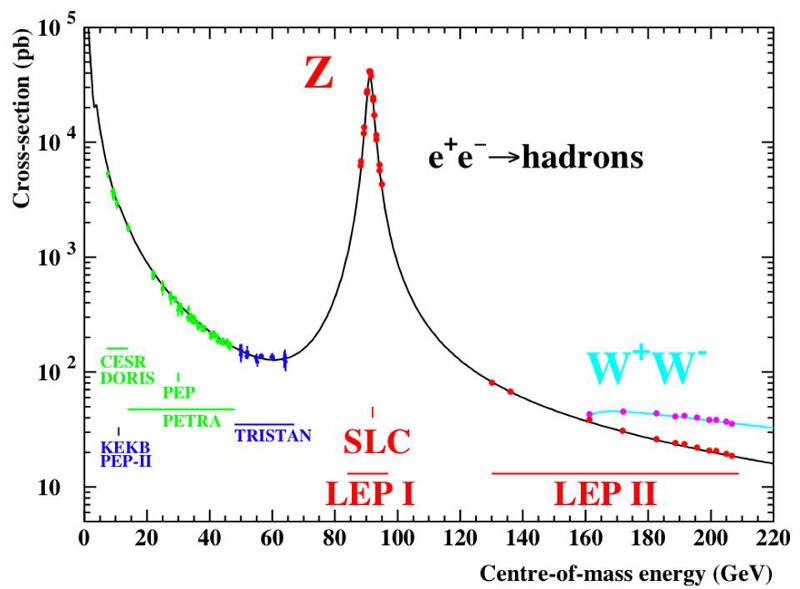
2.) The presence of neutrinos that were created in the early Universe, during the first ~second of the hot Big Bang, imprints itself onto other observable cosmic signals.
- The number of neutrino species affects the ratios of the light elements that are created during big bang nucleosynthesis, and the number of needed species is consistent with 3.
- The number of neutrino species affects the phase shift in the pattern of peaks-and-valleys that shows up in the fluctuations in the cosmic microwave background. When we compare the best observed data from the Planck satellite, we discover that there could be three or four generations of neutrinos and have that be consistent with the data, but no other number works.
- And the pattern of baryon acoustic oscillations, which is dependent on the dark matter and normal matter present in the Universe, is also sensitive to the number of neutrino species that existed in the early Universe. Once again, the “phase shift” signal that should be there not only is there, but points to the presence of three species of light neutrino.
In addition to the constraints on neutrinos, there are no additional charged leptons or quarks at masses at or below 1.2 and 1.4 TeV, respectively, from experimental constraints at the Large Hadron Collider (and the fact that probabilities must always add up to 100%).
All told, this strongly disfavors the existence of a fourth (or higher) generation of particles.
With the exception of the neutrinos, which appear to be just as stable in the “electron” species as they are in either the “muon” or “tau” species, the only stable charged particles (including neutral composite particles with charged, fundamental constituents) in the Universe are made out of first-generation quarks and leptons. The muon is the longest-lived unstable particle, and even it only has a mean lifetime of 2.2 microseconds. If you have a strange (or heavier) quark, your lifetime is measured in nanoseconds or less; if you have a tau lepton, your lifetime is measured in fractions-of-a-picosecond. There are no stable species that contain second-or-third generation quarks or charged leptons.
There are no hints in the decays of the most massive particles — the W, the Z, the Higgs or the top quark — that there are any particles in additions to the ones we know. When we look at the mass ratios of the different generations, we find that the four separate types of particles:
- the electron, muon, and tau,
- the electron neutrino, muon neutrino, and tau neutrino,
- the up, charm, and top quarks,
- and the down, strange, and bottom quarks,
all have significantly different mass ratios between the generations from one another. In addition, although quarks mix with one another and neutrinos mix across the generations, the ways in which they mix are not identical to each other. If there is a pattern or an underlying cause or reason as to why there are three generations, we haven’t uncovered it yet.

A clue from space?
One of the ideas that’s sometimes floated is really just a hint: we have three generations of fermionic particles, and we have three spatial dimension in our Universe. On the other hand, we have only one generation of bosonic particles, and one time dimension in our Universe.
Could this be a potential link; the number of spatial dimensions with the number of generations of fermions, and the number of time dimensions with the number of generations of bosons?
Maybe, but this line of thought doesn’t provide any obvious connections between the two. However, pursuing it does help us understand what similarly-minded connections aren’t present. Particles don’t have different spins or spin-modes across generations, indicating that “intrinsic angular momentum” is simple and unrelated to either generations or dimensions. There is CP-violation in the (weak) decays of heavy quarks, and that requires a minimum of three generations, but we still don’t know why there’s no CP-violation in the strong decays.
If you’re looking at “3” as though it’s a mysterious number, you might note:
- quarks have fractional charges in increments of ⅓,
- there are three colors a quark can have,
- and three possible electroweak charges (+, -, and 0),
but none of them have any known connection to either the number of spatial dimensions or the number of generations. As far as we can tell, it’s all just coincidence.
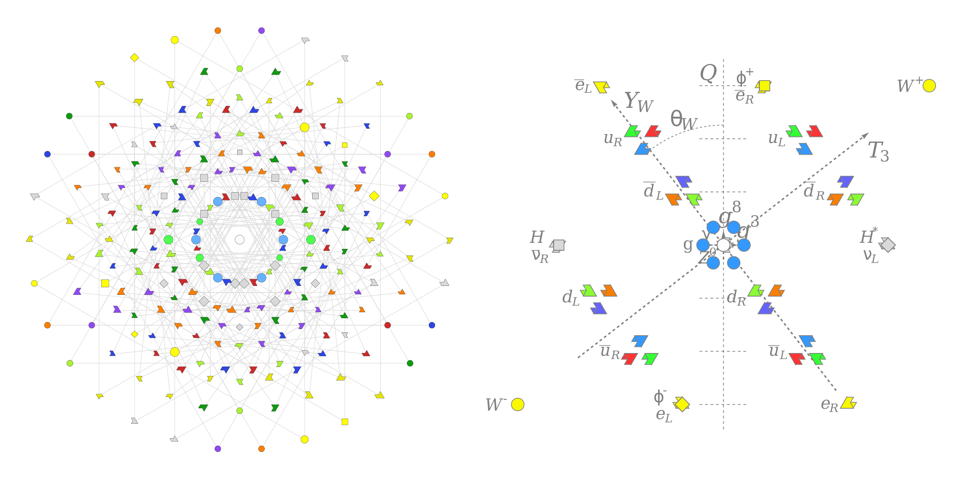
Could supersymmetry or string theory help?
Perhaps. By adding in additional symmetries and by considering larger gauge groups, it’s possible to come up with a rationale for why there would be three, and only three, generations of particles. Indeed, that’s not too far fetched. In supersymmetry, there would be more than double the number of particles than are present in the Standard Model, with an additional fermion for every boson, an additional boson for every fermion, and multiple Higgs particles as well as supersymmetric “Higgsinos” that would exist.
In string theory, we’re required to go to even greater states of symmetry, with larger gauge groups that are capable of admitting the particles of the Standard Model many times over. It is certainly possible, with such a wide set of variables to play with, to choose a way that these very large gauge groups might “break” to not only give rise to the Standard Model, but to a Standard Model that has three identical copies of its fermions, but no additional bosons.
But, again, there’s no reason that we know of that dictates why this ought to be the case. When you strike a pane of glass with a rock, it’s possible that the glass will shatter in such a way that you’ll wind up with three specific shards that are identical; that’s a plausible outcome. But unless you can predict those shards in advance, the idea doesn’t have any predictive power. Such is the case with string theory at present: it could lead to three generations of fermionic particles, but there’s no way to predict such an outcome.
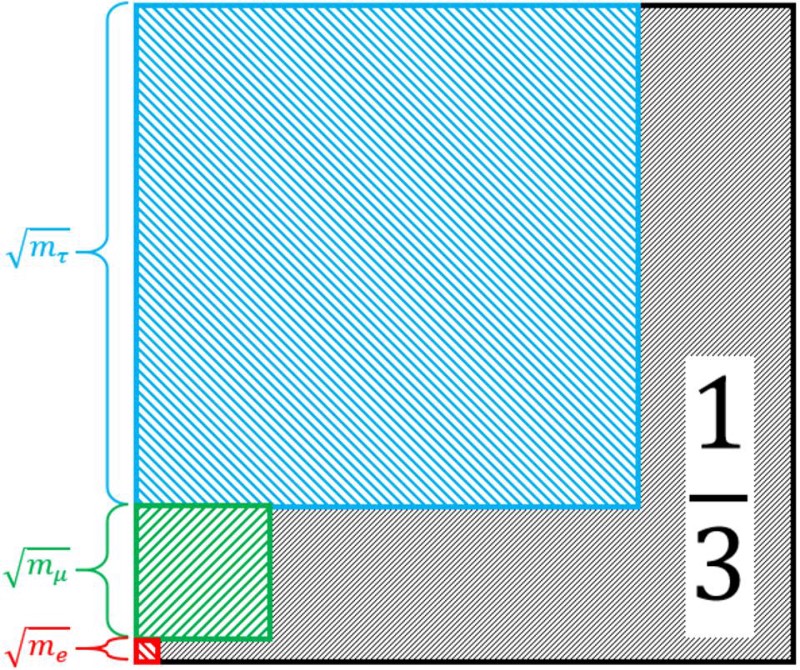
The best hint? From a virtually unknown, 40-year-old formula.
Back in 1981, physicist Yoshio Koide was looking at the then-known particles of the Standard Model and their particle properties, and took particular notice of the rest masses of the electron, muon, and tau particles. They are:
- electron: 511 keV/c²,
- muon: 105.7 MeV/c²,
- tau: 1.77 GeV/c².
Although it might appear that there’s no relationship at all between these three masses, his eponymous Koide formula indicated differently. One of the rules of quantum physics is that any particles with the same quantum numbers will mix together. With the exception of “lepton family number” (i.e., the fact that they’re in different generations), the electron, muon, and tau do have identical quantum numbers, and so they must mix.
What Koide noted was that mixing would generally lead to the following formula:
- if you add the three relevant masses together,
- and divide their sum by the square of the sum of their square roots,
- you get a simple constant out,
where that constant must lie between ⅓ and 1. When you put the numbers in, that constant just happens to be a simple fraction that splits the range perfectly: ⅔.
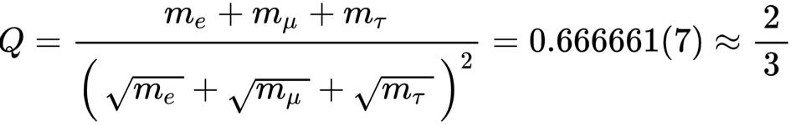
- If you apply the Koide formula to the up, down, and strange quarks, you get a fraction that’s consistent, within the measurement errors, of 5/9.
- If you apply it to the charm, bottom, and top quarks, you get a fraction consistent with 2/3.
- And if you apply it to the W, Z, and Higgs bosons, you get a fraction consistent with 1/3.
But even with all that said, there’s no underlying reason for any of this; it’s just a suggestive correlation. There may be a deep reason as to why there are three generations — no more, no less — of fermionic particles in the Standard Model, but as far as what that reason might be, we have no indicators or evidence that are any better than these tenuous connections.
The experimental data and the theoretical structure of the Standard Model, combined, allow us to conclude with confidence that the Standard Model, as we presently construct it, is now complete. There are no more Standard Model particles out there, not in additional generations nor in any other yet-undiscovered place. But there are, at the same time, certainly puzzles about the nature of the Universe that require us to go beyond the Standard Model, or we’ll never understand dark matter, dark energy, the origin of the matter-antimatter asymmetry, and many other properties that the Universe certainly possesses. Perhaps, as we take steps towards solving those mysteries, we’ll take another step closer to understanding why the Standard Model’s particle content is neither greater nor lesser than it is.