What is the Speed of Gravity?
Do changes in a gravitational field propagate instantaneously, at the speed of light, or at a different speed altogether?
“The only problem with the speed of light, is it gets here too early in the morning.” –Danny Nevrath
One of the most common questions I get asked is whether gravity is instantaneous, or whether there’s a speed limit to how fast the force of gravity can travel. This is not as simple a question as it seems on the surface.

After all, we know how fast light travels, and if the Sun were to suddenly wink out of existence, we’d still receive light from it for just over 8 minutes after it disappeared! But what about gravity, and the Earth’s orbit? Would the Earth simply fly off in a straight line, like a twirled poi ball the instant a string broke?
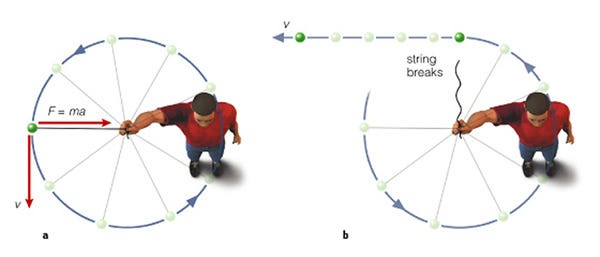
Or would it continue to move in its planetary orbit for some time, and perhaps suffer some more interesting effects? Believe it or not, this is one of the most severe differences between Newton’s old school theory of gravity and Einstein’s General Relativity. According to Newton, you have two masses separated by a distance, and that determines the force. You take one of those masses away, and the force goes away. Instantly. End of story.
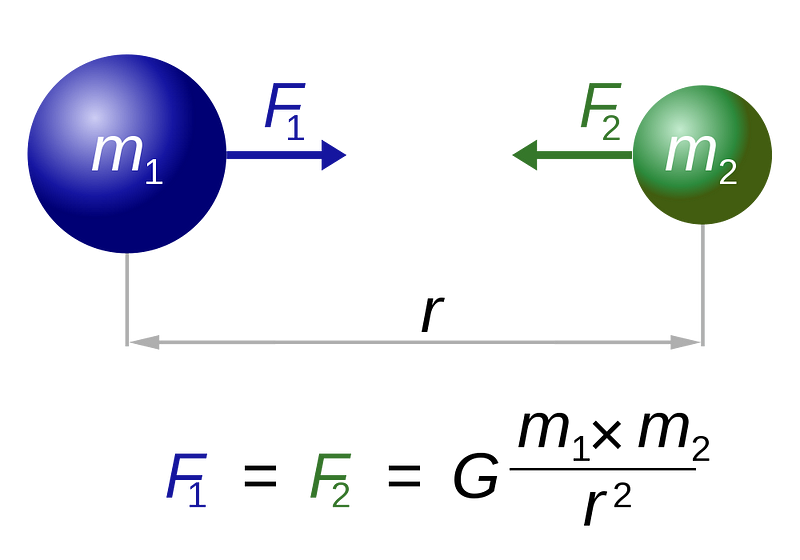
But in general relativity, things are much more intricate, and very different from the simple Newtonian picture you likely learned in high school or college.
First off, it isn’t mass, per se, that causes gravity. Rather, all forms of energy (including mass) affect the curvature of space. So for the Sun and the Earth, the incredibly large mass of the Sun dominates the curvature of space, and the Earth travels in an orbit along that curved space, just like all the other bodies in the Solar System.

If you simply removed the Sun, causing it (somehow) to wink out of existence, what would happen? In general relativity, it’s true that space would go back to being flat, but it wouldn’t do so right away at every point. In fact, just like the surface of a pond when you drop something into it, it snaps back to being flat, and the disturbances send ripples outward!

In Einstein’s theory of gravity, these ripples move at the speed of light, not instantaneously. This tells us that the distortion of spacetime due to matter and energy — as well as changes in that distortion — ought to propagate at c, and that the speed of gravity ought to be equal to the speed of light in a vacuum.
This is a really amazing idea, and leads me to ask another question. Think about it; if the Earth was stationary, it would feel the ripples in one way, but if the Earth were moving over the surface of space, wouldn’t it feel the ripples differently?

It turns out, that while Newton doesn’t care what your velocity is, Einstein does. The Sun, as it is right now, won’t have its gravity affect Earth for another 8+ minutes, and the gravity that the Earth feels right now pulling it towards the Sun is actually pulling it towards where the Sun was 8+ minutes ago! (Weird, isn’t it?)
The changes in the gravitation that Earth experiences is due to the fact that the positions and momenta of all the objects in the Universe — including the Sun — are changing over time, changing the curvature of space in our vicinity.

Want to know something that’s kind of messed up? If that was the only thing that was different from Newtonian gravity, Einstein’s theory would be wrong. The predictions that we’d get for planetary orbits, based on where objects like the Sun and the other planets were 8+ minutes ago (or whatever the light-travel time for the planet in question was) are different enough from even observations a century ago that General Relativity would have been determined to be false right away. This effect on its own demanded that, if Newton’s theory was right, the speed of gravity be at least 20 billion times faster than the speed of light!
But there is another piece to the puzzle.
The Earth, since it’s also moving, kind of “rides” over the ripples traveling through space, so that it comes down in a different spot from where it was lifted up. It looks like we have two effects going on: each object’s velocity affects how it experiences gravity, and so do the changes that occur in gravitational fields.

What’s amazing is that the changes in the gravitational field felt by a finite speed of gravity and the effects of velocity-dependent interactions cancel almost exactly! The inexactness of the cancellation is what allows us to determine, observationally, if Newton’s “infinite speed of gravity” model or Einstein’s “speed of gravity = speed of light” model matches with our Universe.
In theory, we know that the speed of gravity should be the same as the speed of light. But the Sun’s force of gravity out here, by us, is far too weak to measure this effect. In fact, it gets really hard to measure, because if something moves at a constant velocity in a constant gravitational field, there’s no observable affect at all. What we’d want, ideally, is a system that has an object moving with a changing velocity through a changing gravitational field. What would that take?
Something intense, like a neutron star orbiting another stellar-mass object extremely close together! Occasionally, we get very lucky, and a neutron star emits very regular blips of light, pulsing with incredible precision: this makes it a pulsar!
In very rare cases, we even have two neutron stars orbiting one another! If one of these neutron stars is a pulsar aimed at us, we can test whether gravity moves at the speed of light or not! Incredibly enough, we’ve discovered multiple independent binary pulsars with this exact configuration!
Not only is the gravitational source (star #1) moving, but the other object (star #2) is changing its velocity, as it changes its direction in orbit around the gravitational source! Remarkably, this effect causes the orbit to ever-so-slowly decay, which leads to time changes in the pulses!
The predictions from Einstein’s theory of gravity are incredibly sensitive to the speed of light, so much so that even from the very first binary pulsar system, PSR 1913+16 (or the Hulse-Taylor binary), we have constrained the speed of gravity to be equal to the speed of light with a measurement error of only 0.2%!
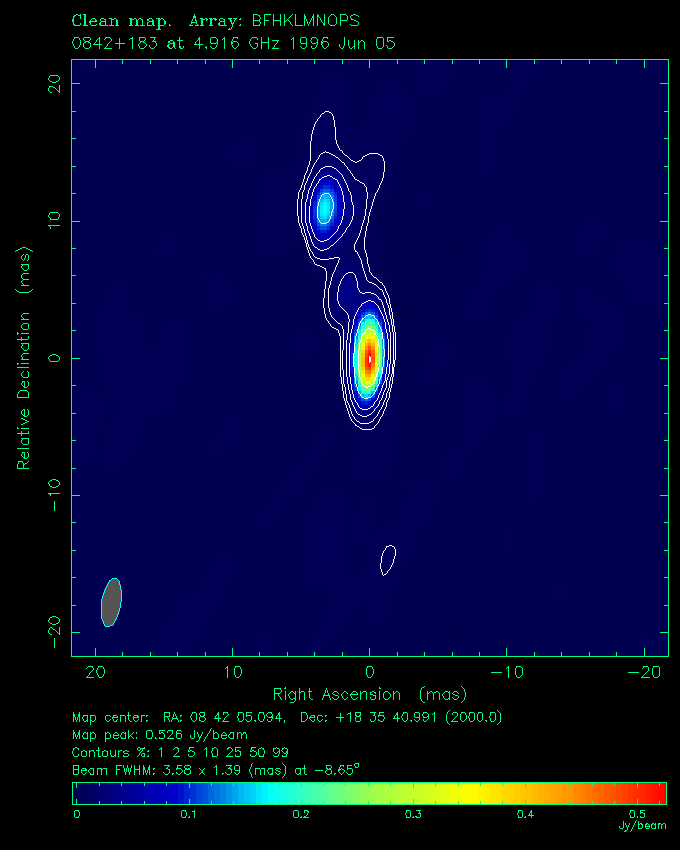
We were able to do a more direct measurement in 2002, when a chance coincidence lined up the Earth, Jupiter, and a very strong radio quasar (QSO J0842+1835) all along the same line-of-sight! As Jupiter moved between Earth and the quasar, the gravitational bending of Jupiter allowed us to measure the speed of gravity, ruling out an infinite speed and determining that the speed of gravity was between 2.55 × 10^8 and 3.81 × 10^8 meters-per-second, completely consistent with Einstein’s predictions.
But what we’d really love to be able to do is detect these gravitational waves directly.
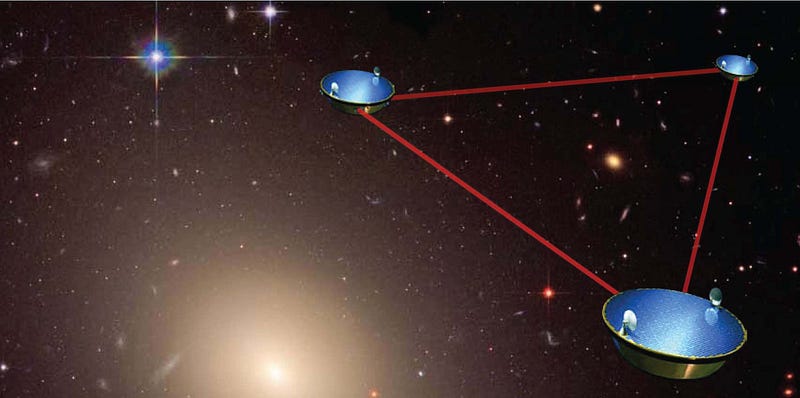
The proposed Laser Interferometer Space Antenna (LISA) would have been sensitive to exactly these types of gravitational waves, and could have measured the speed of gravity directly. If you had asked about this just a decade ago, I would have told you that LISA should be taking data by 2018. Unfortunately, NASA pulled out of the project in 2011, and it looks like this will never become a reality, not for the next 20 years unless something changes.
So until then, it’s the indirect measurements from very rare pulsar systems that give us the tightest constraints, and tell us that the speed of gravity is between 2.993 × 10^8 and 3.003 × 10^8 meters per second, which is an amazing confirmation of General Relativity and a terrible difficulty for alternative theories of gravity that don’t reduce to General Relativity! (Sorry, Newton!) And now you know not only what the speed of gravity is, but where to look to figure it out!
An earlier version of this post originally appeared on the old Starts With A Bang blog at Scienceblogs.





