No, our Universe isn’t made of pure mathematics

- We've arrived at many ideas, some of which are physically relevant to our reality, through purely mathematical ideation.
- However, mathematics alone won't paint an accurate picture of reality; we must reconcile what we "think" with what we can observe and measure.
- Playing in the sandbox is fine, but recognize it for what it actually is: mathematical playtime. If you want reality, confront the Universe itself.
At the frontiers of theoretical physics, many of the most popular ideas have one thing in common: they begin from a mathematical framework that seeks to explain more things than our currently prevailing theories do. Our current frameworks for General Relativity and Quantum Field Theory are great for what they do, but they don’t do everything. They’re fundamentally incompatible with one another and cannot sufficiently explain dark matter, dark energy, or the reason why our Universe is filled with matter and not antimatter, among other puzzles.
It’s true that mathematics enables us to quantitatively describe the Universe, it’s an incredibly useful tool when applied properly. But the Universe is a physical, not mathematical entity, and there’s a big difference between the two. Here’s why mathematics alone will always be insufficient to reach a fundamental theory of everything.
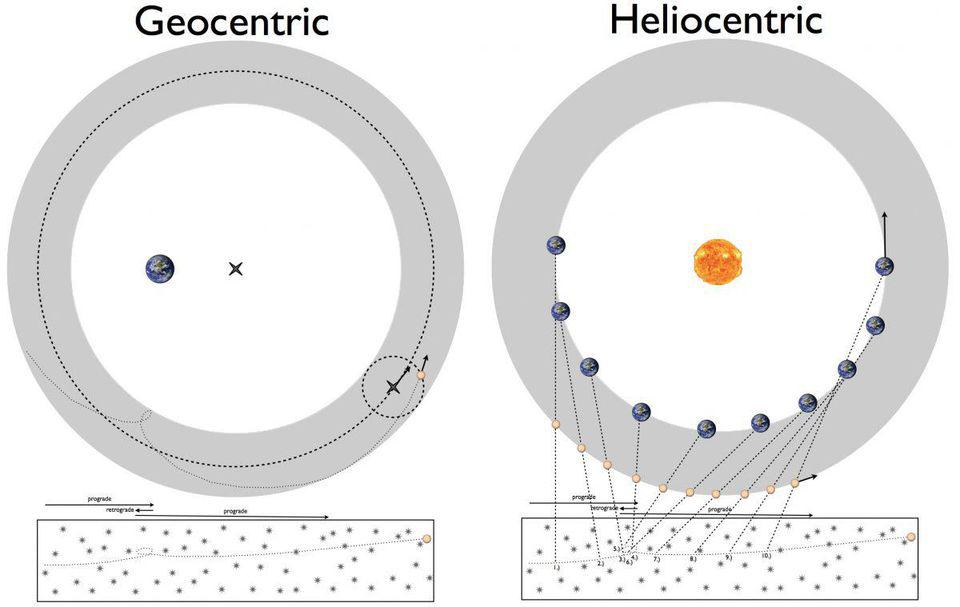
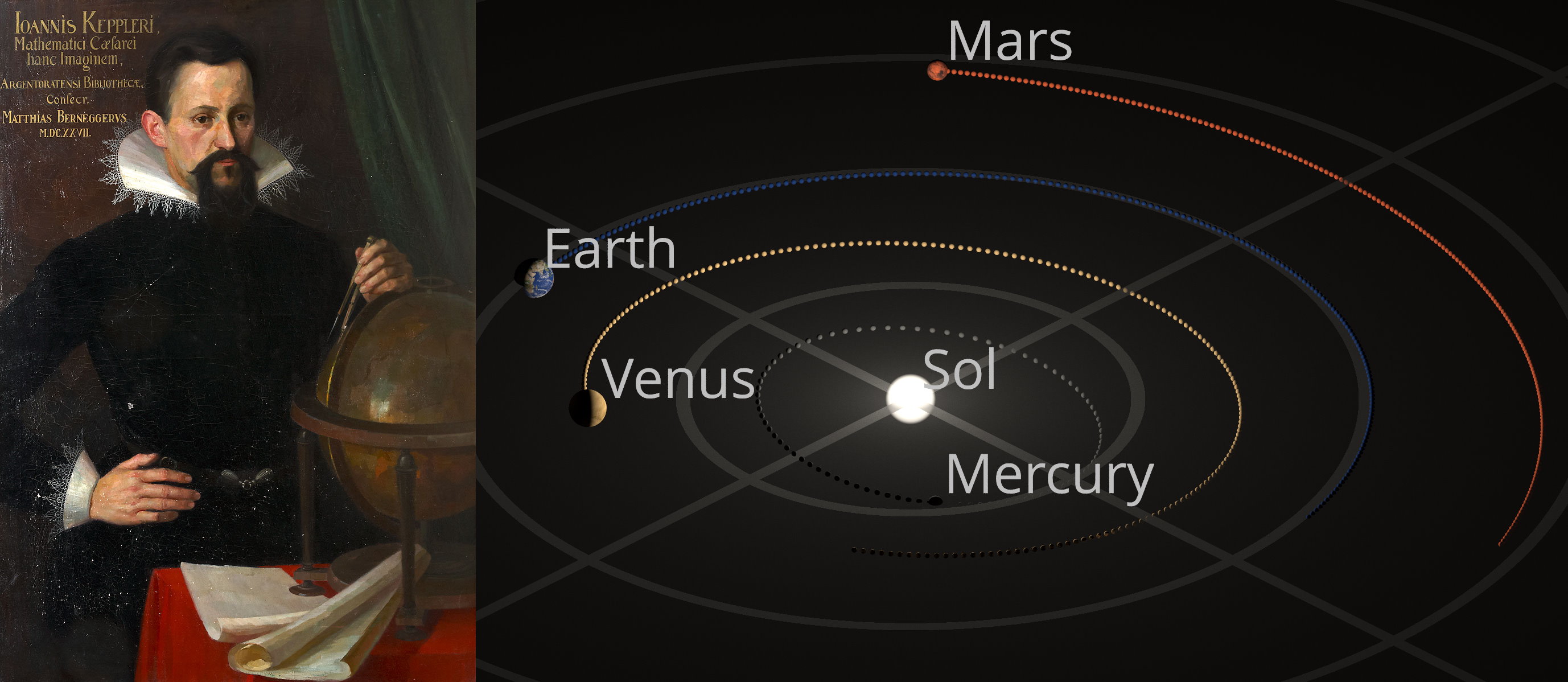
About 400 years ago, a battle was unfolding about the nature of the Universe. For millennia, astronomers had accurately described the orbits of the planets using a geocentric model, where the Earth was stationary and all the other objects orbited around it. Armed with the mathematics of geometry and precise astronomical observations — including tools like circles, equants, deferents, and epicycles — the precise mathematical description of the heavenly bodies’ orbits matched what we saw spectacularly.
The match wasn’t perfect, however, and attempts to improve upon it either led to more epicycles or, in the 16th century, Copernicus’ heliocentrism. By placing the Sun at the center, explanations of retrograde motion became simpler, but the fits to the data were worse. When Johannes Kepler came along, he had a brilliant idea that sought to solve everything.

He noticed that there were six planets total, if you included Earth but not Earth’s Moon. He also noticed that mathematically, there were only five Platonic solids: five mathematical objects whose faces are all equal-sided polygons. By drawing a sphere inside and outside each one, he could “nest” them in a way that fit the planetary orbits extremely well: better than anything Copernicus had done. It was a brilliant, beautiful mathematical model, and arguably the first attempt at constructing what we might call “an elegant Universe” today.
But observationally, it failed. It failed to even be as good as the ancient Ptolemaic model with its epicycles, equants and deferents. It was a brilliant idea, and the first attempt to argue — from pure mathematics alone — how the Universe ought to be. But it just didn’t work.
What came next was a stroke of genius that would define Kepler’s legacy.
He took his beautiful, elegant, compelling model that disagreed with observations and threw it away. Instead, he went and dove into the data to find what types of orbits would match how the planets actually moved, and came away with a set of scientific (not mathematical) conclusions.
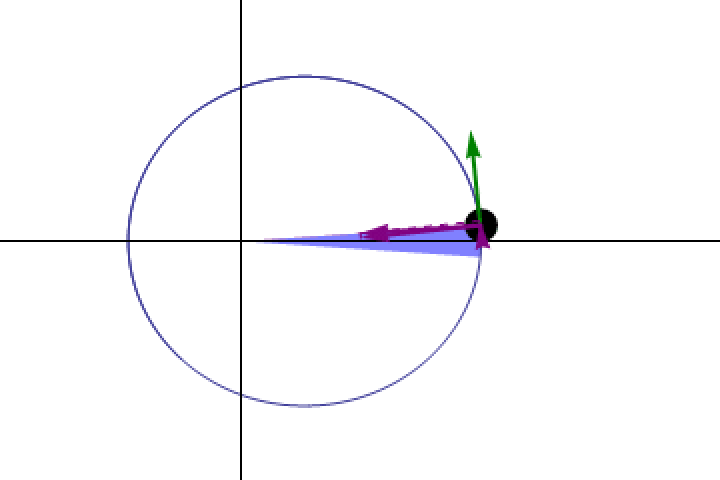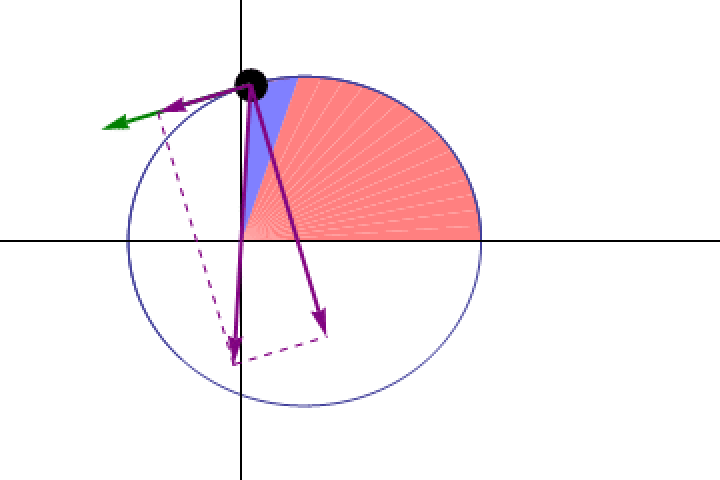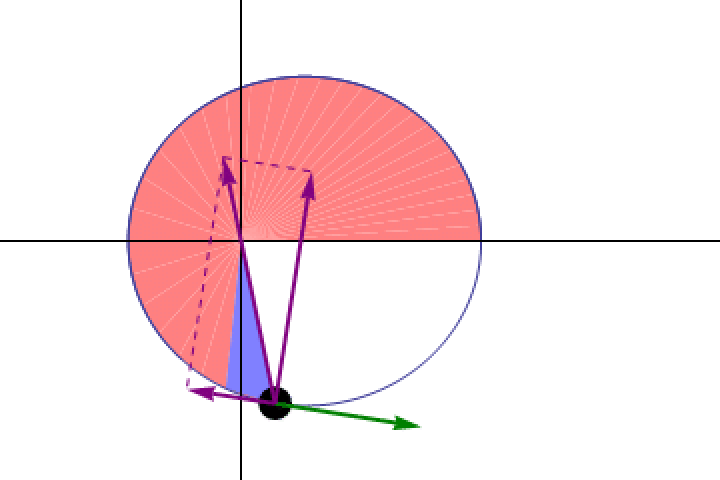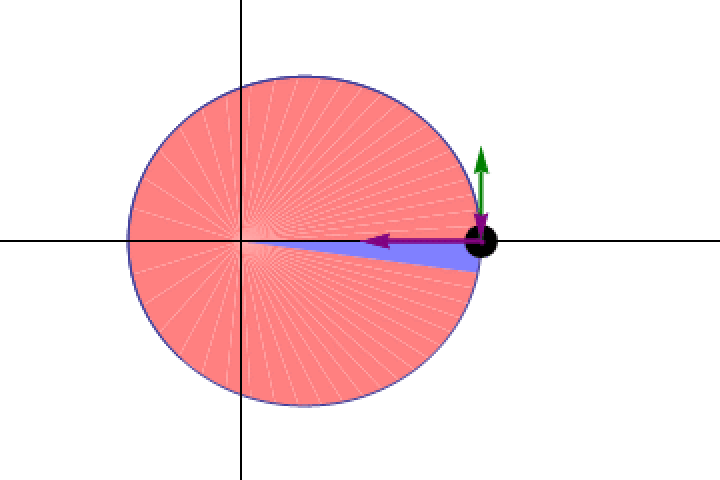
- Planets didn’t move in circles around the centrally located Sun, but rather in ellipses with the Sun at one focus, with a different set of parameters describing the ellipse of each planet.
- Planets didn’t move at a constant speed, but rather moved at a speed that varied with the planet’s distance from the Sun, in such a way that planets sweep out equal areas in equal times.
- And finally, planets exhibited orbital periods that were directly proportional to the long axis (the major axis) of each planet’s ellipse, raised to a specific power (determined to be 3/2).
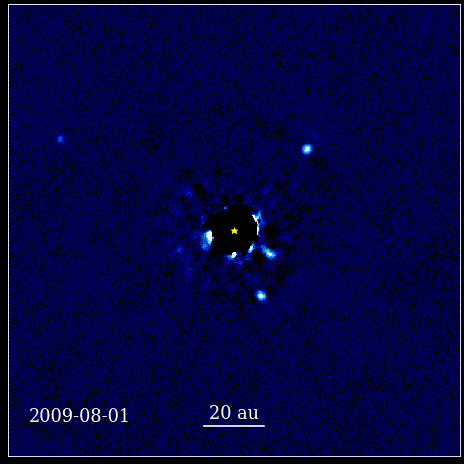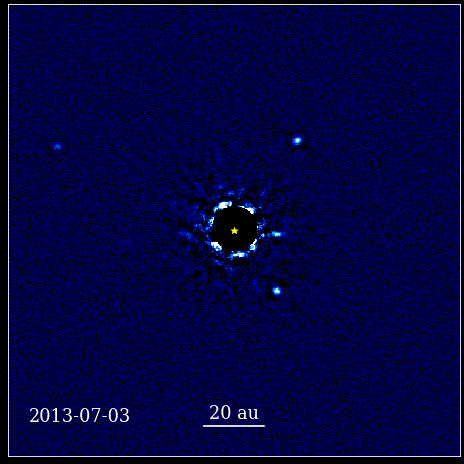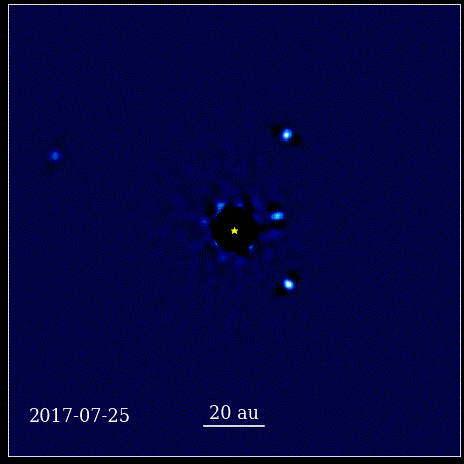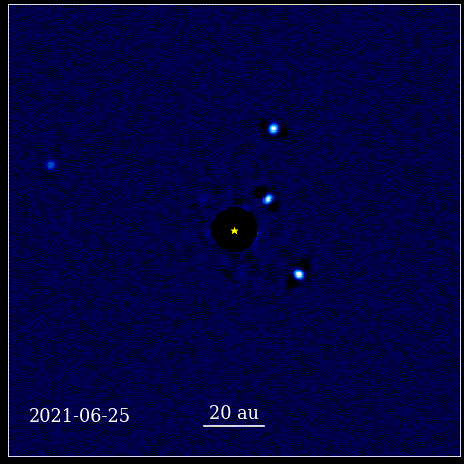
This was a revolutionary moment in the history of science. Mathematics wasn’t at the root of the physical laws governing nature; it was a tool that described how the physical laws of nature manifested themselves. The key advance that happened is that science needed to be based in observables and measurables, and that any theory needed to confront itself with those notions. Without it, progress would be impossible.
This idea came up again and again throughout history, as new mathematical inventions and discoveries empowered us with new tools to attempt to describe physical systems. But each time, it wasn’t simply that new mathematics told us how the Universe worked. Instead, new observations told us that something beyond our currently understood physics was required, and pure mathematics alone was insufficient to get us there.

By the early 1900s, it was clear that Newtonian mechanics was in trouble. It could not explain how objects moved near the speed of light, leading to Einstein’s special theory of relativity. Newton’s theory of universal gravitation was in similarly hot water, as it could not explain the motion of Mercury around the Sun. Concepts like spacetime were just being formulated, but the idea of non-Euclidean geometry (where space itself could be curved, rather than flat like a 3D grid) had been floating around for decades among mathematicians.
Unfortunately, developing a mathematical framework to describe spacetime (and gravitation) required more than pure mathematics, but the application of mathematics in a particular, tweaked way that would agree with observations of the Universe. It’s the reason why we all know the name “Albert Einstein,” but very few people know the name “David Hilbert.”

Both men had theories that linked spacetime curvature to gravity and the presence of matter and energy. Both of them had similar mathematical formalisms; today an important equation in General Relativity is known as the Einstein-Hilbert action. But Hilbert, who had come up with his own, independent theory of gravity from Einstein, pursued bigger ambitions than Einstein: his theory applied to both matter and electromagnetism as well as gravity.
And that simply didn’t agree with nature. Hilbert was constructing a mathematical theory as he thought it ought to apply to nature and could never get out successful equations that predicted the quantitative effects of gravity. Einstein did, and that’s why the field equations are known as the Einstein field equations, with no mention of Hilbert. Without a confrontation with reality, we don’t have physics at all.

This almost identical situation came up again just a few years later in the context of quantum physics. You couldn’t simply fire an electron through a double slit and know, based on all the initial conditions, where it would wind up. A new type of mathematics — one rooted in wave mechanics and a set of probabilistic outcomes — was required. Today, we use the mathematics of vector spaces and operators, and physics students hear a term that might ring a bell: Hilbert space.
The same mathematician, David Hilbert, had discovered a set of mathematical vector spaces that was enormously promising for quantum physics. Only, once again, its predictions didn’t quite make sense when confronted with physical reality. For that, some tweaks needed to be made to the math, creating what some call a rigged Hilbert space or a physical Hilbert space. (Where the “inner product” of that Hilbert space had physical constraints placed on it, but not for any mathematically motivated reason.) The mathematical rules needed to be applied with certain specific caveats, or the results of our physical Universe would never be recoverable.
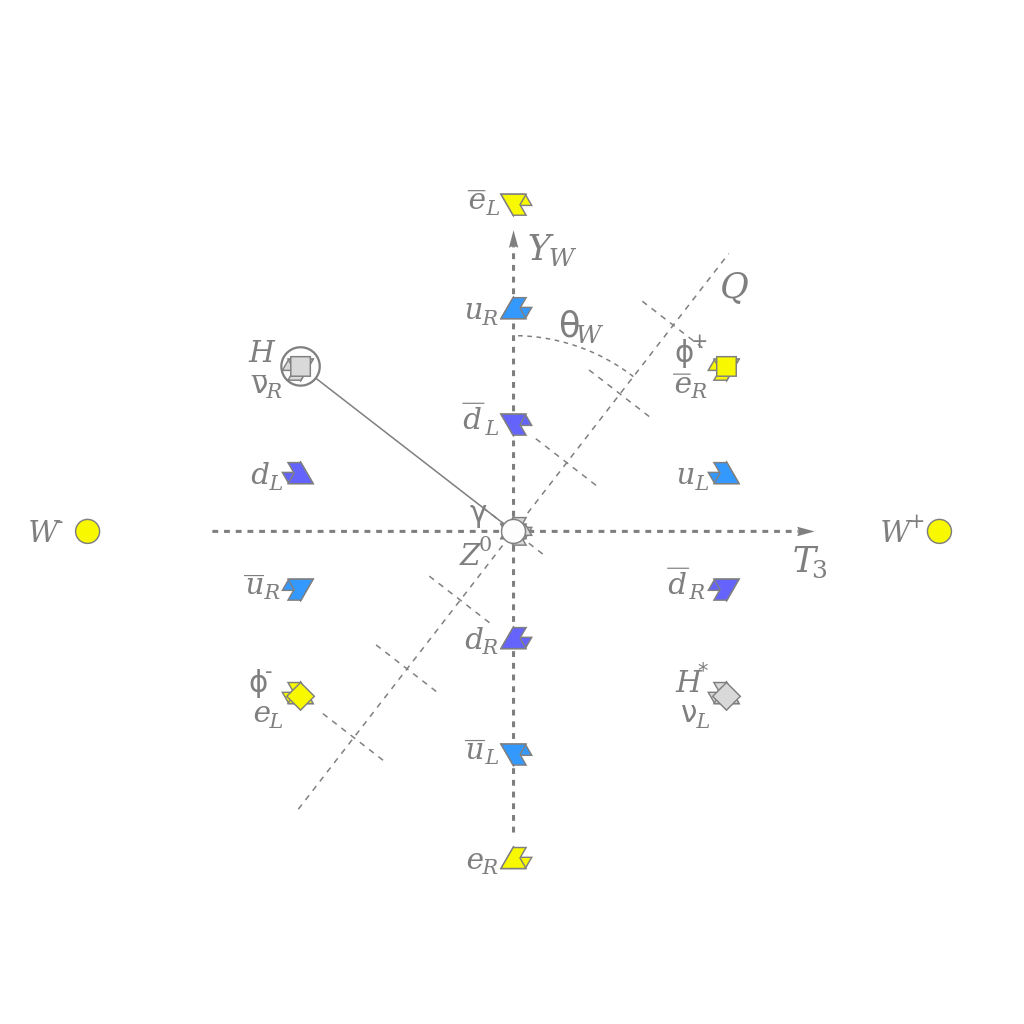
Today, it’s grown very fashionable in theoretical physics to appeal to mathematics as a potential way forward to an even more fundamental theory of reality. A number of mathematical-based approaches have been tried over the years:
- imposing additional symmetries,
- adding extra dimensions,
- adding new fields into General Relativity,
- adding new fields into quantum theory,
- using larger groups (from mathematical group theory) to extend the Standard Model,
along with many others. These mathematical explorations are interesting and potentially relevant for physics: they may hold clues as to what secrets the Universe might have in store beyond what’s presently known. But mathematics alone cannot teach us how the Universe works. We will obtain no definitive answers without confronting its predictions with the physical Universe itself.
In some ways, it’s a lesson that every physics student learns the first time they calculate the trajectory of an object thrown into the air. How far does it go? Where does it land? How long does it spend in the air? When you solve the mathematical equations — Newton’s equations of motion — that govern these objects, you don’t get “the answer.” You get two answers; that’s what the mathematics gives you.
But in reality, there’s only one object. It only follows one trajectory, landing in one location at one specific time. Which answer corresponds to reality? Mathematics won’t tell you. For that, you need to understand the particulars of the physics problem in question, as only that will tell you which answer has a physical meaning behind it. Mathematics will get you very far in this world, but it won’t get you everything. Without a confrontation with reality, you cannot hope to understand the physical Universe.