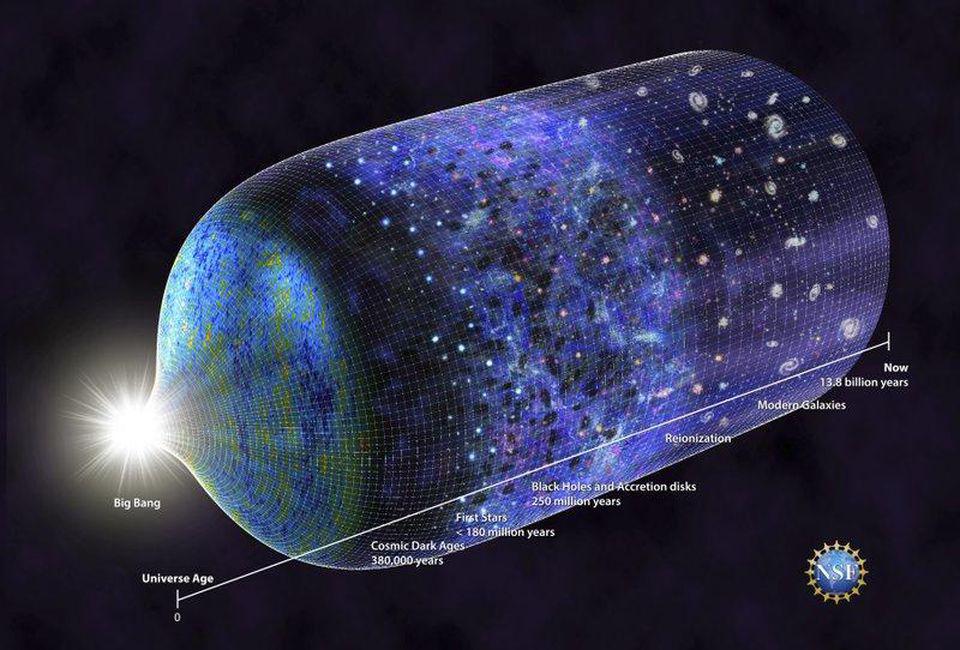
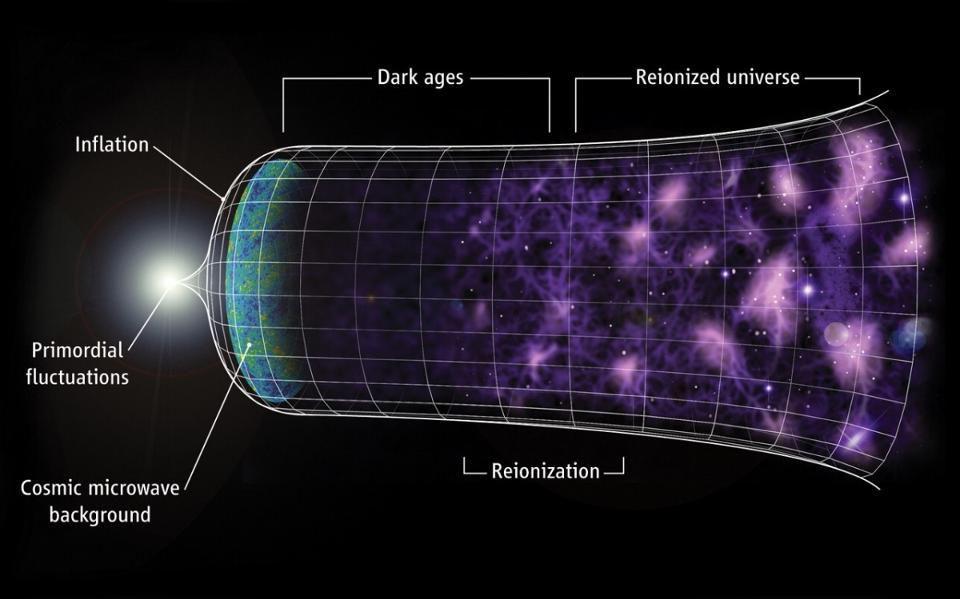
Ask Ethan: How do we know the universe is 13.8 billion years old?
- Scientists confidently state that it has been 13.8 billion years since the Big Bang, with an uncertainty of less than 1%.
- This is despite a ~9% uncertainty in the expansion rate of the universe, and knowledge of a star that’s dated at 14.5 billion years.
- It might be as little as 13.6 billion years or as much as 14.0 billion years, but it cannot be even 1 billion years older or younger than our current figure.
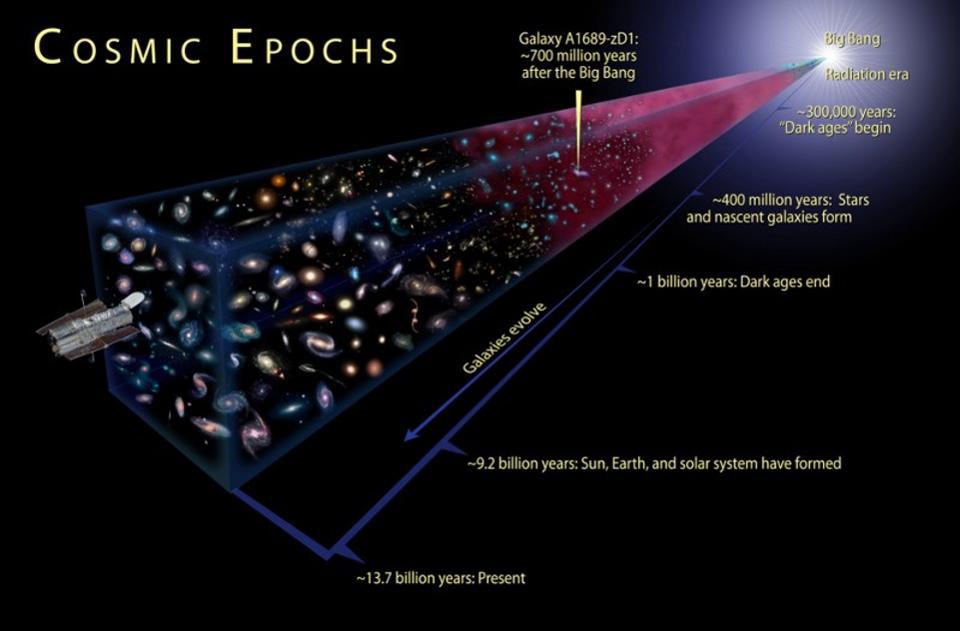
One of the most revelatory facts about the universe is that we actually know how old it is: 13.8 billion years old. If we could step back through time, we’d find that the universe as we know it was a very different place early on. The modern stars and galaxies we see today came about from a series of gravitational mergers of smaller-mass objects, which consisted of younger, more pristine stars. At the earliest stages, there were no stars or galaxies. Looking back even farther, we come to the hot Big Bang. Today, astronomers and astrophysicists who study the early universe confidently state the age of the universe with an uncertainty of no more than ~1% — a remarkable achievement that reflects the discovery of our universe’s birthday.
But how did we get there? That’s the question of Ruben Villasante, who wants to know:
“How was it determined that the big bang occurred 13.7 billion years ago?”
Now, before you say, “Oh, the question-asker says 13.7 billion instead of 13.8 billion,” know that 13.7 billion was an older estimate. (It was proposed after WMAP measured the fluctuations in the cosmic microwave background but before Planck did, so that older number is still floating around out there, both in people’s heads and in plenty of searchable webpages and diagrams.) Nevertheless, we have two ways of measuring the age of the universe, and they’re both compatible with this figure. Here’s how we know how long it’s been since the Big Bang.
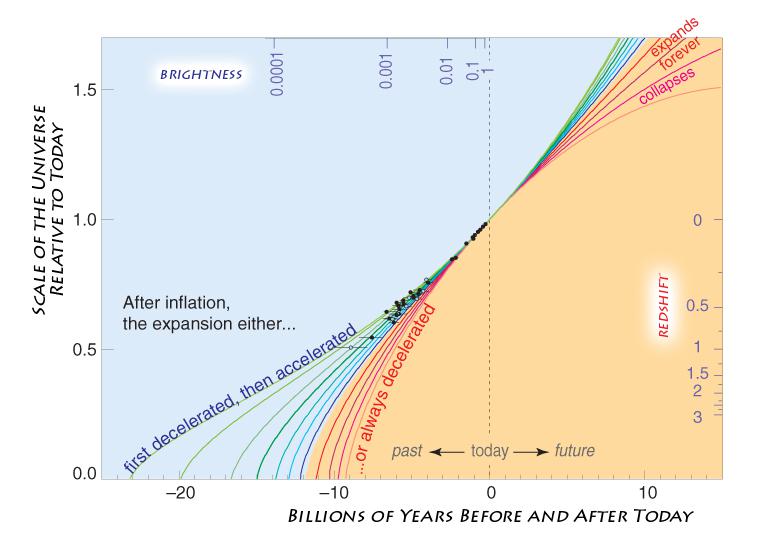
Credit: Saul Perlmutter/UC Berkeley
Method #1: tracing back the history of the universe
The first way we estimate the age of the universe is actually the most powerful. The starting point goes all the way back to the 1920s, when we first discovered the expansion of the universe. In physics, if you can uncover the equations that govern your system — i.e., the equations that tell you how your system evolves over time — then all you need to know is what that system is doing at any particular moment in time and you can evolve it as far back into either the past or future as you like. As long as both the laws of physics and the contents of your system don’t change, you’ll get it right.
In astrophysics and cosmology, the rules that govern the expanding universe come from solving general relativity for a universe that is, on average, filled with equal amounts of “stuff” everywhere and in all directions. We call this a universe that’s both homogeneous, meaning the same everywhere, and isotropic, which means the same in all directions. The equations you get are known as the Friedmann equations (after Alexander Friedmann, who first derived them), which have been around for a full 99 years now: since 1922.
These equations tell you that a universe filled with “stuff” must either expand or contract. The way the expansion (or contraction) rate changes with time is only dependent on two things:
- how fast that rate is at any one point, such as today
- what, exactly, your universe is filled with at that particular point
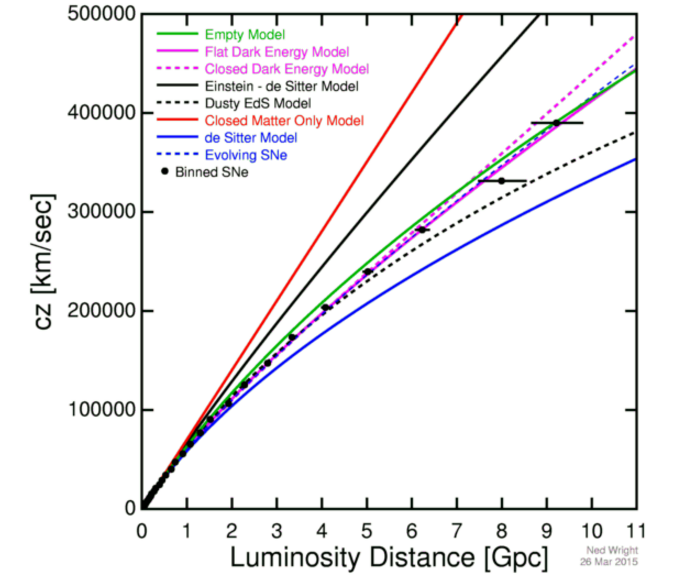
Way back in the early days of cosmology, people used to joke that “cosmology is the search for two numbers,” implying that if we could measure the expansion rate today (what we know as the Hubble parameter) and how the expansion rate changes with time (what we called the deceleration parameter, which is a horrible misnomer because it’s negative; the universe is accelerating and not decelerating), then we’d be able to determine precisely what’s in the universe.
In other words, we could know how much of it was normal matter, how much was dark matter, how much was radiation, how much was neutrinos, how much was dark energy, etc. This is a very nice approach, because they’re simply reflective of the two sides of the equation: the expansion of the universe and how it changes are on one side, while the matter-and-energy density of everything is on the other side. In principle, measuring one side of the equation will tell you the other.
You can then take what you know and extrapolate it back in time, to when the universe was in the very hot, dense, and small-volume state that corresponds to the earliest moments of the hot Big Bang. The amount of time that it takes you to wind the clock back — from now until then — tells you the age of the universe.
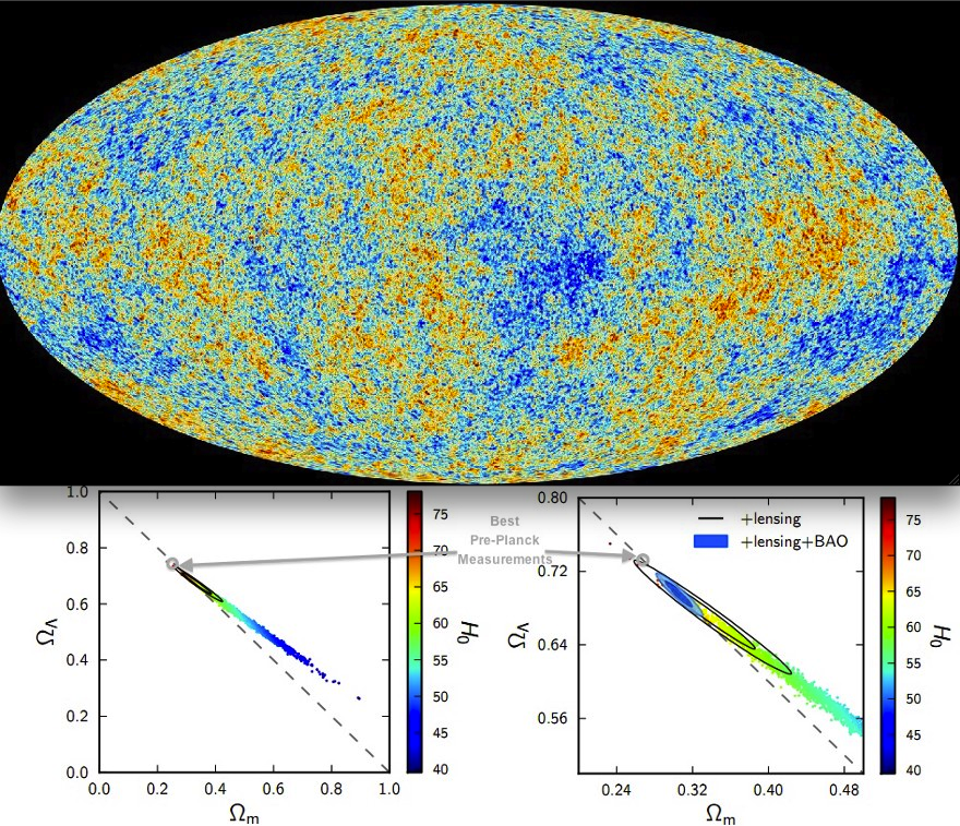
Credit: Planck Collaboration; Annotations: E. Siegel
In practice, though, we use multiple lines of evidence to all complement one another. By bringing multiple lines of evidence together, we can put together a consistent picture that folds all of these measurements together. Some of these are particularly important.
- The large-scale structure of the universe tells us the total amount of matter that’s present, as well as the normal matter-to-dark matter ratio.
- The fluctuations in the cosmic microwave background relate how quickly the universe is expanding to a variety of components in the universe, including the total energy density.
- Direct measurements of individual objects, like type Ia supernovae, at a wide variety of distances and redshifts can teach us what the expansion rate today is, and can help measure how the expansion rate has changed with time.
What we wind up with is a picture where the universe appears to be expanding at a rate of ~67 km/s/Mpc today, made of 68% dark energy, 27% dark matter, 4.9% normal matter, about 0.1% neutrinos, and less than 0.01% of everything else, such as radiation, black holes, spatial curvature, and any exotic form of energy not accounted for here.
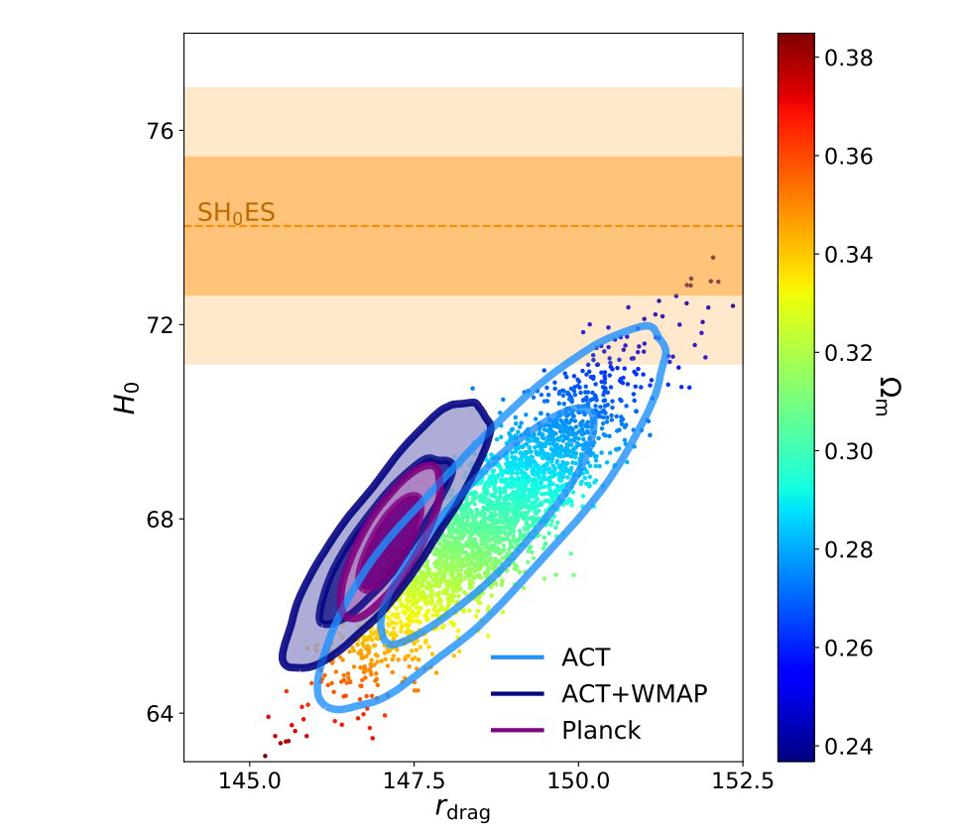
Credit: ACT Collaboration DR4
Put those pieces together — the rate of expansion today and the various contents of the universe — and you get an answer for the age of the universe: 13.8 billion years. (WMAP gave a slightly higher rate of expansion and a universe with slightly more dark energy and slightly less dark matter, which is how they obtained their earlier, somewhat less-precise value of 13.7 billion.)
It might surprise you to learn, however, that these parameters are all interrelated. For example, we might have the expansion rate wrong; it might be more like ~73 km/s/Mpc, as favored by groups who use late-time, distance ladder measurements (like supernovae) as opposed to the ~67 km/s/Mpc obtained by early-time, relic signal methods (like the cosmic microwave background and baryon acoustic oscillations). That would change the expansion rate, today, by about 9% from the preferred value.
But that wouldn’t change the age of the universe by up to 9%; in order to fit the other constraints, you’d have to alter the contents of your universe accordingly. A more rapidly expanding universe today requires more dark energy and less overall matter, while a much more slowly expanding universe would require a large amount of spatial curvature, which isn’t observed.
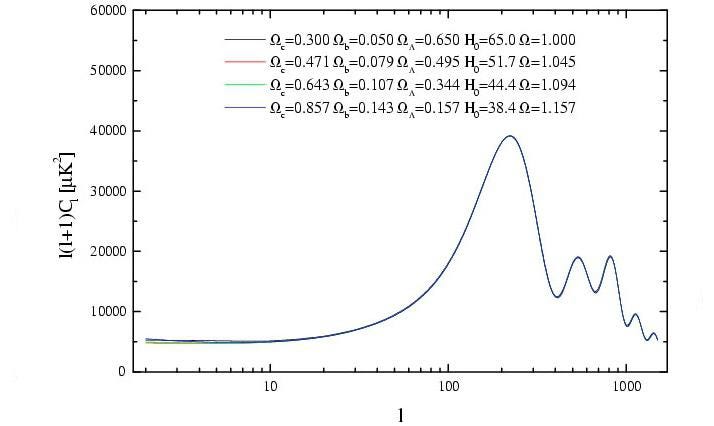
Credit: A. Melchiorri & L.M. Griffiths, 2001, NewAR
Although we’re still trying to pin down these various parameters through all our combined methods, their mutual relationships ensure that if one parameter is different, then a series of others must change as well in order to remain consistent with the full suite of data. Although a faster-expanding universe is allowed, it requires more dark energy and less overall matter, which means the universe, overall, would be only slightly younger. Similarly, the universe could expand more slowly, but would require even less dark energy, greater amounts of matter, and (for some models) a nonnegligible amount of spatial curvature.
It’s possible that the universe might be as young, if you push to the edge of our uncertainties, as 13.6 billion years. But there isn’t a way to get a younger universe that doesn’t conflict with the data too severely: beyond the limits of our error bars. Similarly, 13.8 billion isn’t the oldest the universe could possibly be; perhaps 13.9 or even 14.0 billion years is still within the realm of possibility, but any older would push the limits of what the cosmic microwave background would allow. Unless we’ve made an incorrect assumption somewhere — such as the contents of the universe changed dramatically and abruptly at some point in the distant past — there’s really only a ~1% uncertainty on this 13.8 billion year value for “how long ago the Big Bang happened.”
Fortunately, we aren’t reliant on cosmic arguments alone, as there’s another way to, if not quite measure, at least constrain the age of the universe.

Credit: ESA and NASA; Acknowledgment: E. Olszewski (University of Arizona)
Method #2: measuring the ages of the oldest stars
Here’s a statement that you’ll probably agree with: “if the universe is 13.8 billion years old, then we’d better not find any stars within it that are older than 13.8 billion years.”
The problem with this statement is that it’s very, very difficult to pin down the age of any one star in the universe. Sure, we know all sorts of things about stars: what their properties are when their cores first ignite nuclear fusion, how their life cycles depend on the ratio of elements they were born with, how long they live dependent on their mass, and how they evolve as they burn through their nuclear fuel. If we can measure a star precisely enough — which we can do for most stars within a few thousands light-years in the Milky Way — then we can trace back the star’s life cycle to the moment it was born.
That’s true — but if, and only if, that star hasn’t undergone a major interaction or merger with another massive object over its lifetime. Stars and stellar corpses can do some pretty mean things to one another. They can strip material away, making a star look more-or-less evolved than it actually is. Multiple stars can merge together, making the new star appear younger than it actually is. And stellar interactions, including interactions with the interstellar medium, can change the ratio of elements we observe within them from what was present during most of their lives.

Credit: Digitized Sky Survey, STScI/AURA, Palomar/Caltech and UKSTU/AAO
When we were talking about the entire universe, we needed to specify that this approach was only valid in the absence of major, abrupt changes that occurred in the universe’s past. Well, similarly, for stars, we have to keep in mind that we’re only getting a snapshot of how that star is behaving over the timescale we’ve been observing it: years, decades, or centuries at most. But stars typically live for billions of years, meaning that we’re only viewing them for a cosmic blink-of-an-eye.
As such, we should never put too much stock in the measurement of a single star; we have to be aware that any such measurement comes along with a large uncertainty. The so-called Methuselah star, for example, is highly unusual in a lot of ways. It’s estimated to be approximately 14.5 billion years old: some 700 million years older than the age of the universe. But that estimate comes along with an uncertainty of almost 1 billion years, meaning that it could very well be an old, but not a too old star for our present estimates.
Instead, if we want to make more accurate measurements, we need to look at the oldest collections of stars we can find: globular clusters.

Credit: Hubble Legacy Archive (NASA/ESA/STScI)
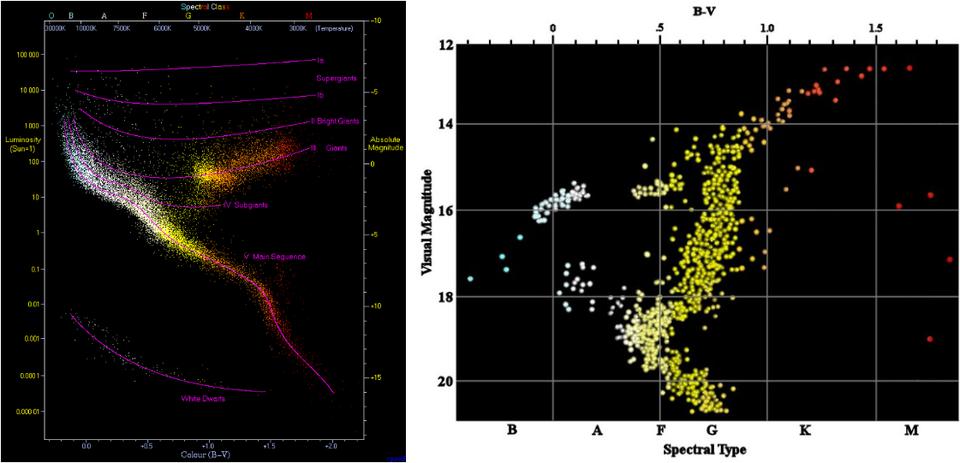
Globular clusters exist in every large galaxy; some contains hundreds (like our Milky Way), others, like M87, can contain more than 10,000. Each globular cluster is a collection of many stars, ranging from a few tens of thousands up to many millions, and each star within it will have a color and a luminosity: both easily measurable properties. When we plot the color and magnitude of each star within a globular cluster together, we get a particularly shaped curve that snakes from the lower-right (red color and low luminosity) to the upper-left (blue color and high luminosity).
Now, here’s the key thing that makes these curves so valuable: as the cluster ages, the more massive, bluer, more luminous stars evolve off of this curve, as they’ve burned through their core’s nuclear fuel. The more the cluster ages, the more “empty” the blue, high-luminosity part of this curve becomes.
When we observe globular clusters, we find they have a wide variety of ages, but only up to a maximum value: 12-something to 13-something billion years. Many globular clusters fall into this age range, but here’s the important part: none are older.
Credit: Richard Powell (L), R.J. Hall (R)
From both individual stars and stellar populations to the overall properties of our expanding universe, we can derive a very consistent age estimate for our universe: 13.8 billion years. If we tried to make the universe even one billion years older or younger, we’d run into conflicts on both accounts. A younger universe can’t explain the oldest globular clusters; an older universe can’t explain why there aren’t globular clusters that are even older. Meanwhile, a significantly younger or older universe can’t accommodate the fluctuations we see in the cosmic microwave background. Put simply, there’s too little wiggle room.
It’s very tempting, if you’re a scientist, to try and poke holes in any and every aspect of our current understanding. This helps us ensure our present framework for making sense of the universe is robust, and also helps us explore alternatives and their limitations. We can try to construct a substantially older or younger universe, but both our cosmic signals and measurements of stellar populations indicate that a small amount of wiggle room — perhaps at the ~1% level — is all we can accommodate. The universe as we know it began 13.8 billion years ago with the hot Big Bang, and anything younger than 13.6 billion or older than 14.0 billion years, unless some wild alternative scenario (that we have no evidence for) comes into play at some point, is already ruled out.
Send in your Ask Ethan questions to startswithabang at gmail dot com!