Time crystals are real, but that doesn’t mean time is crystallized

If you heard about time crystals, be aware that they do exist. But learn what they mean.
“Every particular in nature, a leaf, a drop, a crystal, a moment of time is related to the whole, and partakes of the perfection of the whole.”
–Ralph Waldo Emerson
In 2012, Nobel Laureate Frank Wilczek proposed a new state of matter that had never been theorized before: a time crystal. The “crystal” part of that name is something our intuition and experience matches up with: a repeating, rigid lattice of atoms or molecules bound together into a solid, ordered structure. But the “time” part doesn’t mean that it’s time itself that’s been crystallized. Instead, it means that a fundamental symmetry of nature — time translation symmetry — isn’t obeyed within the crystal.
Initially, time crystals were regarded as merely a theoretical curiosity, and assumed to be an experimental impossibility. Theorems were published, proving their impossibility. But loopholes in the theorems were discovered, and ideas for creating them emerged. Over the past year, for the first time, these crystals have been created in the lab by two independent groups. The incredible discovery potentially paves the way for Wilczek to become the first theorist to win two Nobel Prizes in physics.
Wilczek’s first Nobel Prize came for the discovery of asymptotic freedom: that inside a proton, the closer quarks get to each other, the smaller the attractive force holding them together gets. This is contrary to all the other known forces, where forces increase at shorter distances. Wilczek’s work was pioneering in the understanding of the Strong Nuclear Force, in the development of Quantum Chromodynamics and in the completion of the Standard Model.
Wilczek’s primary advances came in the field of theoretical particle physics and quantum field theories. But quantum field theories also apply to condensed matter systems: systems with large numbers of particles that exhibit intricate quantum behaviors. There are degrees of freedom to any system — ways that it can change or adjust — both classical or quantum. The idea of a time crystal, in both classical and quantum versions, is that it should repeat its configuration, so long as it stays in its ground state, periodically in time. Just as a normal crystal repeats its configured molecular/atomic pattern periodically in space, a time crystal should have this same property except for time.
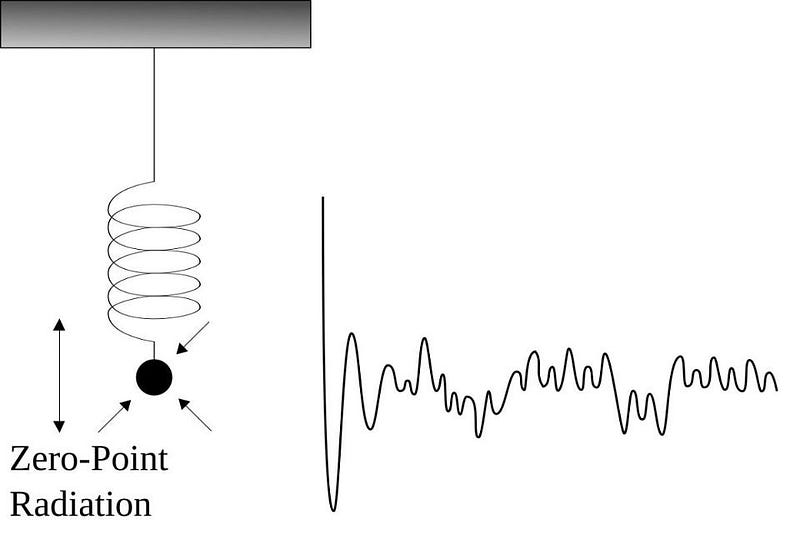
This would seem to be a problem, though, for physics. If you’re moving from one state to another to another, and then back to your initial state, that would appear to indicate some type of perpetual motion, which shouldn’t be possible due to the conservation of energy. In fact, there’s a theorem forbidding this behavior for classical systems, and it’s been thought to be strictly forbidden for quantum ones as well.
As it turned out, though, Norman Yao and his team, in 2016, came up with a scheme where the creation of these time crystals actually seemed possible. Instead of a closed, constant system, he proposed taking the system out-of-equilibrium. By driving the system externally — making it an “open” instead of a “closed” system — he realized that, at least in theory, there were some physical conditions under which this time-translation-symmetry could be broken.
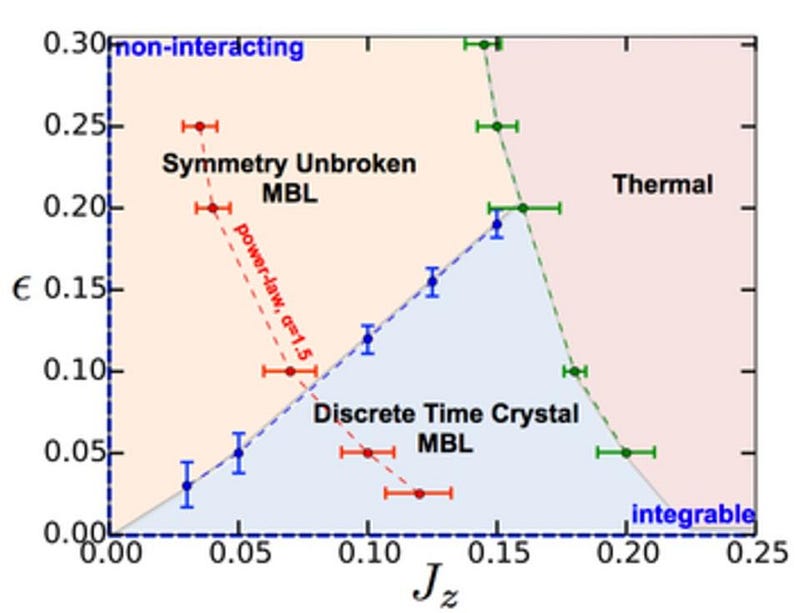
The two things that needed to be varied in Yao’s model were the Ising interaction strength, which represents the dipole moments of the atomic spins (x-axis, above), and spin-echo pulse imperfections, which represents the external driving of the crystal (y-axis, above). For certain classes of combinations, this should yield a time crystal. Yao’s work was first shared with the world in August of 2016, and it was since put to the test by two groups: Mikhail Lukin’s at Harvard and Christopher Monroe’s at University of Maryland. Both groups, it appears, have been able to successfully create these time crystals under laboratory conditions.
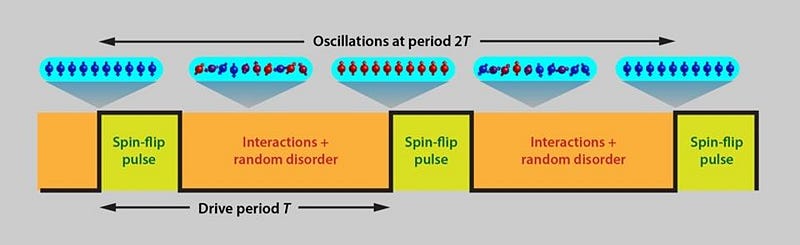
What does “driving” a system mean? It means that you send a “spin-flip pulse” of a particular strength through the system. And what you get is a periodic response that’s directly proportional to the time at which you’re pulsing the system. This isn’t an “of course” moment, either, but rather quite a surprise, as physicist Douglas Natelson states:
Achieving some kind of steady-state with spontaneous time periodicity and a lack of runaway heating due to many-body interacting physics is pretty restrictive.
Interestingly, you can make the driving imperfect in a number of ways: by slightly altering the magnitude of the pulse, by varying the frequency of the pulsation, etc., and still the period of the time crystal oscillations to-and-from the initial state remains rigidly locked.
It’s also fascinating that the two groups took vastly different approaches to implementing Yao’s model, and both succeeded. Monroe’s group took a one-dimensional line of yttrium ions coupled by their electrostatic interactions, and found that the system exhibited time crystal oscillations with a frequency of twice the pulse period, even when the driving was imperfect. Lukin’s, on the other hand, took a million spin-impurities in a diamond crystal and pulsed them with microwave radiation, which flipped their spins, and found time crystal oscillations at three times the pulse period.
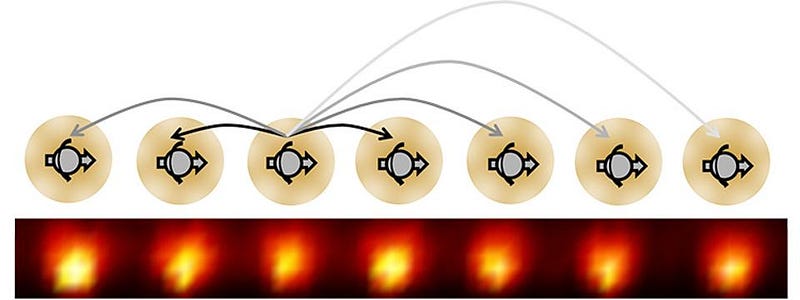
Still, time crystals as Wilczek originally envisioned them — in systems in thermal equilibrium — really do appear to be impossible. You have to have an open system, and the system needs to be driven at a periodic frequency with imperfections that aren’t too large. Over-drive it, and the crystal will “melt,” losing the properties that made it so interesting in a periodic fashion. We still haven’t crystallized time, and likely never will. But the ability to make a system, that when all you do is pulse it in a particular way, returns, periodically, to a uniform state over and over again, is truly remarkable.
The existence of time crystals may eventually be applied to quantum computers, vastly increasing their power and potentially allowing them to be constructed at much higher temperatures than today. Someday in the not-too-distant future, there may be a Nobel Prize split between Wilczek, Yao, Lukin and Monroe. The only big debate, if it happens? Who gets left out. The Nobel Prize is limited to three people, maximum, and so that’s a debate that goes well beyond anything that the science can decide.
Reference: “Discrete Time Crystals: Rigidity, Criticality, and Realizations,” N. Y. Yao, A. C. Potter, I.-D. Potirniche, and A. Vishwanath, Phys. Rev. Lett. 118, 030401.
This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!