This One Thought Experiment Shows Why Special Relativity Isn’t The Full Story

As soon as you start thinking about energy and gravity, you’ll realize the need to go beyond it.

When it comes to a science like physics, theoretical expectations must always be confronted with experimental results if we ever hope to comprehend the Universe around us. From the theoretical side, we can envision any configuration of particles and forces that we like, and then — when our technological capabilities allow — we can put those expectations to the test, and find out just how good our theory is.

Of course, sometimes we get ahead of ourselves, and envision experiments that we have no foreseeable way of carrying out. This isn’t a flaw in our theorizing, however, but rather a feature. In our own imaginations, even without the experimental apparatus to make it a reality, we can conduct our own thought-experiments: what Einstein called a gedankenexperiment in his native German. If we conceive of it correctly, we can show with just a thought that special relativity, the first of Einstein’s greatest discoveries, cannot be fully correct.

Every theory, idea, or hypothesis will always have a limited range of validity. Newton’s laws of motion worked great to describe the motion of ball falling on Earth, of the Moon orbiting in space, of the planets and comets revolving around the Sun, and a great deal more. But despite centuries of unbridled success, these laws couldn’t describe everything.

When we started observing the orbit of Mercury in great enough detail, we found that Newton’s law of gravitation didn’t perfectly describe how Mercury’s orbit behaved. A tiny, extra precession was consistently observed over and above what was predicted, necessitating an explanation. Additionally, when speeds approached the speed of light, Newton’s equations failed to predict the behavior of particles. Under the right conditions, Newton’s formulation of the Universe would need to be revised.

Einstein’s special relativity was the first earnest attempt to take physics beyond the shackles of Newtonian mechanics. Instead of viewing space and time as absolutes, as Newton did, Einstein tied them inextricably together. The closer to the speed of light you moved, the more distances would appear to contract along your direction of motion, and the slower external clocks would appear to run.

Similarly, a stationary observer who perceived you in motion would see your length contract and your time dilate in an amount that was directly related to the relative speed at which you moved. However, even though the rules for calculating kinetic energy (or the energy of motion) of an object are different in special relativity from how they are in Newtonian mechanics, energy is still conserved, and can be converted from one form into another. This fact is vitally important, and leads to our great thought experiment which shows that special relativity cannot be the full story.

Another of Einstein’s great breakthroughs is the notion of mass-energy equivalence. Commonly expressed as E = mc², it means that the amount of energy inherent to any massive particle (or antiparticle) that exists is equal to that particle’s mass, multiplied by a factor of the speed of light squared. It also can be written, as Einstein originally expressed it, as m = E/c², which details the mass (m) you’ll achieve by creating a particle out of a specific amount (E) of energy.

If you take a particle-antiparticle combination, where both particles and antiparticles each have a specific mass, you can collide them together from rest and watch them annihilate. When they do, one common outcome is that they’ll produce two photons: massless particles that will go off at 180° angles to one another with a specific amount of energy. Each one will possess exactly the amount of energy, E, that you’d get by converting the mass (m) of both the particle and antiparticle into pure energy from Einstein’s most famous equation.

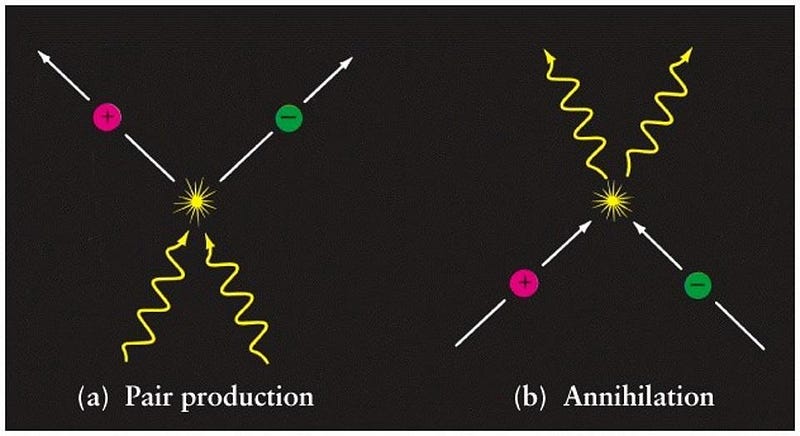
So far, nothing is controversial. We can take particle-antiparticle pairs at rest and annihilate them, producing two photons of a specific, well-defined energy. Also, we have notions of kinetic and potential energy that remain with us from Newton’s old formulation, and special relativity, which tells us that the speed of light in a vacuum is the ultimate cosmic speed limit, and that massive particles must always move slower than that speed.

But we can create an interesting thought experiment just from these ingredients. In fact, we can prove, from this thought experiment, that a phenomenon that exists exclusively in General Relativity — that of gravitational redshifts and blueshifts — must be physically real. If someone had thought this way back in 1905, perhaps they even would have beaten Einstein to the formulation of the 20th century’s most revolutionary idea.

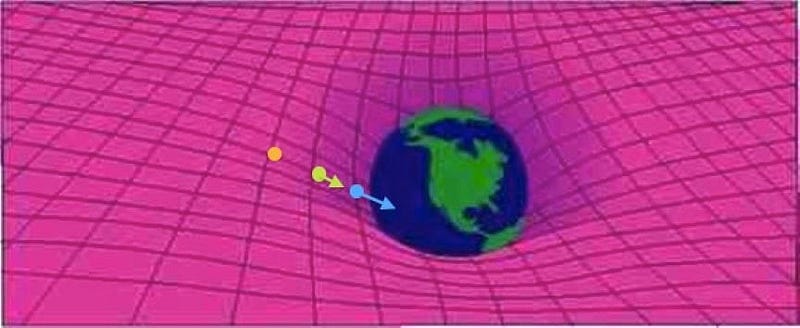
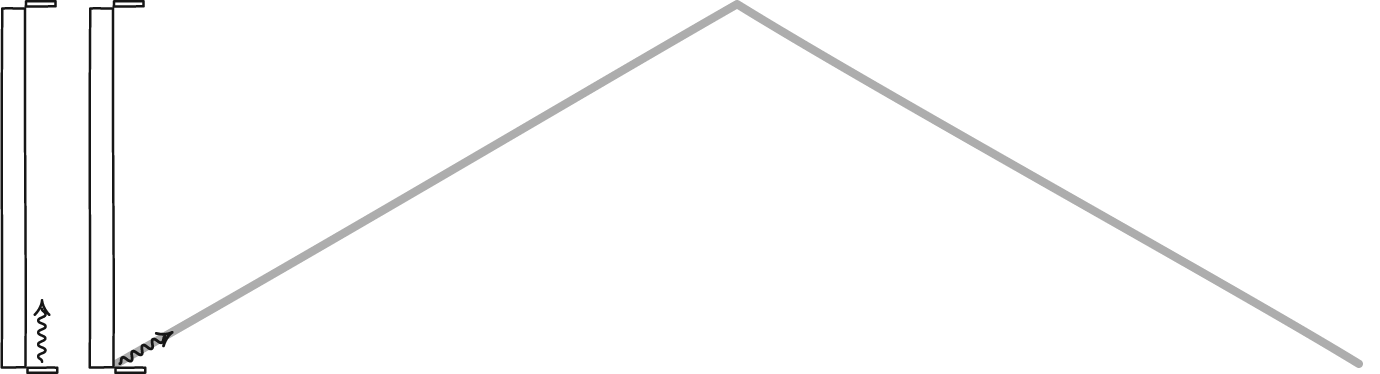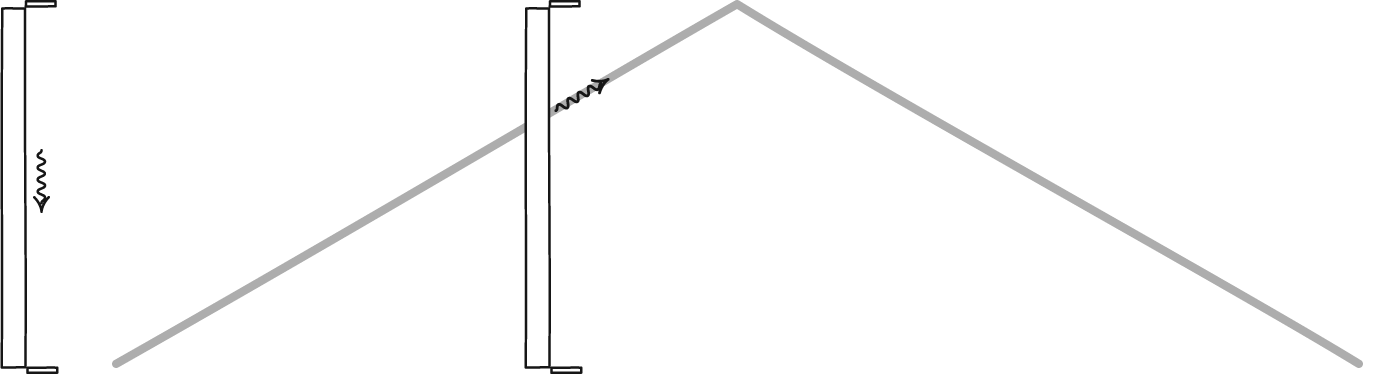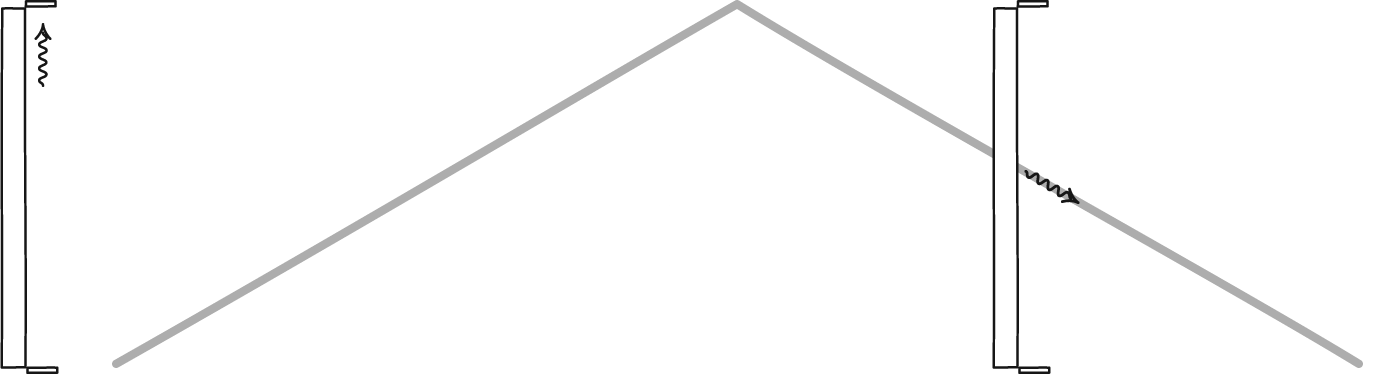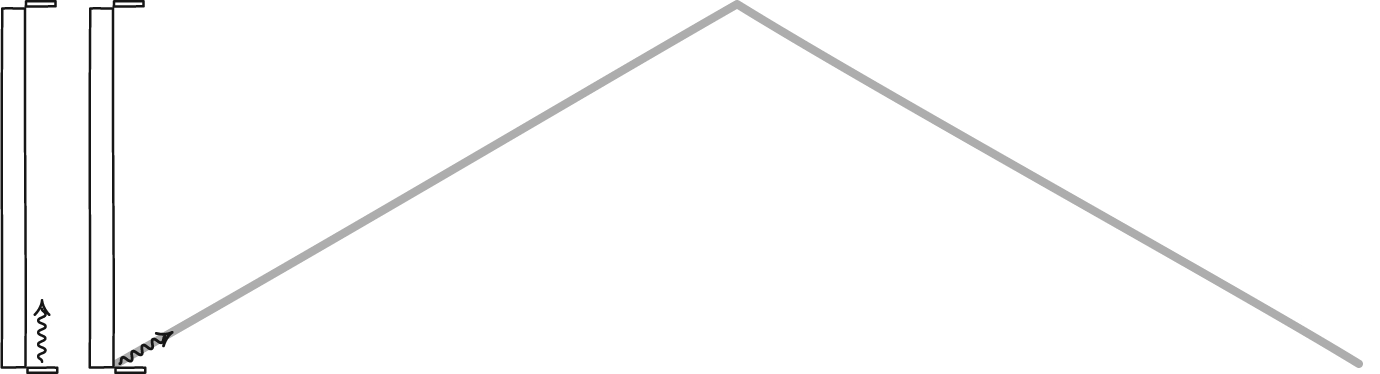
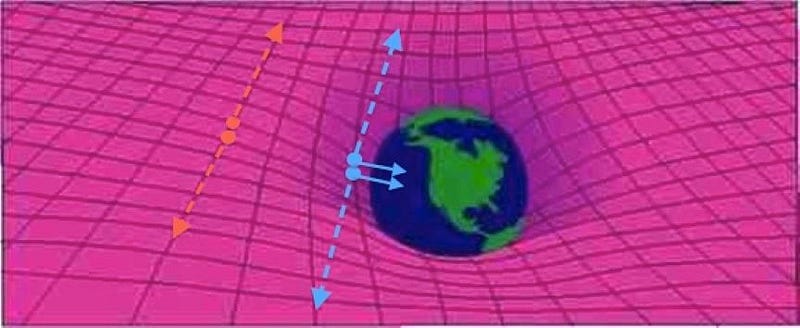
Imagine that you take your particle-antiparticle combination and you started high above the north pole of Earth, at some very high altitude. Because you’re located at the pole, there’s no kinetic energy from the Earth’s rotation where you’re positioned. Instead, owing to your altitude, all of your extra energy is in the form of gravitational potential energy. That, plus the rest mass energy of the particle and antiparticle, are all you start with.

Now, imagine you drop both the particle and antiparticle, and allow them to fall together. As they descend, they’ll both maintain their rest mass energy as defined by E = mc², but their potential energies will transform into kinetic energy: the energy of motion. If you were to measure both the particle and the antiparticle just before they reached the ground, you’d find they had the same amount of energy as they did just before you released them. The only difference is that gravitational potential energy has converted into kinetic energy.

When you look at the above image, where the arrows represent the speeds of the particle-antiparticle pairs in question, all three locations each have the same amount of energy. In the orange case, all of the energy is rest mass plus potential energy; in the blue case, it’s all rest mass plus kinetic energy; in the yellow (intermediate) case, it’s rest mass plus potential plus kinetic, where potential energy is in the process of being converted into kinetic energy.

Now, we can add in one little kink to this otherwise mundane example: at each of these three imagined locations, we can have the particle-antiparticle pair spontaneously annihilate to create two photons. In all three cases, the annihilation will produce two photons of specific, well-defined energies.

But, if we start to think about the energies of the photons produced, these three cases won’t be identical any longer.

1. For the initially orange case, the particle and antiparticle are both at rest, and so when they annihilate, the energy of the two photons created comes exclusively from the rest mass: E = mc².
2. But as the potential energy converts to kinetic energy, that particle-antiparticle pair is now in motion, and when they annihilate, the photon energy comes from both the rest mass of the particle and antiparticle, but also the kinetic energy of the particle and antiparticle in motion. There’s an extra term in the energy, from the particle’s momentum: E = mc² + p²/2m.
3. And if you allowed that particle-antiparticle pair to annihilate just before they hit the ground, there would be no potential energy left; all of it would be converted to kinetic energy, and the photons you produced at the bottom would have the most energy of all.

In order to keep energy conserved, the photons you produce from a particle-antiparticle pair that’s been falling must be more energetic — and bluer in wavelength — than the photons you produce from a particle-antiparticle pair at rest at a high altitude. In fact, we can take the thought experiment one step further, and imagine that we:

• took a particle-antiparticle pair at rest at a high altitude,
• annihilated them to create two photons,
• and then let the two photons fall deeper into the gravitational potential well created by a massive source.

What happens to the photons? If special relativity were correct, they’d remain unchanged, which cannot be correct. Instead, to conserve energy, we have to accept that light must change its wavelength (and hence, frequency and energy, too) as it moves through a gravitational field. If you escape the gravitational field, you get redshifted; if you fall deeper into it, you get blueshifted.

In Einstein’s initial formulation of General Relativity way back in 1916, he mentioned the gravitational redshift (and blueshift) of light as a necessary consequence of his new theory, and the third classical test, after the precession of Mercury’s perihelion (already known at the time) and the deflection of starlight by a gravitational source (discovered during a total solar eclipse in 1919).

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Although a thought experiment is an extremely powerful tool, practical experiments didn’t catch up until 1959, where the Pound-Rebka experiment finally measured a gravitational redshift/blueshift directly. Yet just by invoking the idea that energy must be conserved, and a basic understanding of particle physics and gravitational fields, we can learn that light must change its frequency in a gravitational field.

It’s a good thing that this happens, too! If light remained at the same frequency regardless of where it was in a gravitational field, we could:

1. start by annihilating matter with antimatter on the ground,
2. build a mirror to reflect those photons upwards, away from the gravitational source,
3. re-form those photons back into matter and antimatter (which would only be possible if gravitational redshift weren’t real),
4. and then let them fall back to Earth, where the kinetic energy of their arrival is all “free” energy.

If you don’t like perpetual motion machines or violating the laws of thermodynamics, you could have thought of this yourself and immediately recognized that special relativity wasn’t the full story. Generalizing it to include gravitational physics was what enabled the big leap from special to General Relativity. While we can’t ever predict what nature will do until we put it to an experimental test, a thought-experiment can teach us where to look for hints of new physics. When the technology actually catches up, we always learn something new about the natural world.