This Is Why Dark Energy Is The Biggest Unsolved Problem In The Universe

There are a lot of unsolved mysteries in the Universe, but dark energy is the most confusing. Here’s why.

The majority of the energy in our Universe went completely undiscovered until the late 1990s, and scientists still don’t know what it is. Only 5% of the Universe, in terms of energy, is made out of things we’re familiar with and understand: protons, neutrons, electrons, photons, neutrinos, black holes and even gravitational waves. Of the remainder, 27% is dark matter and 68% ⁠ — the largest amount ⁠ — is in the form of a new, mysterious substance: dark energy.

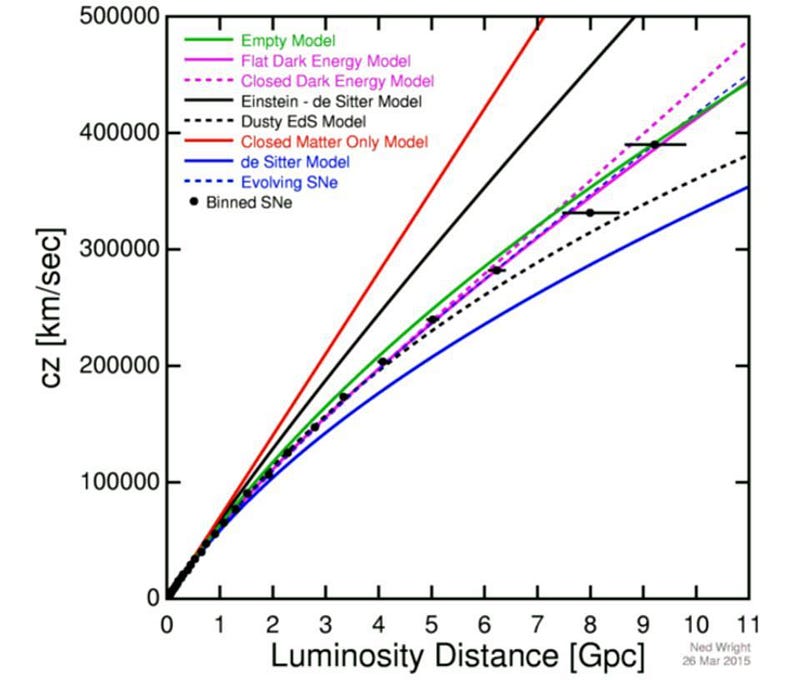
Dark energy was first revealed observationally: by examining the light from ultra-distant signals like supernovae. With measurements of both distance and redshift, scientists concluded that the Universe couldn’t just be made of matter and radiation, but needed a new form of energy that would change the fate of our Universe. Here’s why, more than 20 years later, it’s still the biggest unsolved problem of them all.

The different possible fates of the Universe, with our actual, accelerating fate shown at the right. After enough time goes by, the acceleration will leave every bound galactic or supergalactic structure completely isolated in the Universe, as all the other structures accelerate irrevocably away. We can only look to the past to infer dark energy’s presence and properties, which require at least one constant, but its implications are larger for the future. (NASA & ESA)

If you want to know what the Universe is made of, all you have to do is measure the distances to and the redshifts of a variety of different objects in the Universe. The redshift you measure will be a combination of how quickly the object is moving through space (typically hundreds or a few thousand km/s) and how much the Universe has expanded since the light was emitted from a distant source, while the distance can be inferred by measuring either the apparent brightness or apparent angular size of an object, compared with a known actual, intrinsic brightness or size.

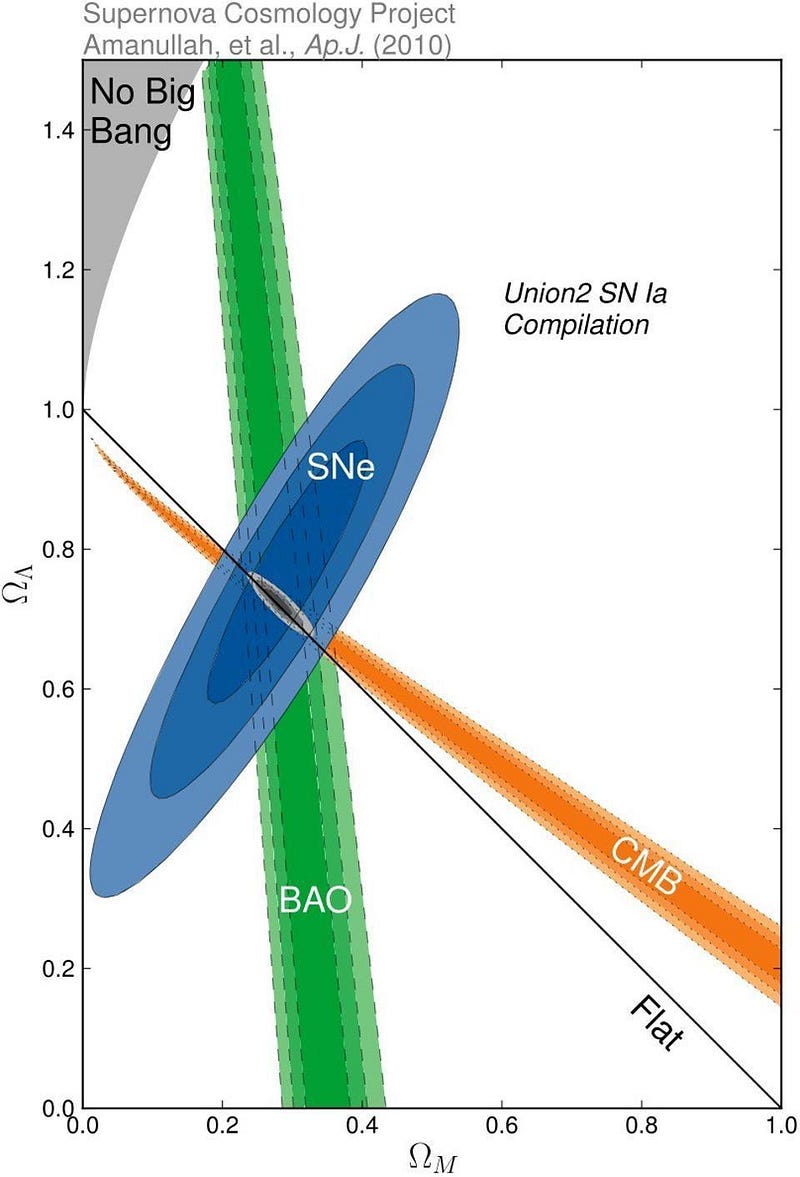
When we combine all the observations we have — from supernovae, from large-scale structure, from the fluctuations in the cosmic microwave background, etc. — they all point to a single, unified picture of the Universe: with 5% normal matter, 27% dark matter, and 68% dark energy.

A plot of the apparent expansion rate (y-axis) vs. distance (x-axis) is consistent with a Universe that expanded faster in the past, but where distant galaxies are accelerating in their recession today. This is a modern version of, extending thousands of times farther than, Hubble’s original work. Note the fact that the points do not form a straight line, indicating the expansion rate’s change over time. The fact that the Universe follows the curve it does is indicative of the presence, and late-time dominance, of dark energy. (NED WRIGHT, BASED ON THE LATEST DATA FROM BETOULE ET AL. (2014))

From a theoretical point of view, the way we make sense of these observations is extraordinarily straightforward. On the largest cosmic scales, our Universe is the same in all directions and at all locations. You might examine the cosmic web and note that you can go millions of light-years in any direction from a galaxy before encountering another one, but those scales aren’t large enough to see how uniform things truly are. Our actual observable Universe contains about 400,000 Gly³ (where 1 Gly is one billion light-years), and on scales of more than a few billion cubic light-years, things are truly about 99.99% uniform.

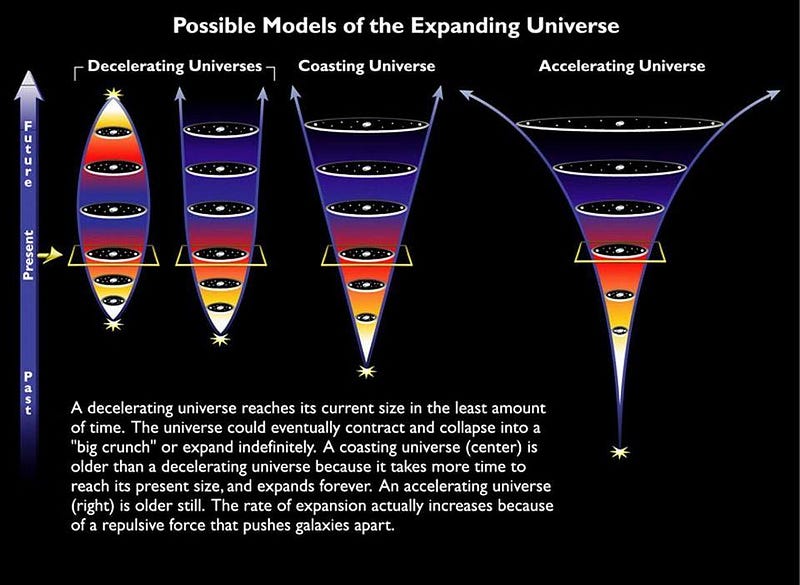
When the Universe behaves as though it’s the same in all directions and locations, you can write down an exact solution for how the Universe will behave: an expansion/contraction factor on the left and all the matter-and-energy terms on the right. These are the rules that govern the expanding Universe, and by measuring how that rate changes over time, we can determine what’s in the Universe, how much, and how it behaves.

A photo of me at the American Astronomical Society’s hyperwall in 2017, along with the first Friedmann equation at right. The first Friedmann equation details the Hubble expansion rate squared on the left hand side, which governs the evolution of spacetime. The right side includes all the different forms of matter and energy, along with spatial curvature, which determines how the Universe evolves in the future. This has been called the most important equation in all of cosmology, and was derived by Friedmann in essentially its modern form back in 1922. (PERIMETER INSTITUTE / HARLEY THRONSON)

Different data sets place different constraints on what’s in the Universe, but by combining them and seeing where they overlap, we can see if there’s one set of parameters that will fit all of the disparate types of data at once.

That’s where the “concordance model” in cosmology comes from, of a Universe that’s:

expanding at around 67-to-74 km/s/Mpc today,
where the expansion is presently dominated (68%) by dark energy,
where the Universe is spatially flat,
where the rest of the Universe’s energy (32%) is mostly in the form of matter (both normal and dark),
and where the Universe is approximately 13.8 billion years old, since the hot Big Bang first occurred.

Even with recent controversies and tensions, this remains the consensus picture of the Universe: the one that’s consistent with the full suite of data we have, even including the present uncertainties.

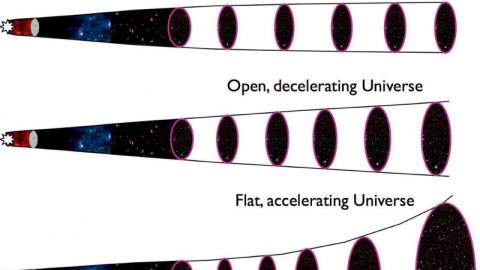
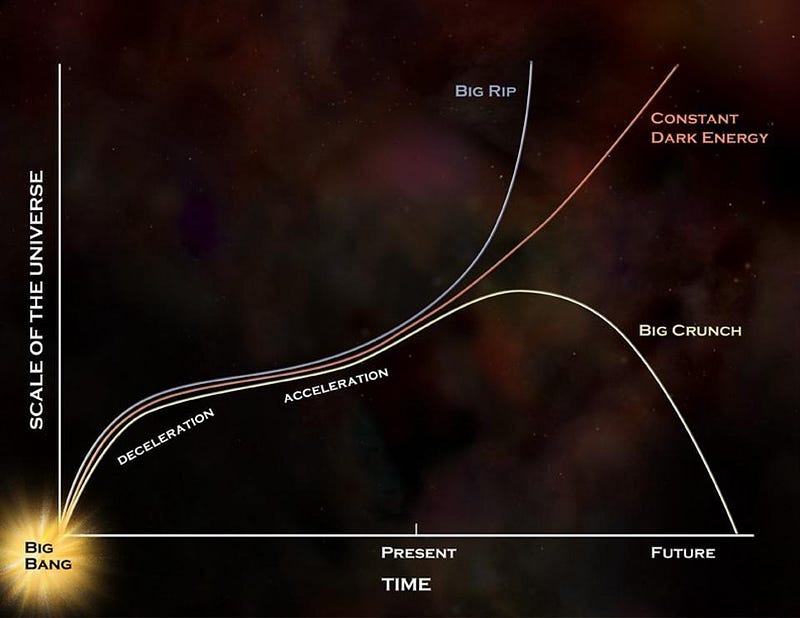
Constraints on the total matter content (normal+dark, x-axis) and dark energy density (y-axis) from three independent sources: supernovae, the CMB (cosmic microwave background) and BAO (which is a wiggly feature seen in the correlations of large-scale structure). Note that even without supernovae, we’d need dark energy for certain, and also that there are uncertainties and degeneracies between the amount of dark matter and dark energy that we’d need to accurately describe our Universe. (SUPERNOVA COSMOLOGY PROJECT, AMANULLAH, ET AL., AP.J. (2010))

It might strike you as bizarre that the majority of the energy in the Universe would not only be invisible (or dark), but that it isn’t even a form of matter! Matter normally clumps and clusters together, as masses are gravitationally attracted to other masses; when enough matter gets together in one spot, it can overcome the expansion of the Universe and form stars, galaxies, and groups/clusters of galaxies. In a Universe dominated by matter, structure grows larger and larger and becomes more complex and web-like as time goes on.

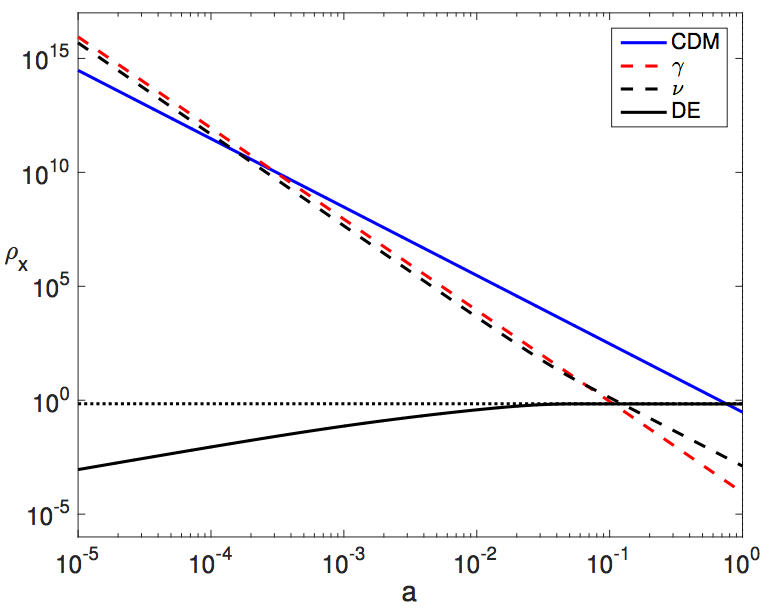
But in a Universe that also has copious amounts of dark energy, there will be a limit to the size and complexity of that web. The dark energy we see behaves as though it’s a form of energy inherent to the fabric of space itself. As the Universe expands, matter gets less dense (as volume increases), radiation gets both less dense (as volume increases) and less energetic (as light redshifts), but dark energy’s energy density always remains constant. After billions of years, the density of both radiation and matter drops below the dark energy density, leading to the accelerated expansion we observe today.

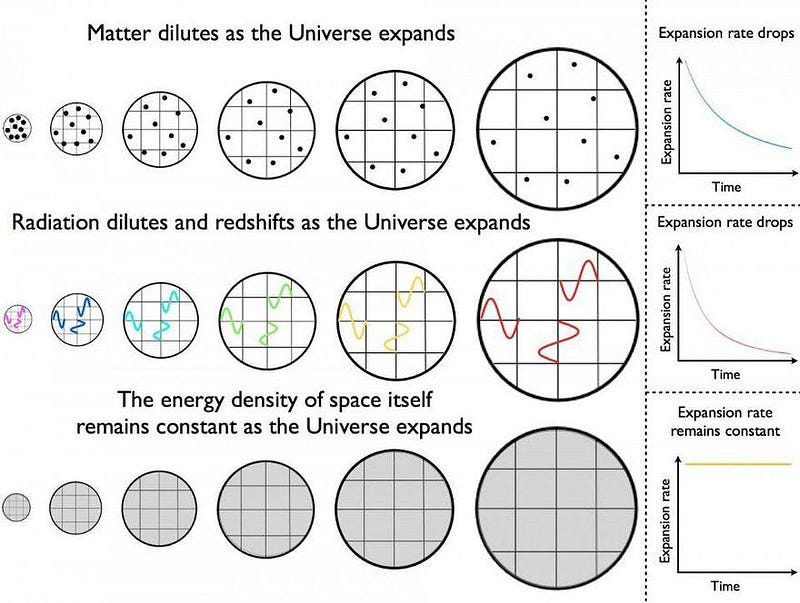
While matter (both normal and dark) and radiation become less dense as the Universe expands owing to its increasing volume, dark energy is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant. If dark energy changes over time, we could discover not only a possible solution to this conundrum concerning the expanding Universe, but a revolutionary new insight concerning the nature of existence. (E. SIEGEL / BEYOND THE GALAXY)

One of the goals of modern observational cosmology is to fully describe dark energy by measuring as many different properties about the expanding Universe that are capable of probing its nature. As we collect large numbers of distant type Ia supernovae, better measure the large-scale clustering properties of the cosmic web at early, intermediate, and late times, and extract greater details from the cosmic microwave background’s fluctuations and polarization, we can better hone in on exactly how to describe dark energy.

It could behave as a cosmological constant, which would mean it was a form of energy inherent to space itself, or it could behave in a more complex fashion: as a general form of energy with its own unique (and possibly dynamical, ever-changing) equation of state. However, observations thoroughly rule out a Universe governed by General Relativity with no dark energy at all.

Instead of adding in a cosmological constant, modern dark energy is treated as just another component of energy in the expanding Universe. This generalized form of the equations clearly shows that a static Universe is out, and helps visualize the difference between adding a cosmological constant and including a generalized form of dark energy. (© 2014 THE UNIVERSITY OF TOKYO; KAVLI IPMU)

The way we conventionally describe dark energy is through a single parameter: w, known as the equation of state. In physics, w relates the energy density of any form of energy to the pressure of that form of energy. For normal matter that moves at negligible speeds relative to the speed of light, w = 0, meaning that both normal matter and dark matter are pressureless.

Radiation, on the other hand, does exert a pressure: w = +⅓. This positive pressure leads to an expansion rate that drops more quickly with time: when the Universe is radiation-dominated, its expansion rate declines more quickly than a matter-dominated (with w = 0) Universe. You can also have a Universe with w = -⅓ (dominated by cosmic strings or spatial curvature), with w = -⅔ (dominated by domain walls), or by a cosmological constant: with w = -1. While other values are possible, as well as changes in w with time, we’ve constrained w to equal -1 exactly, with an uncertainty of about 10% at most.

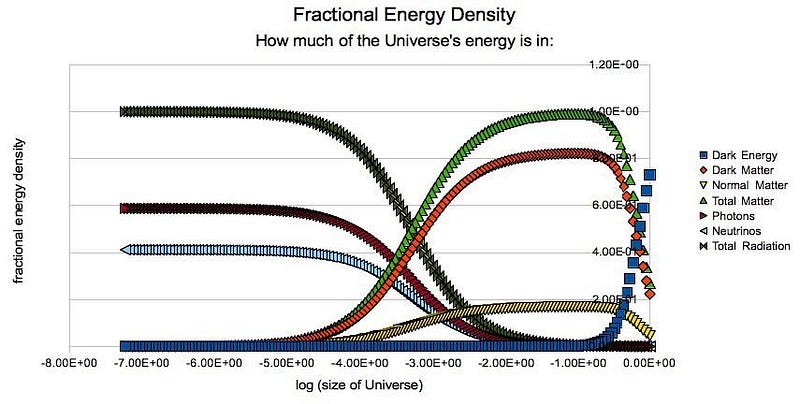
The relative importance of dark matter, dark energy, normal matter, and neutrinos and radiation are illustrated here. While dark energy dominates today, it was negligible early on. Dark matter has been largely important for extremely long cosmic times, and we can see its signatures in even the Universe’s earliest signals. (E. SIEGEL)

Theoretically, the simplest models for a new form of energy to the Universe happen in increments for w of ⅓; the fact that dark energy is very close to -1.00 teaches us that it’s more consistent with a cosmological constant (where w = -1 exactly) than any other forms of energy we understand.

The cosmological constant, in General Relativity, is interesting because it’s the only form of energy you can add to the Einstein equations (and hence, the Friedmann equations) in addition to the types of matter-and-energy found in the Universe. It also shows up in quantum field theory: as the energy inherent to empty space itself. If we were capable of calculating the contributions of all the different particles and fields allowed to exist in this Universe — and how they applied to the vacuum of space itself — we’d expect to get the value for the zero-point energy of space itself, and therefore, the value of our Universe’s cosmological constant.

Visualization of a quantum field theory calculation showing virtual particles in the quantum vacuum. (Specifically, for the strong interactions.) Even in empty space, this vacuum energy is non-zero. (DEREK LEINWEBER)

“Okay,” you say, “we know how to begin calculating individual terms that contribute to the quantum vacuum, so what are they?” And you do those calculations, and start getting answers that are far, far too big to be correct: some 120 orders of magnitude greater than observational constraints allow.

When you start looking at why, it’s because the value of the cosmological constant is proportional to a mass/energy value raised to the 4th power, and the “default” value that goes in there is a combination of three fundamental constants: c (the speed of light), h (Planck’s constant), and G (the gravitational constant). Construct a mass/energy out of those and the value you get is about ~10¹⁹ GeV, known as the Planck mass/energy.

This is a tremendous mismatch, and so many theoretical inventions are done in such a way so that dark energy gets explained through a different mechanism.

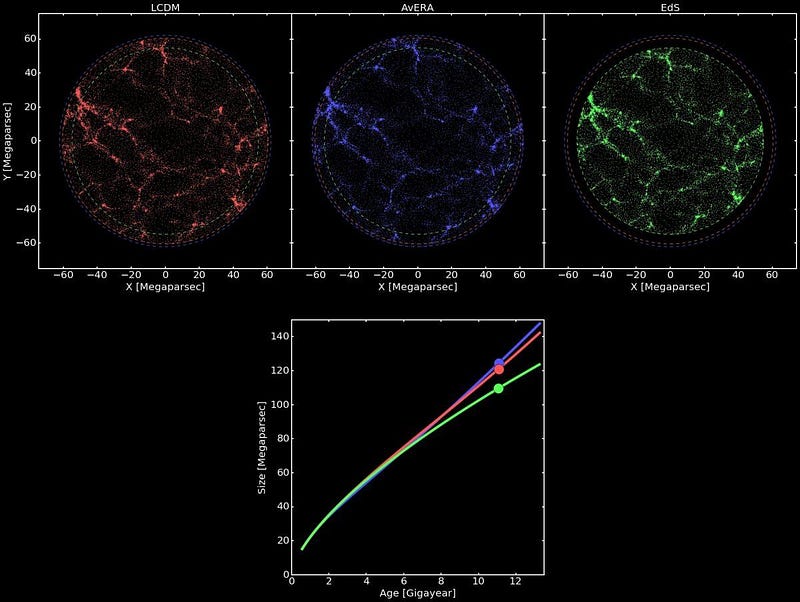
An illustration of how the radiation (red), neutrino (dashed), matter (blue), and dark energy (dotted) densities change over time. In a new model proposed some years ago, dark energy would be replaced by the solid black curve, which is heretofore indistinguishable, observationally, from the dark energy we presume. (FIGURE 1 FROM F. SIMPSON ET AL. (2016), VIA HTTPS://ARXIV.ORG/ABS/1607.02515)

You can try throwing out General Relativity and modify gravity instead, which enables you to introduce a number of new free parameters that could explain dark energy instead of a cosmological constant.

You can introduce a new field to the Universe, which couples to the various forces or interactions in a number of possible ways, enabling behaviors that would cause the Universe’s expansion rate to behave in the ways we observe.

You can construct a model where the conditions that existed during the inflationary phase (our only other known period of exponential expansion) are connected to today’s dark energy.

Or you could introduce a new idea that leads to different effects from what we typically expect in our Universe. Any model that offers significantly different observables than a cosmological constant can be put to the test.

A Universe with dark energy (red), a Universe with large inhomogeneity energy (blue), and a critical, dark-energy-free Universe (green). Note that the blue line behaves differently from dark energy. New ideas should make different, observably testable predictions from the other leading ideas. And ideas which have failed those observational tests should be abandoned once they reach the point of absurdity. (GÁBOR RÁCZ ET AL., 2017)

Of course, there’s no motivation as to why any of these theoretical contortions would be necessary, as any of these modifications still need to reckon with the cosmological constant and the zero-point energy of space in quantum field theory. As of today, they all hand-wave the issue away, claiming that the “true” vacuum expectation value is likely zero, and ascribing what we observe as dark energy to an additional ad hoc effect.

Sure, this allows you the freedom — by introducing whatever gravity modification, whatever new field, whatever joint model of inflation + dark energy, or whatever other idea you invent — to get whatever fate of the Universe you like out of it.

But there is no motivation for any of these steps, even though they are theoretically fashionable these days. The reality is that every indicator we have shows that dark energy is no different than a straightforward cosmological constant. Anything else isn’t ruled out, but is motivated by nothing more than wishful thinking and theoretically imaginative musings.

The far distant fates of the Universe offer a number of possibilities, but if dark energy is truly a constant, as the data indicates, it will continue to follow the red curve, leading to the long-term scenario described here: of the eventual heat death of the Universe. (NASA / GSFC)

What many people have noticed, however, is that perhaps a calculation that results in putting the Planck mass/energy into the value of the cosmological constant is completely wrongheaded. If instead of 10¹⁹ GeV, we placed in a mass/energy that was closer to 0.001-to-0.01 eV that we’d take to the 4th power, we’d get a value of the cosmological constant that matched what we observe in our Universe.

What’s very, very interesting about this mass range is there are two classes of particles that naturally fall right into it:

the neutrino; from a variety of measurements, we know that neutrinos have slightly different masses from one another, and that the differences between the different species fall within this range.
the axion, which is a theoretical particle and a dark matter candidate; many variations of the axion could have a rest mass in the micro-eV to milli-eV range.

If there’s new physics appearing at this low-energy scale, its contributions to the quantum vacuum could also explain the dark energy puzzle.

The XENON1T detector, with its low-background cryostat, is installed in the centre of a large water shield to protect the instrument against cosmic ray backgrounds. This setup enables the scientists working on the XENON1T experiment to greatly reduce their background noise, and more confidently discover the signals from processes they’re attempting to study. XENON is not only searching for heavy, WIMP-like dark matter, but other forms of potential dark matter, including light candidates like dark photons and axion-like particles. (XENON1T COLLABORATION)

The true fact of the matter is that, observationally, dark energy is behaving as though it’s a form of energy inherent to the fabric of space itself. WFIRST, NASA’s flagship astrophysics mission of the 2020s (after James Webb), should allow us to reduce the measured constraints on w down to the 1-or-2% level. If it still looks indistinguishable from a cosmological constant (with w = -1) then, we’ll have no choice but to reckon with the quantum vacuum itself.

Why does empty space have the properties that it does? Why is the zero-point energy of the fabric of the Universe a positive, non-zero value? And why does dark energy have the behavior we observe it to have, rather than any other?

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

There are an infinite number of models we can cook up to describe what we see, but the simplest model — of a non-zero cosmological constant — requires no additions or modifications to match the data. Until we make progress on understanding the quantum vacuum itself, dark energy will remain the biggest unsolved puzzle in all of modern theoretical physics.

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.