This Is How Astronomers Know The Age Of The Universe (And You Can, Too)

The hot Big Bang occurred 13.8 billion years ago, and there’s no other possible answer consistent with what we know today.
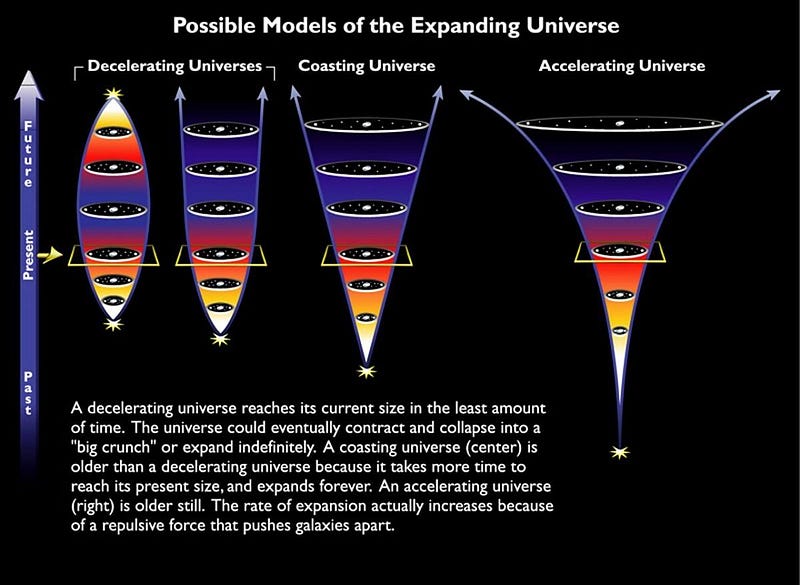
Conceptually, it might seem like the simplest idea in existence to determine the age of the Universe. Once you figure out that the Universe is expanding, all you need to do is measure the expansion rate today and use the laws of physics to determine how the expansion rate must have changed over time. Instead of extrapolating forward to determine the fate of the Universe, you do the calculating backwards instead, and go all the way back until you achieve the conditions of the hot Big Bang itself.
This obvious method not only works, but it remains the best way we have to calculate the Universe’s age even today. Yet it’s very easy to go awry, as there are many simplifying assumptions you can make that will give you an easy answer that isn’t necessarily correct, including errors that even a Nobel Laureate made earlier this year. Here’s how you, too, can figure out the age of the Universe.

The first place to start is with the expanding Universe itself and the one parameter we’ve strived to measure longer than any other: the Hubble constant. On the largest scales, the galaxies we find in the Universe obey a very simple relation between the two observable quantities of distance and redshift, where the farther away an object is from us, the greater its measured redshift will be.
Remarkably, the law that relates them is extremely straightforward: the recession speed that you would infer from a galaxy’s redshift equals the distance to that galaxy multiplied by the Hubble constant. Even more remarkably, that constant has the same value for pretty much every galaxy we measure, particularly for galaxies within a few billion light-years of us. Even though there are additional cosmic motions inherent to each galaxy induced by gravitational effects, this law remains true when you average over all the galaxies you can find.
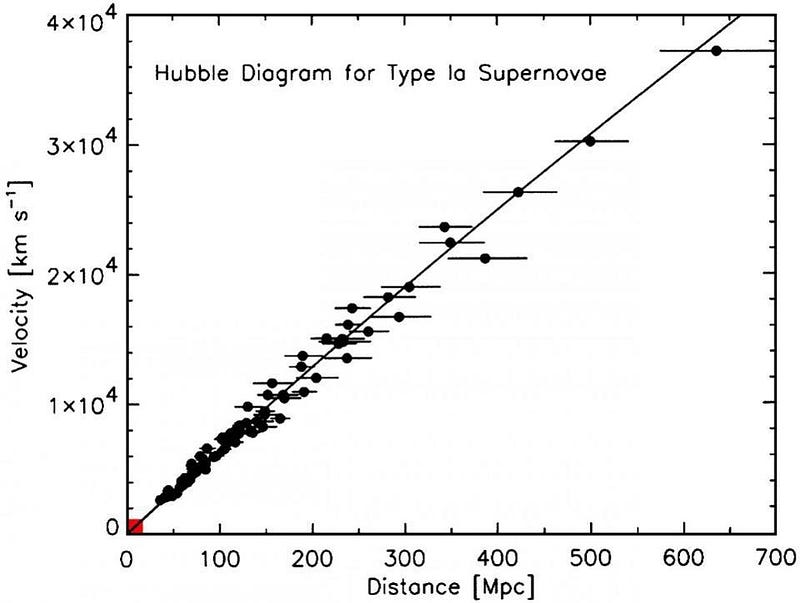
So what do we measure the Hubble constant to be? It depends on how you measure it, since:
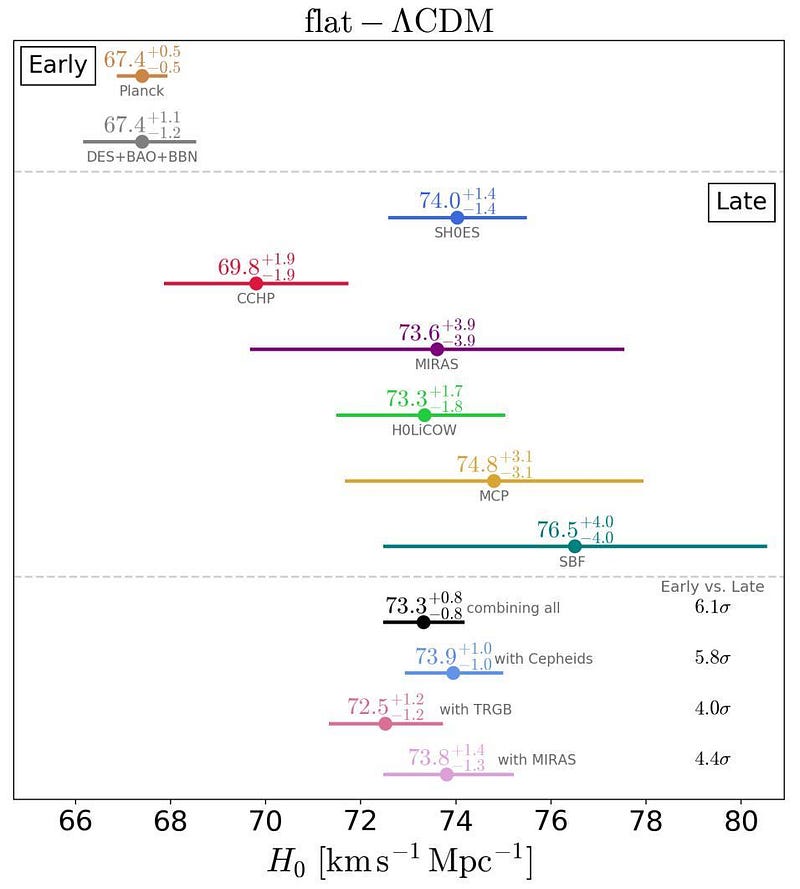
- if you measure it by using signals that were imprinted all the way back in the earliest stages of the Big Bang, you get a value for the Hubble constant of 67 km/s/Mpc, with an uncertainty of 1–2%,
- but if you measure it by measuring individual light sources that don’t arrive until the Universe is already billions of years old, you obtain a value for the Hubble constant of 73 km/s/Mpc, with an uncertainty of just 2–3%.
Why these two values don’t match — and why they give such different, mutually inconsistent answers — is one of the major conundrums of modern cosmology.
However, the very astute among you will notice something about the Hubble constant itself: it comes in units that are a speed (km/s) per unit distance (Mpc, where 1 megaparsec is about 3.26 million light-years). If you look at a galaxy that’s 100 Mpc away, you’d expect it to recede away ten times faster than one only 10 Mpc away, but only one-tenth as fast as a galaxy 1,000 Mpc away. That’s the simple power of the redshift-distance relation.
But there’s another way to manipulate the Hubble constant: to recognize that a speed (distance-per-time) per (divided by) unit distance (distance) is the same as units of inverse time. What could the physical meaning of that “inverse time” correspond to? Perhaps, you might reasonably imagine, it could correspond to the age of the Universe.
There are approximately 3.1 × 10¹⁹ kilometers in one megaparsec, which means that if you turn the Hubble constant into an inverse time, you find some fascinating things.
- The “time” that a value of 67 km/s/Mpc corresponds to is equivalent to 14.6 billion years.
- The “time” that a value of 73 km/s/Mpc corresponds to is equivalent to 13.4 billion years.
These are both almost equal to the accepted age of the Universe, but not quite. In addition, they’re both almost equal to one another, but differ by approximately the same amount that the two estimates for the Hubble constant differ by: 9% or so.
However, you cannot simply change the age of the Universe by changing the Hubble constant, and there’s a subtle but vital reason why this is so.

The value of the Hubble constant today isn’t simply the inverse of the value of the age of the Universe, even though the units work out to give you a measure of time. Instead, the expansion rate that you measure — the Hubble constant today — must balance the sum total of every form of energy that contributes to the Universe’s composition, including:
- normal matter,
- dark matter,
- neutrinos,
- radiation,
- dark energy,
- spatial curvature,
- and anything else you can cook up.
The equation that governs the expanding Universe (shown above) can be solved exactly in some simple cases.
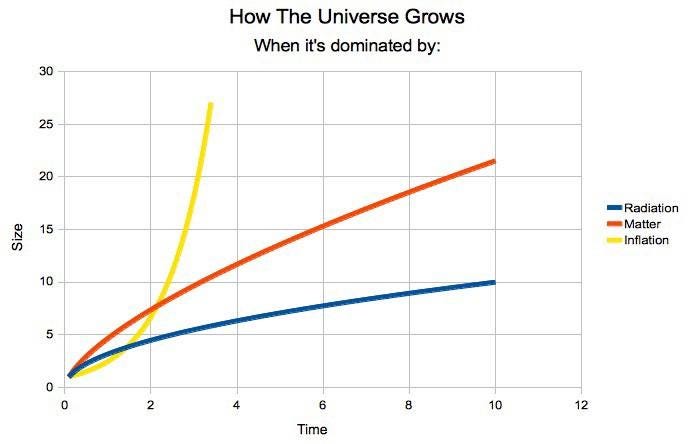
If your Universe is exclusively made up of radiation, you find that the Hubble constant multiplied by the age of the Universe since the Big Bang equals ½, exactly. If your Universe is exclusively made up of matter (normal and/or dark), you find that the Hubble constant multipled by the age of the Universe equals ⅔, exactly. And if your Universe is entirely made of dark energy, you’ll find that there is no exact answer; the value of the Hubble constant multiplied by the age of the Universe always continues to increase (towards infinity) as time goes on.
This means that if we want to accurately calculate the age of the Universe, we can do it, but the Hubble constant alone isn’t enough. In addition, we also need to know what the Universe is made out of. Two imagined Universes with the same expansion rate today but made out of different forms of energy will have different expansion histories and, therefore, different ages from one another.
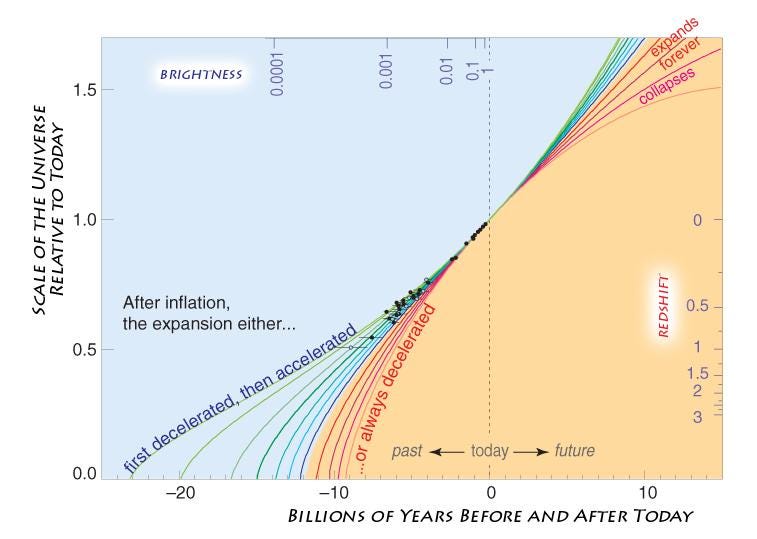
So, to find out how old the Universe actually is since the onset of the hot Big Bang, all we have to do is determine the expansion rate of the Universe and what the Universe is made out of. There are a variety of methods that we can use to make this determination, but there’s one vital thing we have to remember: many of the ways we have of measuring one parameter (like the expansion rate) are dependent on our assumptions about what the Universe is made out of.
In other words, we cannot assume that the Universe is made out of a certain amount of matter, a certain amount of radiation, and a certain amount of dark energy in a way that’s independent of the expansion rate itself. Perhaps the most powerful way to illustrate this is to look at the leftover glow from the Big Bang itself: the Cosmic Microwave Background.
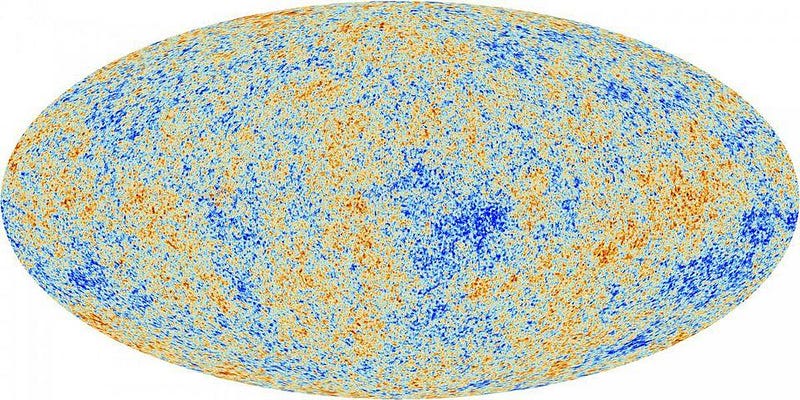
This, above, is a map of the fluctuations in the Cosmic Microwave Background. Overall, every direction in the Universe displays the same average temperature as every other direction: approximately 2.725 K. When you subtract that mean value out, you get the pattern that you see above: the fluctuations, or departures from the average temperature.
Where you see dark blue or dark red spots, those are regions where the temperature fluctuations are largest: approximately 200 microkelvin colder (for blue) or hotter (for red) than the mean value. These fluctuations exhibit particular patterns in their magnitude on a variety of angular scales, with the fluctuations rising in magnitude down to some particular angular scale of about 1 degree, then decreasing and increasing in an oscillatory fashion. Those oscillations tell us some vital statistics about the Universe.
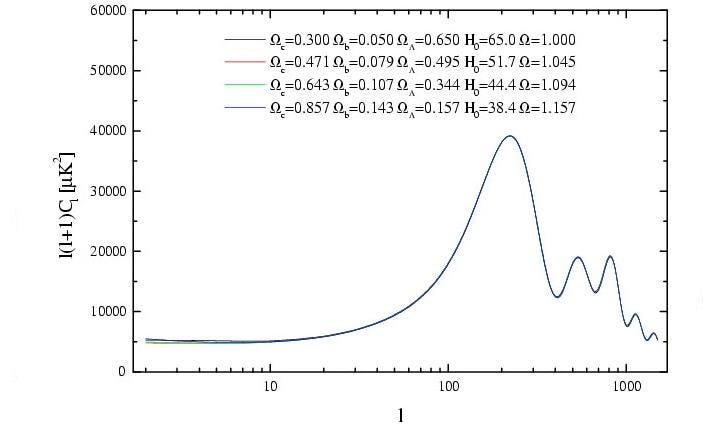
What’s most important to realize is that there are many possible combinations of values that can fit any particular graph. For example, given the fluctuations we see, we can have a Universe with:
- 4% normal matter, 21% dark matter, 75% dark energy and a Hubble constant of 72,
- 5% normal matter, 30% dark matter, 65% dark energy and a Hubble constant of 65,
- or 8% normal matter, 47% dark matter, 49% dark energy, -4% curvature and a Hubble constant of 51.
You will notice a pattern here: you can have a larger Hubble constant if you have less matter and more dark energy, or a smaller Hubble constant if you have more matter and less dark energy. What’s remarkable about these combinations, however, is that they all lead to almost exactly the same age for the Universe since the Big Bang.
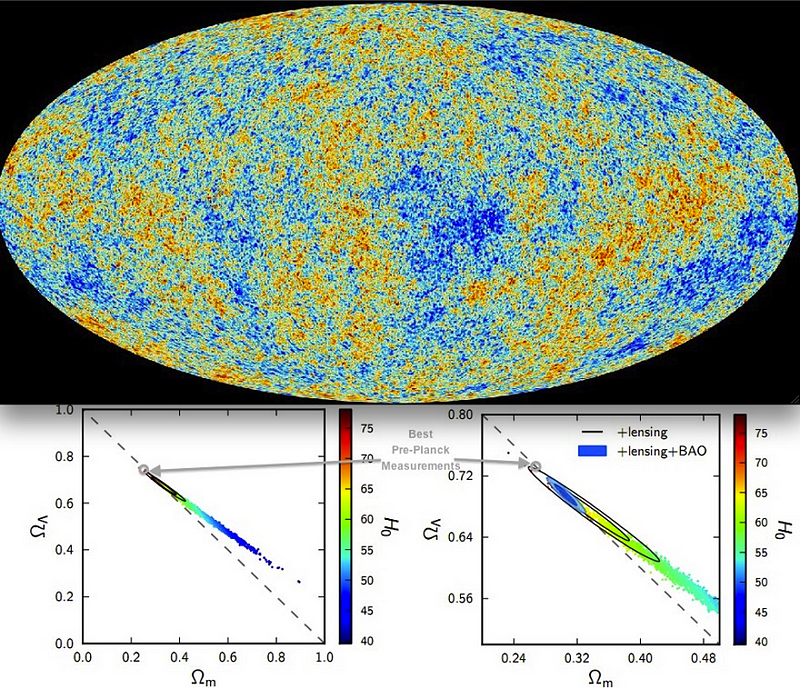
The reason that we can claim the Universe is 13.8 billion years old to such enormous precision is driven by the full suite of data that we have. A Universe that expands more quickly needs to have less matter and more dark energy, and its Hubble constant multiplied by the age of the Universe will have a larger value. A slower-expanding Universe requires more matter and less dark energy, and its Hubble constant multiplied by the age of the Universe gets a smaller value.
However, in order to be consistent with what we observe, the Universe can be no younger than 13.6 billion years and no older than 14.0 billion years, to more than 95% confidence. There are many properties of the Universe that are indeed in doubt, but its age isn’t one of them. Just make sure you take the Universe’s composition into account, or you’ll wind up with a naive — and incorrect — answer.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





