The odds of your unlikely existence were not infinitely small

If every infinite outcome were equally likely, we’d never come to be.
“Logic takes care of itself; all we have to do is to look and see how it does it.”
–Ludwig Wittgenstein
In order for you to exist, a great many unlikely events needed to unfold in exactly the way that they did. The exact sperm cell and egg cell needed to meet to create you with the DNA sequence that encoded you, and brought you into existence; a one-in-250 million chance for a sperm cell alone. That needed to happen each time in an unbroken string for millions of generations of your ancestors, going back to well before they were human beings or even hominids of any type. Other unlikely events needed to occur as well: life needed to take hold on Earth, Earth needed to form as a habitable planet with the right ingredients for life out of the ashes of previously dead stars, the laws of physics needed to be such that they permitted life, and the Universe itself must have unfolded in such a way as to make all of this possible.
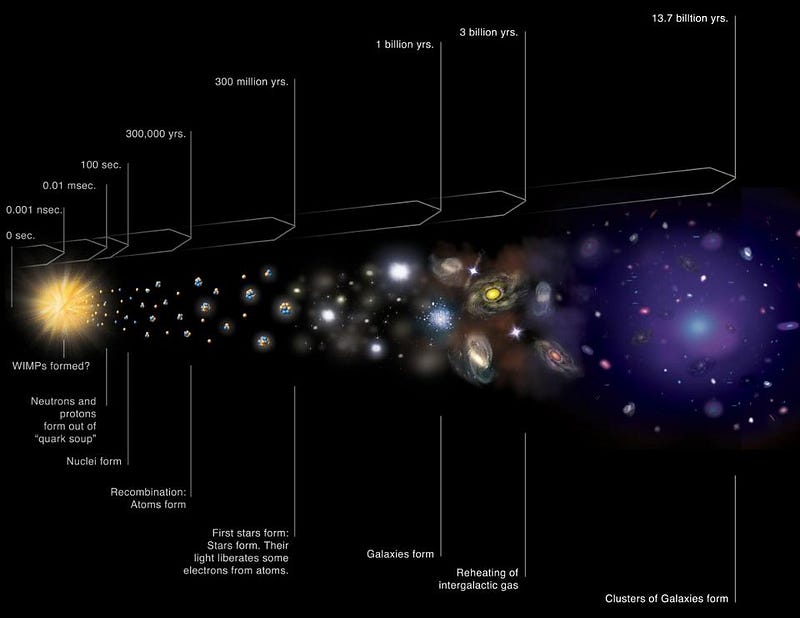
Yet there’s one thing we can be sure of in this entire series of unlikely events, occurring one after the other: nothing that occurred at any point had an infinitesimal likelihood. Instead, every single event, including:
- the mutations and meiosis crossovers in the DNA of each of your ancestors,
- the survival of every one of them to reproductive age,
- the finding of the particular mate needed to give rise to the next generation of your particular ancestors,
- the creation of this exact planet with the exact extinction history that it’s had,
- the formation of stars and galaxies in the Milky Way to create the environment in which Earth formed,
- the creation of the original, initial density conditions of the Universe that make it possible for gravity to create us,
- the realization of the laws of nature that they would be exactly sufficient to create us,
- and that our Universe would have come to exist out of the great abyss of nothingness that came before,
must have had finite odds of occurring. Even the emergence of our Universe from the Multiverse couldn’t have had an infinitely small probability.

How do we know this, you ask? It isn’t physics that tells us this is so, but rather a more fundamental theorem about basic probability itself: Bayes’ theorem. This mathematical idea is devastatingly simple, but its consequences are incredibly complex. On its own, Bayes’ theorem is simply a rule to tell you the probability that something is true, given knowledge of conditions that are related to that thing you’re trying to measure. For example, perhaps you’re hungry right now and perhaps you’re not, and one possibly related factor is the time of day. If you know the time of day and the time of day is related to your hunger, you can more accurately assess whether you’re likely to be hungry or not, probabilistically, than if you didn’t know the time of day. Bayes’ theorem tells you that and a whole lot more.
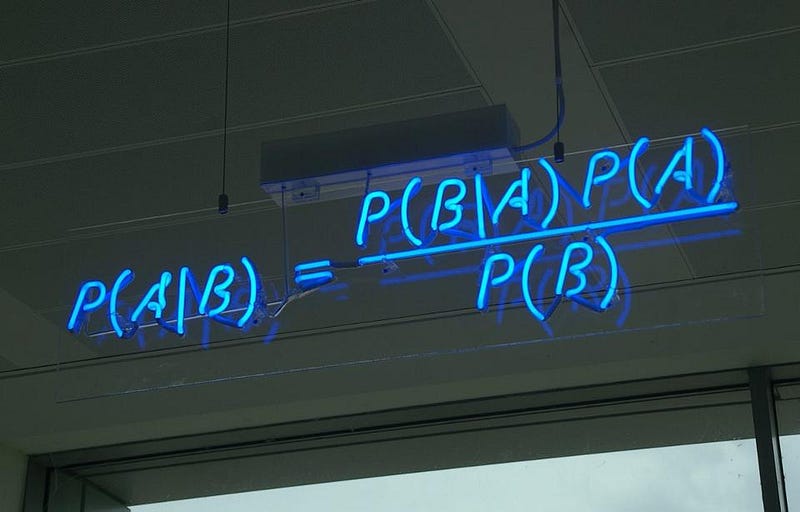
What it does is take any two events, like being hungry (A) and the time of day (B), and relates them by saying:
The probability that A is true if B is given is equal to the probability that B is true if A is given, multiplied by the probability that A is true (independent of B) and divided by the probability that B is true (independent of A).
You can apply that to your hunger based on time, the creation of you based on your biological parents’ genetic material, the existence of Earth based on the interstellar environment where our Solar System formed, or the existence of this Universe based on the conditions that came beforehand. Bayes’ theorem is a mathematical rule that can be applied to any system at all, in principle.
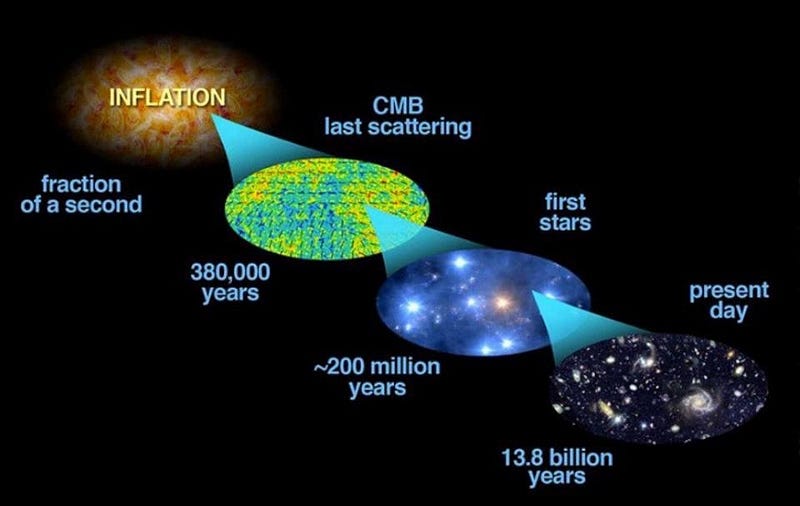
But there’s a fun, important, and underappreciated consequence of Bayes’ theorem that can tell us something vital about any of these steps: the odds of any one of them happening, no matter how small, could not have been infinitesimal. If you want to create our Universe with our laws of physics, our local group, our Sun, our Earth, and every one of us, given all the conditions that existed before the Big Bang, that probability may be very, very small, but it can’t be infinitely small. If it were, our model for the conditions that existed before the Big Bang could be ruled out immediately, with no need to gather data or make measurements.

The reason is that the probability of A not happening, given B, must then be equal to 1, or 100%. If the probability of A happening (regardless of B) goes to zero, then the probability of “not A” happening goes to 1. At a fundamental level, our Universe is based in probabilities, as quantum mechanics uncomfortably taught us in the 20th century. It’s only the act of observing, interacting, measuring or otherwise “determining” the state of a system that forces any system into a particular state. With every measurement we make, we can be sure that the outcome of our experiment, however unlikely, still had a finite, non-zero probability of occurring.
Scientists often argue over cosmic inflation, the model for the origin of our Universe, with some contending that a major problem of inflation is that it gives an infinite number of possible outcomes, all of which are equally likely. But if that were true, and the odds of a Universe turning out like ours were completely infinitesimal, then that model could be immediately ruled out. If there were an infinite number of other possible outcomes that occurred 100% of the time, then there would be no way to obtain our own Universe.
This is true for all types of probabilities! So the next time something unlikely happens, or you realize that something very unlikely must have already occurred, remember that no matter how unlikely it is, the odds of it happening weren’t infinitely small. Its existence, just like our existence, already disproves that possibility!
Thanks to Eiichiro Komatsu, Ben Wandelt and many others for publicly making and sharing this line of reasoning.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.




