The Invisible Mountains of Earth

How gravity teaches us that the mountains we see extend far underground.
“Journalists often ask me when I go to the field, ‘What do you expect to find?’ And my answer always is, ‘The unexpected,’ because we’re just looking at the tip of the iceberg; we’ve just scratched the surface.” –Donald Johanson
Imagine yourself at the surface of Earth, measuring the acceleration due the Earth’s gravity. There are a number of good ways to do it:
- measure the speed of an object in free-fall,
- measure the period of a fixed-length pendulum,
- or simply to time how long it takes something to fall a certain distance,
among many others. And if you’re willing to take on the most advanced modern technology, you can simply carry an accelerometer around with you.

You might’ve learned — in some long-ago physics class — that objects at the surface of the Earth all accelerate downwards, towards the Earth’s center, at 9.81 m/s^2 (or 32 feet/s^2), without fail. But as it turns out, that’s only the average acceleration summed over all the points on Earth’s surface. In reality, there’s some substantial variation, and there are four reasons why.
Three of them make a lot of sense, but the final one’s a little less intuitive, and makes all the difference in the world. Let’s find out what’s going on.
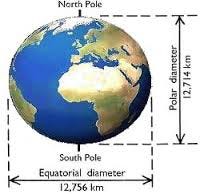
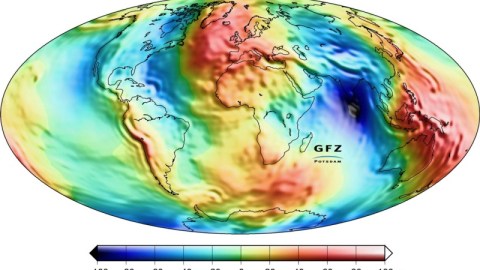
1.) The Earth is rotating. This is one of the easiest ones. If the Earth were stationary and not rotating at all, you can imagine we’d be just a perfect sphere. But the faster you spin us up, the more we’ll bulge at the equator and get compressed around the poles. Rather than forming a plenisphere, or a perfectly round object, Earth more closely resembles an oblate spheroid, where our equatorial radius is some 31 kilometers larger than our polar radius.
The Earth doesn’t even rotate all that fast, as far as worlds in our Solar System goes.
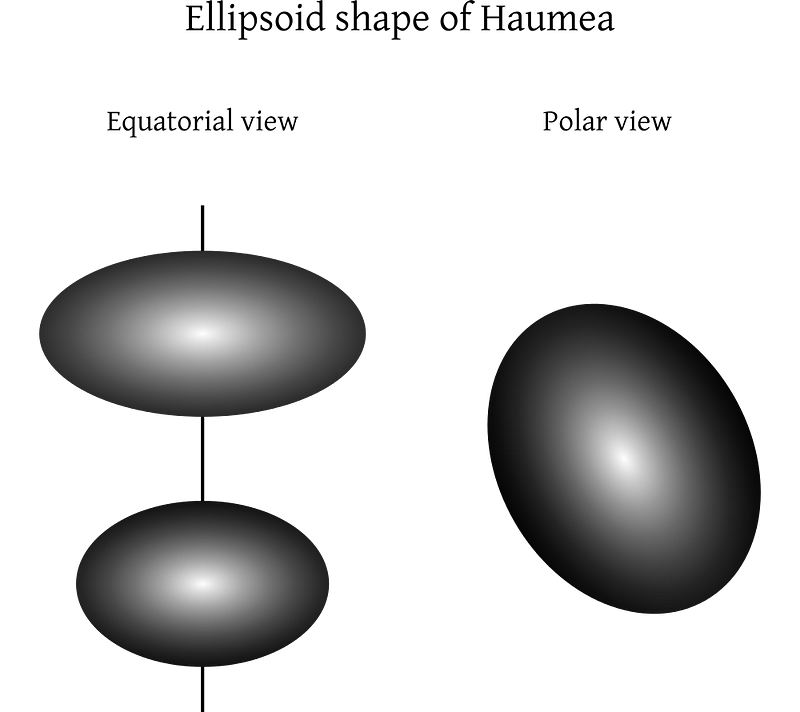
The dwarf planet Haumea, for example, has an equatorial radius that’s estimated to be double its polar radius, thanks to its incredibly rapid rotation. Since the poles are closer to the center of the planet — and hence, closer to the center of planet’s dense mass — the gravitational force is stronger there, and weaker at the equator. Although it’s less pronounced on Earth, the same thing happens here.
On Earth, the gravitational acceleration at the North Pole is slightly above average at 9.83 m/s^2, while at the equator, it’s “only” 9.79 m/s^2. Not a huge difference, but a measurable one: enough to throw off a pendulum clock by over an hour over the course of a month!
2.) The Earth is acted upon by other gravitational bodies. Tidal forces aren’t just for the oceans. Sure, our liquid oceans — with indeterminate shapes but fixed volumes — are much easier to push, pull and deform than the solid rock of the Earth, but tidal forces affect the shape of our planet’s crust as well. It isn’t a large difference, but these forces exist. On worlds like Io — Jupiter’s closest, giant moon — the tidal forces are so great that the world’s crust is routinely torn apart, flooded with lava, and resurfaced, like a great cosmic zamboni.

It’s the reason why, of all the moons in our Solar System, Io is the only one that doesn’t show any impact craters on its surface. Here on Earth, it’s really only the Moon and the Sun that affect the shape of the Earth. Even though these effects are small, they’re measurable, and contribute the same way the Earth’s rotation contributes: by moving us either closer or farther from the Earth’s center, and hence changing our gravitational acceleration.
3.) The Earth has interesting geological features. What counts as interesting? Things like mountains and valleys, which change our distance from the center of the Earth. Remember how Newton’s law of universal gravitation works: the force between any two objects (and hence the acceleration, since F = ma) gets weaker as the square of the distance between them. Add something like 1% to the distance, and the force between these objects drops by approximately 2%. (You can work it out for yourself if you don’t believe me.)
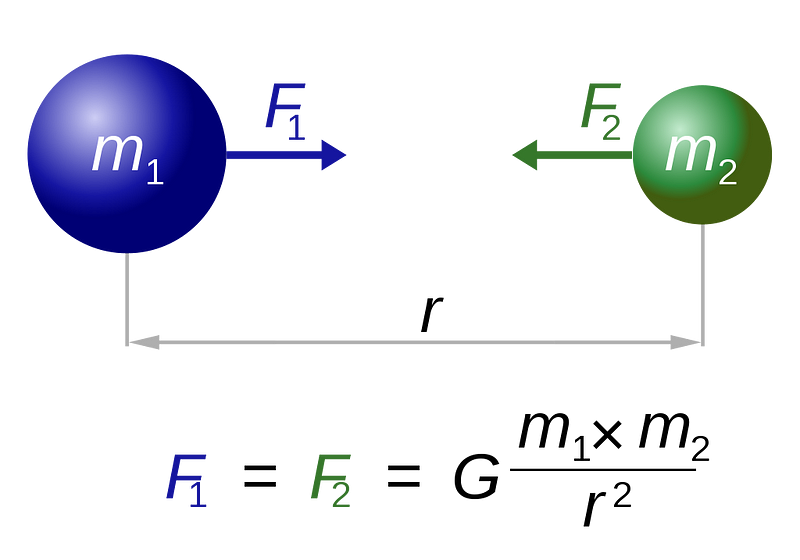
So when you’re on top of a giant mountain, you’re farther away from the Earth’s center than when you’re at sea level. When you’re at the bottom of the ocean, you’re closer to Earth’s center than when you’re at sea level.
And that might make you think about something else: that different layers of the Earth have different densities. If you’re on top of a mountain, you’ve got the whole mass-of-the-mountain beneath your feet, and surely that’s going to contribute to your gravitational acceleration, right? If you’re on the surface of the ocean, you’ve got the whole ocean beneath you. And even if you’re flying through the air, all the mass of the air beneath you is going to pull you down towards the center of the Earth as well. So what we can do is fly satellites above the surface of the Earth and map its surface gravity, measuring the gravitational pull as we orbit over absolutely every point.
What we find is mostly unsurprising: the places where the Earth’s elevation is lowest (closest to the Earth’s center) experience the greatest gravitational acceleration, and the places where the Earth’s elevation is highest (farthest from the planet’s center) experience the smallest acceleration. You’d expect this, because the Earth’s density sharply increases as you go towards the center.
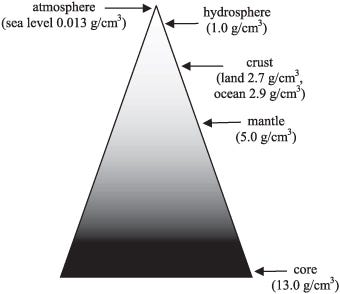
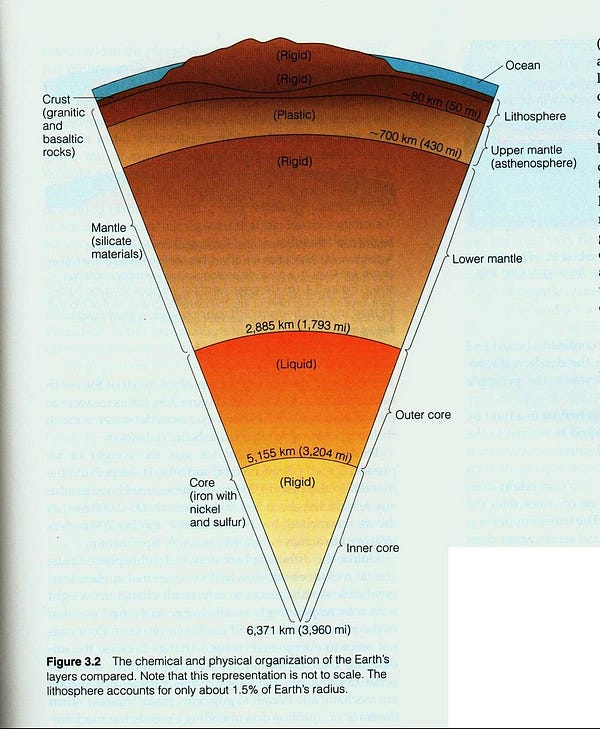
While the rocks that make up mountains — the rocks of the Earth’s crust — come in at a density of around 2.7 g/cm^3, or a little less than three times the density of water, the overall density of Earth is double that. If you go all the way down to the inner core, the density is expected to be more like five times what it is at the surface.
But if you take all of that into account: the structure of the Earth’s insides, the mountains we see, the oceans, the atmosphere, etc., something doesn’t add up. You see, if you actually do the math, and measure the gravity atop the mountains and at the bottom of the oceans, you find something strange: there’s far less mass than you’d expect in the mountains! Which brings up the last, most unexpected point.
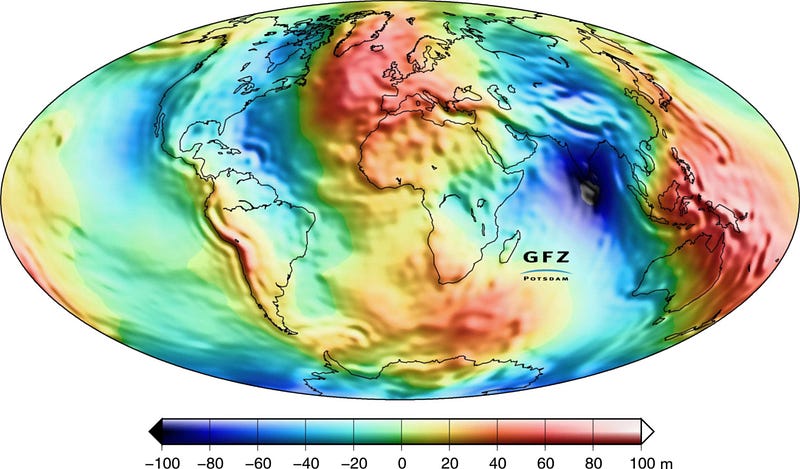
4.) The Earth’s crust “floats” atop the mantle, and mountains work like floating icebergs: there’s far more crust underneath the mountains than there is in the oceans! Need to account for the atmosphere, or the atmosphere that gets displaced by oceans or mountains? That’s the Free-air correction. Need to account for the fact that there’s “extra mountain” (or any land mass) above sea level? That’s the Bouguer correction.
But what about the fact that the crust is low in density? If you want a mountain sticking up, high above sea level, you’ve got to remember that the crust is atop the mantle, which means the thickest crust of the Earth occurs where the highest mountains are, and the thinnest crust is where the deepest ocean trenches are!
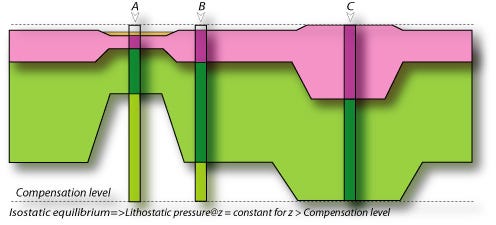
Bizarrely enough, if we wanted to reach the Earth’s mantle, our best bet would be to dive down to the ocean floor and dig there; we’d “only” have to go through maybe 3 km of crust, as opposed to upwards of 25 km atop the Himalayas. This concept is known as isostatic compensation, and was actually uncovered by the famed British astronomer George Airy.
So quite counterintuitively, if you wanted the least amount of mass beneath your feet, you’d climb up to the peak of the highest mountain.
The greatest part of even the highest mountains we can see are underground, stealing valuable volume of the Earth’s interior away from the mantle. If you want to know why there’s a limit to how high a mountain can get, it’s because there’s a limit to how deep into the mantle the crust can penetrate, before all it can do is start spreading out.
Even for something as simple as Newton’s gravity, when you apply it to a new situation — like the layers of the Earth — it shows us that science is still full of counterintuitive surprises. (For more reading, check out the Washington Post and Jonah Miller on mountains.)
Leave your comments at the Starts With A Bang forum on Scienceblogs!





