The 5 Lessons Everyone Should Learn From Einstein’s Most Famous Equation: E = mc²
It’s perhaps the most famous equation of all, with lessons about reality for every one of us.
If you’ve ever heard of Albert Einstein, chances are you know at least one equation that he himself is famous for deriving: E = mc². This simple equation details a relationship between the energy (E) of a system, its rest mass (m), and a fundamental constant that relates the two, the speed of light squared (c²). Despite the fact that this equation is one of the simplest ones you can write down, what it means is dramatic and profound.
At a fundamental level, there is an equivalence between the mass of an object and the inherent energy stored within it. Mass is only one form of energy among many, such as electrical, thermal, or chemical energy, and therefore energy can be transformed from any of these forms into mass, and vice versa. The profound implications of Einstein’s equations touch us in many ways in our day-to-day lives. Here are the five lessons everyone should learn.

1.) Mass is not conserved. When you think about the things that change versus the things that stay the same in this world, mass is one of those quantities we typically hold constant without thinking about it too much. If you take a block of iron and chop it up into a bunch of iron atoms, you fully expect that the whole equals the sum of its parts. That’s an assumption that’s clearly true, but only if mass is conserved.
In the real world, though, according to Einstein, mass is not conserved at all. If you were to take an iron atom, containing 26 protons, 30 neutrons, and 26 electrons, and were to place it on a scale, you’d find some disturbing facts.
- An iron atom with all of its electrons weighs slightly less than an iron nucleus and its electrons do separately,
- An iron nucleus weighs significantly less than 26 protons and 30 neutrons do separately.
- And if you try and fuse an iron nucleus into a heavier one, it will require you to input more energy than you get out.
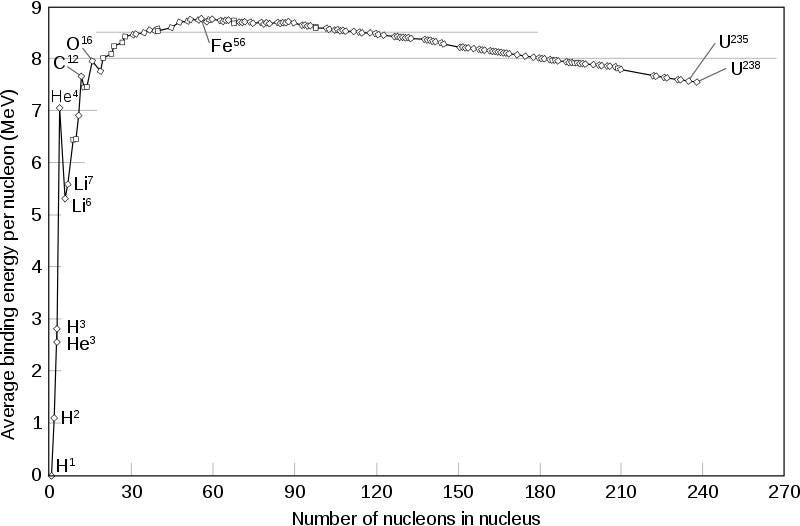
Each one of these facts is true because mass is just another form of energy. When you create something that’s more energetically stable than the raw ingredients that it’s made from, the process of creation must release enough energy to conserve the total amount of energy in the system.
When you bind an electron to an atom or molecule, or allow those electrons to transition to the lowest-energy state, those binding transitions must give off energy, and that energy must come from somewhere: the mass of the combined ingredients. This is even more severe for nuclear transitions than it is for atomic ones, with the former class typically being about 1000 times more energetic than the latter class.
In fact, leveraging the consequences of E = mc² is how we get the second valuable lesson out of it.
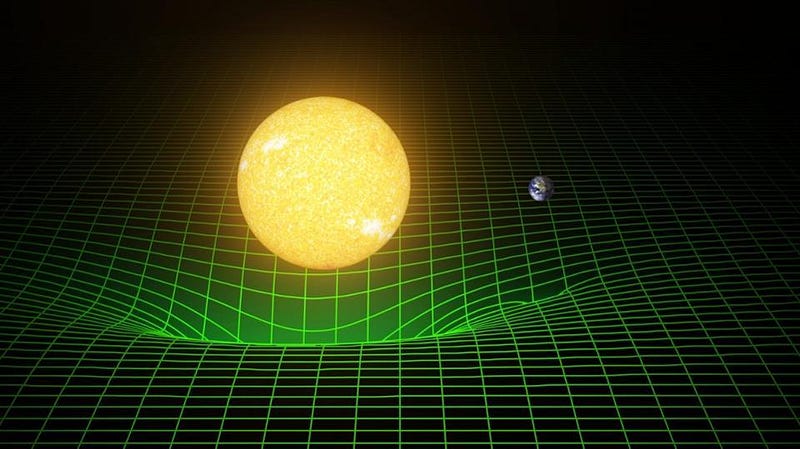
2.) Energy is conserved, but only if you account for changing masses. Imagine the Earth as it orbits the Sun. Our planet orbits quickly: with an average speed of around 30 km/s, the speed required to keep it in a stable, elliptical orbit at an average distance of 150,000,000 km (93 million miles) from the Sun. If you put the Earth and Sun both on a scale, independently and individually, you would find that they weighed more than the Earth-Sun system as it is right now.
When you have any attractive force that binds two objects together — whether that’s the electric force holding an electron in orbit around a nucleus, the nuclear force holding protons and neutrons together, or the gravitational force holding a planet to a star — the whole is less massive than the individual parts. And the more tightly you bind these objects together, the more energy the binding process emits, and the lower the rest mass of the end product.

When you bring a free electron in from a large distance away to bind to a nucleus, it’s a lot like bringing in a free-falling comet from the outer reaches of the Solar System to bind to the Sun: unless it loses energy, it will come in, make a close approach, and slingshot back out again.
However, if there’s some other way for the system to shed energy, things can become more tightly bound. Electrons do bind to nuclei, but only if they emit photons in the process. Comets can enter stable, periodic orbits, but only if another planet steals some of their kinetic energy. And protons and neutrons can bind together in large numbers, producing a much lighter nucleus and emitting high-energy photons (and other particles) in the process. That last scenario is at the heart of perhaps the most valuable and surprising lesson of all.

3.) Einstein’s E = mc² is responsible for why the Sun (like any star) shines. Inside the core of our Sun, where the temperatures rise over a critical temperature of 4,000,000 K (up to nearly four times as large), the nuclear reactions powering our star take place. Protons are fused together under such extreme conditions that they can form a deuteron — a bound state of a proton and neutron — while emitting a positron and a neutrino to conserve energy.
Additional protons and deuterons can then bombard the newly formed particle, fusing these nuclei in a chain reaction until helium-4, with two protons and two neutrons, is created. This process occurs naturally in all main-sequence stars, and is where the Sun gets its energy from.
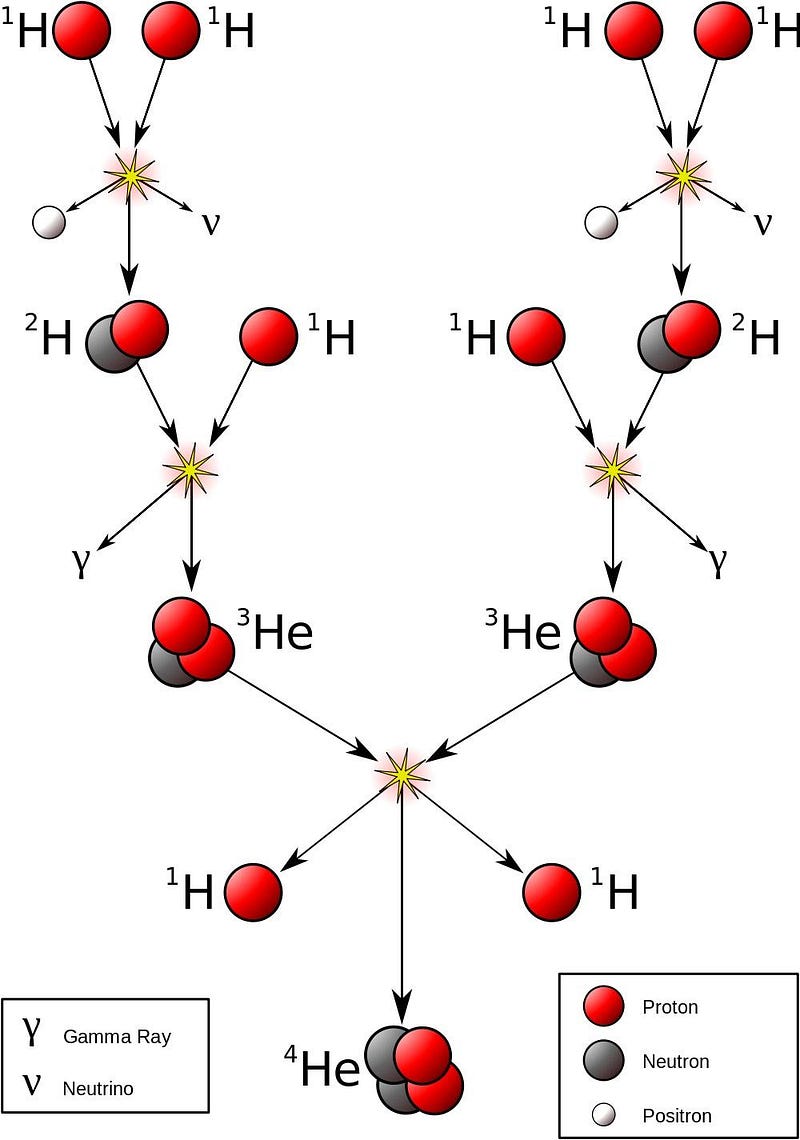
If you were to put this end product of helium-4 on a scale and compare it to the four protons that were used up to create it, you’d find that it was about 0.7% lighter: helium-4 has only 99.3% of the mass of four protons. Even though two of these protons have converted into neutrons, the binding energy is so strong that approximately 28 MeV of energy gets emitted in the process of forming each helium-4 nucleus.
In order to produce the energy we see it produce, the Sun needs to fuse 4 × 10³⁸ protons into helium-4 every second. The result of that fusion is that 596 million tons of helium-4 are produced with each second that passes, while 4 million tons of mass are converted into pure energy via E = mc². Over the lifetime of the entire Sun, it’s lost approximately the mass of the planet Saturn due to the nuclear reactions in its core.

4.) Converting mass into energy is the most energy-efficient process in the Universe. What could be better than 100% efficiency? Absolutely nothing; 100% is the greatest energy gain you could ever hope for out of a reaction.
Well, if you look at the equation E = mc², it tells you that you can convert mass into pure energy, and tells you how much energy you’ll get out. For every 1 kilogram of mass that you convert, you get a whopping 9 × 10¹⁶ joules of energy out: the equivalent of 21 Megatons of TNT. Whenever we experience a radioactive decay, a fission or fusion reaction, or an annihilation event between matter and antimatter, the mass of the reactants is larger than the mass of the products; the difference is how much energy is released.

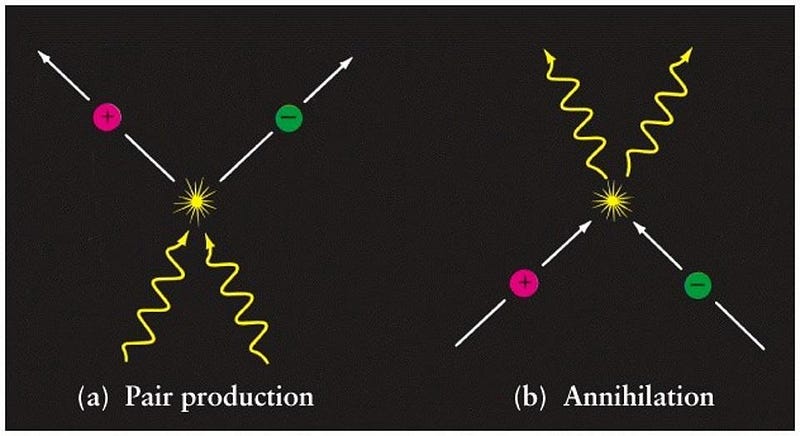
In all cases, the energy that comes out — in all its combined forms — is exactly equal to the energy equivalent of the mass loss between products and reactants. The ultimate example is the case of matter-antimatter annihilation, where a particle and its antiparticle meet and produce two photons of the exact rest energy of the two particles.
Take an electron and a positron and let them annihilate, and you’ll always get two photons of exactly 511 keV of energy out. It’s no coincidence that the rest mass of electrons and positrons are each 511 keV/c²: the same value, just accounting for the conversion of mass into energy by a factor of c². Einstein’s most famous equation teaches us that any particle-antiparticle annihilation has the potential to be the ultimate energy source: a method to convert the entirety of the mass of your fuel into pure, useful energy.
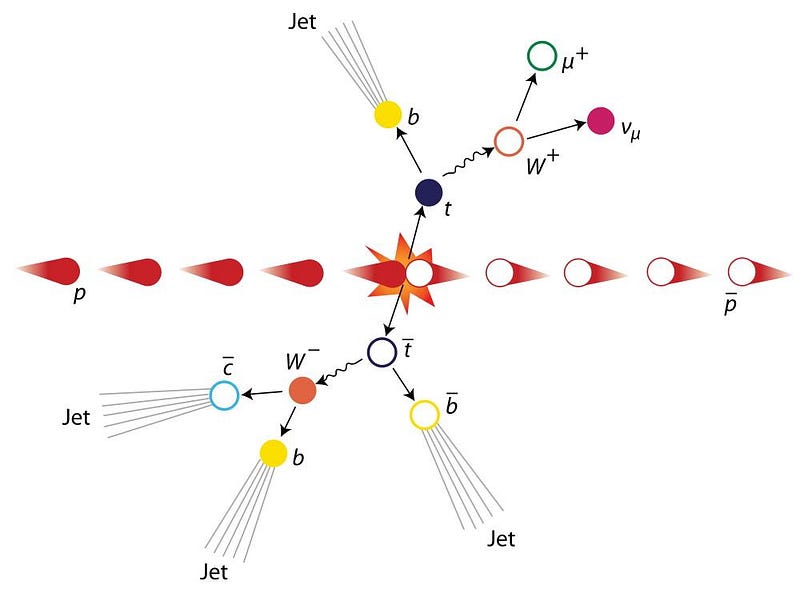
5.) You can use energy to create matter — massive particles — out of nothing but pure energy. This is perhaps the most profound lesson of all. If you took two billiard balls and smashed one into the other, you’d always expect the results to have something in common: they’d always result in two and only two billiard balls.
With particles, though, the story is different. If you take two electrons and smash them together, you’ll get two electrons out, but with enough energy, you might also get a new matter-antimatter pair of particles out, too. In other words, you will have created two new, massive particles where none existed previously: a matter particle (electron, muon, proton, etc.) and an antimatter particle (positron, antimuon, antiproton, etc.).
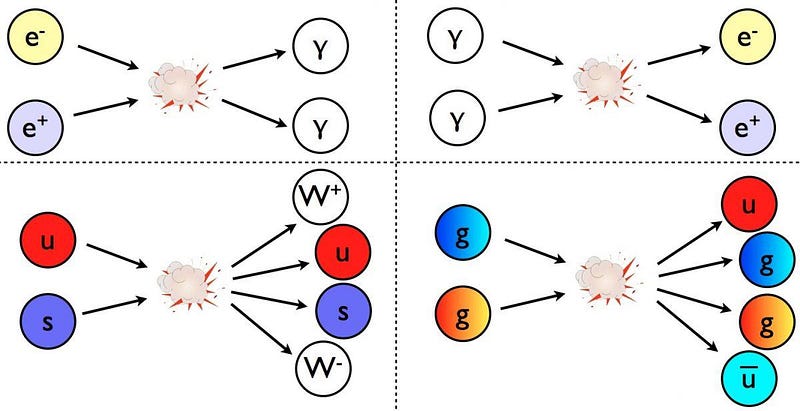
This is how particle accelerators successfully create the new particles they’re searching for: by providing enough energy to create those particles (and, if necessary, their antiparticle counterparts) from a rearrangement of Einstein’s most famous equation. Given enough free energy, you can create any particle(s) with mass m, so long as there’s enough energy to satisfy the requirement that there’s enough available energy to make that particle via m = E/c². If you satisfy all the quantum rules and have enough energy to get there, you have no choice but to create new particles.
Einstein’s E = mc² is a triumph for the simple rules of fundamental physics. Mass isn’t a fundamental quantity, but energy is, and mass is just one possible form of energy. Mass can be converted into energy and back again, and underlies everything from nuclear power to particle accelerators to atoms to the Solar System. So long as the laws of physics are what they are, it couldn’t be any other way. As Einstein himself said:
It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamiliar conception for the average mind.
More than 60 years after Einstein’s death, it’s long past time to bring his famous equation down to Earth. The laws of nature aren’t just for physicists; they’re for every curious person on Earth to experience, appreciate, and enjoy.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





