Surprise! The Hubble Constant Changes Over Time

The rate at which the Universe has expanding has changed tremendously in 13.8 billion years. So why do we call it the Hubble constant?

The Universe is an enormous place, filled with stars and galaxies for billions of light years in all direction. Ever since the Big Bang, light has been traveling from every source that’s created it, with a tiny fraction eventually arriving at our eyes. But the light doesn’t simply propagate through the space between where its emitted and where we are today; the fabric of space itself is expanding.

The farther away a galaxy is, the more the expansion of space stretches — and therefore, redshifts — the light that will eventually arrive at our eyes. As we look to greater and greater distances, we see redshifts that increase. If we plot out how this apparent recession speed scales with distance, we get a nice, straight-line relationship: Hubble’s law. But the slope of that line, known as Hubble’s constant, isn’t actually a constant at all. It’s one of the biggest misconceptions in all of astronomy.

There are two ways that we understand the Universe’s expansion: theoretically and observationally. When we look out at the Universe, we see a number of important facts about the expansion:

• the Universe expands at the same rate in all directions,
• the more distant a galaxy is, the faster it recedes from us,
• and that this is only true on average.

When we look at individual galaxies, there are large discrepancies in the speeds they actually have, and this is due to gravitational interactions of everything else in the entire Universe.

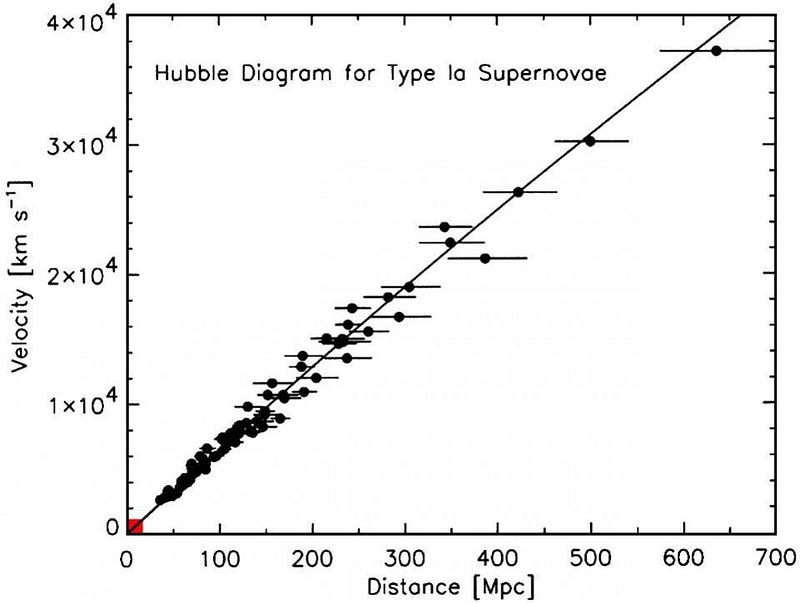
But this is not an insurmountable problem. The Universe is not a place where we only have a few galaxies we can measure the redshift and distance to; there are literally millions of galaxies that we’ve done this for. As we find a huge slew of galaxies, we can do what’s called “binning” them together, where we’ll take galaxies in a certain distance range and average them together, calculating an average redshift for them. As we do this, we find that straight-line relation that defines Hubble’s law.

Here’s the surprise, though. If we look to large enough distances, we can see that the expansion rate no longer follows that straight-line law, but rather curves.

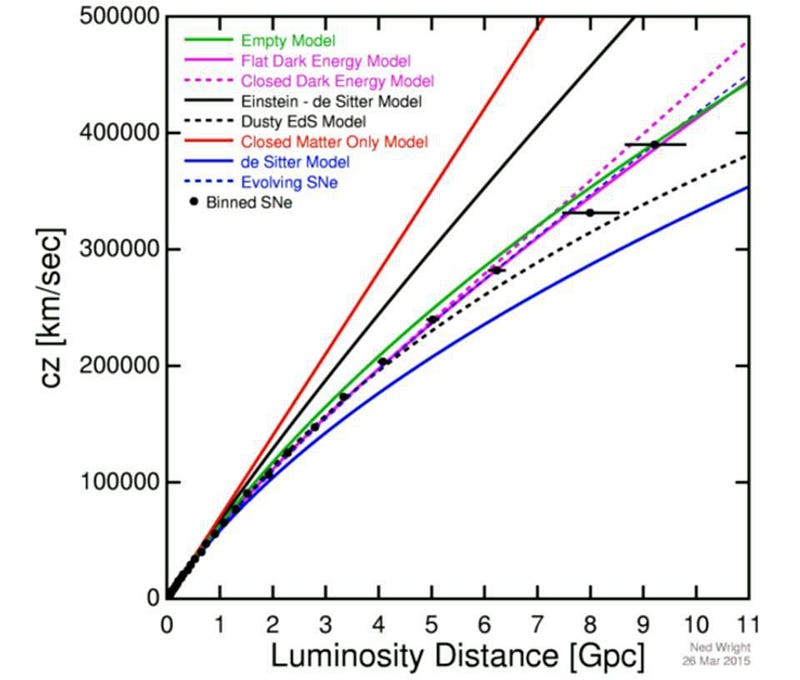
When we use a term like “the Hubble constant,” we’re talking about the slope of that line. If it’s not a line — i.e., if the slope changes — that tells us that the Hubble expansion rate of the Universe isn’t truly a constant after all! The reason we call it the Hubble constant is because the Universe expands at the same rate at every location in the Universe: the Hubble constant is constant throughout space.

But the expansion rate, and therefore the value of the Hubble constant, changes with time. This isn’t a puzzle, but is rather exactly what we expect. To understand this, let’s look at it from the other point of view: theoretically.

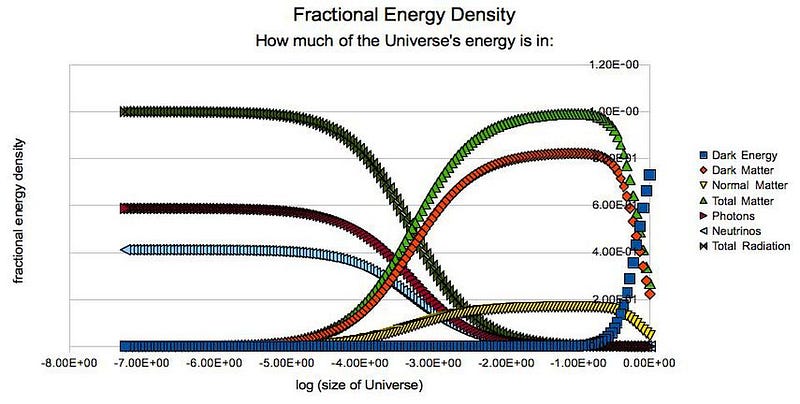
The first Friedmann equation is what you arrive at if you start with a Universe that’s uniformly filled with matter, radiation, and whatever other forms of energy you want. The only assumptions are that the Universe is isotropic (the same in all directions), homogeneous (with the same average density everywhere), and governed by General Relativity. If you assume this, you get a relation between H, the Hubble rate (on the left-hand side), and all the various forms of matter and energy in the Universe (on the right-hand side).

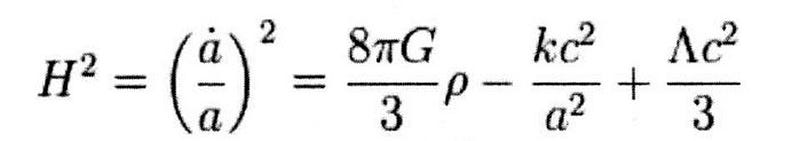
Interestingly, as your Universe expands, the density of matter, radiation, and energy are allowed to change. For example, as your Universe expands, its volume increases, but the total number of particles within your Universe stays the same. This means that, in an expanding Universe, for:

• matter, its density drops as a^-3,
• radiation, its density drops as a^-4,
• and for dark energy, its density remains constant, evolving as a⁰,

where a is the scale factor (a proxy for the distance or the radius) of the Universe. As time goes on, a grows, and therefore different components of the Universe become more-or-less important relative to one another.

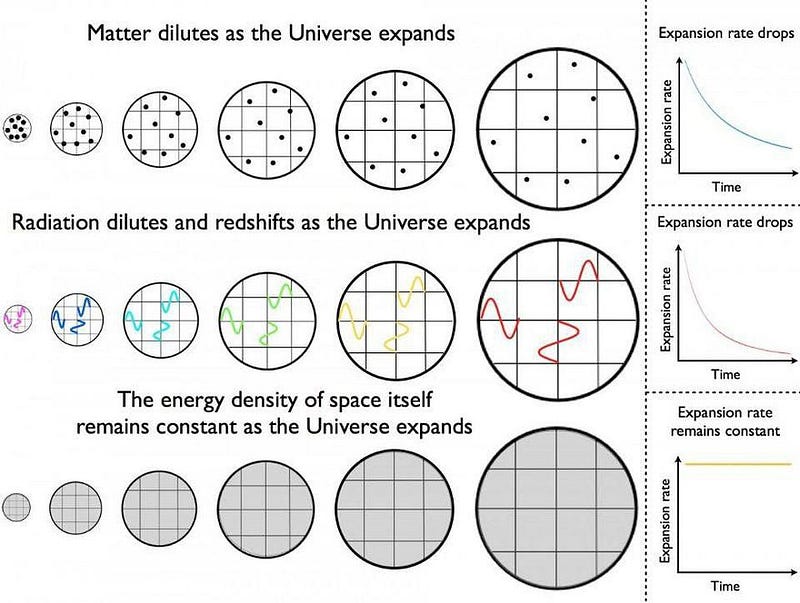
A Universe with a greater overall energy density has a greater expansion rate. On the contrary, one with a smaller energy density has a lower expansion rate. As the Universe ages, it expands; as it expands, the matter and radiation within it becomes less dense; as it becomes less dense, the expansion rate drops. The expansion rate, at any given time, determines the value of the Hubble constant. In the distant past, the expansion rate was much larger, while today it’s the smallest it’s ever been.

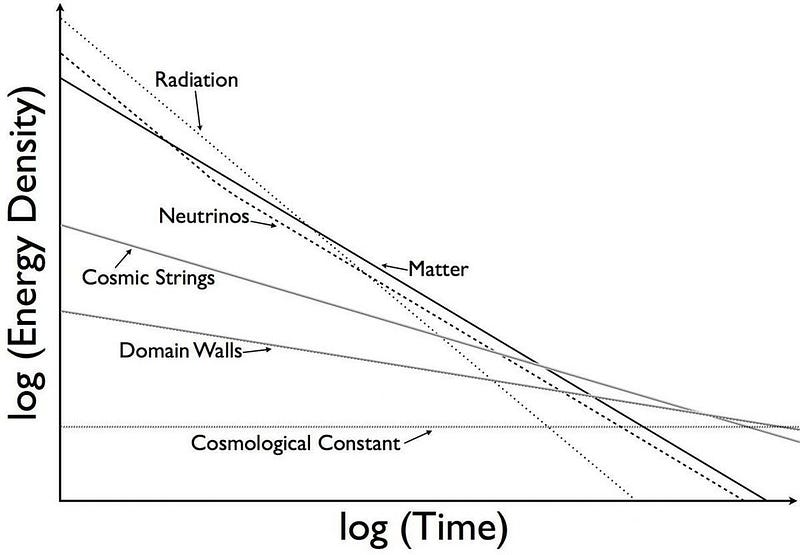
So why, then, you might wonder, do the very distant galaxies we observe appear to follow this straight-line relation? It’s because all of the light that arrives at our eyes, from the light that was emitted by a galaxy next door to the light that was emitted from a galaxy billions of light years away, is all 13.8 billion years old by time it reaches us. The age of everything in the Universe, by time it reaches us today, has lived through the same ever-changing Universe that we have. The Hubble constant was higher in the distant past, when much of the light was emitted, but it’s taken billions of years for that light to arrive at our eyes.

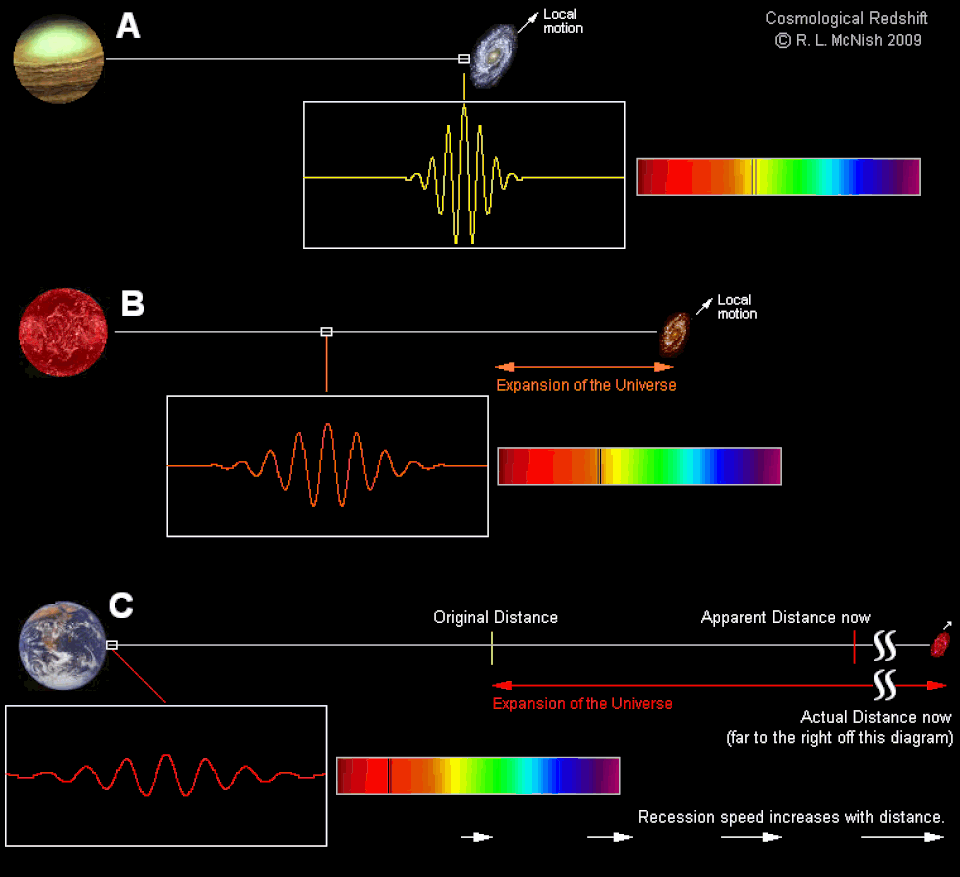
Over that time, the Universe has expanded, meaning that the wavelength of that light has stretched. Only over the past 6 billion years or so has dark energy become important, and we’ve now reached the time where it’s fast becoming the only component of the Universe that has an impact on our expansion rate. If we went back to a time when the Universe was half its present age, the expansion rate was 80% greater than it is today. When the Universe was just 10% of its current age, the expansion rate was 17 times greater than its present value.

But when the Universe reaches 10 times its current age, the expansion rate will only be 18% smaller than it is today.

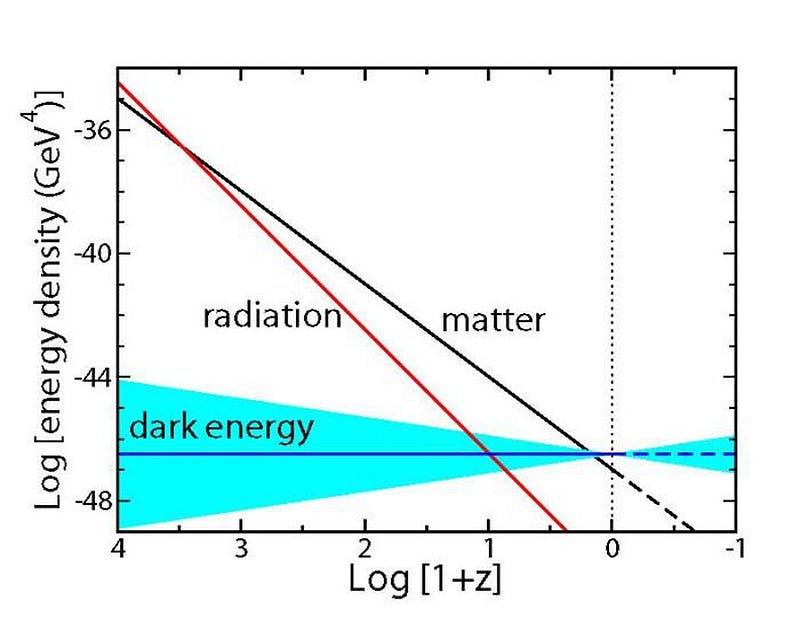
This is due to the presence of dark energy, which behaves as a cosmological constant. In the far future, matter and radiation will both become relatively unimportant compared to dark energy, meaning that the Universe’s energy density will remain constant. Under these circumstances, the expansion rate will reach a steady, finite value and stay there. As we move into the far future, the Hubble constant will become a constant not only in space, but in time as well.

In the far future, by measuring the velocity and distance to all the objects we can see, we’d get the same slope for that line everywhere. The Hubble constant will truly become a constant.

If astronomers were more careful about their words, they would have called H the Hubble parameter, rather than the Hubble constant, since it changes over time. But for generations, the only distances we could measure were close enough that Happeared to be constant, and we’ve never updated this. Instead, we have to be careful to note that H is a function of time, and only today — where we call it H_0 — is it a constant. In reality, the Hubble parameter changes over time, and it’s only a constant everywhere in space. Yet if we lived far enough in the future, we’d see that H stops changing entirely. As careful as we can be to make the distinction between what’s actually constant and what changes now, in the far future, dark energy ensures there will be no difference at all.