Standard Model survives its biggest challenge yet

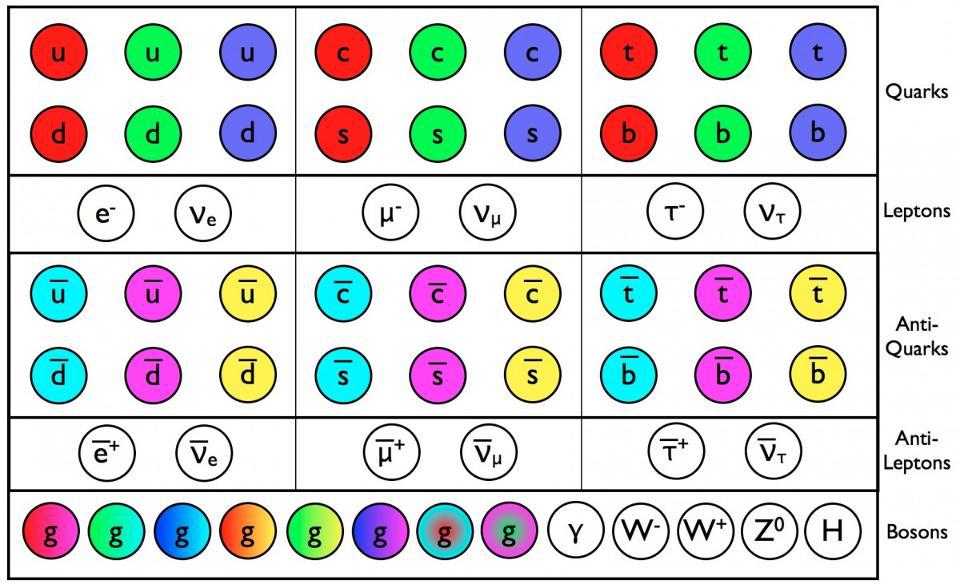
- With the Standard Model of particle physics, we don’t simply get the particles that make up our conventional existence, but three copies of them: multiple generations of quarks and leptons.
- According to the Standard Model, many processes that occur in one generation of leptons (electrons, muons, and taus) should occur in all the others, so long as you account for their mass differences.
- This property, known as lepton universality, was challenged by three independent experiments. But in a tour-de-force advance, LHCb has vindicated the Standard Model once again. Here’s what it means.
In all of science, perhaps the greatest quest of all is to go beyond our current understanding of how the Universe works to find a more fundamental, truer description of reality than what we have at present. In terms of what the Universe is made of, this has happened many times, as we discovered:
- the periodic table of the elements,
- the fact that atoms have electrons and a nucleus,
- that the nucleus contains protons and neutrons,
- that protons and neutrons themselves are composite particles made of quarks and gluons,
- and that there are additional particles beyond quarks, gluons, electrons, and photons that compose our reality.
The full description of particles and interactions known to exist comes to us in the form of the modern Standard Model, which has three generations of quarks and leptons, plus the bosons that describe the fundamental forces as well as the Higgs boson, responsible for the non-zero rest masses of all the Standard Model particles.
But very few people believe that the Standard Model is complete, or that it won’t be superseded someday by a more comprehensive, fundamental theory. One of the ways we’re attempting to do that is by testing the Standard Model’s predictions directly: by creating heavy, unstable particles, watching them decay, and comparing what we observe to the Standard Model’s predictions. For more than a decade, the idea of lepton universality seemed incompatible with what we were observing, but a superior test by the LHCb collaboration just gave the Standard Model a stunning victory. Here’s the full, triumphant story.
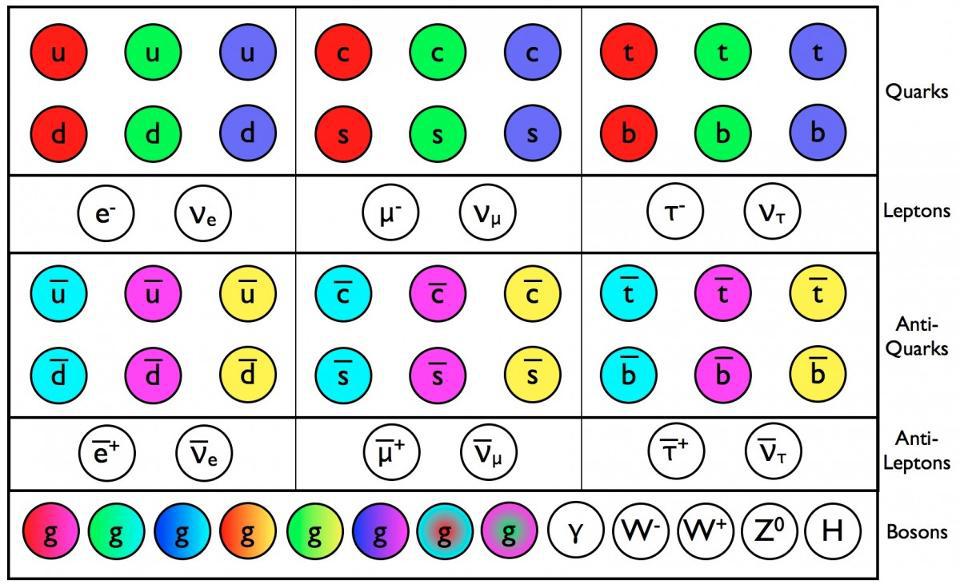
The Standard Model is so powerful because it basically combines three theories — the theory of the electromagnetic force, the weak force, and the strong force — into one coherent framework. All of the particles that exist can have charges under any or all of these forces, interacting directly with the bosons that mediate the interactions corresponding to that particular charge. The particles that make up the matter we know of are generally called fermions, and consist of the quarks and leptons, which come in three generations apiece as well as their own antiparticles.
One of the ways we have of testing the Standard Model is by looking at its predictions in detail, calculating what the probability would be of all of the possible outcomes for any particular setup. For example, whenever you create an unstable particle — e.g., a composite particle like a meson or baryon made up of one or more heavy quarks, like a strange, charm, or bottom quark — there isn’t just one decay path it can take, but a wide variety, all with their own explicit probability of occurring. If you can calculate the probability of all possible outcomes and then compare what you measure at a particle accelerator that produces them in great numbers, you can put the Standard Model to a myriad of tests.
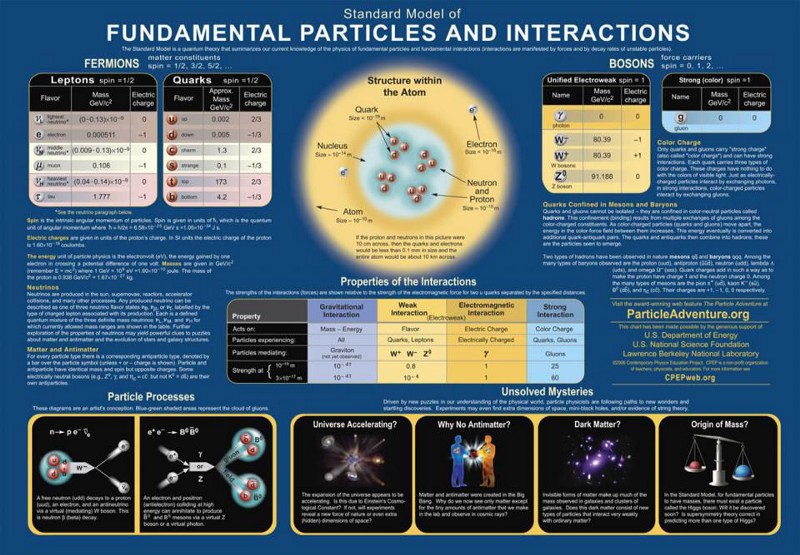
One type of test we can perform is called lepton universality: the notion that, except for the fact that they have different masses, the charged leptons (electron, muon, tau) and the neutrinos (electron neutrino, muon neutrino, tau neutrino), as well as their respective antiparticles, should all behave the same as one another. For example, when a very massive Z-boson decays — and take note that the Z-boson is much more massive than all of the leptons — it has equal probabilities of decaying into an electron-positron pair as it does into a muon-antimuon or a tau-antitau pair. Similarly, it has equal probability of decaying into neutrino-antineutrino pairs of all three flavors. Here, experiment and theory agree, and the Standard Model is safe.
But over the first part of the 21st century, we started to see some evidence that when both charged and neutral mesons that contain bottom quarks decayed into a meson that contained a strange quark as well as a charged lepton-antilepton pair, the probability of getting an electron-positron pair differed from the probability of getting a muon-antimuon pair by much more than their mass differences could account for. This hint, from experimental particle physics, led many to hope that perhaps we had stumbled upon a violation of the Standard Model’s predictions, and hence, a hint that could take us beyond known physics.
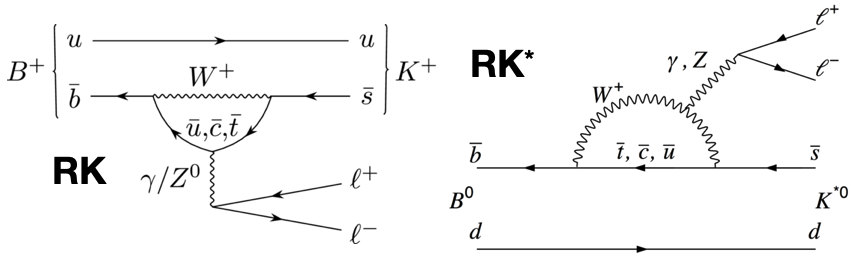
Starting in 2004, two experiments that were producing significant numbers of both charged and neutral mesons that contained bottom quarks, BaBar and Belle, sought to put the notion of lepton universality to the test. If the probabilities, when corrected for what we call the “square of the dilepton invariant mass” (i.e., the energy taken to produce either an electron-positron or muon-antimuon pair), or q², corresponded to the Standard Model’s predictions, then the ratio between the number of electron-positron and muon-antimuon decay events should be 1:1. That was what was expected.
Belle’s results were completely consistent with a 1:1 ratio, but Babar’s were a little bit low (just under 0.8), which got a lot of people excited about the Large Hadron Collider at CERN. You see, in addition to the two main detectors — ATLAS and CMS — there was also the LHCb detector, optimized and specialized to look for decaying particles that were created with a bottom quark inside. Three results were published as more and more data came in from LHCb testing lepton universality, with that ratio stubbornly remaining low relative to 1. Going into the latest results, the error bars kept shrinking with more statistics, but the average ratio hadn’t changed substantially. Many began to get excited as the significance increased; perhaps this would be the anomaly that at last “broke” the Standard Model for good!
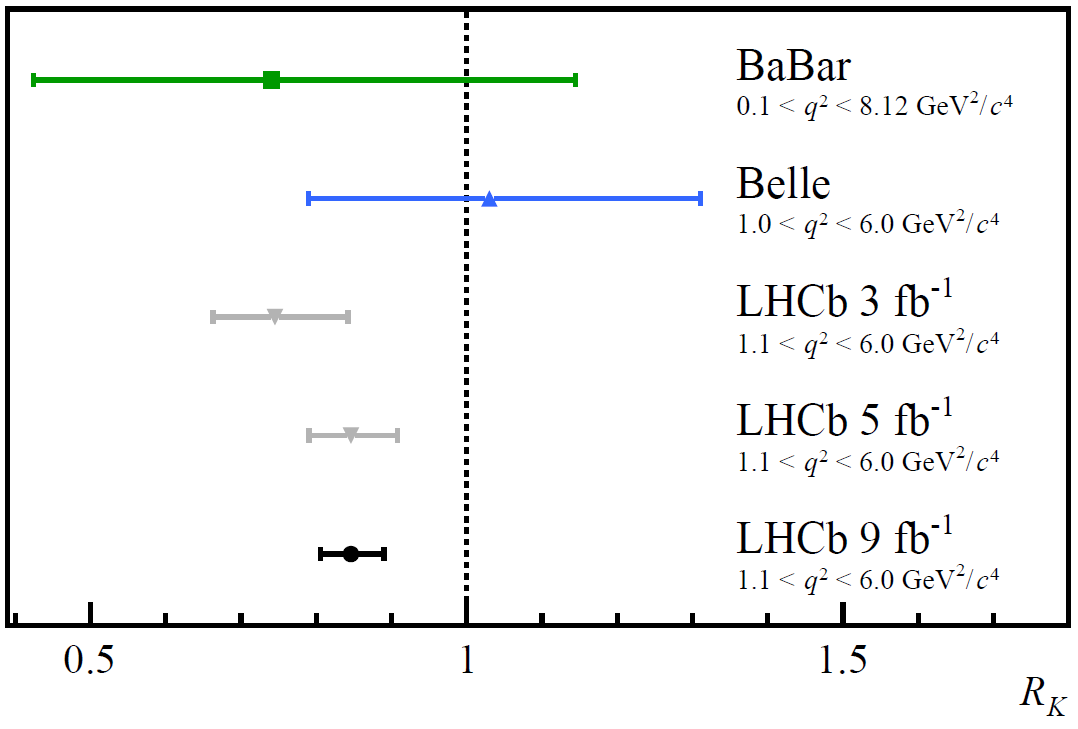
It turns out there were actually four independent tests that could be done with the LHCb data:
- to test the decay of charged B-mesons into charged kaons for low q² parameters,
- to test the decay of charged B-mesons into charged kaons for higher q² parameters,
- to test the decay of neutral B-mesons into excited-state kaons for low q² parameters,
- and to test the decay of neutral B-mesons into excited-state kaons for higher q² parameters.
If there were new physics that existed that could come into play and affect these Standard Model predictions, you’d expect them to play a greater role for higher values of q² (or, in other words, at higher energies), but you’d expect them to better agree with the Standard Model for lower values of q².
But that wasn’t what the data was indicating. The data was showing that all of the tests that had been conducted (which were three of the four; all but the charged B-mesons at low q²) were indicating the same low value of that ratio that should’ve been 1:1. When you combined the results of all tests conducted, the result was indicating a ratio of about 0.85, not 1.0, and it was significant enough that there was only about a 1-in-1000 chance that it was a statistical fluke. That left three main possibilities, all of which needed to be considered.
- This really was a statistical fluke, and that with more and better data, the ratio of electron-positrons to muon-antimuons should regress to the expected 1.0 value.
- There was something funny going on with how we were either collecting or analyzing the data — a systematic error — that had slipped through the cracks.
- Or the Standard Model really is broken, and that with better statistics, we’d reach the 5- threshold to announce a robust discovery; the prior results were suggestive, at about a 3.2- significance, but not there yet.
Now, there’s really no good “test” to see if option 1 is the case; you simply need more data. Similarly, you can’t tell if option 3 is the case or not until you reach that vaunted threshold; until you get there, you’re only speculating.
But there are lots of possible options for how option 2 could rear its head, and the best explanation I know of is to teach you about a word that has a special meaning in experimental particle physics: cuts. Whenever you have a particle collider, you have a lot of events: lots of collisions, and lots of debris that comes out. Ideally, what you’d do is keep 100% of the interesting, relevant data that’s important for the particular experiment you’re trying to perform, while throwing away 100% of the irrelevant data. That’s what you’d analyze to arrive at your results and to inform your conclusions.
But it’s not actually possible, in the real world, to keep everything you want and throw away everything you don’t. In a real particle physics experiment, you look for specific signals in your detector in order to identify the particles you’re looking for: tracks that curve a certain way within a magnetic field, decays that display a displaced vertex a certain distance from the collision point, specific combinations of energy and momentum that arrive in the detector together, etc. When you make a cut, you make it based on a measurable parameter: throwing away what “looks like” what you don’t want and keeping what “looks like” what you do.
Only then, once the proper cut is made, do you do your analysis.
Upon learning this for the first time, many experimental particle physics undergrad and graduate students have a miniature version of an existential crisis. “Wait, if I make my cuts in a particular way, couldn’t I just wind up ‘discovering’ anything I wanted to at all?” Thankfully, it turns out there are responsible practices that one must follow, including understanding both your detector’s efficiency as well as what other experimental signals might overlap with what you’re attempting to separate out by making your cuts.
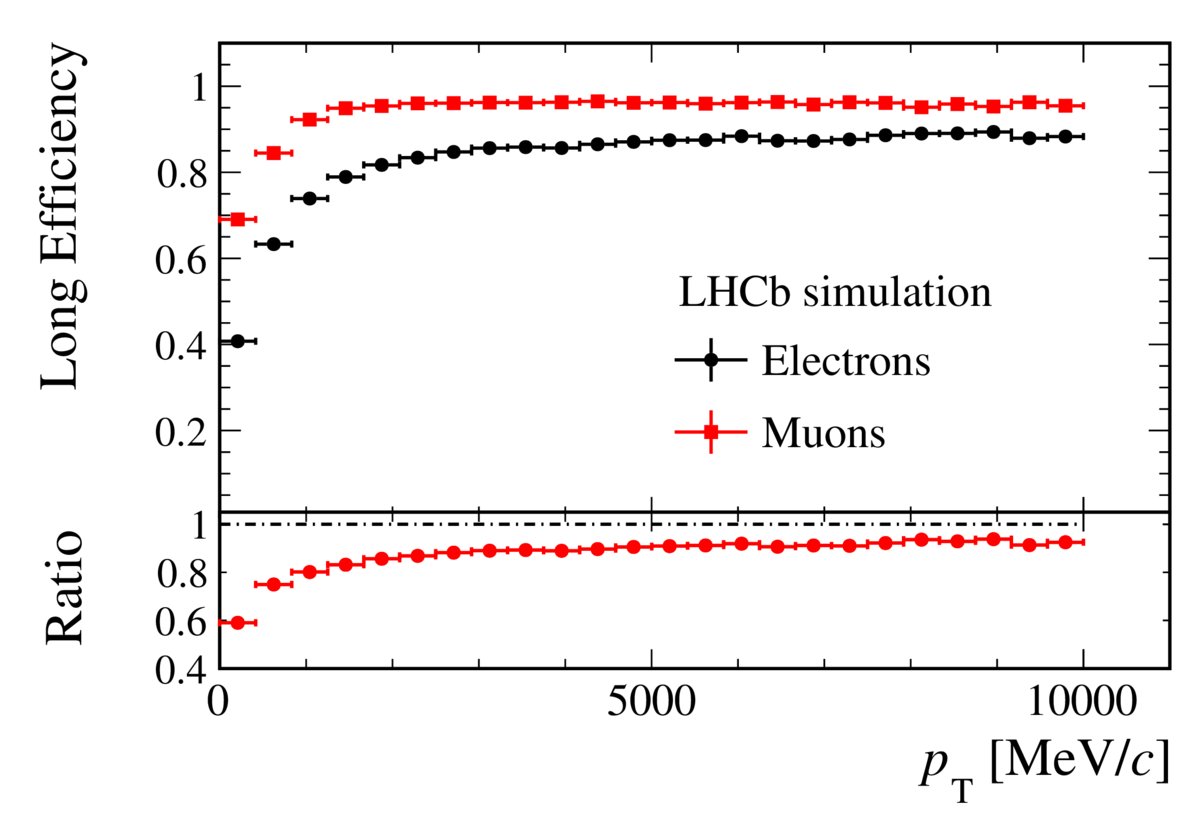
It had been known for some time that electrons (and positrons) have different efficiencies in the LHCb detector than muons (and antimuons), and that effect was well-accounted for. But sometimes, when you have a particular type of meson traveling through your detector — a pion or a kaon, for instance — the signal that it creates is very similar to the signals that electrons generate, and so misidentification is possible. This is important, because if you’re trying to measure a very specific process that involves electrons (and positrons) as compared to muons (and antimuons), then any confounding factor can bias your results!
This is precisely the type of “systematic error” that can pop up and make you think you’re detecting a significant departure from the Standard Model. It’s a dangerous type of error, because as you gather greater and greater statistics, the departure you infer from the Standard Model will become more and more significant. And yet, it isn’t a real signal that indicates that something about the Standard Model is wrong; it’s simply a different type of decay that can bias you in either direction, as you’re attempting to see decays with both kaons and electron-positron pairs. If you either oversubtract or undersubstract the unwanted signal, you’re going to wind up with a signal that fools you into thinking you’ve broken the Standard Model.
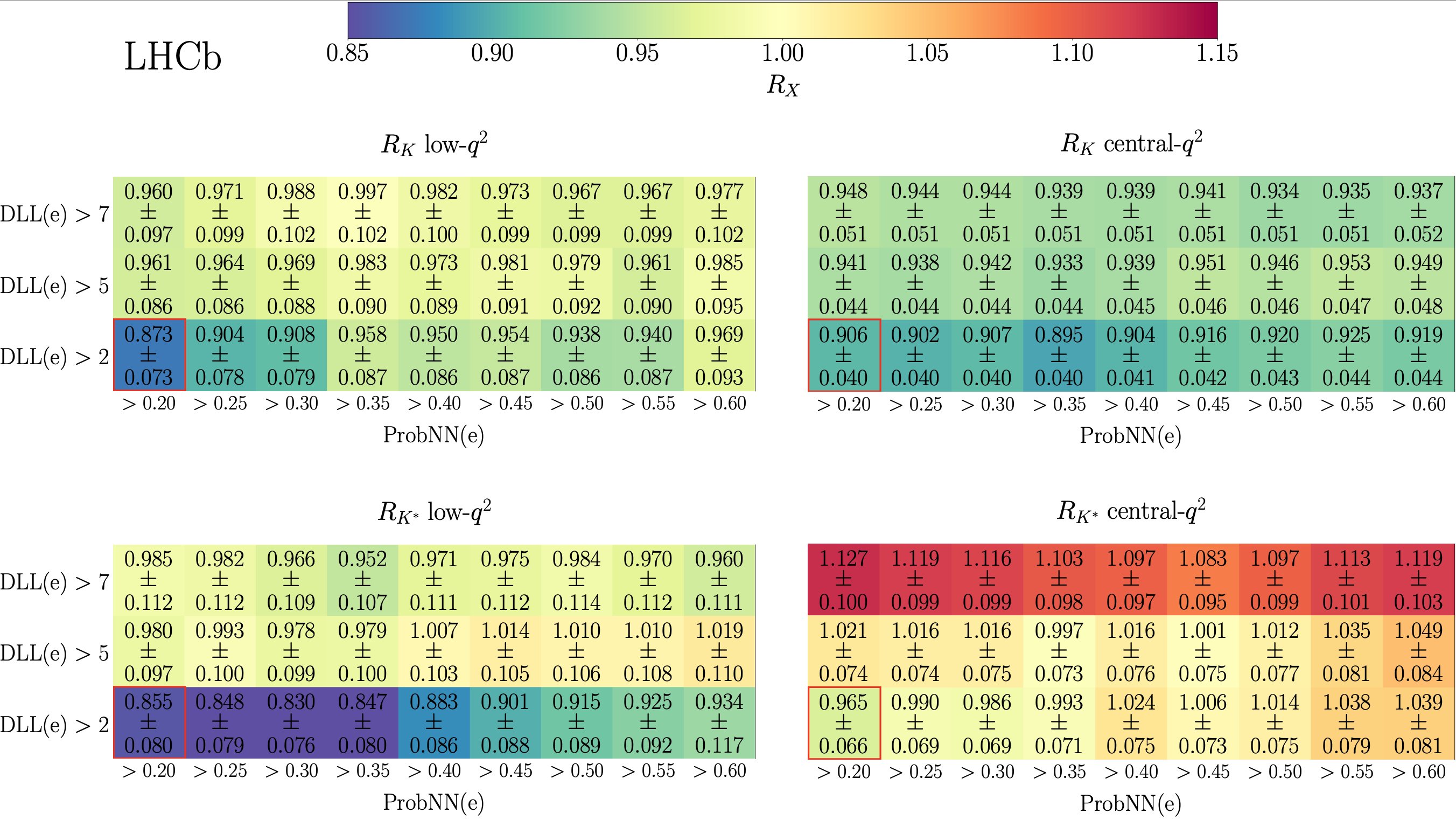
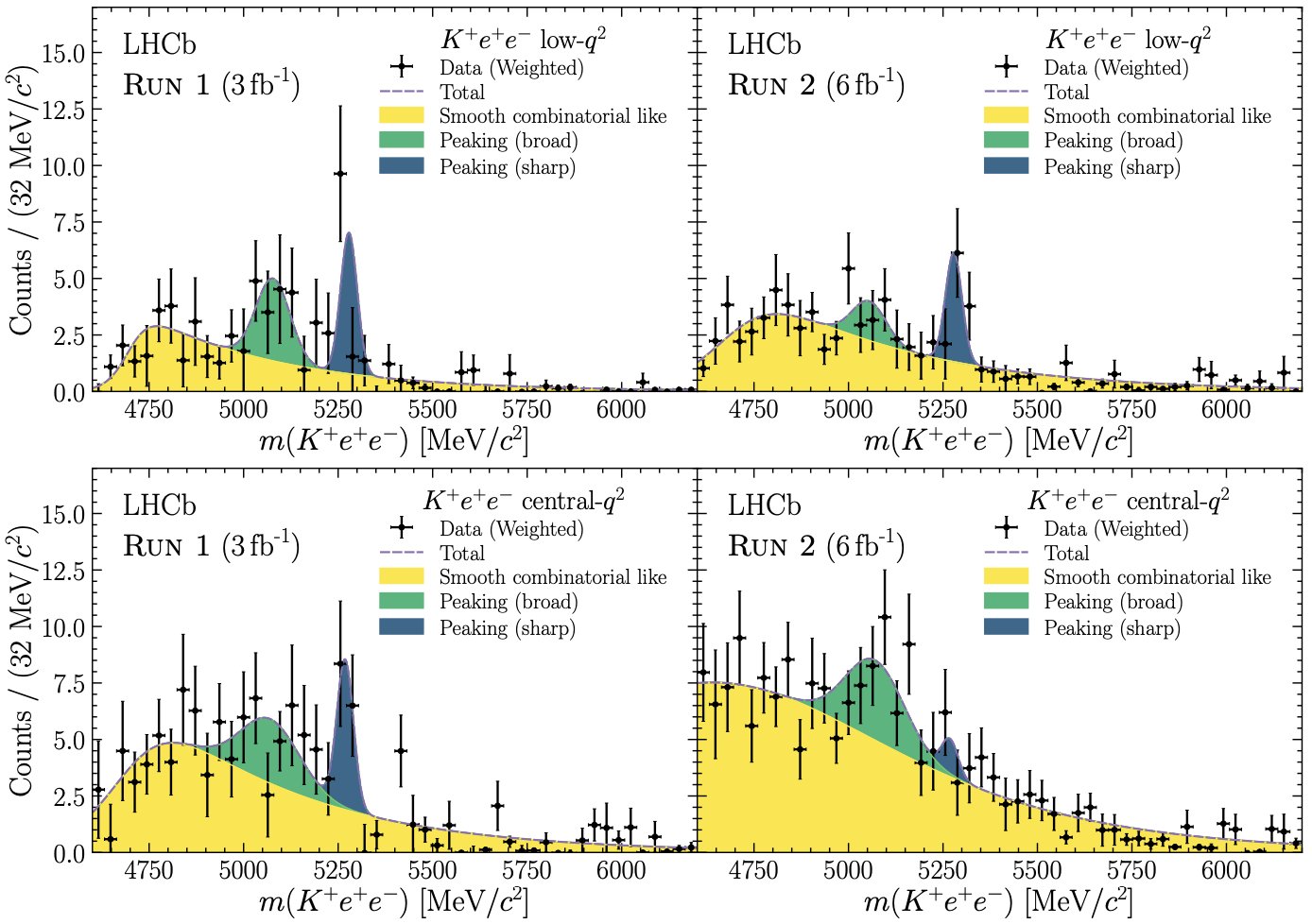
The chart, above, shows how these misidentified backgrounds were discovered. These four separate classes of measurements show that the inferred probabilities of having one of these kaon-electron-positron decays from a B-meson all change together when you change the criteria to answer the key question of, “Which particle in the detector is an electron?” Because the results changed coherently, the LHCb scientists — after a herculean effort — were finally able to better identify the events that revealed the desired signal from previously-misidentified background events.
With this recalibration now possible, the data was able to be analyzed correctly in all four channels. Two things of note could immediately be observed. First, the ratio of the two types of leptons that could be produced, electron-positron pairs and muon-antimuon pairs, all shifted dramatically. Instead of about 0.85, the four ratios all leapt up to become very close to 1.0, with the four respective channels showing ratios of 0.994, 0.949, 0.927, and 1.027 each. But second off, the systematic errors, aided by the better understanding of background, shrank so that they’re only between 2 and 3% in each channel, a remarkable improvement.
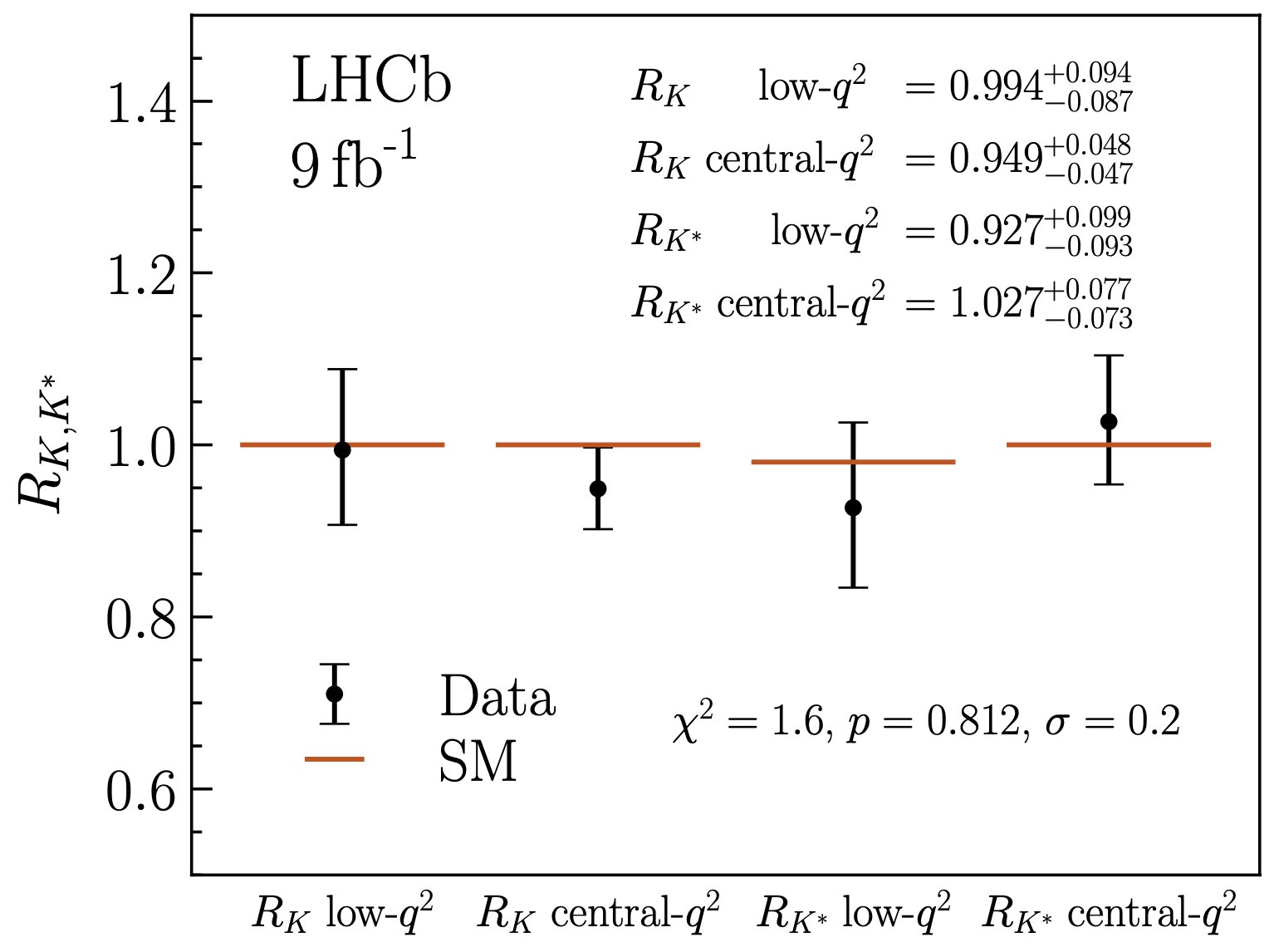
All told, this now means that lepton universality — a core prediction of the Standard Model — now appears to hold true across all the data we have, something that couldn’t be said before this reanalysis. It means that what appeared to be a ~15% effect has now evaporated, but it also means that future LHCb work should be able to test lepton universality to the 2-3% level, which would be the most stringent test of all time on this front. Finally, it further validates the value and capabilities of experimental particle physics and the particle physicists who conduct it. Never has the Standard Model been tested so well.
The importance of testing your theory in novel ways, to better precision and with larger data sets than ever before, cannot be overstated. Sure, as theorists, we are always searching for novel ways to go beyond the Standard Model that remain consistent with the data, and it’s exciting whenever you discover a possibility that’s still viable. But physics, fundamentally, is an experimental science, driven forward by new measurements and observations that take us into new, uncharted territory. As long as we keep pushing the frontiers forward, we’re guaranteed to someday discover something novel that unlocks whatever the “next level” is in refining our best approximation of reality. But if we allow ourselves to be mentally defeated before exhausting every avenue available to us, we’ll never learn how truly rich the ultimate secrets of nature actually are.
The author thanks repeated correspondence with Patrick Koppenburg and a wonderfully informative thread by a pseudonymous LHCb collaboration member.