Why the cosmic speed limit is below the speed of light
- All particles with a non-zero mass are limited, by the laws of relativity, to remaining below the speed of light.
- However, there’s an even stricter speed limit, and an energy limit, set by other particles in the Universe, like the cosmic microwave background radiation.
- This limit, known as the GZK cutoff, ensures that the cosmic speed limit for particles is even lower than the speed of light itself.
If you want to travel as fast as you can through the Universe, your best bet is to pump as much energy as possible into as small a mass as you can find. As you add progressively more kinetic energy and momentum to your particle, it will travel through space more quickly, approaching the ultimate cosmic speed limit: the speed of light. No matter how much energy you manage to add into the particle in question, you can only get it to approach the speed of light — it will never reach it. Since the total amount of energy in the Universe is finite, but the energy required for a massive particle to reach the speed of light is infinite, it can never get there.
But in our real-life Universe — not the idealized “toy” version we play with in our heads — we don’t simply have arbitrary amounts of energy to give to particles, and we also have to accept that they’re traveling through the space that actually exists, rather than what we imagine as a complete, perfect vacuum. While the Universe is capable of imparting far more energy to particles through natural accelerators — like neutron stars and black holes — than we can ever give them on Earth, even at state-of-the-art machines like CERN’s Large Hadron Collider, the fact that “the vacuum of space” isn’t a perfect vacuum is far more limiting than we often care to admit. Rather than the speed of light, the actual speed limit of particles is below that: set by what we call the GZK cutoff. Here’s what truly limits our motion through space.
Credit: NASA/Sonoma State University/Aurore Simmonet
There are two facts that, when taken together, teach us that reality is not as simple as Newton intuited. Those facts are:
- The particles that rapidly travel through the Universe are largely protons, electrons, heavier atomic nuclei, and occasionally positrons or anti-protons. All of these particles, detectable here on Earth and in space as cosmic rays, are electrically charged.
- Light, which exists from many different sources, including stars, galaxies, and even the Big Bang itself, is an electromagnetic wave, and can easily interact with charged particles.
While even today’s modern physicists often automatically default to Newtonian-like thinking, we have to be careful to think of things as mere masses moving through the Universe, accelerated only by the forces that other particles and fields exert on them. Instead, we have to remember that the Universe is composed of physical quanta: individual energy packets with properties of both wave and particle, and that those quanta, unless somehow specifically forbidden from doing so, will always interact with one another.

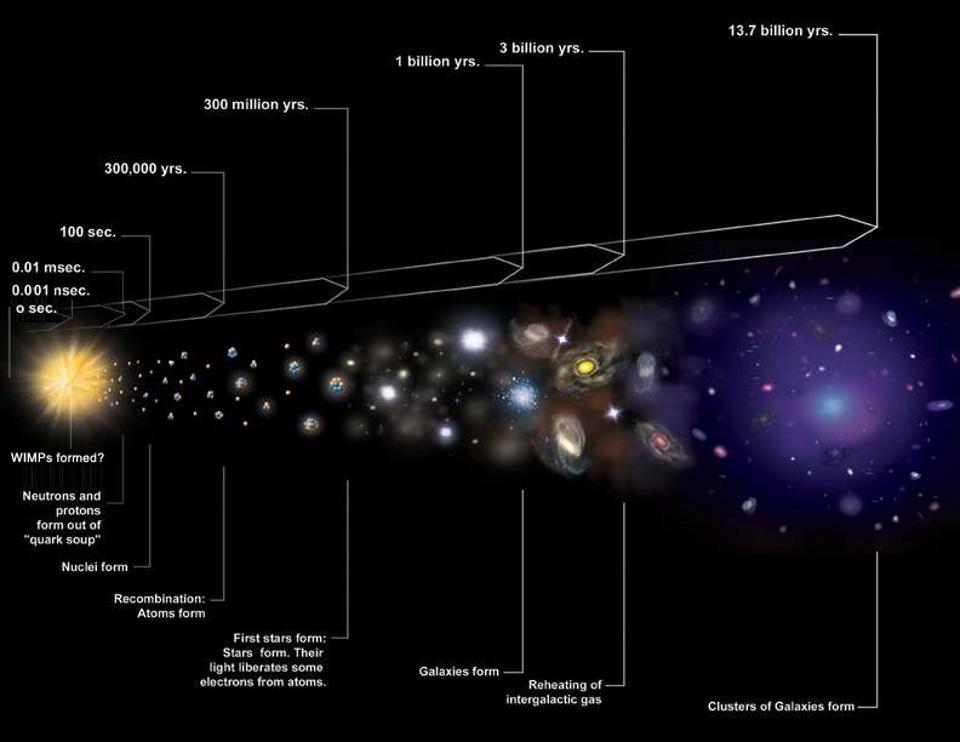
There are plenty of things left over from the Big Bang, including:
- stars
- gas
- dust
- planets
- stellar corpses
However, all of the items we just listed only compose about 2 to 2.5% of the total energy budget of what’s present in the Universe: only about half of the normal matter. There’s also dark matter, dark energy, neutrinos, photons, and a sparse, tenuous, ionized plasma present in space, with the last being known as the WHIM: the warm-hot intergalactic medium.
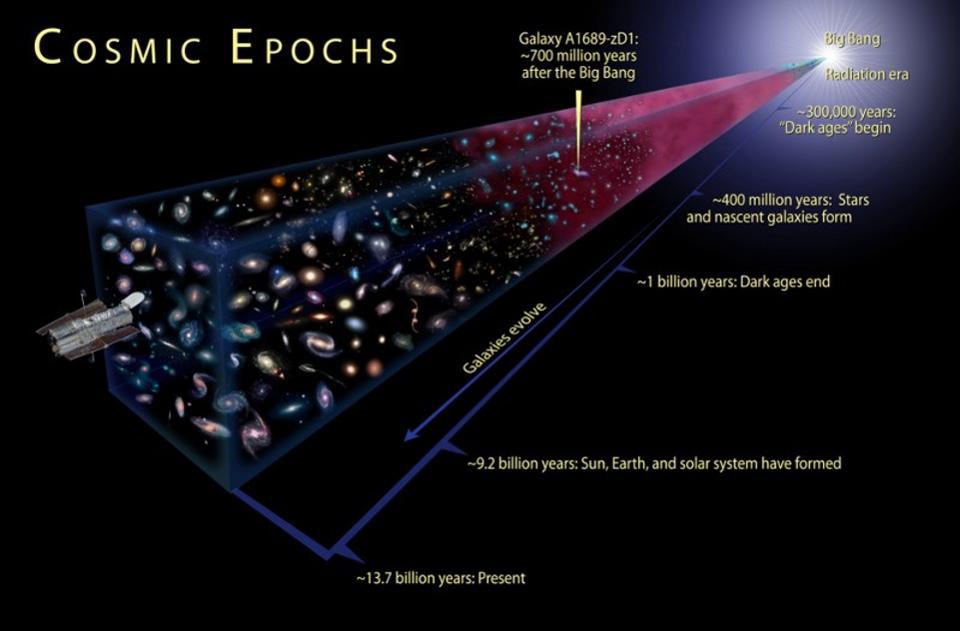
However, the biggest hinderance to charged particles traveling freely through the Universe is actually the least energetic component of all of these: the photons, or leftover particles of light from the Big Bang. While starlight is copious within an individual galaxy, there are places in the Universe — such as the remote depths of intergalactic space — where the only substantial quanta present are the photons left over from the Big Bang: the cosmic microwave background radiation, or CMB. Even today, in our Universe that’s expanded and cooled to be 46.1 billion light-years in radius, there are still around 411 CMB photons per cubic centimeter of space, with an average temperature of 2.7 K.
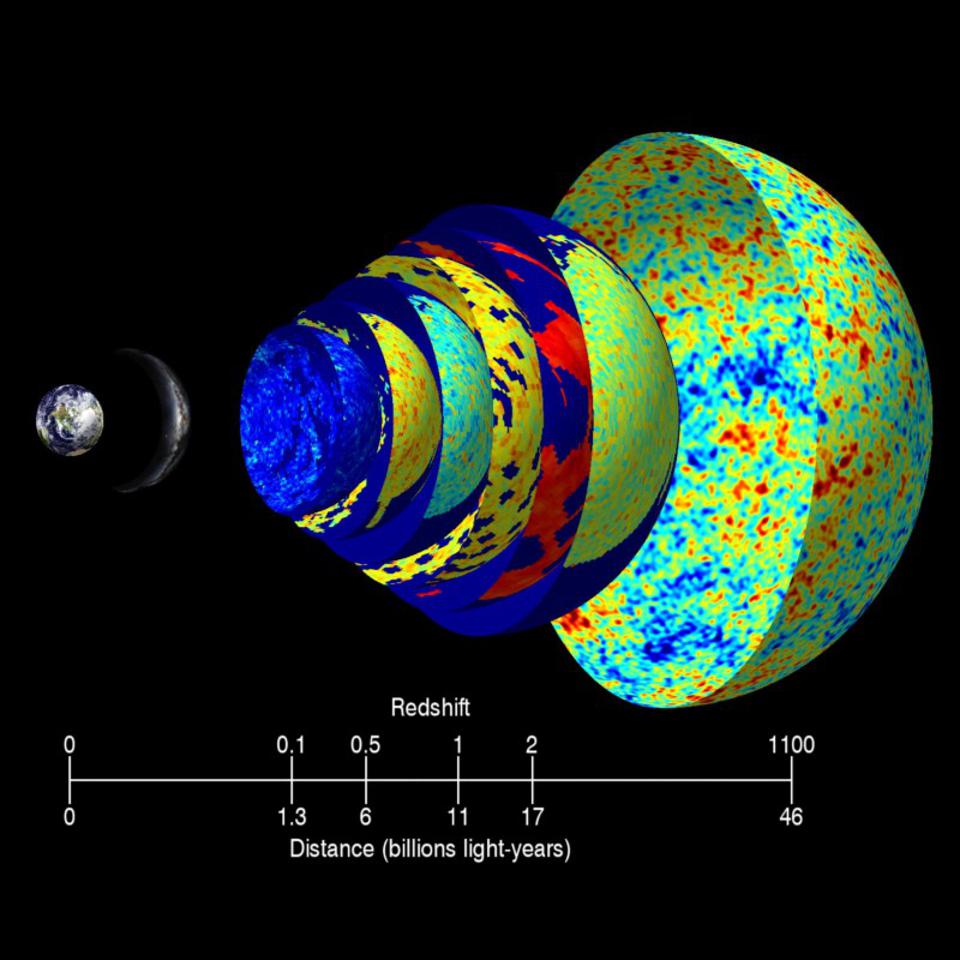
Credit: Earth: NASA/BlueEarth; Milky Way: ESO/S. Brunier; CMB: NASA/WMAP
Now, let’s imagine that we’ve got a natural particle accelerator like a neutron star or a black hole, creating electric and magnetic fields that are unheard of on Earth. In these extreme environments, millions of times the mass of Earth exists in a volume of space no larger than a few kilometers in diameter. These astrophysical locations often can achieve field strengths that are millions, billions, or even trillions of times in excess of the strongest electromagnetic fields ever generated in laboratories on Earth.
Any particle accelerated by these objects will be sent on an ultra-relativistic journey through the Universe, where it will inevitably encounter all sorts of particles. But it will particularly run into the most numerous of all particles: the CMB photons that are present. With around ~1089 CMB photons filling our observable Universe, they’re the most abundant and evenly distributed type of quanta present in our cosmos. Importantly, there’s always a probability for a charged particle and a photon, regardless of what the relative energies of the particle and the photon are, to interact.

(Credit: IceCube collaboration/NASA)
If there were no other particles — if we could activate our “toy” vision of an empty Universe where particles simply traveled unimpeded in a straight line until they reached their destination — we could imagine that only the field strengths of these astrophysical environments would place a cap on the total amount of energy a particle could possess. Apply a strong electric field in the direction it’s moving, and it’ll go faster and become more energetic.
In fact, you’d expect there wouldn’t be a limit at all. If this were how the Universe worked, you’d expect there’d be some sort of energy distribution of particles: where large numbers of particles had low energies and a few outlier particles had higher energies. As you looked to higher and higher energies, you’d keep finding particles, but they’d be fewer in number. The slope of the line might change as various physical processes became important at certain energies, but you wouldn’t expect particles to simply stop existing at some energy; you’d just expect there to be fewer and fewer of them until you reached the limit of what you can detect.

Credit: ASPERA/G.Toma/A.Saftoiu
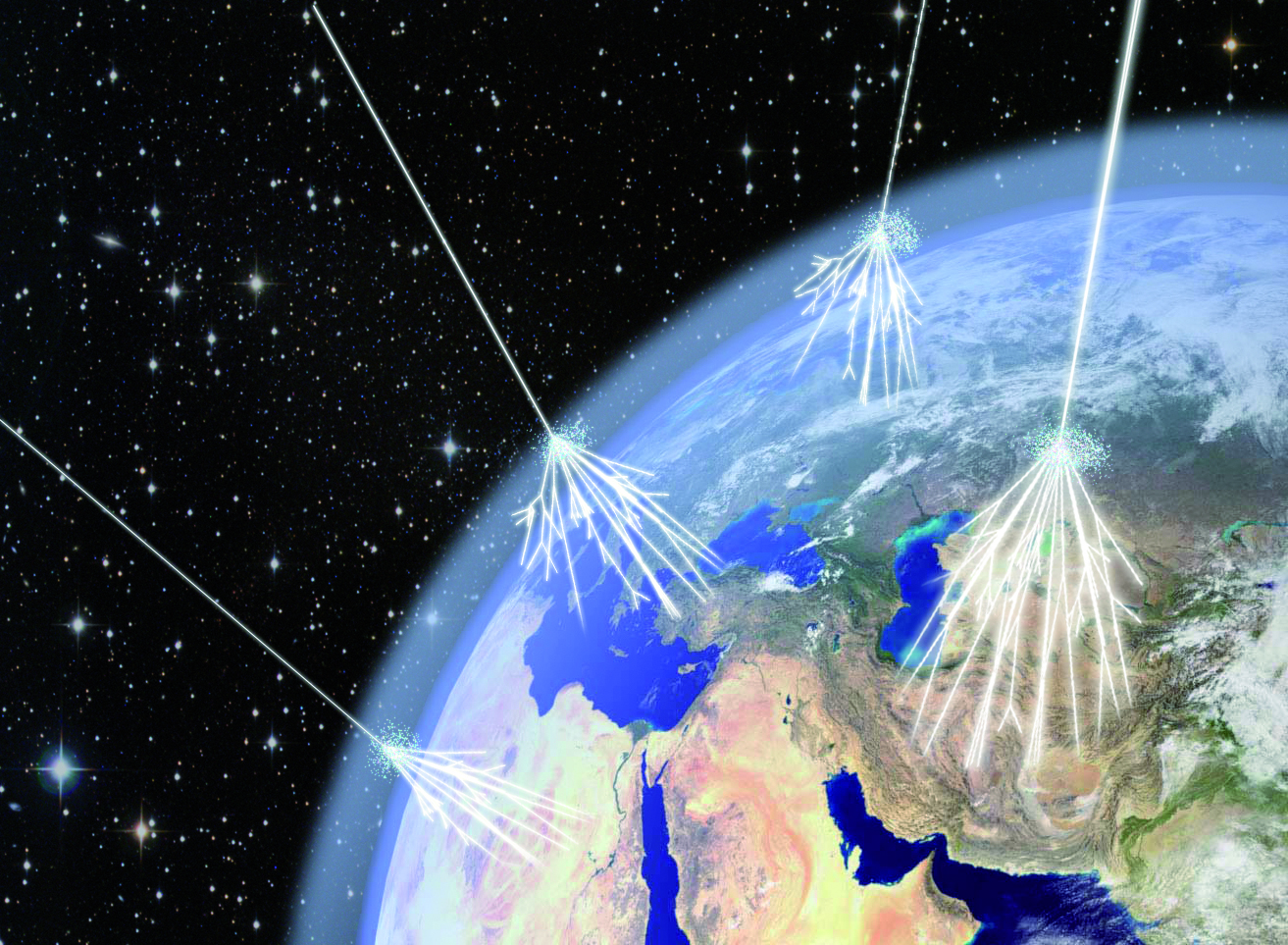
Today, our best modern cosmic ray observatories include large ground-based detectors that grab two main signals:
- Particle showers, identifiable through an array of large-area detectors, such as those leveraged at the Pierre Auger Observatory
- Cherenkov radiation detectors, which grab the characteristic glow of “blue light” (and also ultraviolet light) produced by fast-moving particles that exceed the speed of light in the medium of air, such as the HAWC telescope
At the top of the atmosphere, cosmic ray particles slam into ions, molecules, and atoms at the edge of the Earth. Through a series of chain reactions, they produce what we call “daughter particles” that are all, in some sense, direct descendants of the cosmic rays that initially impacted us. When we detect enough of the daughter particles (their descendants, in other words) that make it down to Earth’s surface, we can reconstruct the initial energies and properties of the cosmic rays that struck us.
While we do, in fact, notice that there are much greater numbers of lower-energy particles than higher-energy ones, and that there are “kinks” in the graph where certain astrophysical phenomena suddenly become important, there also seems to be a cutoff: a point where no particles are seen to exist above a certain energy.
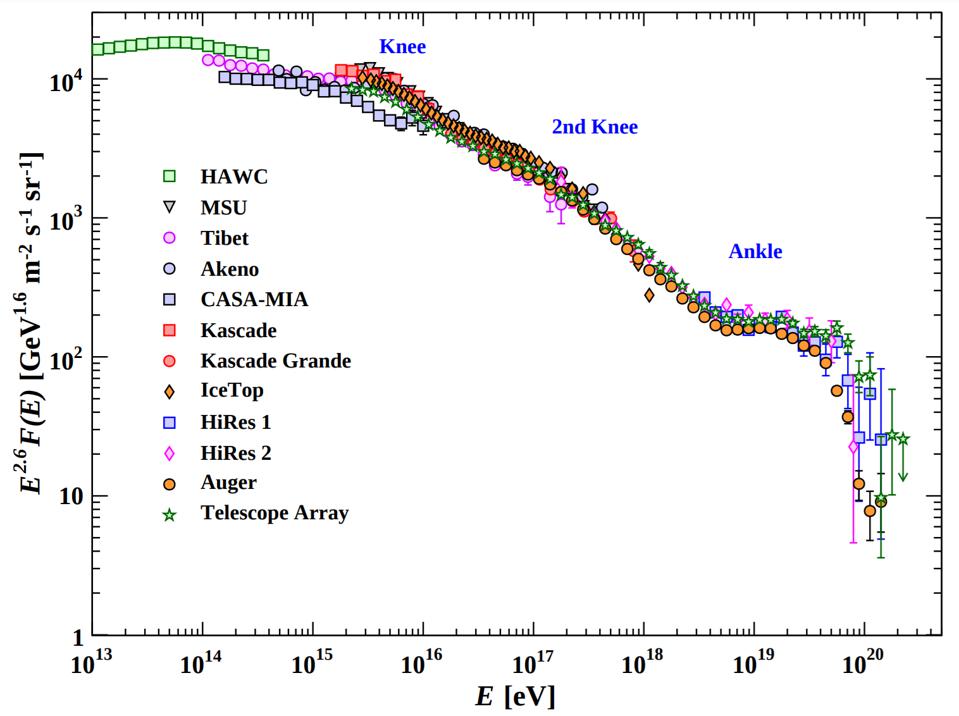
Credit: M. Tanabashi et al. (Particle Data Group), Phys. Rev. D, 2019
What could cause this cutoff to exist?
This is where the idea of the cosmic microwave background comes into play. Remember: Light is an electromagnetic wave, and it interacts with charged particles. At low energies, this is simply Thomson or Compton scattering: where the charged particle and the photon exchange energy and momentum, but very little else occurs. Importantly, this is an extremely inefficient way of stealing energy from a fast-moving particle, even at high energies.
But once your particle hits a certain energy — which, for protons, the overwhelmingly most common type of cosmic ray, is ~1017 electron-volts — the photons appear energetic enough to the cosmic particle that they sometimes behave as though they’re actually made of electron-positron pairs. In the center-of-momentum frame, the proton perceives the photon as having a little over 1 Mega-electron-volts of energy, boosted from its typical CMB value of ~200 micro-electron-volts. Importantly, this is enough energy to produce, via Einstein’s famous E = mc2, an electron-positron pair.
Once cosmic rays, like protons, start colliding with electrons and positrons instead of just photons, they shed energy much more rapidly. With each collision between a cosmic ray and an electron or positron, the original cosmic ray loses about 0.1% of its original energy.
(Credit: Douglas M. Gingrich/University of Alberta)
Even over the millions or billions of light-years that cosmic particles travel, however, this shouldn’t be enough to place a hard cap on the total energy that particles possess; it should simply lower the detected abundance of particles above ~1017 eV in energy. However, there should be a cap, and that’s set by whenever the center-of-momentum energy rises high enough that a much more energetic particle can be created via E = mc2: the pion. In particular, the neutral pion (π0), which requires ~135 Mega-electron-volts of energy to create, will drain each cosmic ray proton’s energy by about 20%.
For any proton, therefore, that exceeds a critical energy threshold for creating neutral pions, there should only be a short amount of time it should be allowed to exist before interactions with CMB photons drag it down below that energy cutoff.
- For protons, that limiting energy is ~5 × 1019 electron-volts.
- The cutoff of that energy value is known as the GZK cutoff after the three scientists who first calculated and predicted it: Kenneth Greisen, Georgiy Zatsepin, and Vadim Kuzmin.
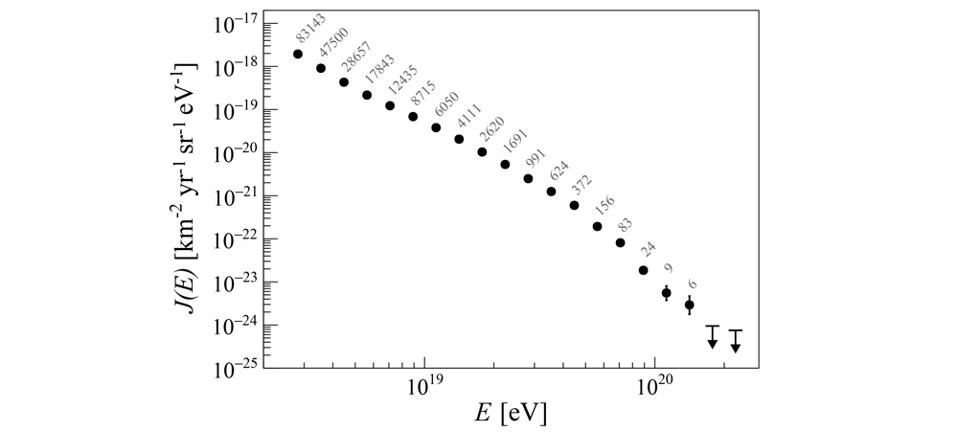
And yet, when we compare the predicted value of where this energy cutoff should be with where the energy cutoff is actually observed, we get a surprise.
Although there’s an extremely severe drop in the number of cosmic rays recorded above that expected cutoff, there have been hundreds of events confirmed to exceed that energy. In fact, they go up to a maximum observed energy of ~5 × 1020 electron-volts — approximately 10 times the expected “maximum” value. Moreover, they’re not correlated with suspected nearby sources, like identified neutron stars or supermassive black holes, nor are they clumped or clustered together. They appear to come from random directions, but with energies that exceed the expected maximum limit.
How is this possible? Does this mean the Universe is “broken” in some way?
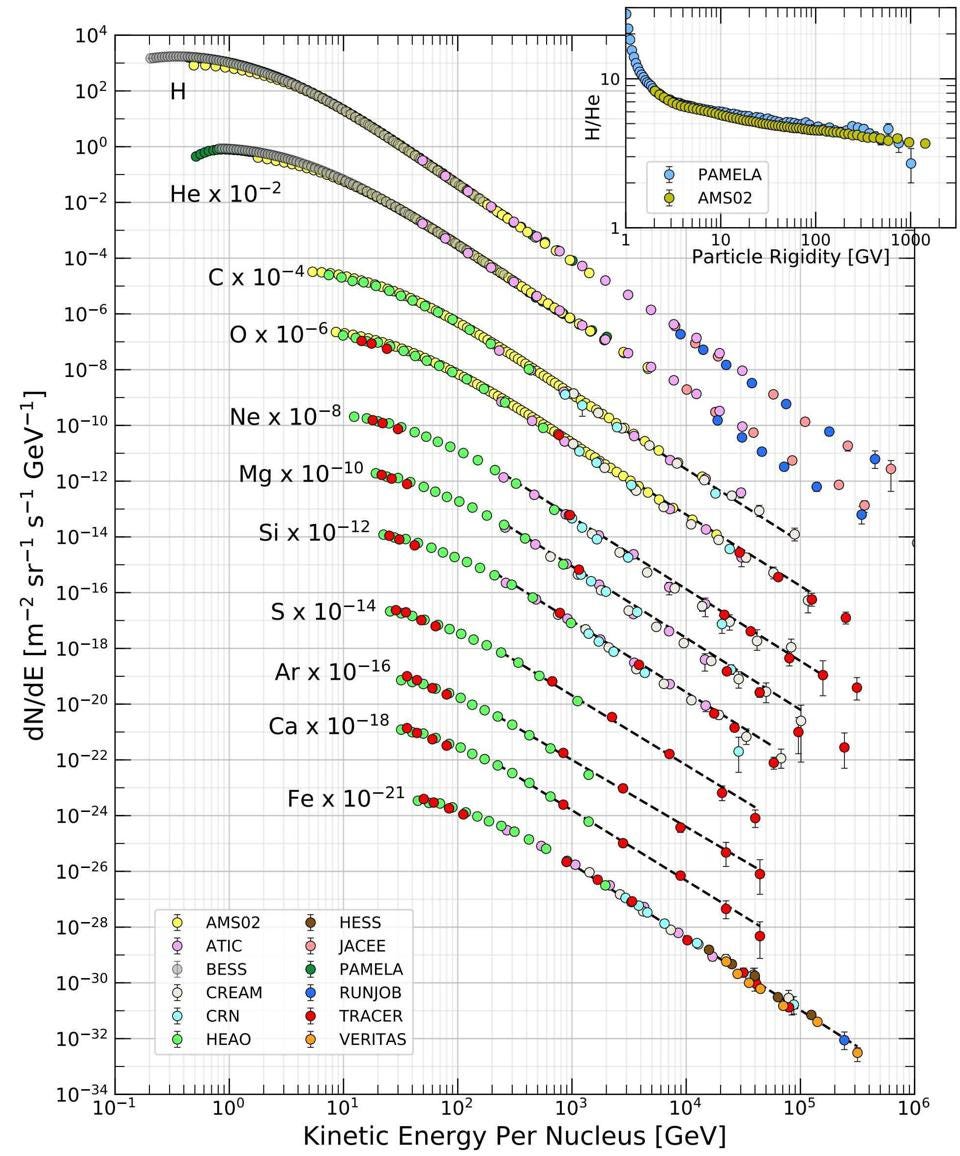
Credit: M. Tanabashi et al. (Particle Data Group), Phys. Rev. D, 2019
Before you start thinking of fanciful explanations like “Einstein’s relativity is wrong,” it’s worth remembering something important. Most cosmic rays are protons. However, a small but significant fraction of them are heavier atomic nuclei: helium, carbon, oxygen, neon, magnesium, silicon, sulphur, argon, calcium, all the way up to iron. But whereas hydrogen is the most common nucleus as a single proton, iron typically has a mass that’s 56 times as heavy, with 26 protons and 30 neutrons. If we consider that the most energetic particles might be made out of these heaviest atomic nuclei rather than mere protons, the paradox vanishes and the GZK “speed limit” remains intact.
Although it was quite a surprise when the first particle exceeding the GZK limit was discovered back in 1991 — so surprising that we named it the Oh-My-God particle — we now understand why that’s possible. There isn’t an energy limit for cosmic rays, but a speed limit: one that’s approximately 99.99999999999999999998% the speed of light. Whether your particle is made only of a single proton or many protons and neutrons bound together isn’t important. What’s important is that, above that critical speed, collisions with photons left over from the Big Bang will create neutral pions, which cause you to lose energy rapidly. After only a handful of collisions, you’ll be compelled to drop below that critical speed, consistent with both observation and theory.
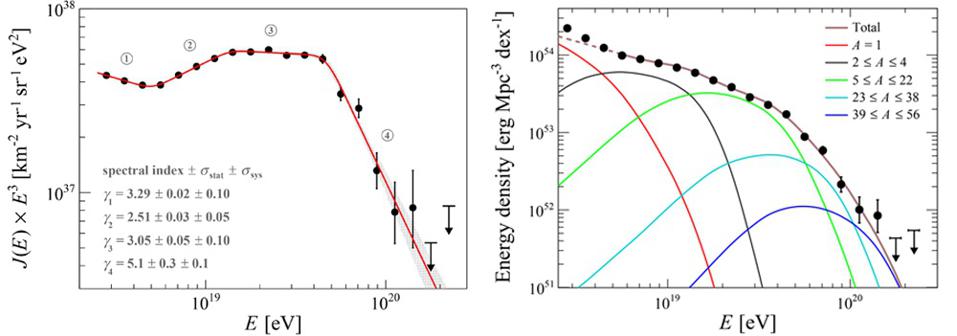
Credit: Pierre Auger Collaboration, Phys. Rev. Lett., 2020
It’s true that no massive particles can ever reach or exceed the speed of light, but that’s just in theory. In practice, you have to move about ~60 femtometers-per-second slower than the speed of light, or collisions with the leftover photons from the Big Bang will spontaneously produce massive particles — neutral pions — that rapidly cause you to shed energy until you’re traveling below that slightly more restrictive speed limit. Additionally, the most energetic ones aren’t faster than they should be. They’re just more massive, with their kinetic energy spread out over scores of particles instead of a single proton. Overall, particles not only can’t reach the speed of light, but can’t even maintain their speed if they’re too close to it. The Universe, and specifically the leftover light from the Big Bang, ensures that it’s so.