There must be a singularity at each black hole’s center

The more mass you place into a small volume of space, the stronger the gravitational pull gets. According to Einstein’s general theory of relativity, there’s an astrophysical limit to how dense something can get and still remain a macroscopic, three-dimensional object. Exceed that critical value and you’re destined to become a black hole: a region of space where gravitation is so strong that you create an event horizon and a region from within which nothing can escape.

No matter how fast you move, how quickly you accelerate, or even if you move at the ultimate speed limit of the Universe — the speed of light — you can’t get out. People have often wondered whether there might be a stable form of ultra-dense matter inside that event horizon that will hold up against gravitational collapse, and whether a singularity is truly inevitable. It’s a reasonable thing to wonder, as we simply cannot access the region interior to the event horizon; we cannot know the answer directly.

Nevertheless, if you apply the laws of physics as we know them today, you cannot avoid a singularity inside a black hole. Here’s the science behind why.

This computer simulation of a neutron star shows charged particles being whipped around by a neutron star’s extraordinarily strong electric and magnetic fields. The fastest-spinning neutron star we’ve ever discovered is a pulsar that revolves 766 times per second: faster than our Sun would spin if we collapsed it down to the size of a neutron star. Irrespective of their spin rates, neutron stars may be the densest physical objects nature can create without progressing to create a singularity, and typically have surface temperatures of several hundreds of thousands of degrees.

Imagine the densest, most massive object you can create out of matter that falls just short of the threshold for becoming a black hole. This is, unsurprisingly, something that occurs in nature all the time. Whenever massive stars go supernova, they can make either a black hole (if they’re above a critical mass threshold), but more commonly they’ll see their cores collapse to form a neutron star, which is the densest, most massive thing we know of that falls short of becoming a black hole.

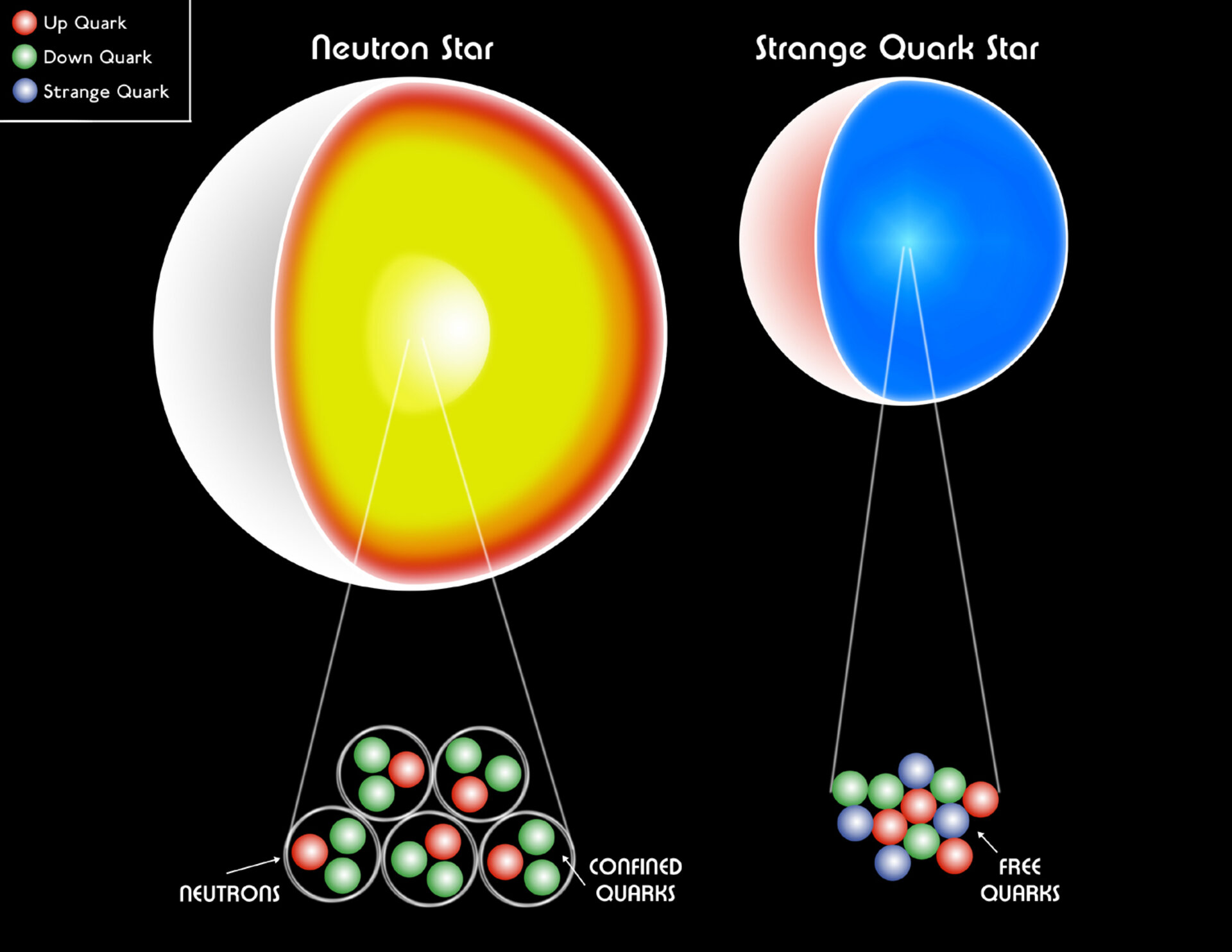
A neutron star is basically an enormous atomic nucleus: a bound-together collection of neutrons that’s even more massive than the Sun but contained in a region of space just a few kilometers across. It’s conceivable that if you exceed the allowed density at the core of a neutron star, it might move on to an even more concentrated state of matter: a quark-gluon plasma, where densities are so great that it no longer makes sense to consider the matter in there as individual, bound structures. Under these conditions, not only up-and-down quarks, but heavier, normally unstable quarks, may become part of the stellar remnant’s interior.

A white dwarf, a neutron star, or even a strange quark star are all still made of fermions. The Pauli degeneracy pressure helps hold up the stellar remnant against gravitational collapse, preventing a black hole from forming. Inside the most massive neutron stars, an exotic form of matter, a quark-gluon plasma, is thought to exist, with temperatures rising up to ~1 trillion (10^12) K.

It’s worth asking an important question at this point: how is it that we can we have matter, at all, inside the core of such a dense object?

The only way for this to be possible is if something inside the object is exerting an outward force on the material exterior to it, holding the center up against gravitational collapse.

For a low-density object like Earth, the electromagnetic force is enough to do it. The atoms that we have are made of nuclei and electrons, and the electron shells push against each other. We also have the quantum rule of the Pauli Exclusion Principle, which prevents any two identical fermions (like electrons) from occupying the same quantum state.

Under any circumstances where there isn’t an internal source of radiation pressure, like the pressure that arises from nuclear fusion processes inside of active stars, the Pauli Exclusion Principle is one of the primary ways that such an object resists gravitationally collapsing any further. This holds for matter as dense as a white dwarf star, where a stellar-mass object can exist in a volume no greater than the size of Earth.

An accurate size/color comparison of a white dwarf (left), Earth reflecting our Sun’s light (middle), and a black dwarf (right). When white dwarfs finally radiate the last of their energy away, they will all eventually become black dwarfs. The degeneracy pressure between the electrons within the white/black dwarf, however, will always be great enough, so long as it doesn’t accrue too much mass, to prevent it from collapsing further.

If you place too much mass on a white dwarf star, however, the individual nuclei themselves will undergo a runaway fusion reaction, as the quantum overlap of their wavefunctions becomes too great. As a consequence of this process, there’s a limit to how massive a white dwarf star can get: the Chandrasekhar mass limit.

Inside a neutron star, there are no atoms at the core, but rather it behaves as one enormous atomic nucleus, made almost exclusively of neutrons. (The outer ~10% of neutron stars may be made of other nuclei, including those that contain protons, but the innermost portions are either composed of neutrons or a quark-gluon plasma.) Neutrons also act as fermions — despite being composite particles — and quantum forces also work to hold them up against gravitational collapse.

It’s possible, beyond that, to imagine another, even denser state: a quark star, where individual quarks (and free gluons) interact with each other, still obeying the rule that no two identical quantum particles can occupy the same quantum state.

The Pauli exclusion principle prevents two fermions from coexisting in the same quantum system with the same quantum state. It only applies to fermions, however, like quarks and leptons. It does not apply to bosons, and hence there is no limit to, say, the number of identical photons that can coexist in the same quantum state. It’s why fermion-containing stellar remnants, like white dwarfs and neutron stars, can hold themselves up against gravitational collapse, as the Pauli Exclusion Principle limits the volume that a finite number of fermions can occupy.

But there’s a key realization in the mechanism that prevents matter from collapsing down to a singularity: forces must be exchanged. What this means, if you attempt to visualize it, is that force carrying particles (like photons, gluons, etc.) must be exchanged between the various fermions in the interior of the object.

Here’s a refresher on the basics of how our quantum Universe works.

1. All of the matter we know of is made, fundamentally, out of discrete quantum particles.
2. Those particles come in two types: fermions (which obey the Pauli rule) and bosons (which ignore it), but electrons and quarks, as well as protons and neutrons, are all fermions.
3. Gravitation, which we believe (but aren’t yet certain) is inherently a quantum force, can be well-described by General Relativity up until we obtain singularities; any non-singular state can work within General Relativity.
4. In order to resist the inward pull of gravity, some quantum exchange must happen between the interior and the exterior of a volume-containing object, otherwise everything will continue to collapse inward.
5. But those exchanges, regardless of the force, are fundamentally limited by the laws of physics themselves: including both relativity and quantum mechanics.

The strong force, operating as it does because of the existence of ‘color charge’ and the exchange of gluons, is responsible for the force that holds atomic nuclei together. This force, governed by the exchange of massive gluons, is bounded by the speed of light; from inside a black hole’s event horizon, there’s no way that a force such as this can prevent any outermore particle from reaching the central singularity.

The thing is, there’s a speed limit to how fast these force-carriers can go: the speed of light. If you want an interaction to work by having an interior particle exert an outward force on an exterior particle, there needs to be some way for a particle to travel along that outward path. If the spacetime containing your particles is below the density threshold necessary to create a black hole, that’s no problem: moving at the speed of light will allow you to take that outward trajectory.

But what if your spacetime crosses that threshold?

What if you create an event horizon, and have a region of space where gravity is so intense that even if you moved at the speed of light, you couldn’t escape?

One way to visualize this it to think about space as flowing, like a waterfall or a moving walkway, and to think of particles as moving atop that background of flowing space. If space flows faster than your particles can move, you’ll be drawn inward, toward the center, even as your particles attempt to flow outward. That’s why the event horizon, where particles are limited by the speed of light but space flows faster than particles can move, is of such profound importance.

Both inside and outside the event horizon of a Schwarzschild black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. At the event horizon, even if you ran (or swam) at the speed of light, there would be no overcoming the flow of spacetime, which drags you into the singularity at the center. Outside the event horizon, though, other forces (like electromagnetism) can frequently overcome the pull of gravity, causing even infalling matter to escape. This spacetime conserves energy, as it’s time-translation invariant.

Now, from inside the event horizon, the outward-propagating forces don’t actually propagate outward. All of a sudden, there’s no path at all that will work to hold the outsides up against collapse! The gravitational force will work to pull that exterior particle inward, but the force-carrying particle coming from the interior particle simply cannot move outward.

Inside a dense-enough region, even massless particles have nowhere to go except toward the most interior points possible; they cannot influence exterior points. So the exterior particles have no choice but to fall in, closer to the central region. No matter how you set it up, initially, every single particle inside the event horizon inevitably winds up at a singular location: the singularity at the black hole’s center.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

This happens even if the black hole isn’t a stationary point mass, but has either electric charge and/or spin and angular momentum to it. The specifics of the problem change, and (in the case of rotation) the central singularity might be smeared out into a one-dimensional ring instead of a zero-dimensional point, but there’s no way to hold it up. Collapse down to a singularity is inevitable.

In the vicinity of a black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. Unlike in the non-rotating case, the event horizon splits into two, while the central singularity gets stretched out into a one-dimensional ring. Nobody knows what occurs at the central singularity, but its presence and existence cannot be avoided with our current understanding of physics.

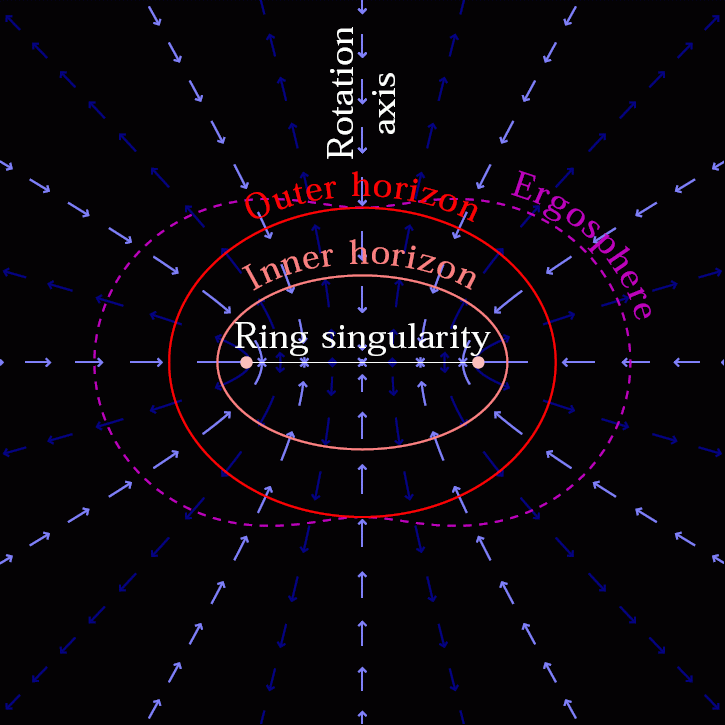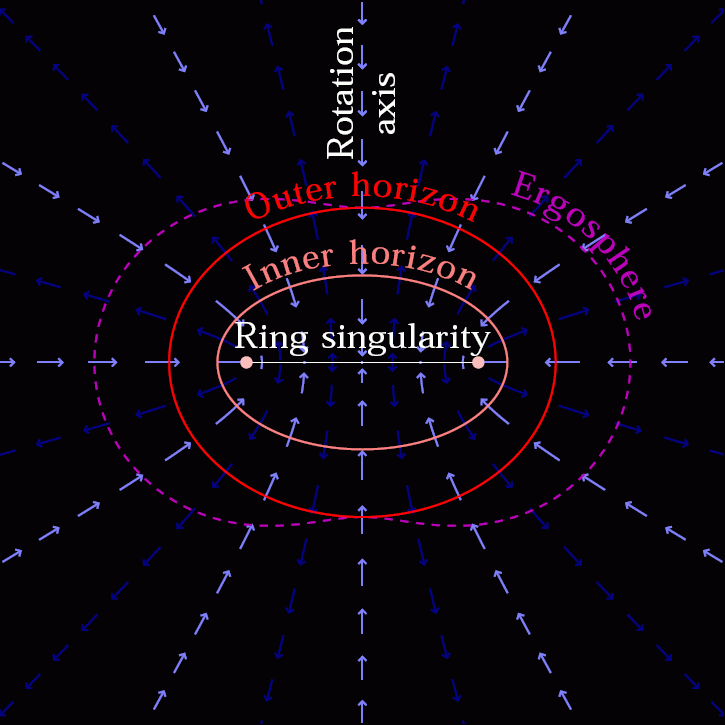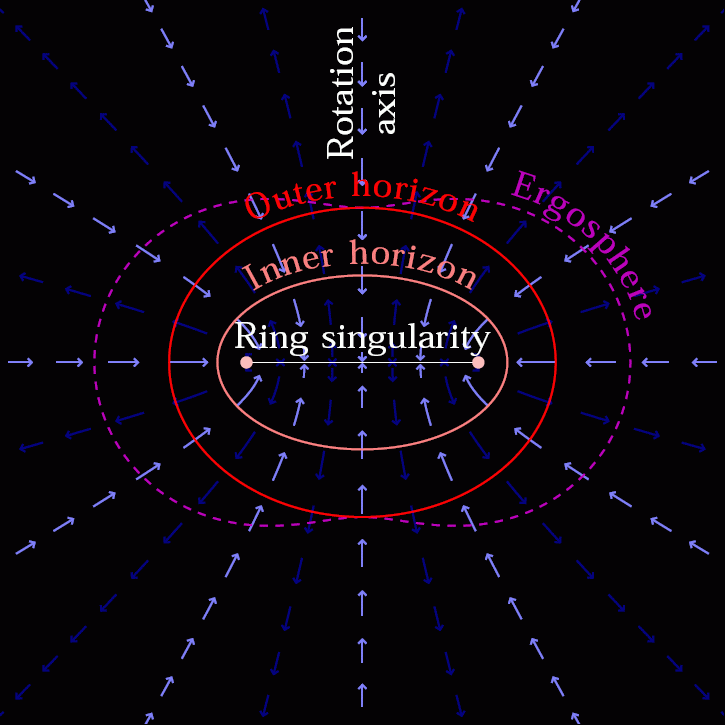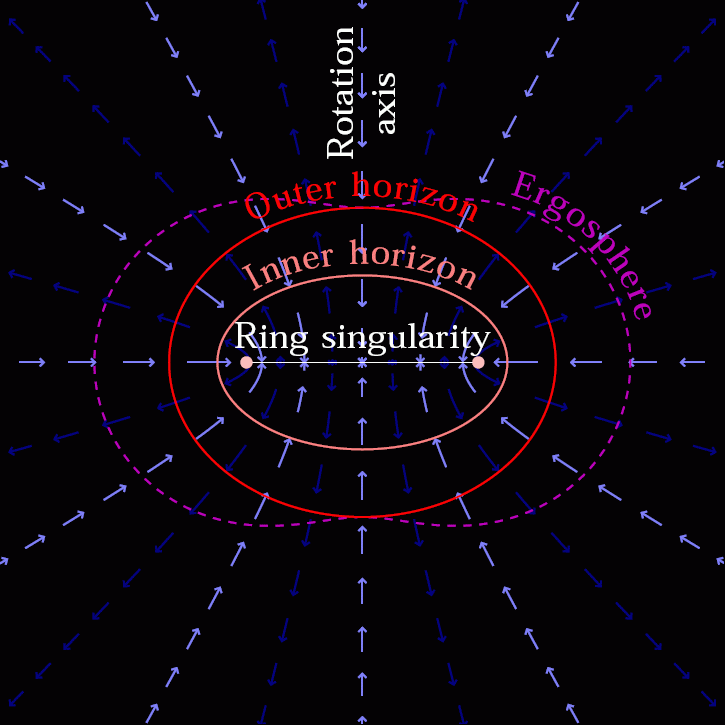
You might then ask, “Okay, so what do I do if I want to create a situation where, inside of this black hole, I do have some sort of degenerate, volume-containing entity that doesn’t collapse completely down to a singularity?”

The answer, in all cases, requires that you have some sort of force or effect that can propagate outward, affecting quanta that are farther away from the central region than the interior particle, at speeds that exceed the speed of light. What kind of force can that be?

• It cannot be the strong nuclear force.
• Or the weak nuclear force.
• Or the electromagnetic force.
• Or the gravitational force.

And that’s a problem, because that is all of the known fundamental forces that exist. In other words, you need to postulate some new, hitherto undiscovered force in order to avoid a central singularity inside of your black holes, and that force needs to do something that no known force or effect can do: violate the principle of relativity, affecting objects around it at speeds that exceed the speed of light.

One of the most important contributions of Roger Penrose to black hole physics is the demonstration of how a realistic object in our Universe, such as a star (or any collection of matter), can form an event horizon and how all the matter bound to it will inevitably encounter the central singularity. Once an event horizon forms, the development of a central singularity is not only inevitable, it’s extremely rapid.

Quite simply, that scenario conflicts with what is presently known about our physical reality. So long as particles — including force-carrying particles — are limited by the speed of light, there’s no way to have a stable, non-singular structure inside a black hole. If you can invent a tachyonic force, which is to say a force mediated by particles that move faster-than-light, you might be able to create one, but so far no real, tachyon-like particles have been shown to physically exist. In fact, in every quantum field theory where they’ve been introduced, they must decouple from the theory (becoming ghost particles), or they exhibit pathological behavior.

Without a novel faster-than-light force or effect, the best you can do is “smear out” your singularity into a one-dimensional, ring-like object (due to angular momentum), but that still won’t get you a three-dimensional structure. So long as your particles either have positive mass or zero mass, and so long as they obey the rules of physics we know, a singularity at the center of every black hole is an inevitability. There can be no real particles, structures, or composite entities that survive a journey into a black hole. Within seconds of forming an event horizon, all that can ever exist at its center is reduced to a mere singularity.