Scientists Discover The Fastest Star Around A Supermassive Black Hole

If there are cracks in Einstein’s theory, this is how to find them.

Is Einstein’s most powerful theory, General Relativity, always correct? Or will there come a point where it breaks down, and requires a new innovation like quantum gravity to accurately describe our Universe? It’s one of the biggest undecided questions in all of physics. Mass and energy both curve space, and that curved space then determines how all objects — massive and massless — will move. In every way we’ve ever put Einstein’s relativity to the test, at both high speeds and where space is curved the most severely, it’s passed with flying colors.

But the way science progresses is by pushing these limits to ever greater extremes. For velocity, that means we want massive objects that get as close to the speed of light as possible. For maximizing how severely space is curved, we want to get as close to the edge of a black hole’s event horizon as possible. And in the ideal case, we’d get both of them together: fast-moving masses close to a black hole’s event horizon. In a new study published August 11, 2020, scientists have just found the most extreme objects ever: the fastest stars that get the closest to the edge of a supermassive black hole. Here’s what we know about this exciting new discovery.

When objects move close to the speed of light, they experience both space and time differently from how we conventionally conceive of them. We typically think of distances as fixed: if you have a ruler and I have an identical ruler, you’d think that the distances we each measure between two points using that ruler will be identical. Same with time: if I have a clock and you have an identical clock, you’d expect that the time we each measure between two agreed-upon events will also be identical.

But that’s not how things work under the rules of relativity at all. The closer an object moves to the speed of light — relative to you, the observer — the greater the amount that both:

1. distances are contracted along its direction-of-motion, and
2. time is dilated, meaning that its clock is running slower from your perspective.

In addition, the fact that an object is in motion relative to you, either moving towards you or away from you, means that its light will be systematically shifted towards either the blue or the red portion of the spectrum, respectively.

This effect — known as the Doppler shift — is the same reason that police sirens (or ice cream truck jingles) sound higher pitched when they’re moving towards you, but lower pitched when they move away from you. An object moving towards you while it emits a wave, whether it’s a sound wave or a light wave, will have its waves peaks-and-valleys shortened, reducing its wavelength. For light, that results in a blueshift; for sound, that results in a higher pitch. Conversely, an object moving away from you has its wavelength lengthened, resulting in a redshift for light or a shift towards lower pitches for sound.

When we observe a star in our own galaxy, we can determine whether it’s moving towards us or away from us by looking at the light it emits: specifically, from the light emitted (or absorbed) by the elements contained within it. This is extremely useful for light because all of the emission (or absorption) lines that come from an element, such as hydrogen, will be shifted by the same amount. Moreover, if we have a star in orbit around another object, we can actually observe the redshift and blueshift cycle over time, teaching us about the “gravitational dance” that’s occurring.

These same three effects that occur due to the relative motion between the source and the observer,

• length contraction,
• time dilation,
• and a redshifting/blueshifting of light,

also occur when either the source, the observer, or both are influenced by the gravitation of another mass. Einstein first realized that this must occur more than a century ago, calling the realization “his happiest thought.”

We now know it as the equivalence principle, as it states that someone experiencing an acceleration cannot tell whether that acceleration is due to a gravitational effect or a non-gravitational effect, such as a thrust or an external force. The effects of a gravitational redshift or blueshift, in particular, are very important in the context of a star orbiting another massive body. When it’s at its closest to the other mass, it will both be moving the fastest (giving it a large Doppler shift), and it will also be the deepest in the mass’s gravitational field (giving it a large gravitational redshift). These two effects must both be taken into account if we hope to put Einstein’s relativity to the test.

The best place to test Einstein’s relativity will be where these relativistic effects are largest. That means we want to look at stars that pass as close as possible to the event horizon of a black hole. The event horizon, remember, is the invisible border between where an object could, in theory, escape, and that point-of-no-return, where anything that crosses it will inevitably drawn into the black hole’s central singularity. Once any object crosses the event horizon, nothing — not even light — can ever get out again.

The problem is that stars are relatively large objects, and that if you get too close to a black hole’s event horizon, the tidal forces will wind up tearing that star apart. This can result in a class of stellar cataclysms known as tidal disruption events, which lead to large amounts of nuclear fusion and result in the death of the star. This effectively prohibits us from looking at stars in orbit around stellar mass black holes, as that’s where tidal forces are strongest. We’ve seen these tidal disruption events, and have concluded that it’s simply too easy for these small black holes to tear stars apart.

On the other hand, supermassive black holes don’t really have this problem in the same way. While they still have the same event horizons as their low-mass counterparts — where any object that crosses it can never escape — the tidal forces near them are much, much lower. This makes them the ideal place to look for stars that are simultaneously:

• moving close to the speed of light, where relativistic effects (due to speed) are observable,
• and are close to another large mass, where the relativistic effects (due to gravitation) are observable.

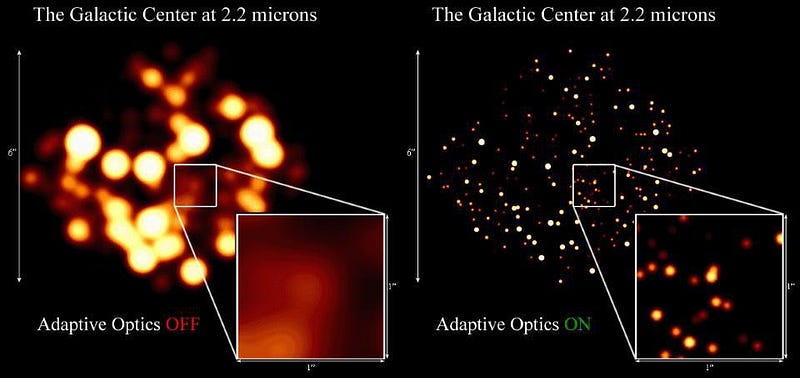
The closest supermassive black hole to us is Sagittarius A*: the black hole at the center of our Milky Way, located a mere 26,000 light-years away. (The next closest one, at the center of Andromeda, is more than 2 million light-years distant!) Beginning in the mid-1990s, advances in observational tools and techniques — particularly in ground-based adaptive optics and in infrared instrumentation — enabled us to see through the galactic dust and resolve individual stars that are in our galaxy’s central region. Not only that, but we’ve imaged and tracked them over time, revealing and reconstructing their orbits.

This combination of factors has given us an unprecedented strong-field test of Einstein’s General Relativity. When you’re at large distances from weakly gravitating sources and at low speeds compared to the speed of light, Newton’s gravitation and Newton’s laws of motion are outstanding approximations for the laws of physics. Relativity’s effects only reveal themselves at small distances from strongly gravitating sources and at large speeds compared to the speed of light, which enables us to not only test Einstein’s theories, but to search for evidence of where relativity might break down and be superseded by a new, hitherto undiscovered theory of gravity.

The closest stars we’ve ever found to the Milky Way’s central black hole are:

• highly eccentric (where they get very close to the black hole and then very far away from it),
• take only about ~10–20 years to complete an orbit (about the time it takes Jupiter to orbit the Sun),
• come within only about 20 billion kilometers of the event horizon (about 120 times the Earth-Sun distance),
• and reach maximum speeds of a few percent the speed of light.

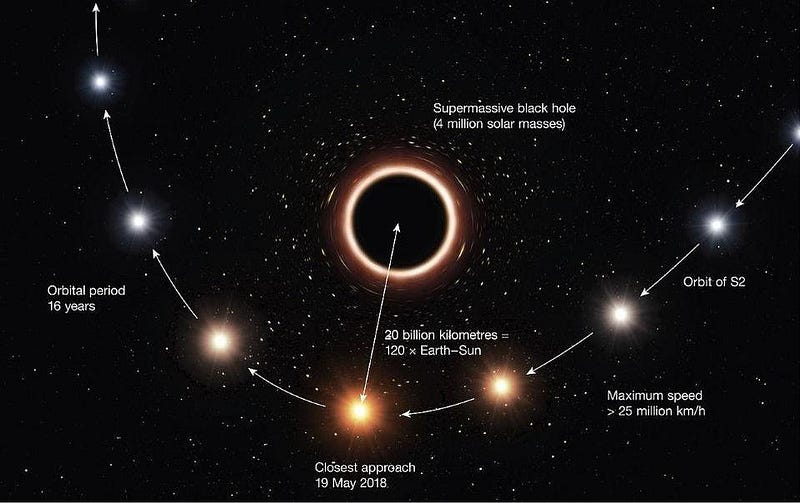
In 2018, the star known as S2 — one of the first stars ever discovered so close to the galactic center — made an extremely close pass to our supermassive black hole, reaching 2.7% the speed of light and performing the strongest-field test of General Relativity to date. In a surprise to no one, two independent teams analyzed the close pass, and both the Ghez group and the GRAVITY collaboration found that the results showed that Newtonian gravity was wrong, confirmed Einstein’s relativity, and ruled out any alternatives that differed from Einstein’s theory substantially.

But there ought to be many more stars that are fainter than S2, and many of them should get closer to our galaxy’s central black hole, move faster, and see the position of their closest approach precess more quickly than S2 does. In short, they should provide a better, more restrictive, and more fundamental test of relativity than ever before. Additionally, they should orbit more quickly, on timescales of less than a decade. We want to test relativity more precisely than ever before, and this is one approach to doing so.

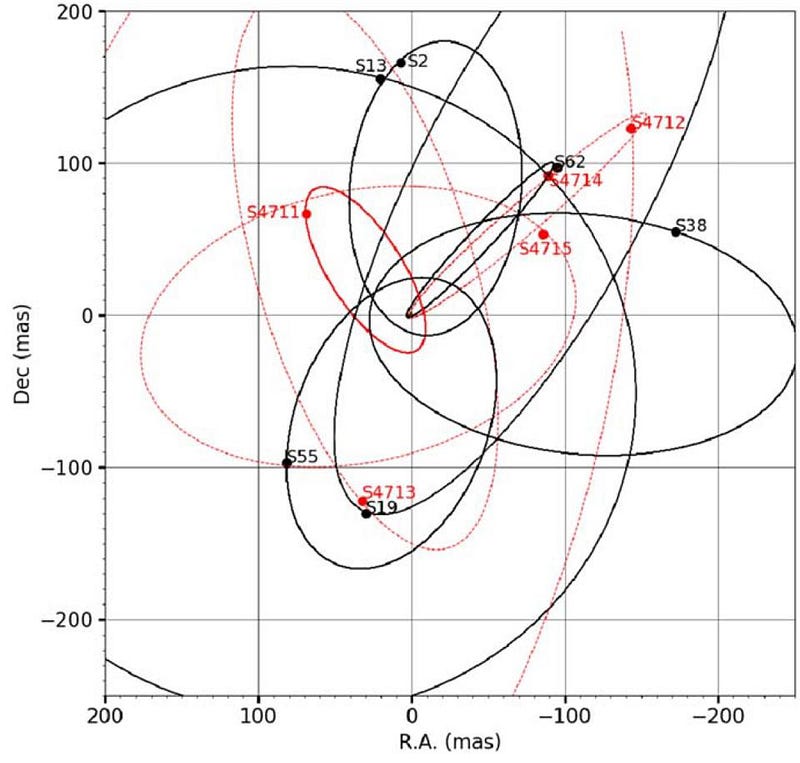
On August 11, the astronomers looking for exactly these types of stars published an Astronomer’s Telegram, announcing the discovery of a set of new stars in the central cluster of our galaxy. In particular, two of these stars just broke all previous records for how well they’ll enable us to test Einstein’s relativity: S4711 and S4714. The important things to know are as follows:

• Both S4711 and S4714 are faint, at around 18th magnitude, but can be seen with today’s modern infrared telescopes.
• Each one is about twice the mass of the Sun, and both have highly eccentric, elliptical orbits.
• Both orbit quickly: S4711 completes a revolution around the galactic center every 7.6 years, the shortest period ever discovered, while S4714 makes a revolution every 12.0 years.

Even though the uncertainties are large, the star S4714

• comes closer to the central black hole (just 1.9 billion kilometers away from it),
• has the highest maximum velocity (8% the speed of light),
• and experiences the largest predicted precession (both Schwarzschild and Lense-Thirring precessions)

of any star ever measured.

This new discovery leads to two exciting consequences. The first — and most immediate — is that this extreme star, the one that moves fastest and passes closest to our galaxy’s supermassive black hole, will provide us with the strongest test ever performed of Einstein’s General Relativity. With a 12 year orbital period, the next time it makes its closest approach to Sagittarius A* will be in 2029, when we’ll be able to target it with next-generation telescopes like the Giant Magellan Telescope or the European Extremely Large Telescope. With this new star and these new observatories, we’ll have the greatest opportunity we’ve ever had to look for cracks in Einstein’s greatest scientific achievement.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

But the second consequence is that this verifies and validates a number of theoretical predictions of stellar populations that ought to exist but had never been discovered until now. These predictions further indicate that there should be large numbers of even fainter stars that ought to approach our central black hole even more closely, and that these next-generation telescopes should reveal them to us. In the coming decade, we’ll be able to test our theory of gravity like never before. If Einstein’s theory doesn’t match with our observations, it might be the start of the biggest scientific revolution that physics has ever seen.