Rainbows are actually full circles. A physicist explains

- Rainbows are instantly recognizable when they appear: an arc of sunlight reflected off of water drops that spreads out that white light into all of its component colors.
- Typically, most of us experience rainbows as colorful arcs in the sky, occasionally joined by a second, fainter outer bow and/or any reflections in additional bodies of water.
- But the true, full shape of a rainbow is actually a full circle. Normally obscured by Earth’s surface, a full rainbow can be seen under the right conditions. Here’s how.
Think about the last time you saw a rainbow; what was it like? It was probably evidently a “bow,” for starters, where it made its classic arc-like shape, with colors changing from red on the outside through the full spectrum of colors, down to blue/violet on the interior. There may have been a secondary rainbow, fainter and with color-order reversed, above it. The weather conditions were probably a mix of cloudy, rainy skies and cloud-free, sunlit streaks, or otherwise it was likely sunny and you had a lot of mist nearby. And although you probably don’t think of it as being a remarkable occurrence, it was probably daytime and you were probably somewhere on the surface of the Earth.
What you might not realize is that the shape of a rainbow isn’t a “bow” or an “arc” at all, but rather a full circle. The only reason you see part of that full circle, under most conditions, is because the Earth itself (or other foreground features) are in the way, preventing you from seeing the entire rainbow at once.
But there are certain tricks you can use to overcome those terrestrial limits, enabling you to see the full-circle rainbow all at once. These range from flying in an airplane with the Sun on one side and copious rainfall/clouds on the other to simply orienting yourself with your back to the Sun while spraying the fine mist from a garden hose. Here’s the science of how rainbows work, and why they truly are full circles.

There are only three ingredients that you need to make rainbows:
- a source of white light,
- drops of water to reflect that light,
- and an observer with the right geometric perspective to see it.
Rainbows aren’t physically “real objects,” in the sense that if you move toward or away from one, the rainbow will shift in response to your motion. Each observer at each unique location sees their own individual rainbow.
It’s why any attempt to find the proverbial “pot of gold at the end of the rainbow” will always fail, as rainbows don’t have a beginning or end; they’re a purely optical phenomenon, only appearing at a specific set of angles relative to the Sun and the specific location of the person or camera viewing them. The way to understand a rainbow is very similar to understanding why a prism splits light into its various wavelengths and colors. The fundamental principle behind them is one and the same: that light slows down when it travels through a medium, and that even though the speed of light in a vacuum is always a constant, the speed of light through a medium is different for every different color or wavelength of light.
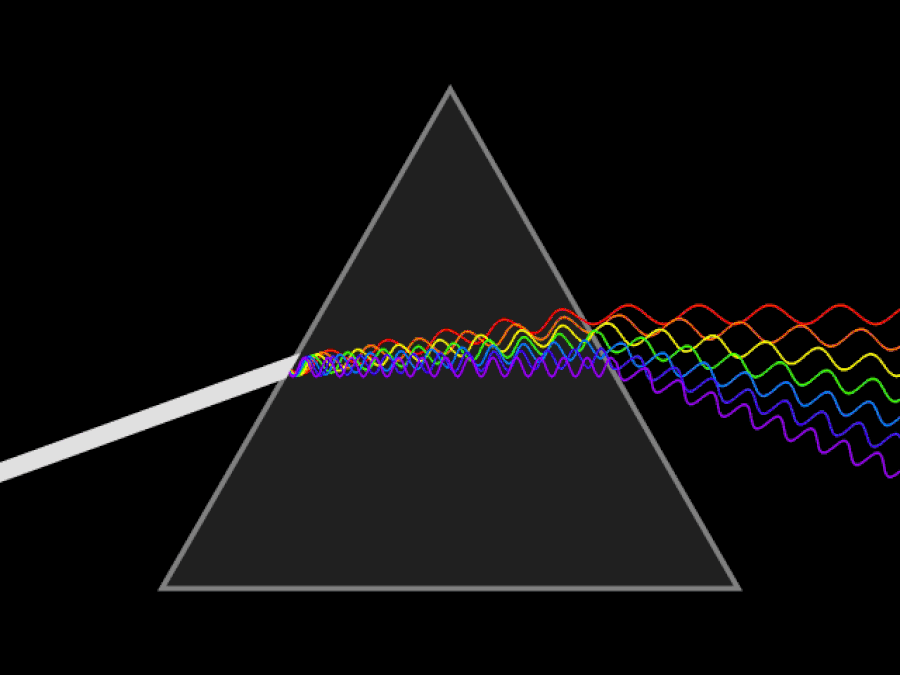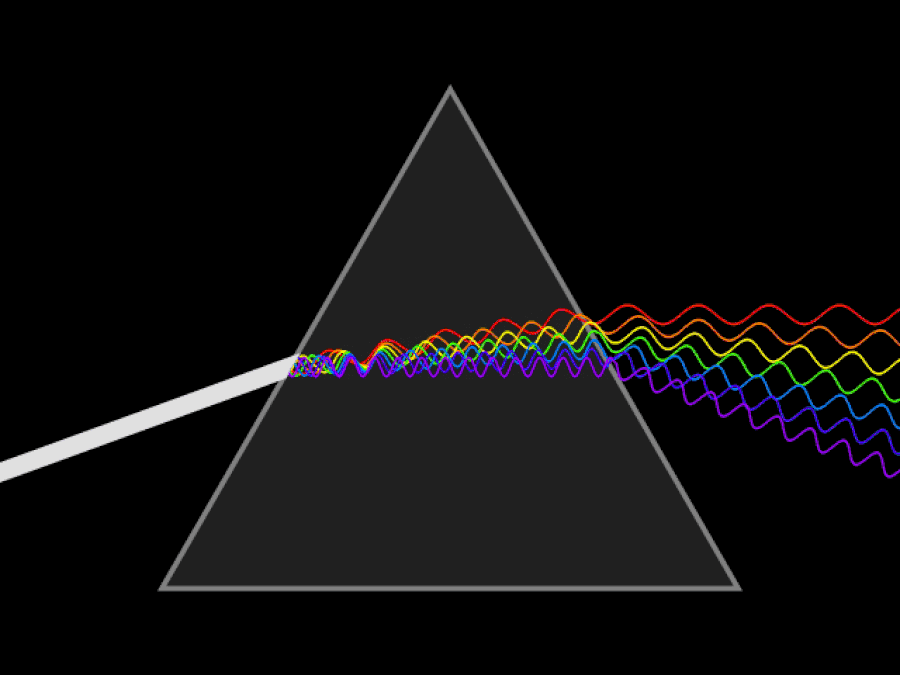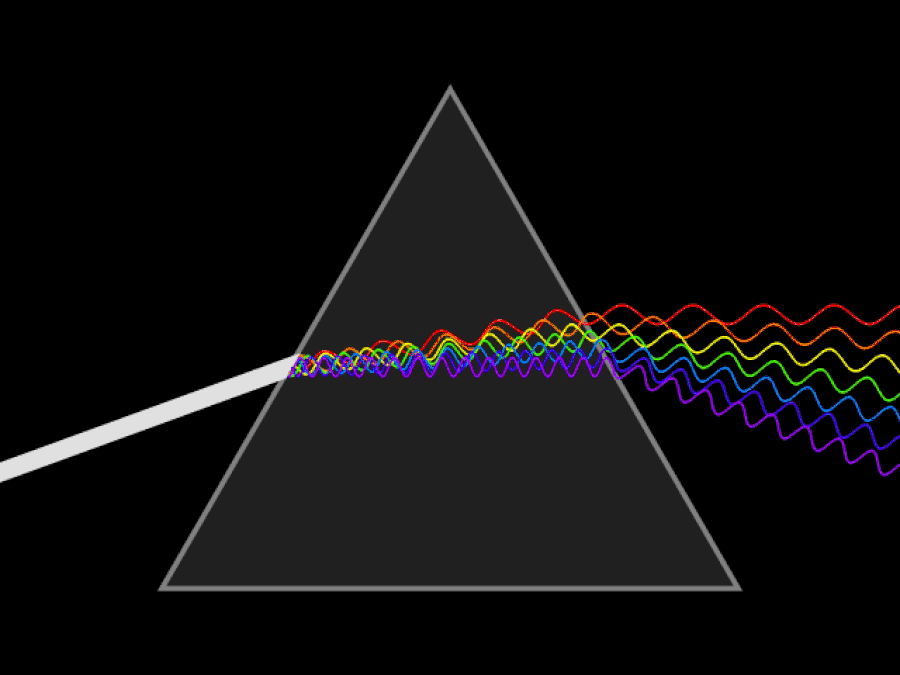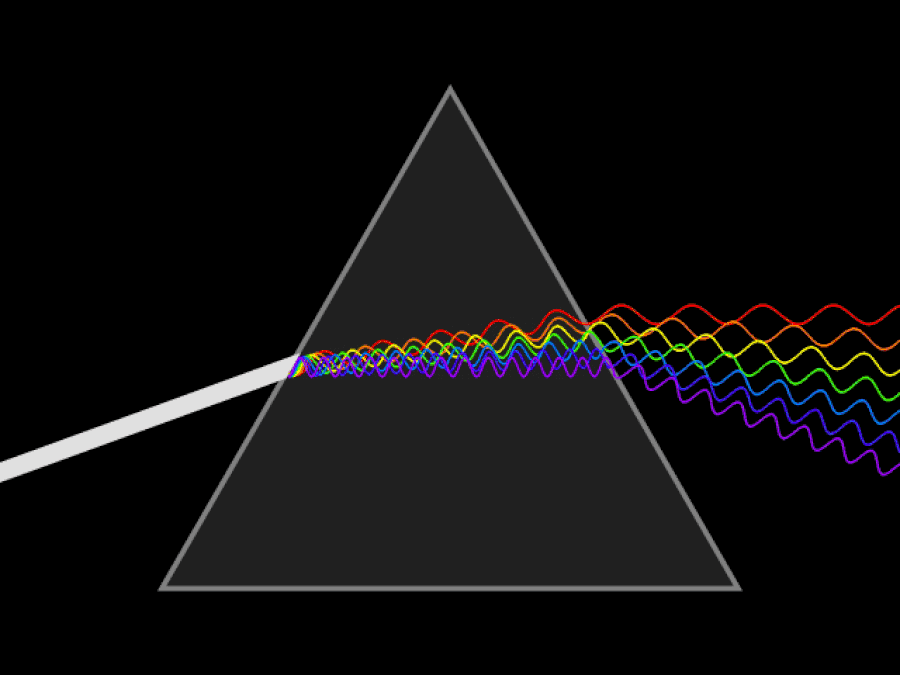
Think about what happens when you pass a beam of white light through a prism. Before that light enters the prism, all the different wavelengths — or colors of light — are propagating together. That’s why the light appears white: because it’s all the different wavelengths and colors all together. Each photon that makes up the white light has two properties: wavelength and frequency, where the wavelength is the distance between two successive “peaks” or “troughs” of light (i.e., the electromagnetic wave) and frequency is how many wavelengths-of-light are contained in each second of travel for the electromagnetic wave.
In the vacuum of empty space, the wavelength of light multiplied by the frequency of light always equals exactly the same value: the speed of light.
But when that light passes through a medium, it slows down. Through something like air, it only slows down by 0.03% or so, a completely negligible value. But through acrylic, it slows down by 33%; through zircon, it slows by 48%; through diamond, it slows by 59%. It also moves slower through water, slowing down by about 25% from its vacuum speed. And while the frequency of the light never changes, even as it moves through a medium, both its wavelength and its speed do.
Think about that for a second. The frequency of light cannot change, because if it did, it would violate the conservation of energy; the energy of a photon is just a constant (Planck’s constant) multiplied by the frequency, so if we want energy to be conserved (and physics mandates that), then the frequency cannot change. But the wavelength can change, and therefore so must the speed of each individual photon, or quantum of light.
But by how much? You might think it’s by the same exact amount, as I did just tell you earlier that light slows down by:
- 0.03% through air,
- 25% through water,
- 33% through acrylic,
- 48% through zircon, and
- 59% through diamond.
That’s true, but only on average. As it turns out, each individual medium slows light down by a slightly different amount, dependent on both wavelength and temperature. In general, “bluer” (or shorter-wavelength) light slows down by a little bit more than “redder” (or longer-wavelength) light, and hotter temperatures for your medium cause light to slow down by a little bit more than it does in a colder medium.
The fact that different wavelengths of light slow down by different amounts in a medium is what causes a prism, or any medium, to “disperse” colors.

It’s this physical effect that leads to the optical phenomenon of a rainbow. When sunlight, an example of white light, strikes a water drop, some of that light will actually enter the water for a time, slowing down, only to exit the water drop and have the light return back to normal speed. But the time it spent in that water drop causes the colors to separate, which is why you can shine sunlight through water and see color separation i.e., a rainbow effect when the light returns back into the air.
For the type of rainbow that you see when sunlight strikes rain, you have to remember two facts:
- that all of the Sun’s rays are parallel,
- and that water drops are roughly spherical.
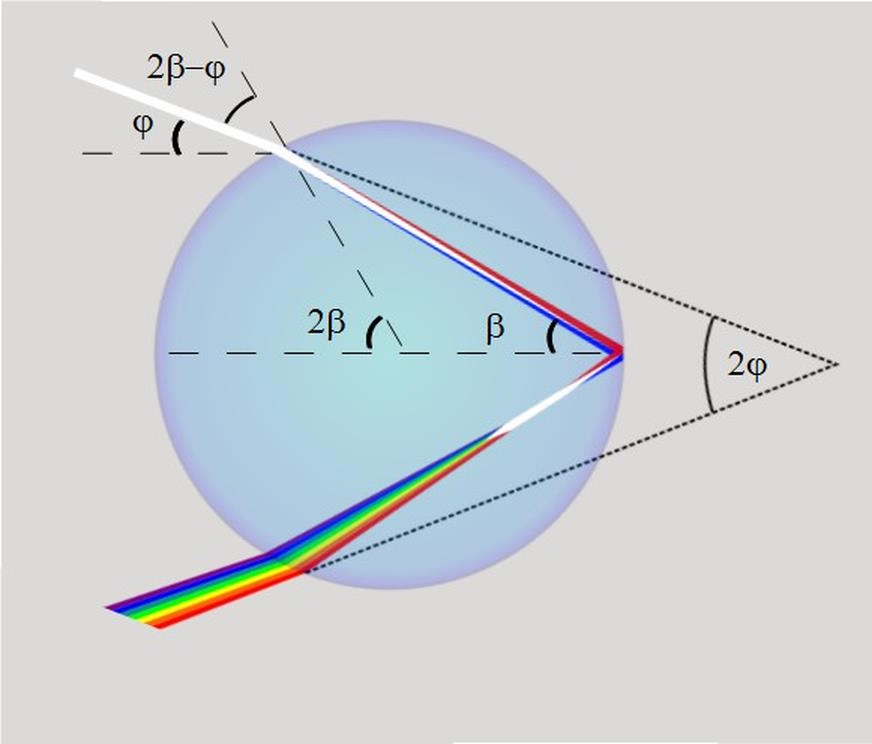
The rest is just geometry. When white light strikes a water drop at just the right angle, it won’t reflect off of the drop completely, but some of the light will refract, entering the drop and “splitting” the various wavelengths apart. When the light makes it to the back of the drop, it can reflect off of the back of the drop, causing the light to head back toward the Sun. But this time, when the light hits the water/air surface again, it moves from the water back into the air.
What’s remarkable is that because the geometry, the light, and the water are always the same, the light always makes the exact same set of angles: 42° for red light, 40° for violet light, with the full spectrum of colors between them. This was known nearly 400 years ago, and was illustrated in 1637 by René Descartes.
Think about what this means: the sunlight strikes the water, enters it, reflects once off of the back of the drop, and exits the drop. Red light always exits at a 42° angle; violet light always exits at a 40° angle, and the other colors fill in the spaces in between: in classic ROY-G-BIV order. With your back to the Sun, wherever those drops of water exist to form a rainbow, the shape and color of the rainbow will always be the same: at the exact same set of geometric angles, wherever these spherical drops of water exist to reflect the light.
In some cases, you won’t have intervening drops of water; these will appear as “gaps” in the rainbow. In some cases, when the Sun is quite high above the horizon, you can only see a tiny fraction of the arc close to the horizon; to the contrary, when the Sun is very low in the sky, you can see a full, large semicircle of a rainbow spanning an enormous swath of the sky. (In fact, if the Sun is more than 42° above the horizon, you won’t see a rainbow at all, because the geometry of the Sun-raindrop-observer system is all wrong.)
As a result, the most spectacular rainbows often appear very close to sunset, when large parts of the western horizon, where the Sun is setting, are clear, but where it’s raining over toward the east, where the Sun’s rays will reflect off of the drops.

If you’re on the surface of Earth, however, it’s usually impossible to see the true optical shape of a rainbow: a full circle, because there are only spherical drops of water in the atmosphere above the Earth’s surface, not down beneath the Earth’s surface, for the sunlight to reflect off of.
If you rise up above the surface of the Earth, however, such as in a hot air balloon, a blimp, or an airplane, however, this suddenly becomes possible as long as the Sun cooperates.
If you look in the opposite direction of the Sun, while airborne, there’s a “band” corresponding to the angles that are offset between 40° and 42° degrees from the imaginary line connecting the Sun to your eyes and beyond, to the horizon (or into the ground) in the opposite direction. Wherever there are spherical water drops for the sunlight to reflect off of in that band, you’ll see the corresponding component(s) of the full rainbow. And if you’re lucky enough that the entire 40°-42° band is filled with spherical water drops (i.e., raindrops) all the way around, from your perspective, you’ll have a chance to see the true shape of a rainbow: the illuminated full circle.

But don’t despair if you don’t have an airplane and the right conditions at your disposal; there’s a simpler and much more accessible way to see a full, circular rainbow. All you need is a sunny day and a garden hose capable of creating a wide, misty spray. The recipe is as follows:
- Stand with your back to the Sun.
- Point the garden hose so that it’s pointing at the shadow of your head on the ground.
- Open the hose so that the spray is wide and misty, and so that the spray particles extend for more than 42° away from your line-of-sight in all directions.
- Look at what happens.
- See the full-circle rainbow.
That’s it! With a little more sophistication, you can even construct a “sheet of rain” by having a large set of misting sprinklers set up with the right configuration to reflect the sunlight into the eye of the observer or camera lens. When the Sun’s rays reflect off of the droplets between 40° and 42° relative to the Sun-observer line and all get focused back into the observer’s field of vision all at once, a fully circular rainbow arises as a consequence of the science of optics. As long as there isn’t a brighter light source that washes any part of the rainbow out, you’ll be able to see the full circle yourself.

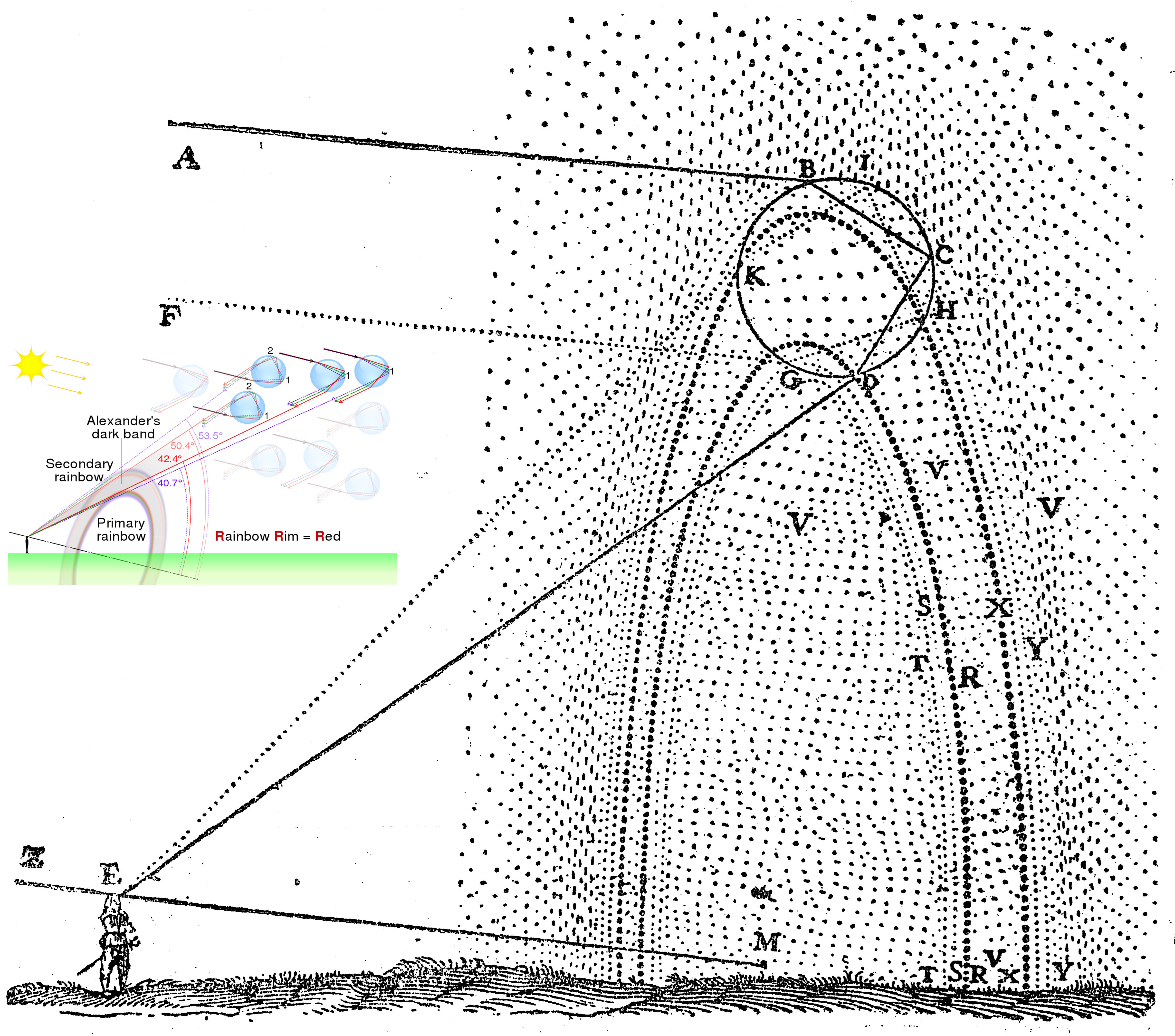
If you look closely, both at some of the photos above and also at the rainbows that appear in real life, you might notice a “secondary” rainbow outside of the primary rainbow: what’s sometimes known as a double rainbow when both are visible. The secondary rainbow arises from a different geometrical interaction of sunlight with spherical water drops: one where the sunlight enters, reflects off of the back of the drop, then reflects a second time off of the interior wall of the drop, and then exits the drop and returns to the air.
As a result, a fainter, color-order-reversed rainbow appears at a wider angle than the original rainbow: between 53.5° for the outer, violet layer and 50.4° for the inner, red layer, with the reversed-from-typical colors ordered VIB-G-YOR from the outside in.
Although you’d need the water droplets to extend farther out, it’s possible to recreate the same conditions as earlier either from an airplane or with a garden hose/mist system and see a full-circle double rainbow for yourself. This has been achieved before, and the documented photographic evidence is truly spectacular to behold.

It’s remarkable to realize that because rainbows aren’t physically real — they’re just optical phenomena, like shadows — that if you could simply add more “mist particles” for the sunlight to reflect off of in the right locations, you’d be able to see the true shape of a rainbow every time: a full circle, with an inner (violet) angular radius of 40° and an outer (red) angular radius of 42°. Similarly, a color-reversed, fainter secondary full-circle rainbow always exists as well, with an inner (red) angular radius of 50.4° and an outer (violet) radius of 53.5°. Wherever you can recreate these conditions, you’ll be able to see the full rainbows in all their glory.
In fact, fainter and fainter rainbows exist, with a new set of angles determined solely by geometry, with each new internal reflection that you add. The tertiary (three-reflection) and quaternary (four-reflection) rainbows are in the sunward direction, so human eyes are terrible at seeing them, but the quinary (five-reflection) rainbow actually falls in between the primary and secondary rainbow, and was photographed for the first time by humans back in 2014. In laboratory conditions, up to 200th-order rainbows have been detected, and just as you’d expect: they’re all full circles.
The next time you see a rainbow, used your imagination to try and trace out the full circle that you know it needs to be. You just might be impressed by how remarkably large the true extent of a rainbow actually is!





