How the best alternative to “quantum spookiness” failed

For all of history, there’s been an underlying but unspoken assumption about the laws that govern the Universe: If you know enough information about a system, you can predict precisely how that system will behave in the future. The assumption is, in other words, deterministic. The classical equations of motion — Newton’s laws — are completely deterministic. The laws of gravity, both Newton’s and Einstein’s, are deterministic. Even Maxwell’s equations, governing electricity and magnetism, are 100% deterministic as well.

But that picture of the Universe got turned on its head with a series of discoveries that began in the late 1800s. Starting with radioactivity and radioactive decay, humanity slowly uncovered the quantum nature of reality, casting doubt on the idea that we live in a deterministic Universe. Predictively, many aspects of reality could only be discussed in a statistical fashion: where a set of probable outcomes could be presented, but which one would occur, and when, could not be precisely established. The hopes of avoiding the necessity of “quantum spookiness” was championed by many, including Einstein, with the most compelling alternative to determinism put forth by Louis de Broglie and David Bohm. Decades later, Bohmian mechanics was finally put to an experimental test, where it failed spectacularly. Here’s how the best alternative to the spooky nature of reality simply didn’t hold up.

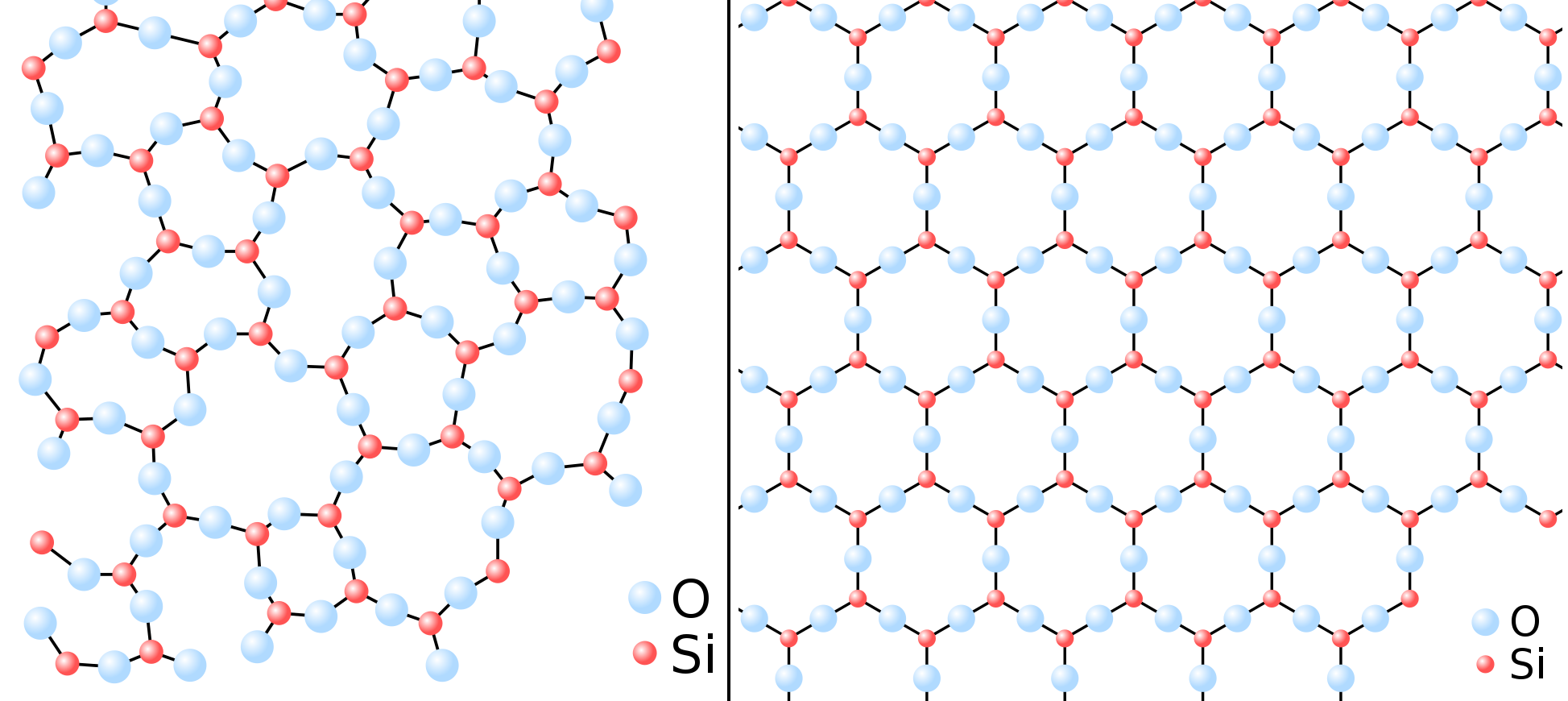
Perhaps the spookiest of all quantum experiments is the double-slit experiment. When a particle passes through the double slit, it will land in a region whose probabilities are defined by an interference pattern. With many such observations plotted together, the interference pattern can be seen if the experiment is performed properly. (Credit: Thierry Dugnolle/Wikimedia Commons)

There are all sorts of experiments we can perform that illustrate the indeterminate nature of our quantum reality.

• Place a number of radioactive atoms in a container and wait a specific amount of time. When you observe your container at that later time, you can predict how many atoms remain versus how many have decayed, on average, but you cannot predict which ones will decay versus which ones will remain at all.
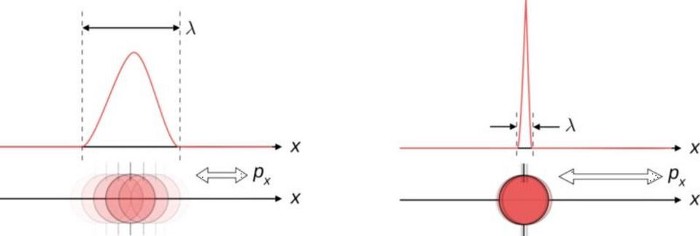
• Fire a series of particles through a narrowly spaced double slit and you’ll be able to predict what sort of interference pattern will arise on the screen behind it. However, for each and every particle, even when you’re capable of sending them through the slits one at a time, you cannot predict — other than purely probabilistically — where each one will land.
• Pass a series of particles (that possess quantum spin) through a magnetic field and watch half of them deflect “up” and half “down” in the direction of the field. If you pass them through another magnet oriented the same way, the ones that went “up” will still go “up” and the ones that went “down” still go down, unless you pass them through an in-between magnet oriented in one of the two perpendicular directions. If you do, the beam will split again and the particles’ spins in the original direction will be re-randomized once again, with no way to determine which way they’ll split when you pass them through the final magnet.

When a particle with quantum spin is passed through a directional magnet, it will split in at least 2 directions, dependent on spin orientation. If another magnet is set up in the same direction, no further split will ensue. However, if a third magnet is inserted between the two in a perpendicular direction, not only will the particles split in the new direction, but the information you had obtained about the original direction gets destroyed, leaving the particles to split again when they pass through the final magnet. 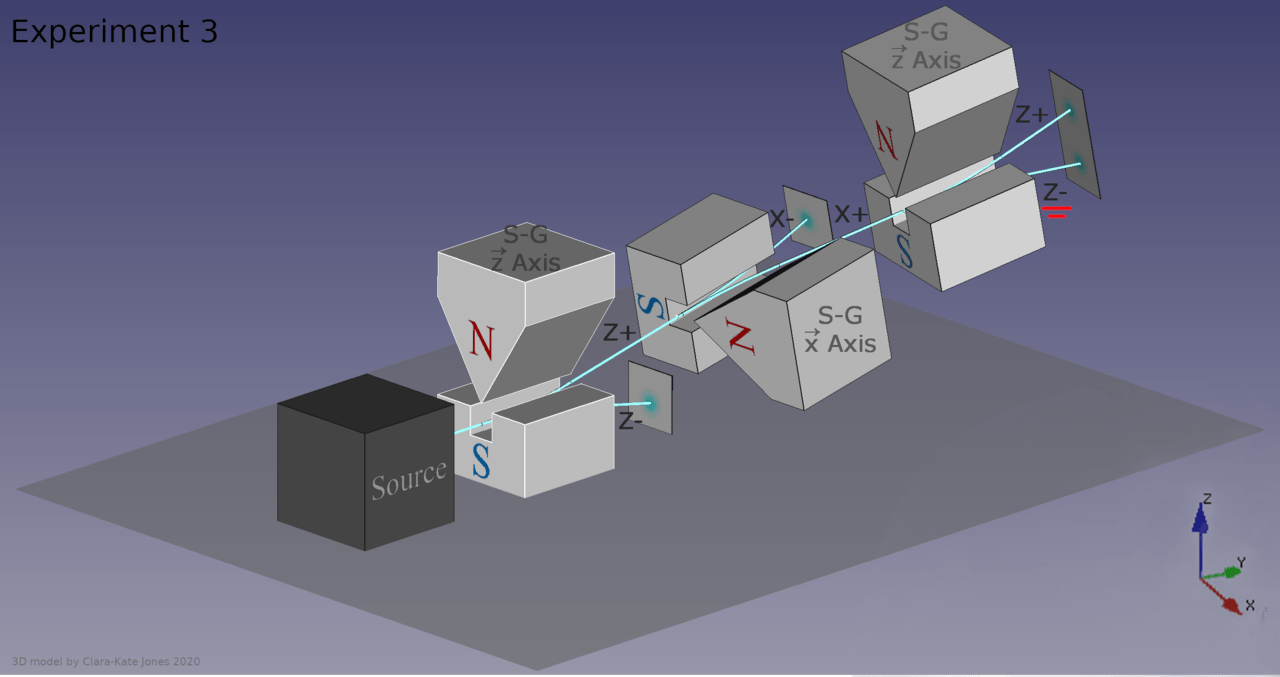(Credit: MJasK/Wikimedia Commons)

The list of experiments that display this sort of quantum weirdness or spookiness is long, and these examples are far from exhaustive. This inherently quantum behavior shows up in all sorts of physical systems, both for individual particles and for complex systems of particles as well, under a variety of conditions. Although physicists have been able to write down the rules and equations that govern these quantum systems, including the Pauli Exclusion Principle, the Heisenberg Uncertainty Principle, the Schrodinger equation and many more, the fact is that only a set of conditions and probable outcomes can be predicted in the absence of a measurement.

Somehow, in quantum systems, the act of making a measurement appeared to be a very important factor, flying in the face of the idea that we inhabited a sort of “independent reality” that was observer-independent. Properties of a physical system that had previously been treated as intrinsic and immutable — like position, momentum, angular momentum, or even the energy of a particle — were suddenly knowable only up to a certain precision. Moreover, the act of measuring those properties, which required an interaction with another quantum of some type, fundamentally changes, or perhaps even determines, those values, while simultaneously increasing the indeterminism and/or uncertainties of other measurable parameters.

This diagram illustrates the inherent uncertainty relation between position and momentum. When one is known more accurately, the other is inherently less able to be known accurately. Every time you accurately measure one, you ensure a greater uncertainty in the corresponding complementary quantity. (Credit: Maschen/Wikimedia Commons)

The central idea behind what we now call the Copenhagen Interpretation of quantum mechanics, which is the standard way that physics students are taught to conceive of the quantum Universe, is that nothing is certain until that critical moment where an observation occurs. Everything that cannot be exactly calculated from what’s already known is describable by some sort of wavefunction — a wave that encodes a continuum of more likely and less likely possible outcomes — until the critical moment when a measurement is made. At that precise instant, the wavefunction description gets replaced by a single, now-determined reality: what some describe as a collapse of the wavefunction.

It was this level of weirdness, or “spookiness,” that was so objectionable to many. Einstein was perhaps the most famous. He was aghast at the idea that somehow reality was random in nature, and that effects could occur — like one member of a pair of identical atoms decaying while the other did not — without an identifiable cause. In many ways, this position was summed up in a famous remark attributed to Einstein, “God does not play dice with the Universe.” While Einstein himself never came up with an alternative, one of his (and Bohr’s) contemporaries had an idea for how reality could work instead: Louis de Broglie.

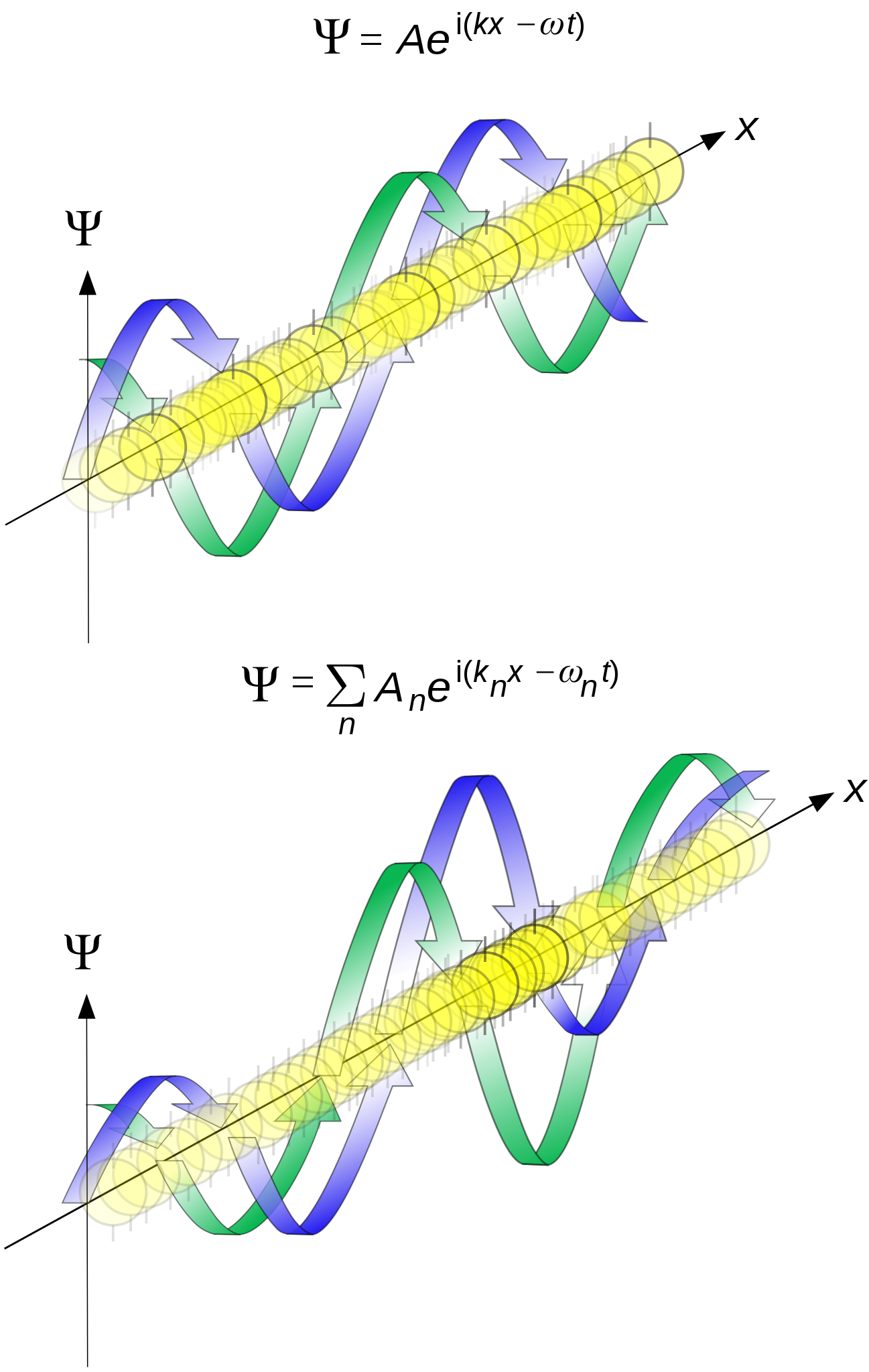
The idea of a de Broglie wave is that every matter particle can also exhibit wavelike behavior, with the properties of the wave given by quantities like momentum and energy of the system. Everything, from electrons to human beings, behave like a wave under the proper conditions. (Credit: Maschen/Wikimedia Commons)

In the early days of quantum mechanics, de Broglie gained fame for showing that it wasn’t simply light that possessed a dual nature of being simultaneously wave-like and particle-like, but that matter itself possesses a wave-like nature when subjected to the proper quantum conditions. His formula for calculating the wavelength of “matter waves” is still widely used today, and to de Broglie, it’s because we ought to be taking the dual nature of quanta literally.

In de Broglie’s version of quantum physics, there were always concrete particles, with definite (but not always well-measured) positions to them, that are guided through space by these quantum mechanical wavefunctions, which he called “pilot waves.” Although de Broglie’s version of quantum physics couldn’t describe systems with more than one particle, and suffered from the challenge of not being able to measure or identify precisely what was “physical” about the pilot wave, it represented an interesting alternative to the Copenhagen interpretation.

Instead of being governed by the weird rules of quantum spookiness, there was an underlying, hidden reality that was completely deterministic. Many of de Broglie’s ideas were expanded upon by other researchers, who all sought to discover a less “spooky” alternative to the quantum reality that generations of students, with no superior alternative, had been compelled to accept.

This generic illustration of quantum tunneling assumes there is a high, thin, but finite barrier separating a quantum wavefunction on one side of the x-axis from the other. While most of the wavefunction, and hence the probability of the field/particle that it’s a proxy for, reflects and remains on the original side, there is a finite, non-zero probability of tunneling through to the other side of the barrier. This phenomenon must be explicable in all interpretations of quantum mechanics. (Credit: Yuvalr/Wikimedia Commons)

Perhaps the most famous extension came courtesy of the physicist David Bohm, who in the 1950s developed his own interpretation of quantum physics: the de Broglie-Bohm (or pilot wave) theory. The underlying wave equation, in this idea, is the same as the conventional Schrodinger equation, as in the Copenhagen interpretation. However, there’s also a guiding equation that acts on the wavefunction, and properties like the position of a particle can be extracted from the relationship of that guiding equation. It’s an explicitly causal, deterministic interpretation, with a fundamental non-locality to it.

But this interpretation posed its own difficulties. For one, you can’t recover classical dynamics using this pilot wave theory; Newton’s F = ma doesn’t describe the dynamics of a particle at all. In fact, the particle itself doesn’t affect the wavefunction in any way; rather, the wavefunction describes the velocity field of each particle or system of particles, and you have to apply the appropriate “guiding equation” to find out just where the particle is and how its motion is affected by whatever is exerting a force on it.

When a ball floats upon a river, its path will follow the river’s current, but its inertia will also determine its trajectory. As a result, it will normally take only a short amount of time before it winds up on one of the water’s banks: close to the shore. (Credit: pxfuel)

In many ways, pilot wave theory was more of an interesting counterexample to the assertion that “no hidden variable theory could reproduce the success of quantum indeterminism.” It could, as Bohm’s pilot wave theory illustrated, but at the cost of a fundamental non-locality and the difficult notion of having to extract physical properties from a guiding equation, whose results are not necessarily straightforward to work with.

Consider the following example: a particle, like a ball, floating on top of a flowing river. In Newtonian mechanics, what happens to the ball is simple: The ball has a mass, which means it has an inertia, and that means it follows Newton’s first and second laws. This object in motion will remain in motion unless acted on by an outside force. If it is acted upon by an outside force, it accelerates via that famous equation, F = ma. As the ball travels downstream, the river’s twists and turns will cause the water to flow downstream, but will quickly drive the ball to one bank of the river or the other. Inertia is the guiding principle behind the floating ball’s motion.

But in Bohmian mechanics, the flow of the river determines the evolution of the wavefunction, which should preferentially stay in the center of the river. This shows the conceptual difficulty with pilot wave theory: If you want your particle to ride on the wavefunction like a surfer — as de Broglie originally envisioned — you have to go through a variety of twisted contortions to get back the basic predictions that we’re all familiar with from classical mechanics.

As an alternative to quantum weirdness or spookiness, where a quantum behaves wave-like until you measure it, upon where it behaves like a particle, the pilot wave interpretation claims that the particle is like a “surfer” atop the “waves” that underlie the system. However, any interpretation making these claims must agree with experiments: a tall order. (Credit: Dan Harris/MIT)

As the perfectly valid Copenhagen interpretation has long demonstrated, however, just because something is counterintuitive or even illogical doesn’t mean it’s incorrect. Physical behavior is often more bizarre than we’d ever expect, and that is why we must always confront our predictions with the harsh reality of experiments.

In 2006, physicists Yves Couder and Emmanuel Fort began to bounce an oil droplet atop a vibrating fluid bath made out of that same oil, recreating the analogue of the quantum double-slit experiment. As the wave ripples down the tank and approaches the two slits, the droplet bounces atop the waves and is guided through one slit or the other by the waves. When many droplets were passed through the slits and a statistical pattern emerged, it was found to exactly reproduce the standard predictions of quantum mechanics.

In 2013, an expanded team led by John Bush at MIT leveraged the same technique to test a different quantum system: confining electrons into a circular corral-like area by a ring of ions. To the surprise of many, with an appropriately set up boundary, the underlying wave patterns that are produced are complex, but the trajectory of the bouncing droplet(s) atop them do, in fact, follow a pattern determined by the wavelength of the waves, in agreement with the quantum predictions that underlie them.

Surface waves with a bouncing droplet confined in a circular area reflect back on one another, producing ripples that steer the droplet in a non-random trajectory that possesses many of the aspects of quantum mechanics. (Credit: Dan Harris/MIT)

What appeared to be random, in these experiments, wasn’t truly random at all, but rather provided a thrilling confirmation of the ideas of pilot wave theory.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

And then it all fell apart.

Normally, the double slit experiment only gives you the vaunted interference pattern if you don’t measure which of the two slits the particle passes through. At quantum scales, setting up a detector at the slits themselves tells you which slit each particle goes through, but destroys the interference pattern. You simply get two piles of particles on the other side, with each pile corresponding to one of the two slits.

In Couder and Fort’s original 2006 experiment, they had set 75 separate bouncing droplets through the slits where they could watch which slit each droplet passed through — while also recorded the pattern of where they landed on the screen — finding the needed interference pattern. If this held up, it would seem to confirm that, perhaps, there really could be these hidden variables underlying what appeared to be an indeterminate quantum reality.

And then the reproduction attempts came. Lo and behold, as soon as the path through one of the two slits was singled out by each droplet, the paths that the particle takes depart from what quantum mechanics predicts. There was no interference pattern, and it was found that the original work contained a few mistakes that were corrected in the reproduction attempt. As the authors of the 2015 study refuting Couder and Fort’s work conclude:

“We show that the ensuing particle-wave dynamics can capture some characteristics of quantum mechanics such as orbital quantization. However, the particle-wave dynamics can not reproduce quantum mechanics in general, and we show that the single-particle statistics for our model in a double-slit experiment with an additional splitter plate differs qualitatively from that of quantum mechanics.”

A vibrating oil surface with a droplet bouncing upon it will appear to reproduce a number of aspects of quantum mechanics, but was shown to display fundamental differences to the true quantum theory. The double-slit experiment, importantly, cannot be reproduced by this quantum analogue system. (Credit: A. Andersen et al., Phys. Rev. E, 2015)

Of course, arguing over whether reality is truly acausal, truly indeterminate, or lacking any hidden variables is tantamount to playing a never-ending game of whack-a-mole. Any specific claim that can be tested can always be ruled out, but it can be replaced with a more complex, hitherto untestable claim that still purports to have whatever aspects (or combination of aspects) one desires. Still, when assembling our picture of reality, it’s important to make sure that we don’t ideologically choose one that conflicts with the experiments we can perform.

We may not have the ultimate “right answer” to the question of how the Universe works, but we have knocked down a tremendous number of pretenders from the throne. If your predictions disagree with experiments, your theory is wrong, no matter how popular or pretty it happens to be. We have not yet ruled out all possible incarnations of Bohmian mechanics, or pilot wave theories, or quantum mechanics interpretations that have hidden variables. It may not ever be possible to do so. However, every attempt to construct a theory that agrees with experiment requires some level of quantum spookiness that simply cannot be done away with. The least spooky alternative has now been falsified, as a single, concrete reality cannot describe all that we observe and measure.