The Universe’s most unbreakable symmetry

The ultimate goal of physics is to accurately describe, as precisely as possible, exactly how every physical system that can exist in our Universe will behave. The laws of physics need to apply universally: the same rules must work for all particles and fields in all locations at all times. They must be good enough so that, no matter what conditions exist or what experiments we perform, our theoretical predictions match the measured outcomes. And having predictive power, explicitly, means that if you know the initial conditions of your system and the laws that govern it, you can predict what the outcomes — or the relative probability of the set of possible outcomes — will always turn out to be.

The most successful physical theories of all are twofold:

• the quantum field theories that describe each of the fundamental interactions that occur between particles,
• as well as General Relativity, which describes spacetime and gravitation.

And yet, there’s one fundamental symmetry that applies to not just all of these physical laws, but for all physical phenomena: CPT symmetry. And for nearly 70 years, we’ve known of the theorem that forbids us from violating it.

There are many letters of the alphabet that exhibit particular symmetries. Note that the capital letters shown here have one and only one line of symmetry; letters like “H”, “I”, “O” and “X” have more than one. This ‘mirror’ symmetry, known as Parity (or P-symmetry), has been verified to hold for all strong, electromagnetic, and gravitational interactions wherever tested. However, the weak interactions offered a possibility of Parity violation. The discovery and confirmation of this was worth the 1957 Nobel Prize in Physics.

For most of us, when we hear the word symmetry, we think about reflecting things in a mirror. Some of the letters of our alphabet exhibit this type of symmetry: “A” and “T” are vertically symmetric, while “B” and “E” are horizontally symmetric. “O” is symmetric about any straight line that goes through its central point, as well as possessing rotational symmetry: no matter how you rotate it, its appearance is unchanged. These symmetries — known as “line” symmetry and “point” symmetry, respectively — are the two symmetries we have the most experience with in our day-to-day lives.

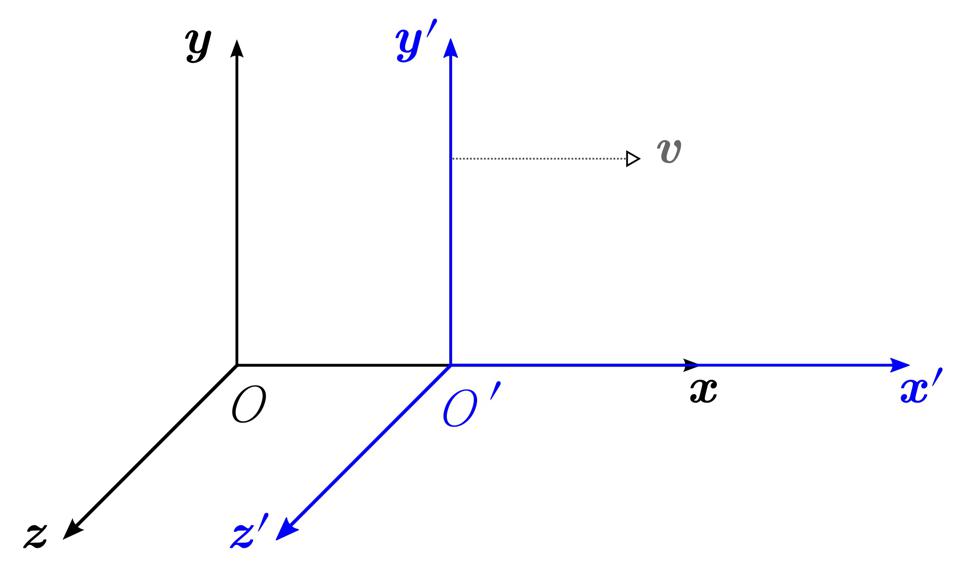
But there are other kinds of symmetry that show up in nature as well. If you have a horizontal line and you shift that line by any amount in the horizontal line, it remains unchanged: it’s still the the same horizontal line. That’s an example of what we call “translational” symmetry. If you’re inside a train car and the experiments you perform give the same outcome whether the train is at rest or moving quickly down the track, that’s a symmetry under boosts (or velocity transformations). Some of these common symmetries always hold under the known physical laws, while others are only valid sometimes: so long as certain conditions are met.

Different frames of reference, including different positions and motions, would see different laws of physics (and would disagree on reality) if a theory is not relativistically invariant. The fact that we have a symmetry under ‘boosts,’ or velocity transformations, tells us we have a conserved quantity: linear momentum. The fact that a theory is invariant under any sort of coordinate or velocity transformation is known as Lorentz invariance, and any Lorentz invariant symmetry conserves CPT symmetry. However, C, P, and T (as well as the combinations CP, CT, and PT) may all be violated individually. The original formulations of quantum mechanics did not have this property.

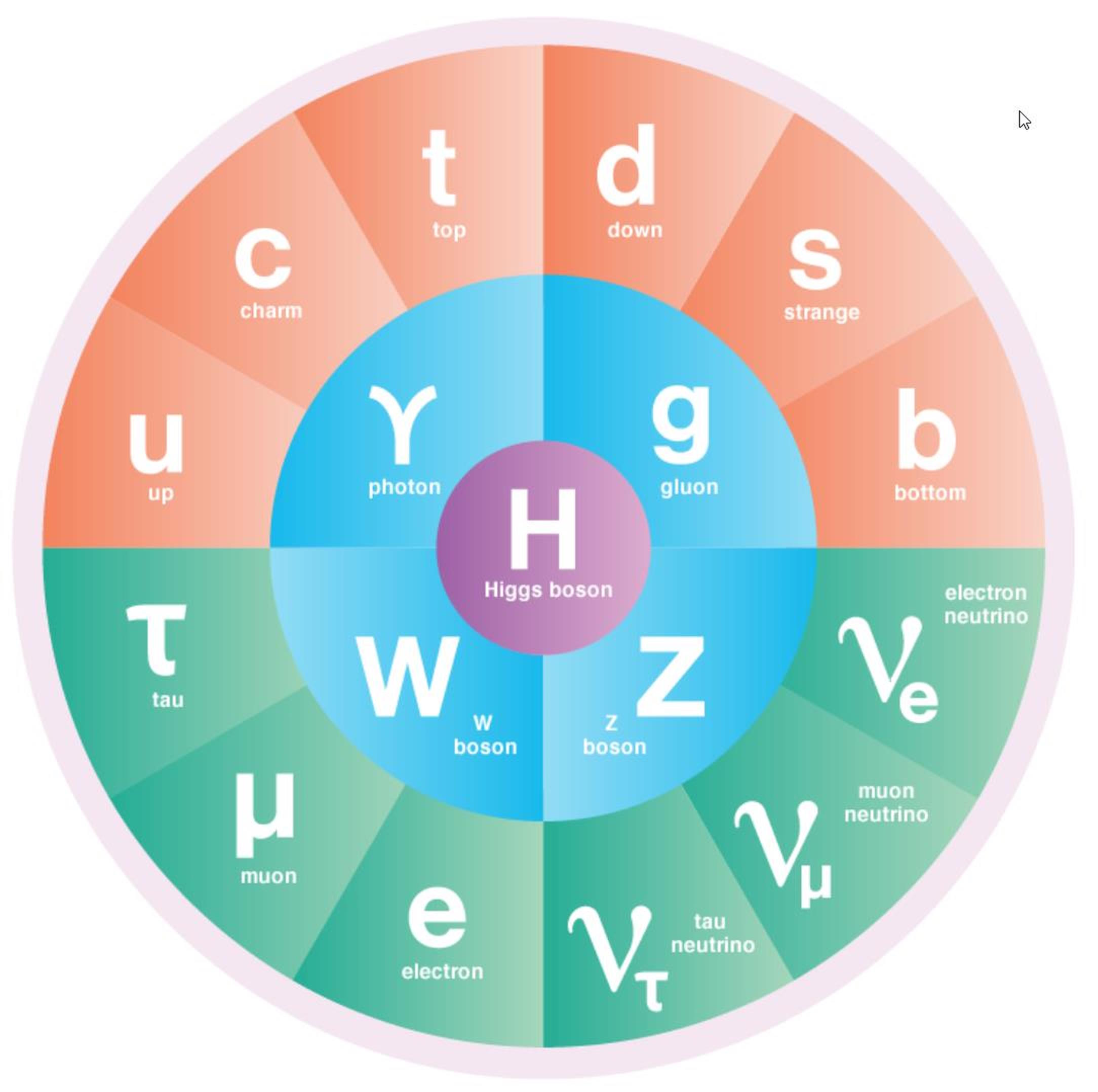
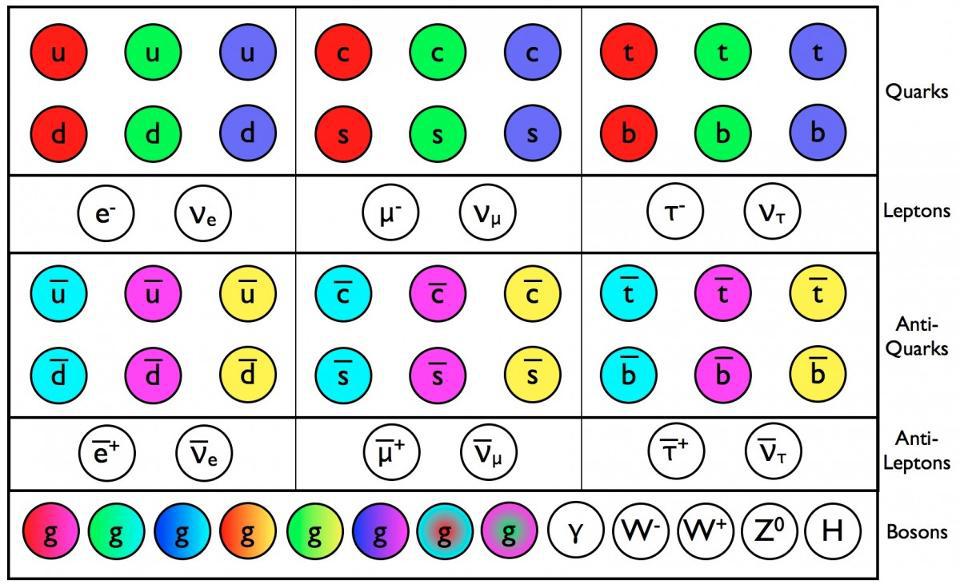
If we want to go down to a fundamental level, and consider the smallest indivisible particles that make up everything we know of in our Universe, that would lead us to take a look at the particles of the Standard Model. Consisting of the fermions (quarks and leptons) and bosons (gluons, photon, W-and-Z bosons, and the Higgs), these comprise all of the particles we know of that make up the matter and radiation we’ve directly performed experiments on in the Universe. (Although we also have strong evidence that dark matter and dark energy exist, they are not included in this picture, and cannot be accounted for by any of the known Standard Model particles.)

Under the laws of both Quantum Field theory and General Relativity, we can calculate the forces between any particles in any configuration, and determine how they’ll move, interact, and evolve over time. We can observe how matter particles behave under the same conditions as antimatter particles and determine where their behavior is identical to one another and where they’re different from each other. We can perform experiments that are the mirror-image counterparts of other experiments, and note the results. All three of these test the validity of various symmetries.

According to the Standard Model, the leptons and antileptons should all be separate, independent particles from one another. But the three types of neutrino all mix together, indicating they must be massive and, furthermore, that neutrinos and antineutrinos may in fact be the same particle as one another: Majorana fermions.

In physics, these three fundamental symmetries — the symmetries between matter and antimatter, the symmetries between systems of particles and their mirror-image reflections, and the symmetry of running the clock either forward or backward — have specific names and rules that they follow.

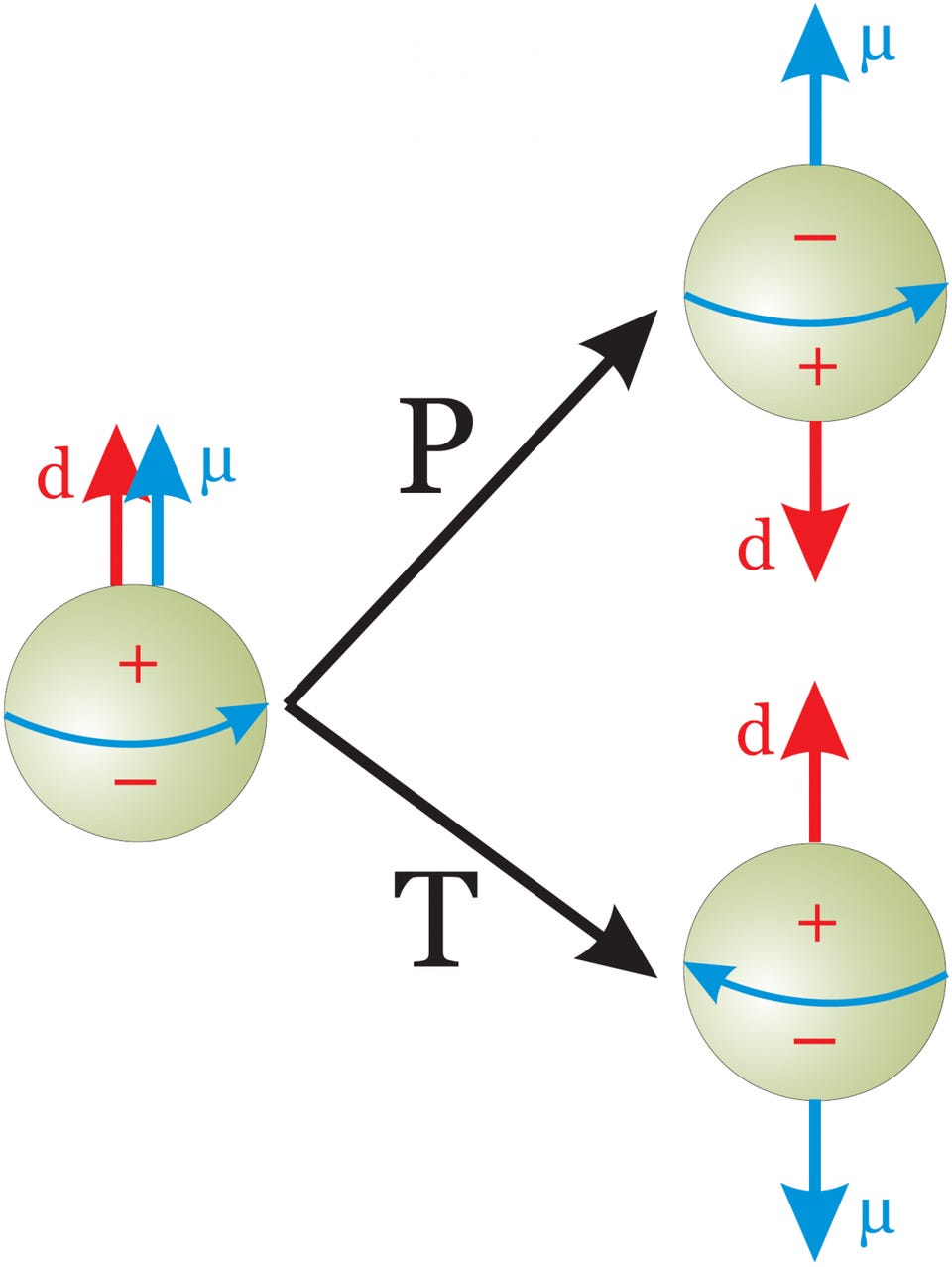
1. Charge conjugation (C): this symmetry involves replacing every particle in your system with its antimatter counterpart. It’s called charge conjugation because every charged particle has an opposite charge (such as electric or color charge) for its corresponding antiparticle.
2. Parity (P): this symmetry involves replacing every particle, interaction, and decay with its mirror-image counterpart.
3. Time-reversal symmetry (T): this symmetry mandates that the laws of physics affecting the interactions of particles behave the exact same ways whether you run the clock forward or backward in time.

Most of the forces and interactions that we’re used to obey each of these three symmetries independently. If you threw a ball in the gravitational field of Earth and it made a parabola-like shape, it wouldn’t matter if you replaced the particles with antiparticles (C), it wouldn’t matter if you reflected your parabola in a mirror or not (P), and it wouldn’t matter if you ran the clock forward or backward (T), so long as you ignored things like air resistance and any (not-perfectly-elastic) collisions with the ground.

A ball in mid-bounce has its past and future trajectories determined by the laws of physics, but time will only flow into the future for us. If there were no air resistance and no loss-of-energy whenever the ball struck the ground, an observer would not be able to tell whether the ball started on the left and moved to the right as time went forward, or vice versa. While Newton’s laws of motion are the same whether you run the clock forward or backward in time, as well as being left-right symmetric and matter-antimatter symmetric, not all of the rules of physics behave identically under all of these symmetries.

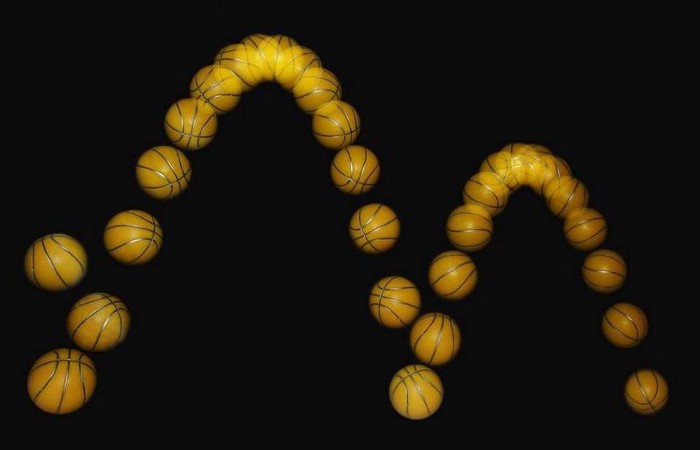
But individual particles don’t obey all of these symmetries under all of the physical conditions that we can imagine. Some particles have been observed to behave in a fundamentally different way than their antiparticles, violating C-symmetry. Neutrinos and antineutrinos — at least, the ones that can be observed — are always seen to be in motion and moving close to the speed of light. However, if you point your left thumb in the direction that the particles move, the neutrinos always “spin” in the direction that your fingers on your left hand curl in around the neutrino, while antineutrinos are always “right-handed” in the same fashion.

Some particles are unstable and will decay given enough time, and some of those particle decays violate parity. If you have an unstable particle that spins in one direction and then decays, its decay products can be either aligned or anti-aligned with the spin. If the unstable particle exhibits a preferred directionality to its decay, then the mirror image decay will exhibit the opposite directionality, violating P-symmetry.

Nature is not symmetric between particles/antiparticles or between mirror images of particles. (Or, for that matter, both mirror reflection and charge conjugation symmetry combined.) Prior to the detection of neutrinos, which clearly violate mirror-symmetries even without decays, as all neutrinos are left-handed and all anti-neutrinos are right-handed, weakly decaying particles offered the only potential path for identifying P-symmetry violations.

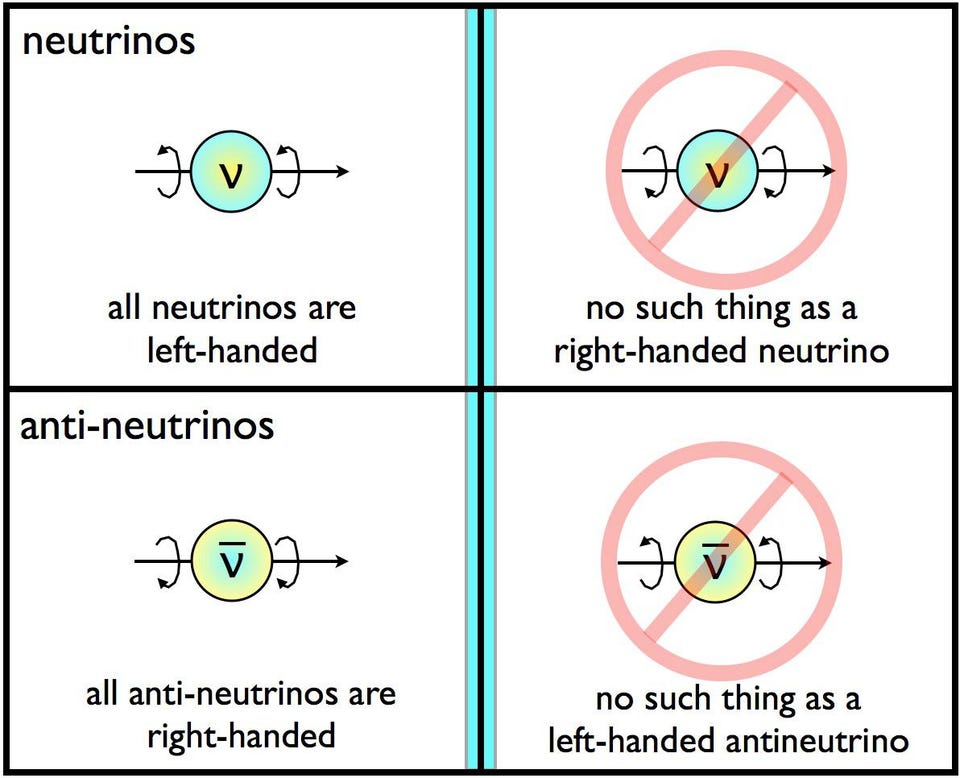
You can test the combination of these symmetries as well, by setting up the mirror-image of your system and then replacing the particles in the mirror with antiparticles. That combination, which can either be violated or conserved, is known as CP-symmetry.

In the 1950s and 1960s, a series of experiments were performed that tested each of these symmetries and how well they performed under the gravitational, electromagnetic, strong and weak nuclear forces. Under the strong nuclear force, as well as under the electromagnetic and gravitational forces, no such symmetry violations were observed. This remains true even all the way up into the present day; as of the 2020s, no violations of either C, P, or T symmetry have ever been seen.

Perhaps surprisingly, however, the weak interactions were observed to violate each of the C, P, and T symmetries individually, as well as combinations of any two such symmetries (CP, PT, and CT) together.

These violations are important for our understanding of the Universe, to be certain. But all of the fundamental interactions, every single one, always obey the combination of all three of these symmetries together: CPT symmetry.

Parity, or mirror-symmetry, is one of the three fundamental symmetries in the Universe, along with time-reversal and charge-conjugation symmetry. If particles spin in one direction and decay along a particular axis, then flipping them in the mirror should mean they can spin in the opposite direction and decay along the same axis. This was observed not to be the case for the weak decays, which are the only interactions known to violate charge-conjugation (C) symmetry, parity (P) symmetry, and the combination (CP) of those two symmetries as well.

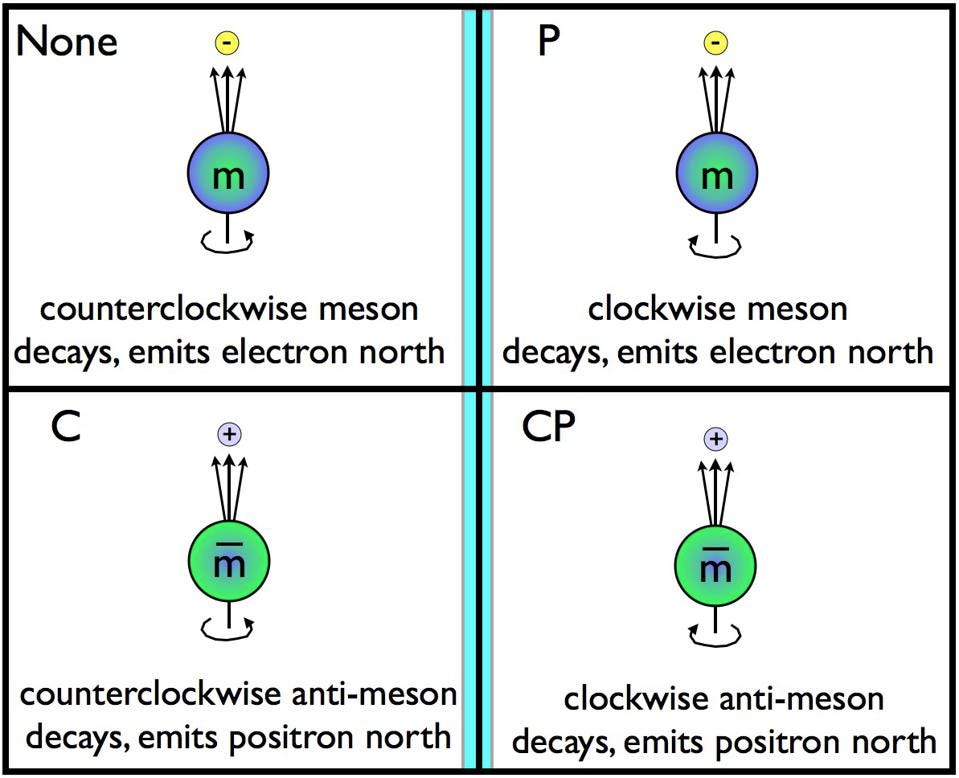
CPT symmetry says that any physical system made of particles that moves forward in time will obey the same laws as the identical physical system made of antiparticles, reflected in a mirror, that moves backward in time. It’s an observed, exact symmetry of nature at the fundamental level, and it should hold for all physical phenomena, even ones we have yet to discover.

On the experimental front, particle physics experiments have been operating for decades to search for violations of CPT symmetry. To significantly better precisions than 1-part-in-10-billion, CPT is observed to be a good symmetry in meson (quark-antiquark), baryon (proton-antiproton), and lepton (electron-positron) systems. Not a single experiment has ever observed an inconsistency with CPT symmetry, and that’s a good thing for the Standard Model.

It’s also an important consideration from a theoretical perspective, because there’s a CPT theorem that demands that this combination of symmetries, applied together, must not be violated. Although it was first proven in 1951 by Julian Schwinger, there are many fascinating consequences that arise because of the fact that CPT symmetry must be conserved in our Universe, and numerous pathologies that would show up were it to be fundamentally violated.

We can imagine that there’s a mirror Universe to ours where the same rules apply. If the big red particle pictured above is a particle with an orientation with its momentum in one direction, and it decays (white indicators) through either the strong, electromagnetic, or weak interactions, producing ‘daughter’ particles when they do, that is the same as the mirror process of its antiparticle with its momentum reversed (i.e., moving backward in time). If the mirror reflection under all three (C, P, and T) symmetries behaves the same as the particle in our Universe, then CPT symmetry is conserved.

The first consequence is that our Universe as we know it would be indistinguishable from a specific incarnation of an anti-Universe. If you were to change:

• the position of every particle to a position that corresponded to a reflection through a point (P reversal),
• each and every particle replaced by their antimatter counterpart (C reversal),
• and the momentum of each particle reversed, with the same magnitude and opposite direction, from its present value (T reversal),

then that anti-Universe would evolve according to exactly the same physical laws as our own Universe.

Another consequence is that if the combination of CPT holds, then every violation of one of them (C, P, or T) must correspond to an equivalent violation of the other two combined (PT, CT, or CP, respectively) in order to conserve the combination of CPT. It’s why we knew that T-violation needed to occur in certain systems decades before we were capable of measuring it directly: because the observed CP violation demanded it be so. It also means that as soon as we measure C-violation and P-violation, we instantly knew that PT-symmetry and CT-symmetry would need to be violated as well.

In the Standard Model, the neutron’s electric dipole moment is predicted to be a factor of ten billion larger than our observational limits show. The only explanation is that somehow, something beyond the Standard Model is protecting this CP symmetry in the strong interactions. If C is violated, so is PT; if P is violated, so is CT; if T is violated, so is CP.

But the most profound consequence of the CPT theorem shows up as a very deep connection between relativity and quantum physics: Lorentz invariance. If the CPT symmetry is a good symmetry, then the Lorentz symmetry — which states that the laws of physics stay the same for observers in all inertial (i.e., non-accelerating) reference frames — must also be a good symmetry. The reverse of this, however, is also true, implying that if you violate the CPT symmetry, then the Lorentz symmetry is also broken.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

For a number of reasons, this is not only bad, but has the potential to be pathological: destroying the foundation upon which modern physics is built.

Breaking Lorentz symmetry might be fashionable in certain areas of theoretical physics, particularly in certain quantum gravity approaches, but the experimental constraints on this are extraordinarily strong. There have been many experimental searches for violations of Lorentz invariance for over 100 years, and the results are overwhelmingly negative and robust. If the laws of physics are the same for all observers, then CPT must be a good symmetry. And if they aren’t, then the ways in which they are broken are tiny, unobserved, and extremely tightly constrained.

Quantum gravity tries to combine Einstein’s General theory of Relativity with quantum mechanics. Quantum corrections to classical gravity are visualized as loop diagrams, as the one shown here in white. If you extend the Standard Model to include gravity, the symmetry that describes CPT (the Lorentz symmetry) may become only an approximate symmetry, allowing for violations. Thus far, however, no such experimental violations have been observed.

In physics, we have to be willing to challenge our assumptions, and to probe all possibilities, no matter how unlikely they seem or how strongly they violate our intuitive sense of how nature ought to behave. But our default should be that the laws of physics that have stood up to every experimental test, that compose a self-consistent theoretical framework, and that accurately describe our reality, must be treated as though they are correct until proven otherwise. In this case, it means that the assumption that the laws of physics are the same everywhere and for all observers should be treated as valid until proven otherwise.

Sometimes, particles behave differently than antiparticles, and that’s okay. Sometimes, physical systems behave differently than their mirror-image reflections, and that’s also okay. And sometimes, physical systems behave differently depending on whether the clock runs forward or backward, which is also admissible. However, we have to demand that the same behaviors will be seen for

• particles moving forward in time
• as for antiparticles reflected in a mirror moving backward in time;

that’s a consequence of the CPT theorem. That’s the one symmetry, as long as the physical laws that we know of are correct, that must be truly unbreakable in our Universe.