Why modifying gravity doesn’t add up

- If you add up all the normal matter in the Universe and calculate the expected gravitational effects from General Relativity, what we predict doesn’t match what we see.
- While dark matter has long been the favored, consensus model due to its extraordinary explanative power, a competing idea is to modify the theory of gravity.
- Yet, when we look at the outcome of doing so in detail, we find that modifying gravity is severely lacking in what it can do compared to dark matter. Here’s why it doesn’t add up.
When we look out at the Universe — from the Moon, planets, and objects in our Solar System to the stars, galaxies, and even grander structures — we assume that all of these systems obey the same fundamental laws. We also assume that the full suite of what we observe can be explained by the same sets of particles that govern our own existence. Unfortunately, at least one of these two assumptions must be wrong, as applying the known laws of physics to the particles of the Standard Model known to exist cannot explain the full suite of structures and behaviors that we observe.
It’s long been realized that adding just one additional ingredient to the Universe can explain the behavior of all the structures that we see. That ingredient, known as dark matter, would have the following properties:
- it would always be cold, or moving slowly compared to the speed of light,
- it would exist in five times the abundance of normal matter,
- it would gravitate, but wouldn’t experience the electromagnetic or nuclear interactions,
- it wouldn’t collide with either itself or with any of the Standard Model particles,
- but it would curve space just as surely as any entity with mass or energy would.
Dark matter is the leading explanation for this puzzle for a variety of reasons. But it’s also possible, just like novel phenomena appear on subatomic scales, that there are novel gravitational phenomena that appear under certain cosmic conditions. This would require not a modification to the composition of the Universe, but a modification to our understanding of gravitation. It’s a compelling idea worthy of consideration, but one we must examine in detail to see if it truly adds up.

Observationally, we’ve known something was amiss with the simplest assumption about the Universe for a long time: assuming that General Relativity plus the physics of atoms governed all structures in the Universe. Sure, this works perfectly well in experiments here on Earth as well as for observations throughout the Solar System, but on galactic scales and larger, it falls apart.
In the 1930s, astronomer Fritz Zwicky was observing individual galaxies within the Coma Cluster: a dense, nearby cluster of more than 1000 galaxies in the relatively nearby Universe. When he calculated the mass of the cluster from the starlight he observed, he got a number; when he calculated how much mass needed to be in the cluster from the observed motions of the individual galaxies within it, he got a different number. The only problem? The numbers differed by a tremendous amount: a factor of ~160.
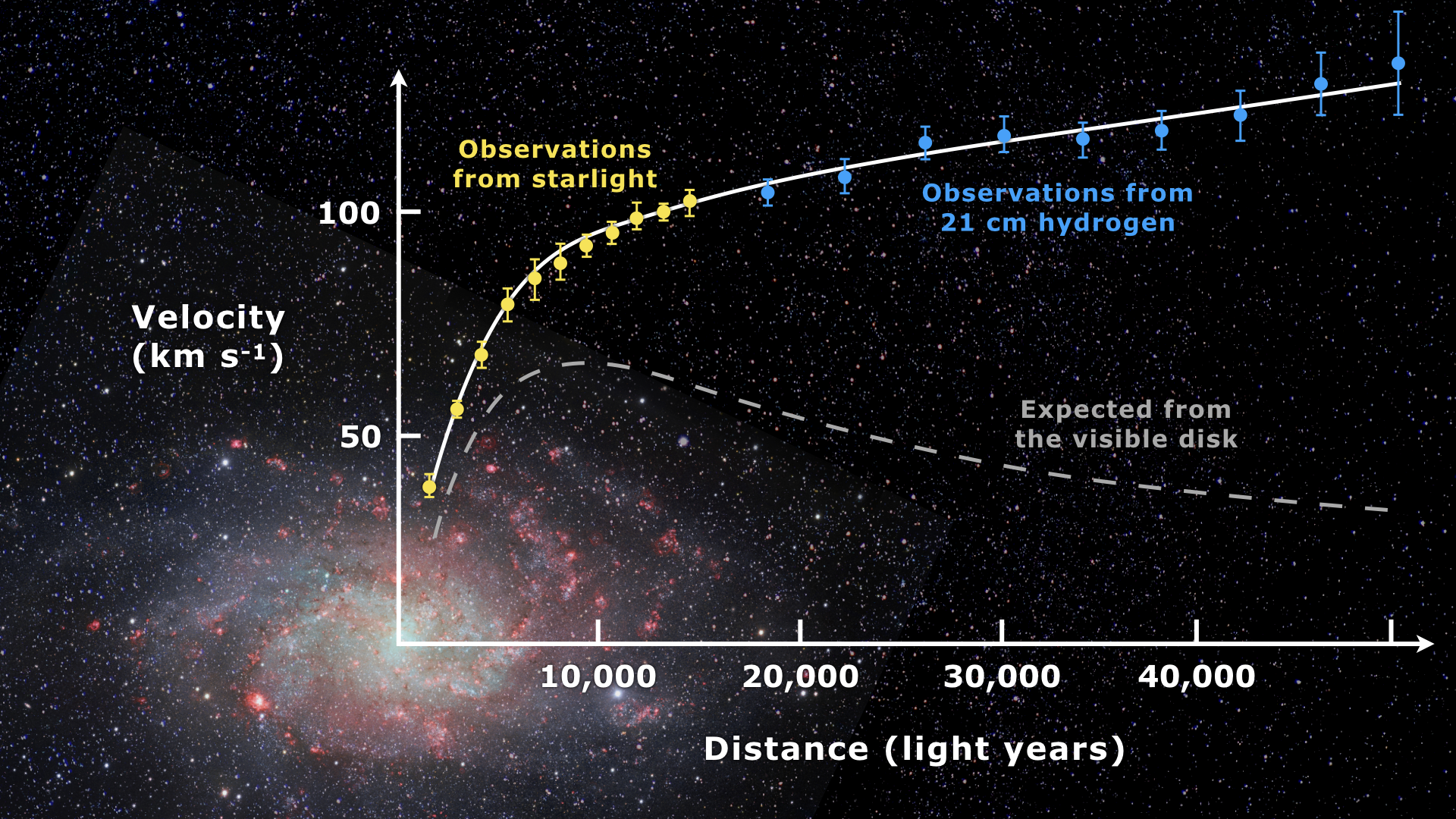
This problem was largely ignored until the 1970s, as most astronomers presumed there was simply an undiscovered source of matter within the galaxies and the cluster itself. But starting with the pioneering work of Vera Rubin, we started to see that same phenomenon within individual, rotating galaxies as well. As you moved farther away from the galactic center, the rotation speeds didn’t drop as you’d gravitationally expect, but remained high all the way to the edge of observability.
As time went onward, the improved observational evidence only appeared to strengthen these problems. Many problems with Zwicky’s factor of ~160 were found:
- he underestimated the mass-to-light ratios of a typical star by about a factor of 3,
- he underestimated the mass fraction in gases, as opposed to just stars,
- and he underestimated the mass fraction of clusters in the form of plasmas.
When you put these factors together, however, a discrepancy still remained: a mismatch of about a factor of six. Additionally, Rubin (and then others) observed many individual galaxies, finding the same problems for both gas-rich spirals and gas-poor ellipticals alike: their rotational speeds didn’t fall off at high distances from the galactic centers, but remained large. Sometimes they slightly increased or decreased, but they mostly remained large.
Taking these two sets of observations together, it’s clear that something was amiss. Perhaps there was some unseen form of mass present: the dark matter hypothesis. But perhaps another explanation should be considered: perhaps one only needed to modify the law of gravity. The first serious attempt came in the early 1980s, when physicist Moti Milgrom put forth a wild but compelling idea: MOND, for MOdified Newtonian Dynamics.

What MOND hypothesized was fascinating: that very far from the centers of galaxies, on scales of thousands of light-years or more, the predicted accelerations of stars around their galactic centers would be extremely small, but they’re being pulled by a system, overall, of tremendously substantial (normal matter) mass. If the acceleration caused by that central mass drops below a critical value — a new hypothesized constant of nature — then the acceleration isn’t determined by the gravitational force (or curvature of space) caused by the dominating mass, but rather reverts to that minimal value.
In other words, unlike in our Solar System, where the planets and other rocky, icy, and gaseous bodies all orbit the Sun with ever-decreasing speeds the farther away from the Sun they get, stars within larger cosmic structures obey a different rule. As you move farther away from the center of a galaxy, the speed at which stars move around it asymptotes toward some minimum value: a constant that’s proportional to (the fourth root of):
- the total amount of normal matter within that galaxy,
- the gravitational constant,
- and that new hypothesized constant of “minimal acceleration.”
Remarkably, this one modification to gravity successfully explains the motions of individual stars within all known types of galaxies, except the extremely rare, recently discovered populations of galaxies that appear to lack dark matter (or the effects typically seen from modified gravity) entirely.
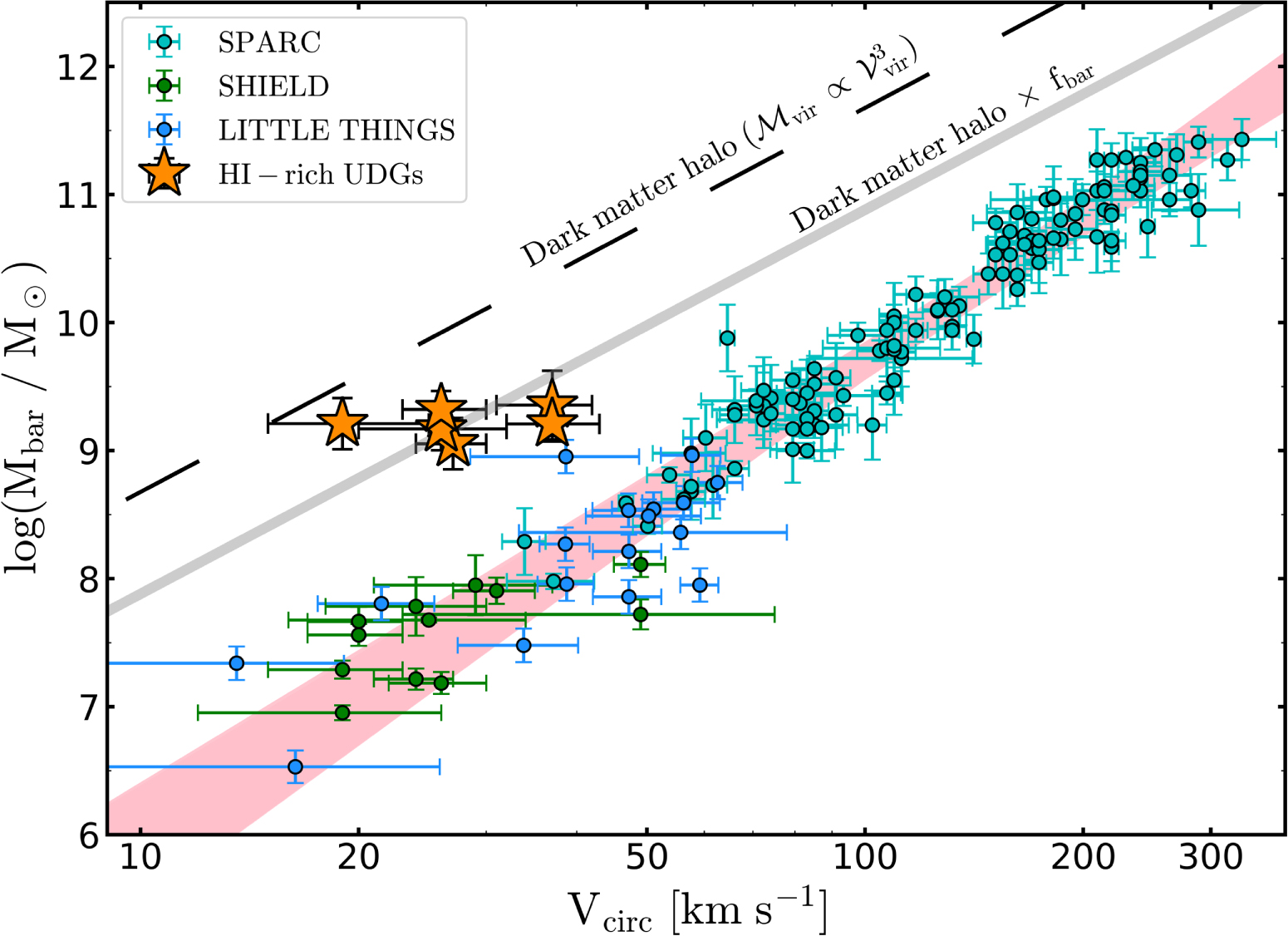
From tiny spiral galaxies to massive, giant ones, from dwarf spheroidal galaxies to enormous elliptical ones, this one simple rule — that there’s a minimal value for accelerations of astrophysical bodies at galactic scales and larger — works remarkably well for individual galaxies. Even when looking at the motions of small, satellite galaxies around large, massive ones, this same MONDian rule of a minimal acceleration appears to describe their motions extremely precisely. Moreover, in this particular regime, MOND can even outperform dark matter in gory detail, leading to much more consistent and accurate predictions for the motions of galactic components than dark matter simulations can.
Moreover, there are some interesting theoretical parallels that further support the idea of modified gravity as, perhaps, a step toward a more fully fundamental theory. In electromagnetism, the behavior of electric and magnetic fields changes if you’re in a dielectric medium, rather than in the vacuum of empty space; the modification to Newtonian gravity that gives you MOND behaves very analogously: like a gravitational dielectric. If you want to merge MOND with Einstein’s General Relativity, it is possible as well, simply by adding in scalar (and possibly vector) terms in addition to the standard metric tensor terms.
As long as you fulfill some basic consistency criteria:
- that you can recover standard General Relativity on Solar System scales,
- that your speed of gravity equals the speed of light and gravitational waves behave as standard General Relativity predicts,
- and that, on scales up to a couple of million light-years, the additional acceleration term takes over for otherwise smaller galaxy-scale accelerations,
these modifications to gravity seem like an extremely promising avenue. Indeed, a large number of researchers are often drawn in by this allure, and the plausibility of explaining the observed Universe without adding ingredients whose evidence only exists indirectly: through its gravitational effects.
But the Universe is a lot more than what happens on Solar System and galactic scales; there’s literally a whole cosmos out there. In fact, the earliest evidence for dark matter didn’t appear on these scales, but larger ones: on the scales of galaxy clusters. With the aforementioned prescription for modifying gravity, we should be able to tease out predictions for how individual galaxies move within galaxy clusters. Indeed, we get one, but here’s where the good news ends: the predictions fail to match observations, giving speeds that are too low — on scales extending from the cluster center out to several million light-years from it — by factors of 50-80%.
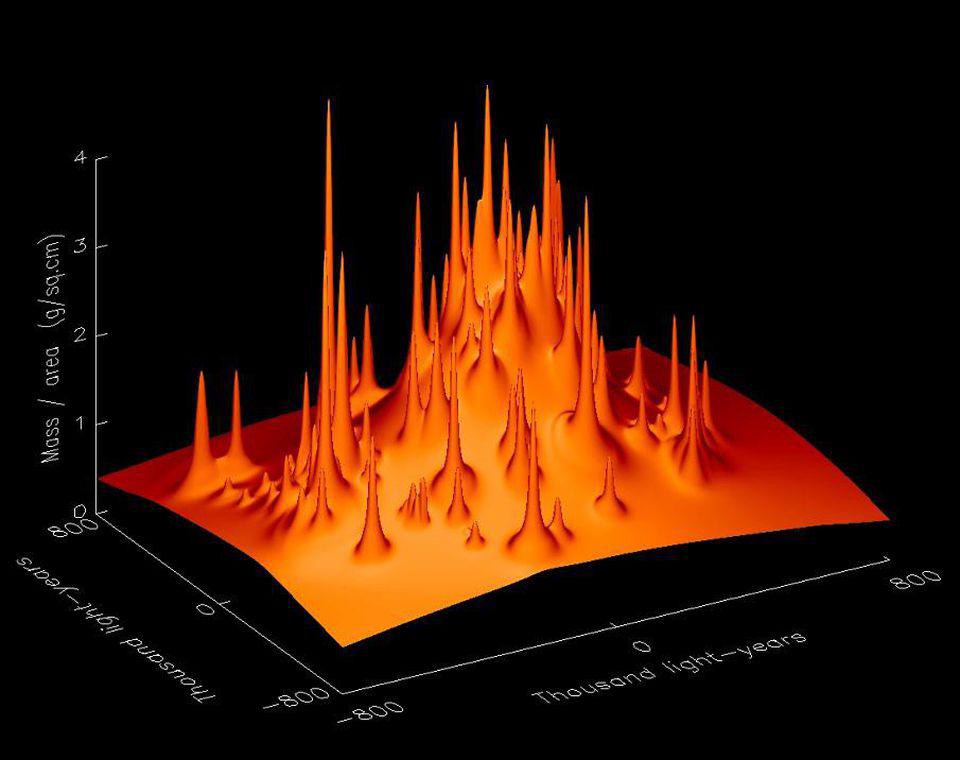
How can you reconcile this if you still want to save modified gravity without having to throw in dark matter? (Or, alternatively, a new type of field or interaction that behaves indistinguishably from dark matter?) There are only two ways.
- You can postulate an additional separate modification of gravity that comes into play on cluster scales.
- You can hypothesize that there is additional matter, hitherto unseen, over and above what’s known, expected, observed, and calculated to be present in galaxy clusters.
We have a saying in cosmology that strongly applies to the first line of thought, “You only get to invoke the Tooth Fairy once.” In other words, you’d have to modify gravity in two separate ways to account for the two separate problems you find on multiple distance scales. If you’re now worried about extrapolating to even larger cosmic scales and whether you’d need a third modification if you went down this route, I’ll say this: you’re not only right to worry, but you’d need a fourth such modification if you wanted to account for dark energy as well.
But the second avenue — the hypothesizing of additional normal matter in galaxy clusters — comes along with other problems that are perhaps even more alarming.

Some galaxy clusters exhibit gravitational lensing signals, magnifying and distorting the light from background objects behind them. This again requires additional matter, particularly toward cluster centers: where modified gravity predicts large accelerations.
Some galaxy clusters are hot, where the gases inside emit X-rays. This places severe constraints on how much “additional normal matter” there can be, in conflict with the above observations.
Some galaxy clusters are in some stages of a cluster collision: with clusters approaching one another, striking each other, slowing down to merge after their initial interaction, or settling down in the aftermath of such an interaction. As you might expect, the majority of the normal matter from within the cluster “splats” together in between the two clusters, revealing X-rays. However, the gravitational effects appear in regions as though the two clusters simply passed through one another: not in the location where the majority of the normal matter is located.
Either gravity is suddenly a non-local force — having effects based on where the matter is not — or the presence of dark matter is unequivocally revealed by precisely this class of system.

Importantly, we find that there are also galaxy clusters headed toward one another in a pre-collisional state, and in those instances, there is no separation of normal matter from the gravitational effects. If dark matter is present, that phenomenon is easy to explain: the normal matter and dark matter are separated by the collision, as normal matter interacts, heats up, slows down, and emits X-rays, while dark matter simply “coasts,” influenced only by gravity. But if there’s a modification to gravity, it’s very difficult to explain why post-collisional clusters exhibit non-local gravitational effects, but not pre-collisional clusters. On top of all of this, there is no room for “additional normal matter” in the Universe, as the total amount of cosmic normal matter is definitively known and tightly constrained by Big Bang Nucleosynthesis: a theoretical and observational set of information entirely divorced from the dark matter/modified gravity question.
But at last, we come to cosmic scales in the most important ways: the large-scale structure of the Universe and the leftover glow from the Big Bang, the Cosmic Microwave Background (CMB). These are absolute killers for modified gravity, as every probe of them requires an additional ingredient (or a modification of gravity equivalent to adding such an ingredient) that’s equivalent to dark matter’s effects. The cosmic web requires it; galaxy-galaxy correlations require it; the power spectrum of the Universe requires it; and in particular the seven observed acoustic peaks in the CMB absolutely require it. Without dark matter or an equivalent mimic, the third, fifth, and seventh acoustic peaks wouldn’t exist!
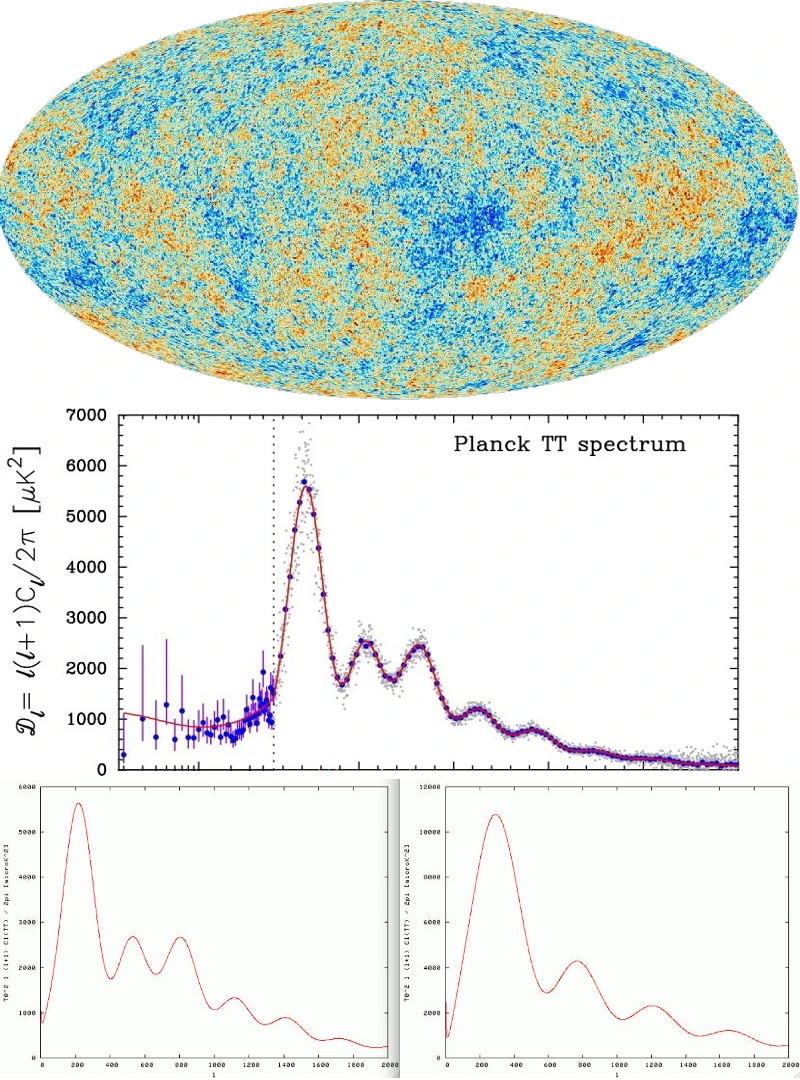
This is the major set of problems with considering modified gravity as a serious alternative to dark matter. The modifications of gravity that work on galactic scales — and yes, admittedly, that work very well on galactic scales — don’t adequately work on larger cosmic scales. If you want your theory of modified gravity to work on those scales, you either need to adopt a dark matter mimic to explain them, or you need to invoke additional modifications atop the initially well-motivated one. In either case, you lose the simplicity of the “one new addition, many problems solved” approach that makes dark matter so attractive.
Part of the way that we advance our understanding of the Universe is by challenging our most cherished and accepted theories as valiantly as possible: by attempting to knock them down from all angles, and by seeking alternatives that can do the job just as well or even better than they can. On galactic scales, modified gravity can absolutely do that, and dark matter models have to face the challenges before them: of working through the nonlinear structure formation, the feedback from star formation, the dynamical heating of dark matter in galactic and cluster cores, etc., to better match observations. But on cluster scales, cosmic scales, and from early times to late ones, dark matter is exquisitely successful in realms where modified gravity requires a mix of special pleading and an unhealthy amount of self-delusion.




