Ask Ethan: How can matter be mostly empty space?

One thing you can be sure of, as you measure and observe the Universe around you, is this: the physical objects you see, touch, and otherwise interact with all occupy a volume of space. Whether in the form of solid, liquid, gas, or any other phase of matter, it costs energy in order to reduce the volume that any tangible material occupies, as though the very components of matter themselves are capable of resisting the impetus to occupy a smaller amount of three-dimensional space.

And yet, seemingly paradoxically, the fundamental constituents of matter — the particles of the Standard Model — occupy no measurable volume at all; they’re simply point particles. So how, then, can substances made out of volume-less entities come to occupy space at all, creating the world and Universe as we observe it? That’s what Pete Sand is curious about, asking:

“How can this chair be a chair and also a quantum probability and also mostly empty space?  

How do those different realities co-exist?

How can the same “object” follow one set of physics at a conventional scale and another set of physics at the quantum scale?”

Let’s start by breaking down the matter we’re familiar with, step-by-step, until we go all the way down to the quantum rules that underpin our existence. Finally, we can work our way up from there.

The size, wavelength, and temperature/energy scales that correspond to various parts of the electromagnetic spectrum. You have to go to higher energies, and shorter wavelengths, to probe the smallest scales. Ultraviolet light is sufficient to ionize atoms, but as the Universe expands, light gets systematically shifted to lower temperatures and longer wavelengths.

If you want to understand volume, you have to understand the way we make the measurements that reveal how large an object is. The way you determine the size of a macroscopic entity is typically to compare it to some standard of reference whose size is known: a ruler or other measuring stick, the amount of force that a spring (or spring-like object) is displaced by owing to that object, the light-travel-time it takes to cross the span of an object, or even through experiments that strike an object with a particle or photon of a particular wavelength. Just as light has a quantum mechanical wavelength defined by its energy, particles of matter have an equivalent wavelength — their de Broglie wavelength — regardless of their other properties, including their fundamental/composite nature.

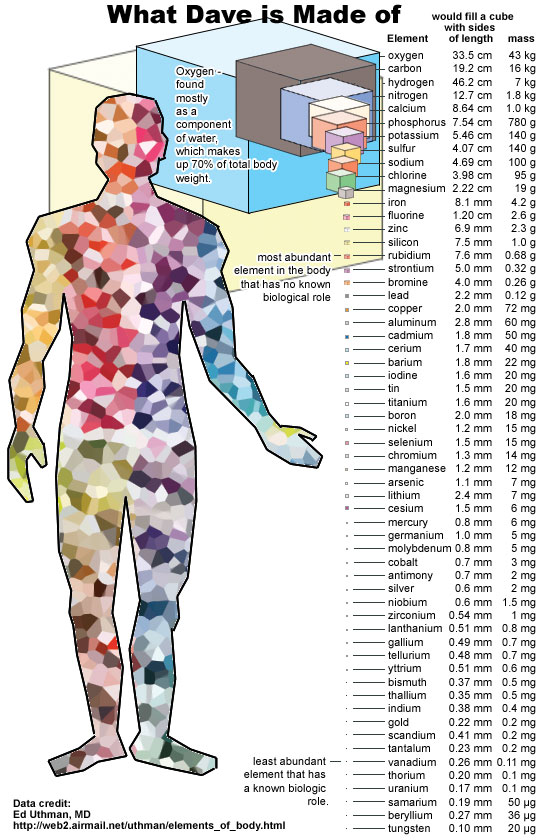
When we break down matter itself, we find that everything we’re familiar with is actually made of smaller constituents. A human being, for example, can be broken down into their individual organs, which in turn are made of individual units known as cells. A fully grown human adult might have between 80-100 trillion cells in them all told, where only about 4 trillion of them make up what you typically think of as your body: your musculoskeletal system, connective tissue, circulatory system, and all of your vital organs. Another 40 trillion or so are blood cells, while fully half of the cells in your body do not have your genetic material at all. Instead, they’re made of single-celled organisms such as bacteria that live largely in your intestines; from a certain point of view, half of your cells are not even you!

Although human beings are made of cells, at a more fundamental level, we’re made of atoms. All told, there are close to ~10^28 atoms in a human body, mostly hydrogen by number but mostly oxygen and carbon by mass.

Cells themselves are relatively small, typically spanning only ~100 microns across or so and usually requiring a microscope to resolve individually. However, cells aren’t fundamental at all, but can be further broken down into smaller constituents. More complex cells contain organelles: cell components that perform specific biological functions. Each of those components, in turn, is composed of molecules, which range in size from nanometers on up; a single DNA molecule, although very thin, can be longer than a human finger when stretched straight!

Molecules, in turn, are made up of atoms, where atoms are roughly just one Ångstrom across, and typically exhibit spherical symmetry, having the same extent in all three dimensions. For a long time in the 19th century, it was assumed that atoms were fundamental; their very name, atom, means “unable to be cut.” But later experiments showed that atoms themselves were made of still smaller constituents: electrons and atomic nuclei. Even today, electrons cannot be broken apart into smaller constituents, but atomic nuclei have a finite size after all: they’re typically a few femtometers across, existing on distance scales ~100,000 times smaller than an atom itself.

Although, by volume, an atom is mostly empty space, dominated by the electron cloud, the dense atomic nucleus, responsible for only 1 part in 10^15 of an atom’s volume, contains ~99.95% of an atom’s mass. Reactions between internal components of a nucleus can be more precise and occur on shorter timescales, as well as at different energies, than transitions restricted to an atom’s electrons.

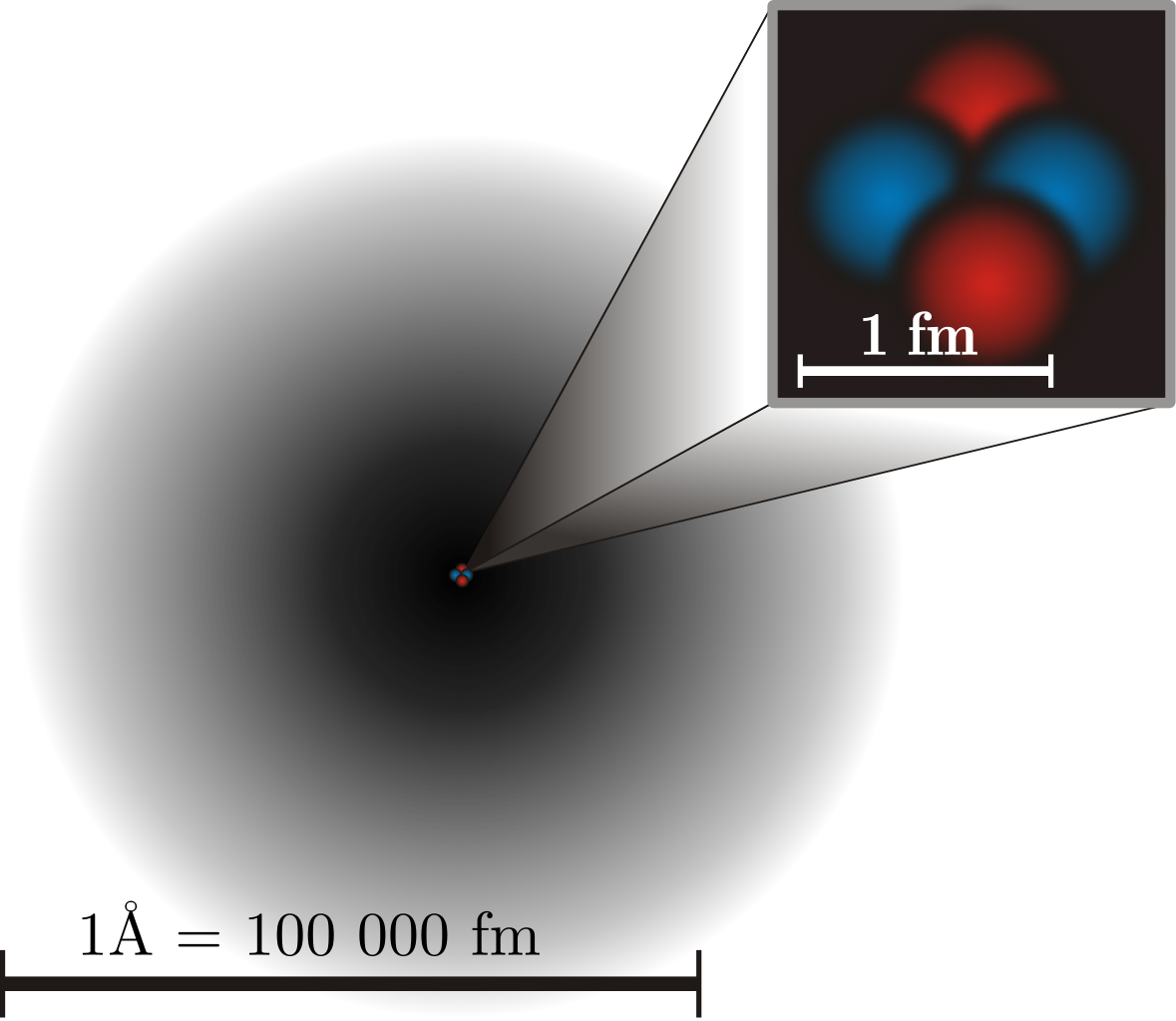
But even atomic nuclei aren’t elementary particles; they’re composed of still smaller entities. Each atom’s nucleus is made of either a single proton or a mix of protons and neutrons, where an individual proton (or neutron) has been measured to be between 0.84 and 0.88 femtometers in diameter.  Protons and neutrons themselves can be further broken down into components: quarks and gluons. At last — at least according to current best experimental and observational results — we’ve come to the fundamental entities that make up most of the normal matter we interact with in our daily lives: electrons, gluons, and quarks.

High-energy physics experiments involving particle colliders have placed the tightest constraints on how large-or-small these elementary particles can be. Owing to the Large Hadron Collider at CERN, we can definitively state that if any of these particles do have a finite size, and/or are made up of still-smaller constituents, our most powerful accelerator-and-collider has been unable to crack them open. Their physical sizes must be smaller than ~100 zeptometers, or 10^-19 meters.

Somehow, the fundamental constituents that make up everything we interact with have no measurable size at all, behaving as truly dimensionless point particles, and yet they bind together to produce the full suite of entities we find at all scales: protons and neutrons, atomic nuclei, atoms, molecules, cell components, cells, organs, and living beings among them.

The journey from macroscopic scales down to subatomic ones spans many orders of magnitude, but going down in small steps can make each new one more accessible from the previous one. Humans are made of organs, cells, organelles, molecules, atoms, then electrons and nuclei, then protons and neutrons, and then quarks and gluons inside of them. This is the limit to how far we’ve ever probed nature.

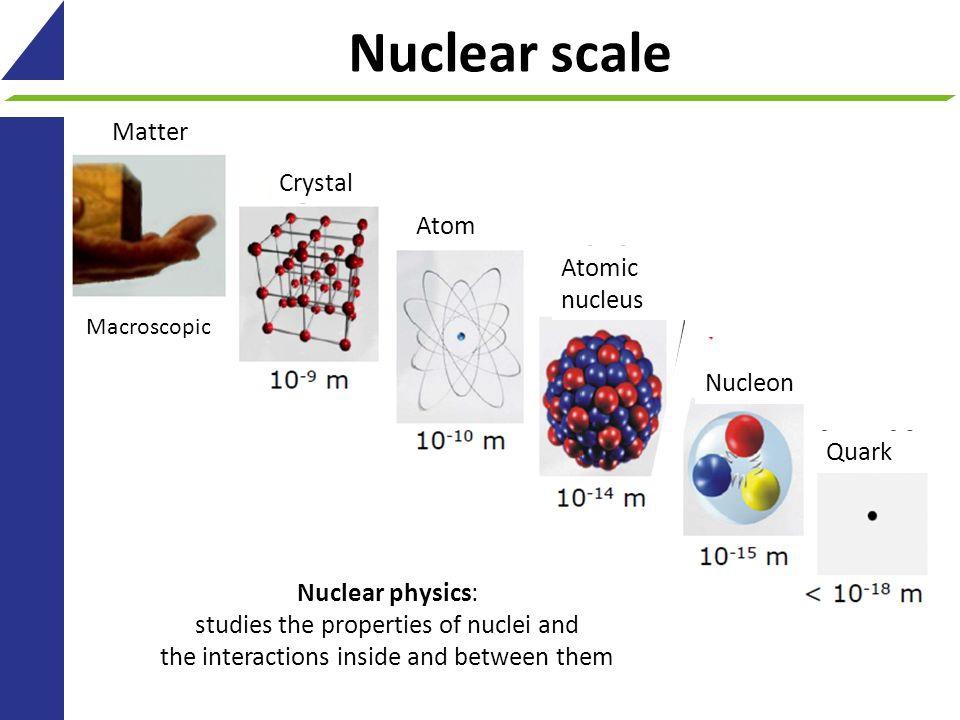
So how does that work? How can point-like particles — particles of possibly an infinitesimal size — combine together to make physical objects that have a positive, finite, non-zero size?

There are three aspects to this, and all three of them are required to understand the Universe around us. 

The first is the fact that there’s a quantum rule — the Pauli Exclusion Principle — that prevents any two identical quantum particles of a certain type from occupying the same quantum state. Particles come in two varieties, fermions and bosons, and while there are no restrictions on how many identical bosons can occupy the same quantum state in the same physical location, the Pauli Exclusion Principle applies to all fermions. Given that each type of quark and every electron is a fermion, this rule excludes even infinitesimally small particles from coexisting in the same volume of space. Just based on this rule alone, you can see how multiple particles, even if they don’t have a “size” themselves, are required to be separated from one another by a finite distance.

This diagram displays the structure of the standard model (in a way that displays the key relationships and patterns more completely, and less misleadingly, than in the more familiar image based on a 4×4 square of particles). In particular, this diagram depicts all of the particles in the Standard Model (including their letter names, masses, spins, handedness, charges, and interactions with the gauge bosons: i.e., with the strong and electroweak forces). It also depicts the role of the Higgs boson, and the structure of electroweak symmetry breaking, indicating how the Higgs vacuum expectation value breaks electroweak symmetry and how the properties of the remaining particles change as a consequence. Neutrino masses remain unexplained.

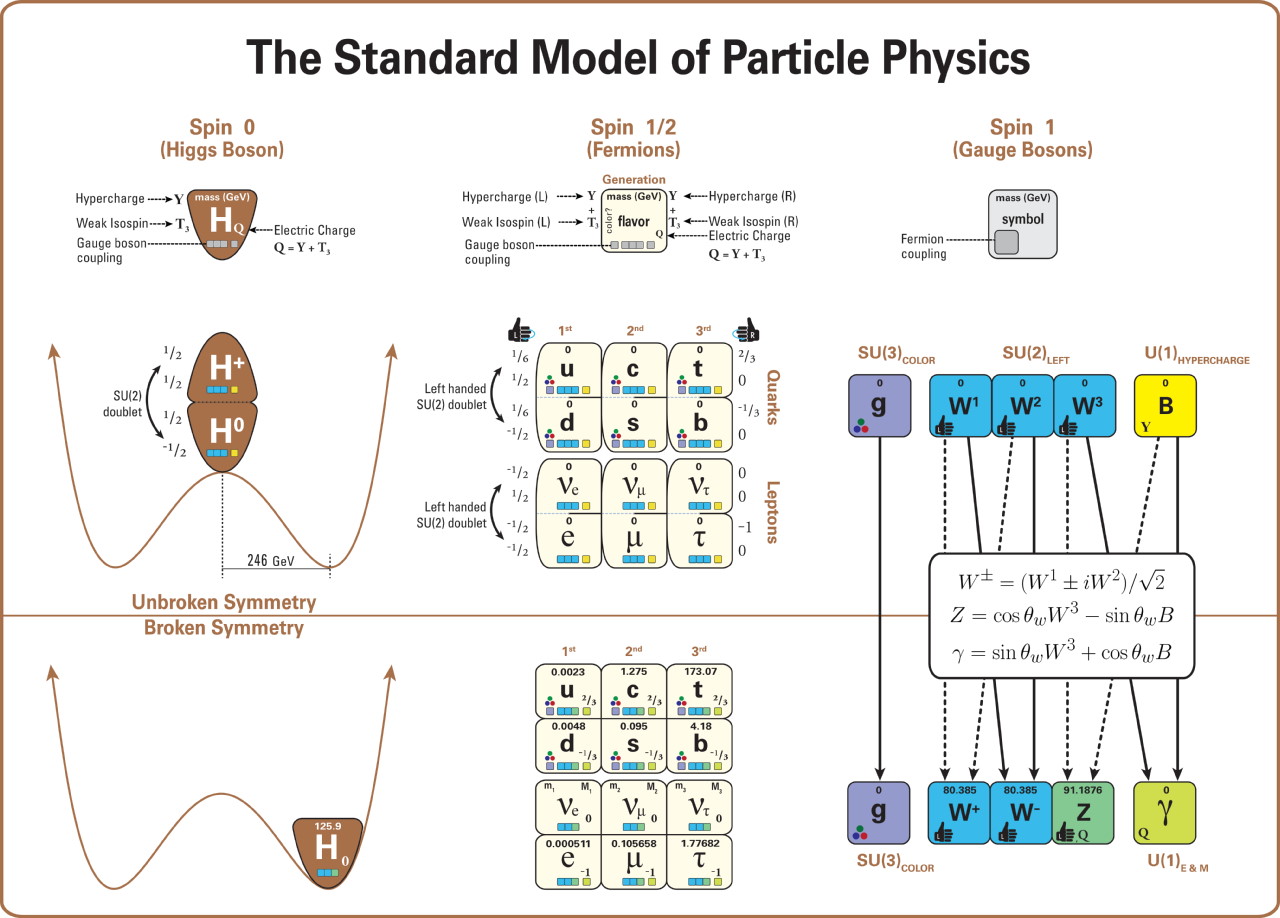
The second aspect is that these particles have fundamental properties inherent to them, and those properties include things like electric charge, weak isospin and weak hypercharge, and color charge. Fermionic particles — the ones subject to the Pauli Exclusion Principle — that possess an electric charge will experience the electromagnetic force, coupling to the photon. Fermionic particles with weak isospin and weak hypercharge experience the weak nuclear force, coupling to the W and Z bosons. And Fermionic particles with a color charge experience the strong nuclear force, coupling to the gluons.

As it turns out, quarks and electrons (along with the electron’s two heavier, fundamental cousins, the muon and tau particles) all have electric charges to them, meaning they all experience the electromagnetic interaction. In electromagnetism, like charges (either + + or – -) repel, while opposite charges (either + – or – +) attract, with the force getting stronger the closer the objects get. All of the quarks possess a color charge, meaning they all experience the strong nuclear force. The strong nuclear force is always attractive, but behaves in a less intuitive fashion: at very small particle separations, the strong force goes to zero, but increases the farther away two color-charged objects are from one another. If two composite objects are color-neutral overall but made up of entities that possess a color charge — like the proton and neutron — they exhibit what’s called a residual strong force: a force that attracts nearby objects with color-charged components, but that drops to zero very quickly as the distance between them rises.

The Pauli exclusion principle prevents two fermions from coexisting in the same quantum system with the same quantum state. It only applies to fermions, however, like quarks and leptons. It does not apply to bosons, and hence there is no limit to, say, the number of identical photons that can coexist in the same quantum state. It’s why fermion-containing stellar remnants, like white dwarfs and neutron stars, can hold themselves up against gravitational collapse, as the Pauli Exclusion Principle limits the volume that a finite number of fermions can occupy.

Meanwhile, all of the fundamental fermions have some type of weak charge (isospin and/or hypercharge), but that force can safely be ignored when considering the size of an object.

Finally, the third aspect that governs the sizes of objects in the Universe is a different fundamental, quantum property inherent to all fermions (and some bosons) in the Universe: mass. If an object is massless — that is, its mass is zero — it cannot remain still, but rather must always remain not only in motion, but in motion at the fastest speed allowable in the Universe: the speed of light. Photons are massless, gluons are massless, and gravitational waves are massless. They can all carry energy, but have no mass inherent to them, and as a result, they always move at the maximum speed allowable: the speed of light.

Thankfully, there are many entities in the Universe that do have mass, including all of the quarks, the electrons, and the (heavier) cousins of the electron: the muon and tau particles. Electrons are extremely light particles, while quarks range from “somewhat heavier” than the electron in the case of the up-and-down quarks to “the heaviest known fundamental particle of all” in the case of the top quark. Having a mass mandates that particles move slower than the speed of light, and even enables them to come to rest under the right conditions. If it weren’t for the massive nature of the quarks and electrons — and for the Higgs field that gives these particles their masses — forming bound states out of these objects like protons, atomic nuclei, atoms, and everything that’s subsequently built out of them would be entirely impossible!

The strong force, operating as it does because of the existence of ‘color charge’ and the exchange of gluons, is responsible for the force that holds atomic nuclei together. This force, governed by the exchange of massive gluons, is bounded by the speed of light; from inside a black hole’s event horizon, there’s no way that a force such as this can prevent any outermore particle from reaching the central singularity.

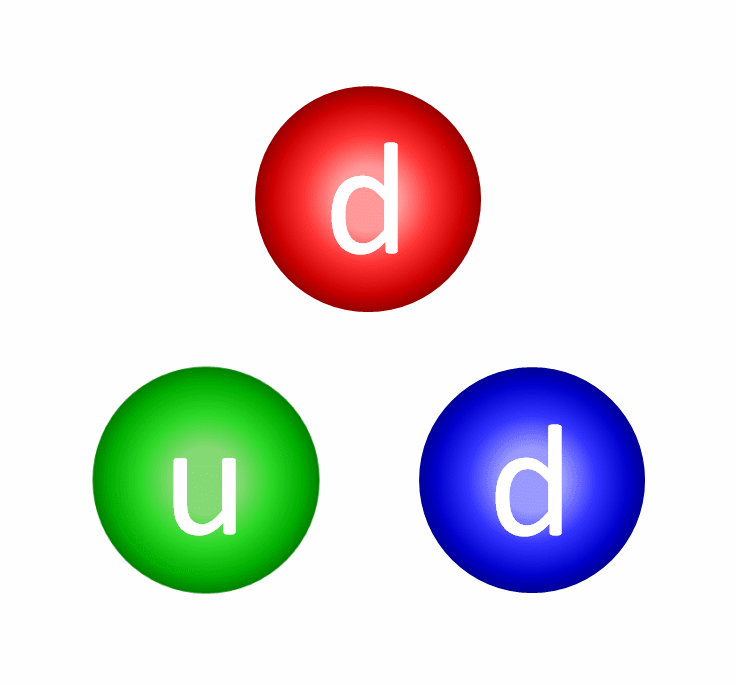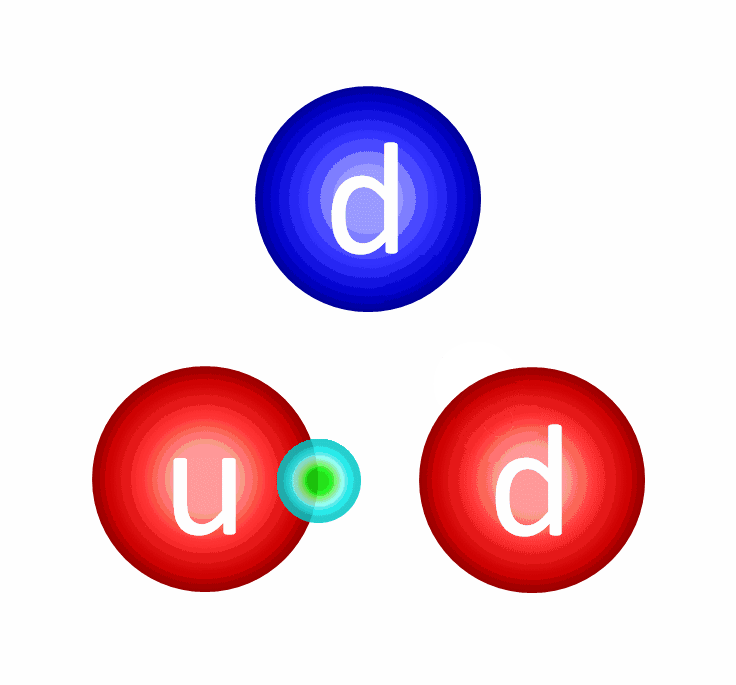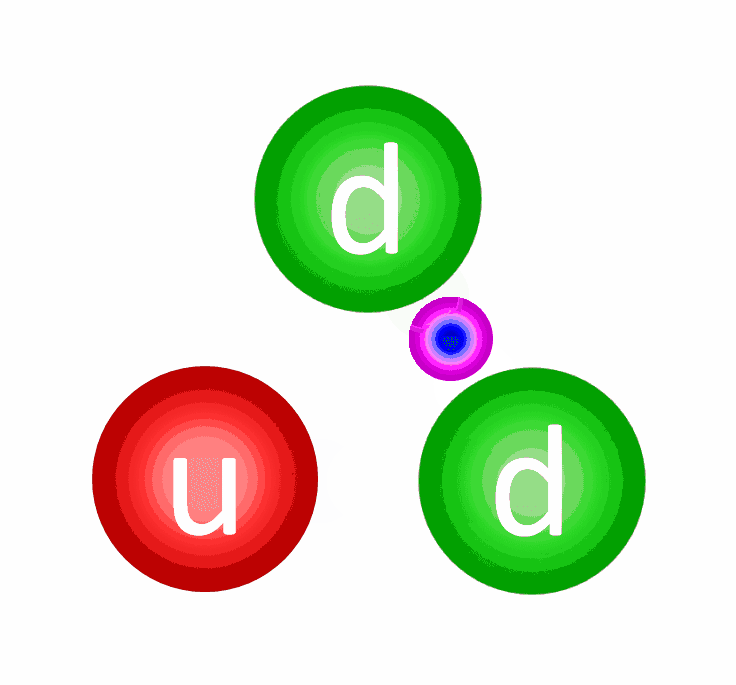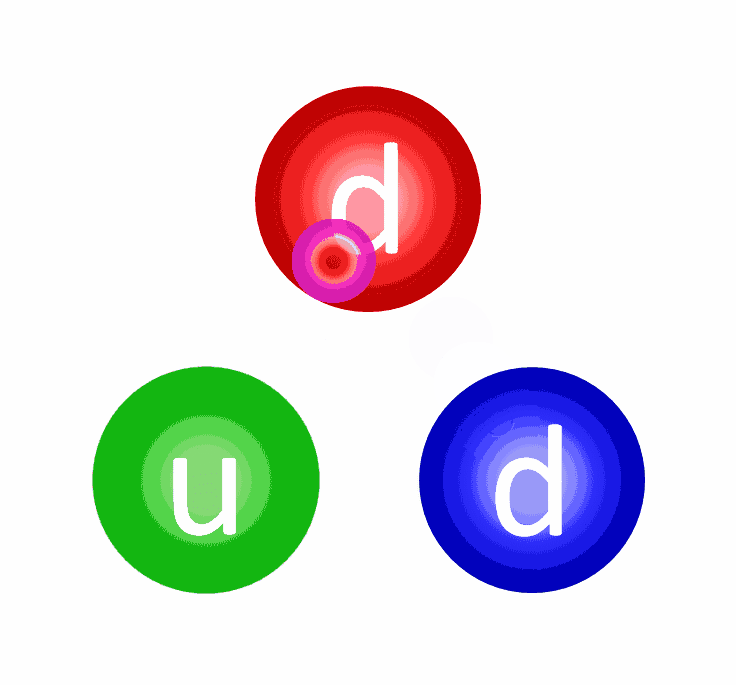
With those three aspects firmly in mind:

• no two identical fermions can occupy the same quantum state in the same location,
• particles have charges and those charges dictate the type and magnitude of force(s) that they experience,
• and some particles have a finite, positive, non-zero rest mass,

we can finally begin building objects of specific, finite sizes out of even infinitesimally-sized constituents.

Let’s start with protons and neutrons: entities made out of quarks and gluons. The quarks inside each proton and neutron have both electric and color charges. The electric force between similar quarks (up-up or down-down) causes repulsion, while the electric force between differing quarks (up-down or down-up) is attractive. When quarks get very close together, the strong force is negligible, meaning that if they were moving toward one another, they’ll simply “coast” past one another. However, the farther apart they get, the greater the attractive force between them gets, preventing them from getting too far apart. In fact, once the quarks inside a proton or neutron reach a critical separation distance from one another, the strong force causes them to “snap back” toward one another, just like a stretched spring would.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Because the quarks within a proton and/or neutron have non-zero masses, those quarks must always move slower than the speed of light, enabling them to accelerate, decelerate, and even (temporarily) come to rest within this composite structure. Combined, the strong and electromagnetic forces between quarks create protons and neutrons of finite sizes — a little under 1 femtometer apiece — while the binding energy between the quarks, due to the strong force, winds up being responsible for the majority of a proton’s and/or neutron’s total mass. Only ~1% of a proton’s/neutron’s mass arises from the quarks inside it, while the other ~99% comes from this binding energy.

Individual protons and neutrons may be colorless entities, but the quarks within them are colored. Gluons can not only be exchanged between the individual gluons within a proton or neutron, but in combinations between protons and neutrons, leading to nuclear binding. However, every single exchange must obey the full suite of quantum rules.

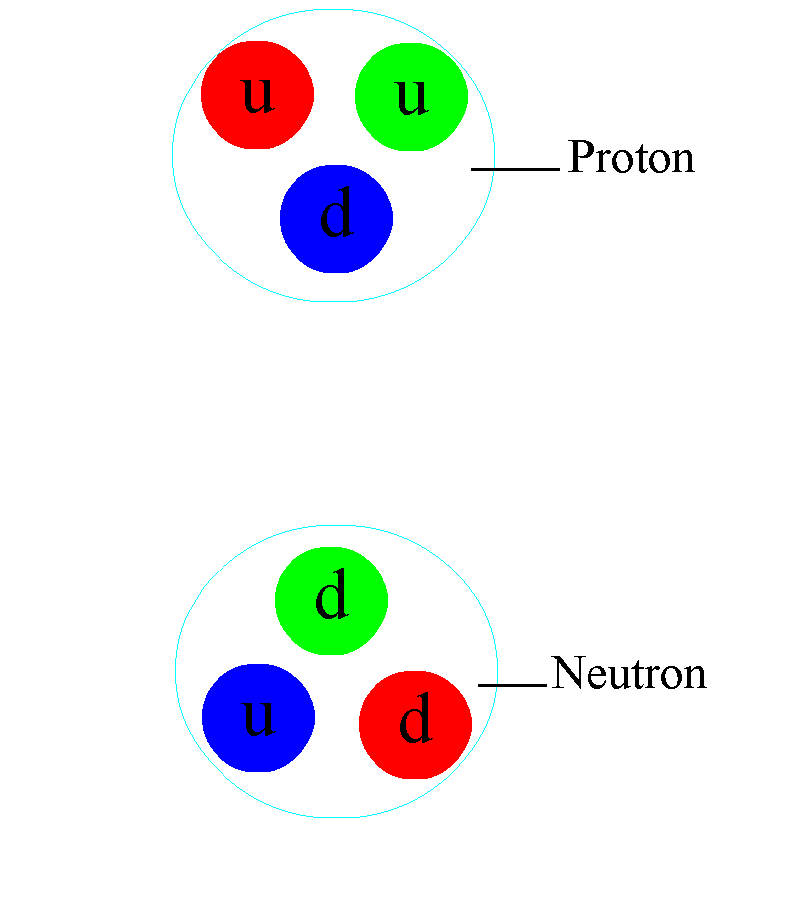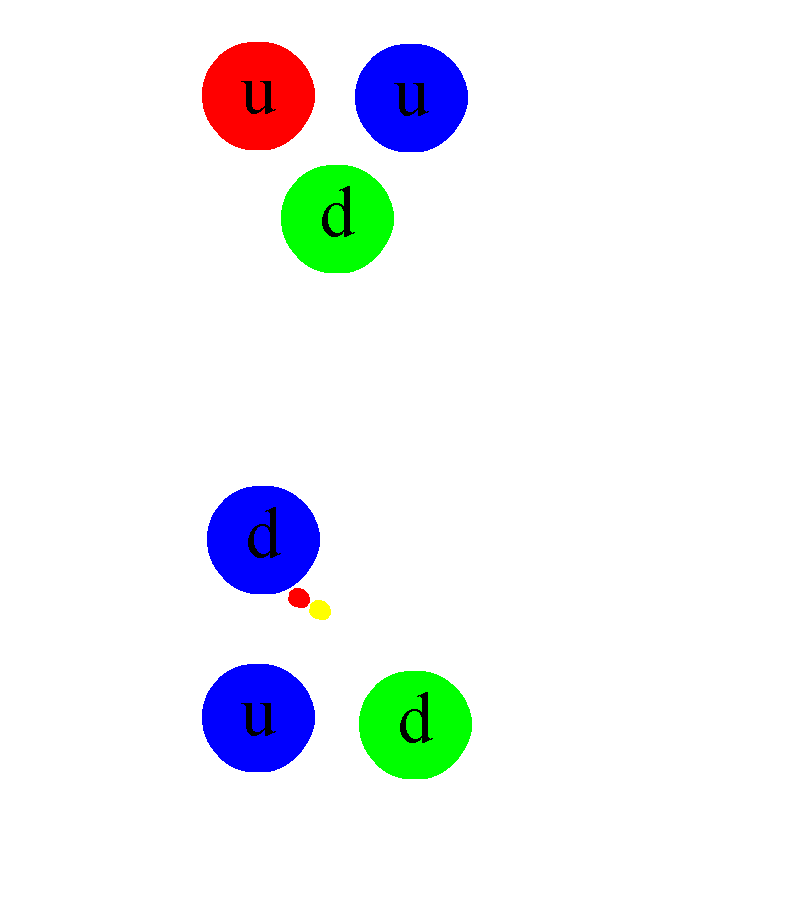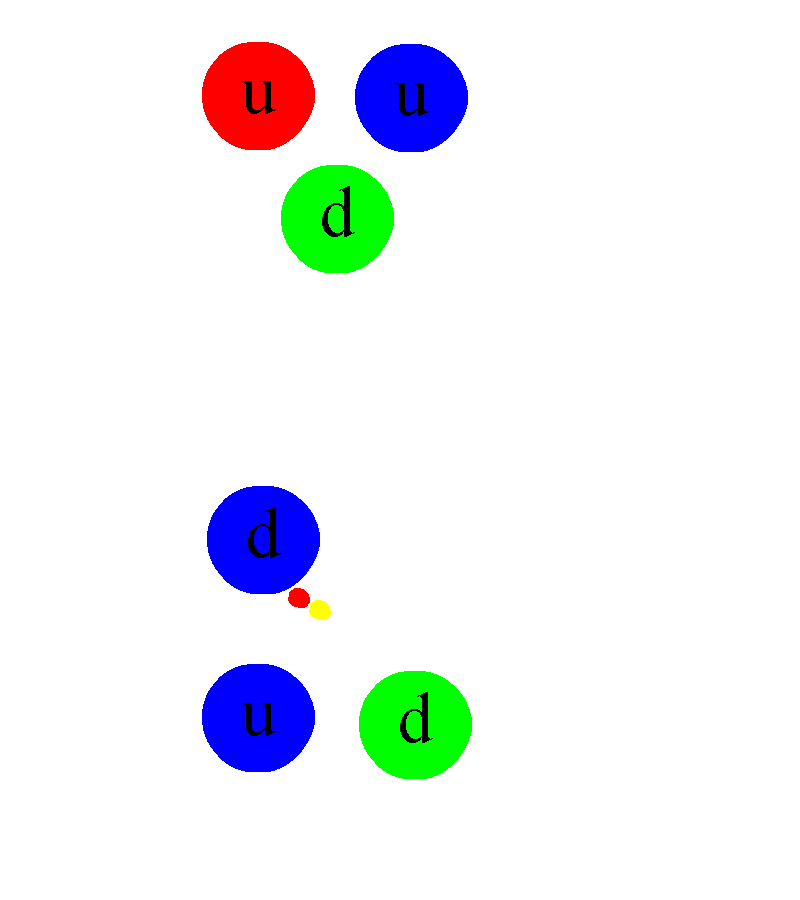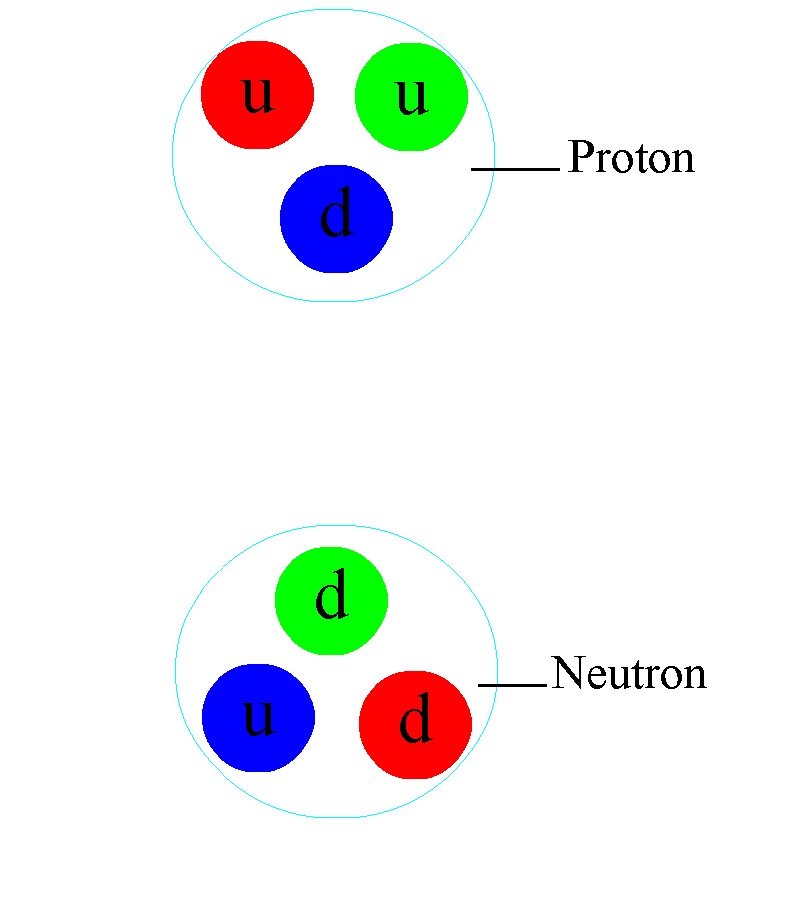
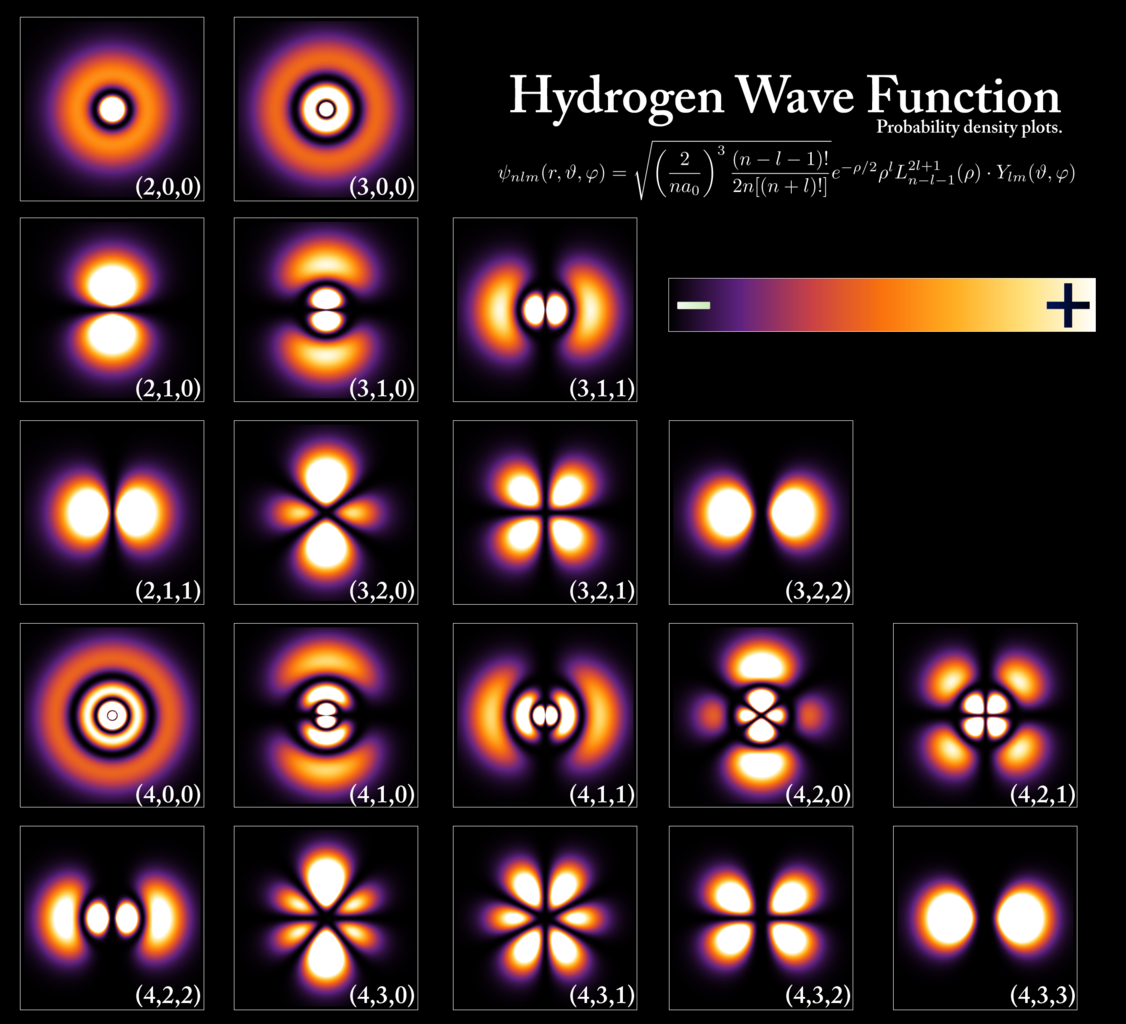
Atomic nuclei are a little simpler: the volume of an atom’s nucleus is approximately equal to the volume of its constituent protons and neutrons combined together. But for atoms themselves — atomic nuclei orbited by electrons — things get a little trickier. The electromagnetic force is now the one responsible for the size of an atom, as the positively charged, massive nucleus anchors the atom, and the negatively charged, much less-massive electron(s) orbit the nucleus. Because they have opposite charges to one another, atomic nuclei and electrons always mutually attract, but because each individual proton is 1836 times as massive as each individual electron, the electrons move rapidly around each atom’s nucleus. To no one’s surprise, the simplest atom is hydrogen, where only one electron orbits around a solitary proton, held together by the electromagnetic force.

Now, remember the Pauli Exclusion Principle: no two identical fermions can occupy the same quantum state in the same location. The hydrogen atom is small because its electron is in the lowest-energy state allowable, the ground state, and only has one electron. Heavier atomic nuclei, however — like carbon, oxygen, phosphorus, or iron — have more protons in their nuclei, requiring greater numbers of electrons within them. If the lower-energy quantum states are all full of electrons, then subsequent electrons must occupy higher-energy states, leading to larger electron orbits (on average) and “puffier” atoms that occupy greater volumes. Carbon atoms each have six electrons, oxygen atoms have eight, phosphorus atoms have fifteen, and iron atoms have twenty-six electrons apiece.

The more protons you have at the core of your atom, the more electrons you have orbiting within the outskirts of your atom. The more electrons you have, the greater the number of energy states that must be occupied. And the higher the energy state of the highest-energy electrons within your atom, the greater the amount of physical volume your atom must occupy. A hydrogen atom might be only about ~1 Ångstrom in diameter, but heavier atoms can be substantially larger: up to multiple Ångstroms across.

The energy levels and electron wavefunctions that correspond to different states within a hydrogen atom, although the configurations are extremely similar for all atoms. The energy levels are quantized in multiples of Planck’s constant, but the sizes of the orbitals and atoms are determined by the ground-state energy and the electron’s mass. Only two electrons, one spin up and one spin down, can occupy each of these energy levels owing to the Pauli exclusion principle, while other electrons must occupy higher, more voluminous orbitals. When you drop from a higher energy level to a lower one, you must change the type of orbital you’re in if you’re only going to emit one photon, otherwise you’ll violate certain conservation laws that cannot be broken.

Although atoms frequently assemble to form larger structures, the volume occupied by most objects can be mostly accounted for by understanding the volume occupied by an object’s constituent atoms themselves. The reason is simple: the Pauli Exclusion Principle, stating that no two identical fermions can occupy the same quantum state, prevents the electrons from adjacent atoms from infringing on the volume that the other one occupies. Using a human being as an example, we’re made mostly of carbon, oxygen, hydrogen and nitrogen, with phosphorus, calcium, iron, and other modestly heavy elements comprising the majority of the rest. Given that there are approximately ~10²⁸ atoms in a typical adult human body, if you assume that a typical atom is about ~2 Ångstroms on a side, that translates into a volume of around 80 liters for an adult human: about the size of a ~180 pound (80 kg) adult.

Under exceptional circumstances, of course, these rules can vary slightly. In a white dwarf star, for example, there are so many atoms packed together in one location that the electrons in orbit around their atomic nuclei actually get crushed by the compressive gravitational forces surrounding them, compelling them to occupy substantially smaller volumes than normal. In muonic atoms — where an atom’s electrons are replaced by the electron’s heavier cousin, the muon — atoms are only about 1/200th the diameter of electron-based atoms, as muons are approximately 200 times more massive than electrons. But for the conventional matter that make up our familiar experiences, it’s the cumulative effects of:

• the low but non-zero mass of the electron,
• the strong, negative electric charge of the electron,
• and the massive, positively charged atomic nucleus,
• combined with the Pauli Exclusion Principle, 

that give atoms, and hence all objects here on Earth, the volumes they occupy. From fundamental quantum entities all the way up to the macroscopic world we inhabit, that’s how fundamentally tiny, perhaps even point-like objects wind up occupying so much space!

Send in your Ask Ethan questions to startswithabang at gmail dot com!