Laser energy will never exceed this ultimate limit

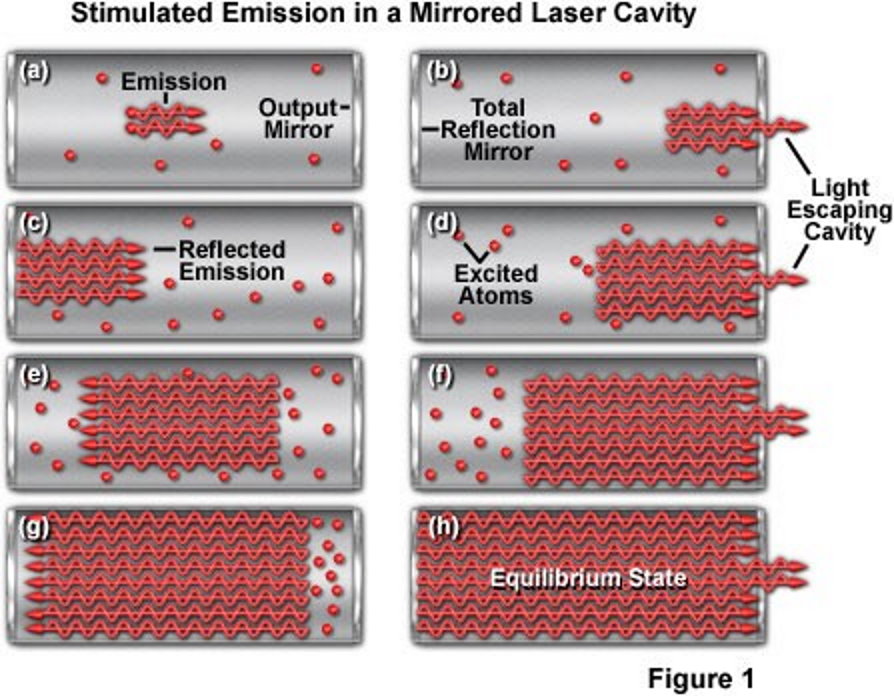
- Lasers work by stimulating the emission of radiation within a cavity, over and over, building up as many photons as desired before emitting them.
- It makes one wonder if you could use this technique to build up and produce a virtually limitless amount of energy, potentially all-at-once if desired.
- But it turns out this is not the case at all. There’s a fundamental limit to the amount of energy in lasers, set by an unlikely culprit: the rules of particle physics.
Back in the middle of the 20th century, there was really no good way to create purely monochromatic light: where all of the photons possessed precisely the same wavelength. Sure, you could break up white light into its component colors, such as by passing it through a prism or color filter, and selecting for only a narrow range of wavelengths, but that wouldn’t be truly monochromatic. However, the fact that atoms, molecules, lattices, and other structures only admit a specific set of electron transitions brought forth a fascinating possibility: if you could stimulate the same transition over and over, you could make truly monochromatic light.
Since 1958, we’ve managed to do precisely that with the invention of the laser. Over time, lasers have become more powerful, more widespread, and come in an enormous variety of wavelengths. By having photons of a specific wavelength build up in the lasing cavity, that same-frequency emission gets stimulated over and over again. But you cannot simply build up photons forever to get an arbitrarily large energy density in your laser; once you cross a certain threshold, the laws of physics themselves will stop you. Here’s why there’s an ultimate limit to laser energy, and we’ll never be able to exceed it.
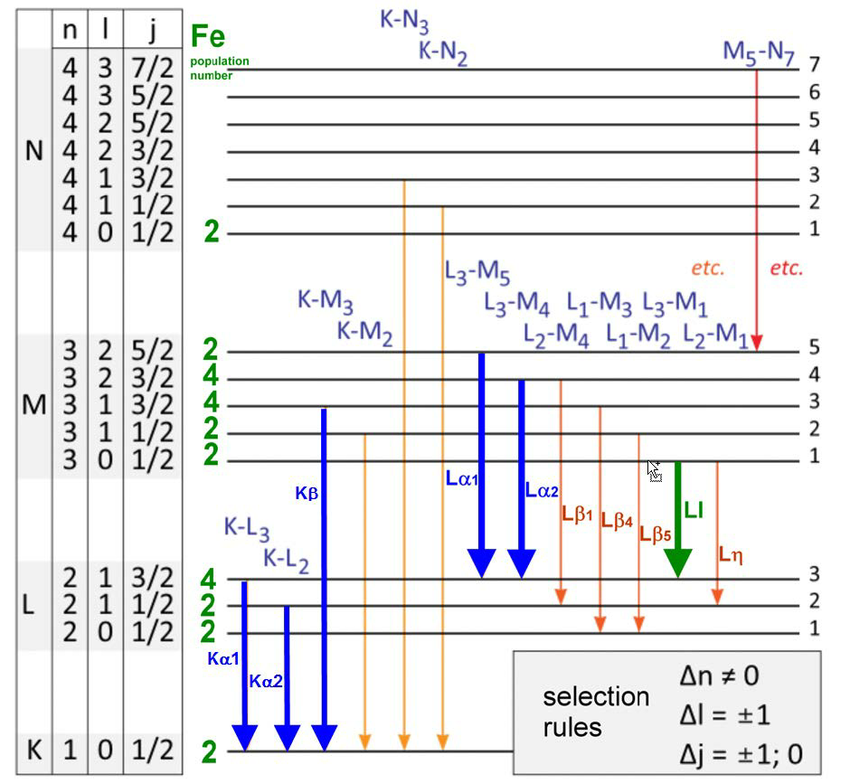
Let’s first get to the basics of atoms, transitions, and energy levels. In very simple terms, an atom is a positively charged nucleus with a number of electrons orbiting it. These electrons typically exist in a number of finite configurations, only one of which is optimally the most stable: the ground state. There are only a finite set of wavelengths of light that an electron within an atom can absorb, and if you strike that electron with a photon of such a wavelength, it will jump: entering a higher energy configuration, or an excited state.
If all other conditions could be ignored, that excited state would spontaneously decay to a lower energy state — either all-at-once to the ground state or in a chain — after a finite amount of time, emitting a photon of a very particular energy (or set of energies) when it does so.
But if you can stimulate a ground-state atom (or a molecular or lattice analogue, with, say, a valence electron) to excite into a particular excited state, you can often coax it to de-excite (and emit radiation) at one particular frequency, very consistently. The big idea of a laser is that you pump energy in, and pretty much every emitted photon that comes out from de-excitations all happen at the same wavelength.
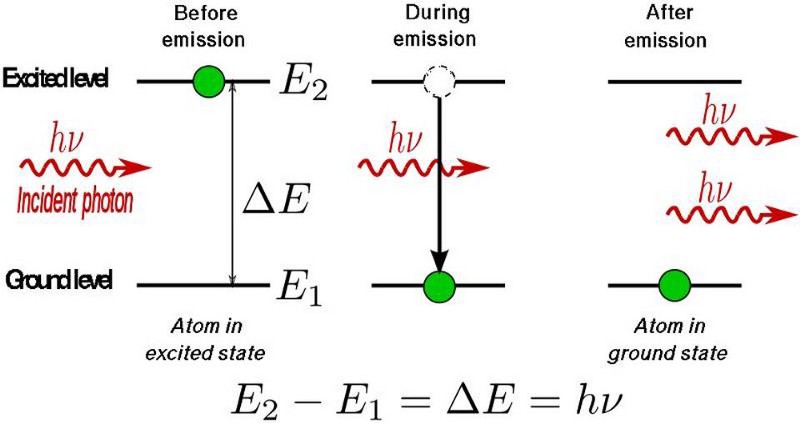
The very idea of a laser itself is still relatively novel, despite how widespread they are. The laser itself was only first invented in 1958. Originally an acronym standing for Light Amplification by Stimulated Emission of Radiation, lasers are a bit of a misnomer. In truth, nothing is really being amplified. They work by taking advantage of the structure of normal matter, which has atomic nuclei and various energy levels for its electrons to occupy. In molecules, crystals, and other bound structures, the particular separations between an electron’s energy levels dictate which transitions are allowed.
The way a laser works is by oscillating the electrons between two allowable states, causing them to emit a photon of a very particular energy when they drop from the higher-energy state to the lower one. The addition of energy, which “pumps” the electrons into those desired excited states, then leads to a spontaneous de-excitation, creating more and more photons of that desired monochromatic frequency. These oscillations are what cause the emission of light. We call them lasers, perhaps, because no one involved thought it was a good idea to use the acronym Light Oscillation by Stimulated Emission of Radiation.

The “spontaneous emission” part, however, is of paramount importance, and what makes a laser, for lack of a better word, lase. If you can produce either multiple atoms-or-molecules in the same excited state and stimulate their spontaneous jump to the ground state, they’ll emit the same energy photon.
These transitions are extremely fast (but aren’t infinitely fast), and so there is a theoretical limit to how quickly you can make a single atom (or molecule) hop up to the excited state and spontaneously emit a photon; the system takes time to reset.
Normally, some type of gas, molecular compound or crystal is used inside a resonant-or-reflective cavity to create a laser, but recent years have uncovered other methods for stimulating this exact type of radiation. Free electrons can also be used to make lasers, as can semiconductors, optical fibers, and possibly even positronium: bound states of electrons and positrons. The wavelength that lasers can emit light in range from extremely long radio waves to incredibly short X-rays, with gamma rays theoretically possible as well. The laser process even occurs naturally in space, at both microwave and visible light frequencies.

As new methods and techniques are developed, the amount of energy lasers produce has continued to rise over time, with intensities limited only by the practicalities of modern technology. In 2018, the Nobel Prize in Physics was awarded for advances in laser technology, with half of the prize going specifically towards controlling the power and pulse frequency of your laser. We think of laser light as being continuously emitted, but that isn’t always necessarily the case. Instead, another option is to save up that laser light you’re producing and to emit all of that energy in a single, short burst. You can either do this all in one go, or you can do it repeatedly, potentially with relatively high frequencies.
In 1985, Nobel Laureates Gérard Mourou and Donna Strickland published an article together where they detailed exactly how they created an ultra-short, high-intensity laser pulse in a repetitive fashion. The amplifying material used was unharmed. The basic setup was four simple-in-principle, but monumental-in-practice, steps:
- First, they created these relatively standard laser pulses.
- Then, they stretched the pulses in time, which reduces their peak power and makes them less destructive.
- Next, they amplified the time-stretched, reduced-power pulses, which the material used for amplification could now survive.
- And finally, they compressed the now-amplified pulses in time.
By making the pulse shorter, more light becomes packed together in the same space, leading to a massive increase in pulse intensity.
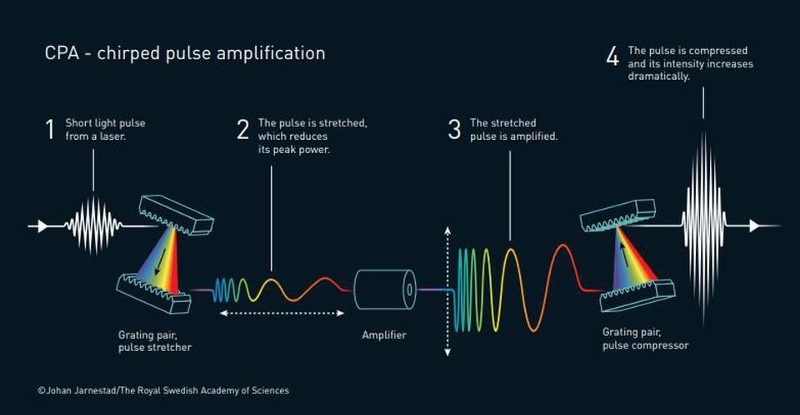
The new technique, known as chirped pulse amplification, became the new standard for high-intensity lasers; it is the technology used in the millions of corrective eye surgeries performed annually. Mourou’s and Strickland’s pioneering work became the basis of Strickland’s Ph.D. thesis, and there are more applications being discovered for their work across a wide variety of fields and industries.
But can those advances continue arbitrarily far into the future, without any bound?
You might wonder if there’s an intrinsic limit to the number of photons that could exist due to a laser (or laser-like process), since there is a limit to, say, the number of electrons you can cram into a given region of space. In quantum mechanics, there’s a very important principle — the Pauli exclusion principle — that declares that no two quantum particles with exactly identical properties can exist in the same quantum state simultaneously.
Only, I omitted a very important caveat: the Pauli exclusion principle only applied to particles like electrons or quarks, whose spin comes in half-integer increments: ±1/2, ±3/2, ±5/2, etc. For particles like photons that possess integer spins: 0, ±1, ±2, etc., there is absolutely no limit to the number of identical particles that can occupy the same quantum state in the same physical location! At a fundamental level, the Pauli exclusion principle is why what we consider “normal matter” takes up space at all. But not everything is bound by that rule, and that includes photons.
The photon, which is the particle produced by lasers of all varieties, has a spin of ±1, and hence you can theoretically pack an arbitrarily large number of them into as small a space as you want.
This is theoretically extremely important, because it means that, if we can figure out the right technology, there’s no limit to the magnitude of energy densities we can achieve with photons. At least, there isn’t a limit that arises due to the Pauli exclusion principle: we can pack an infinite number of photons into an arbitrarily small space. There’s a limit to the intensity a laser can reach: the energy over time on an area. That’s not a fundamental limit, but rather a practical limitation set by the materials used in the laser setup itself.
So let’s imagine, then, that we attempt to do this. We’re going to take a lasing cavity, install mirrors on both ends, and stimulate emitted radiation until we reach the maximum practical intensity for this laser.
Then what we’ll do is make one of the mirrors movable, and slide it inwards, thereby compressing the cavity as we remove the neutral and excited atoms (i.e., the non-photons) inside. This compression, by shrinking the volume in which these photons are present, increases the energy density of the system substantially: the energy density inside that mirrored laser cavity.
If we could do this forever — shrinking the cavity’s volume down as far as we dared — we’d discover that the energy density continued to rise, but also the energy-per-photon would go up too, as the work performed in pulling the mirror inwards (a form of energy) would get transferred into the individual photons. You might imagine, if you continued to pull this mirror in, raising both the overall energy density of the photons and the energy-per-photon in the system, that the energy would rise and rise and rise. Could you perform this task without limit, increasing the energy density and the energy-per-photon as you did it, until you eventually created a black hole?
The answer is no, because there is a fundamental limit in there that we’ll run into first: the energy threshold for producing particle-antiparticle pairs. Once the energy of each individual photon rises above 1.022 MeV, there’s a chance, every time it interacts with another particle (such as by hitting the mirror’s walls), that it will transition from a photon into an electron-positron pair. Once you start producing electrons and positrons, the positrons will start annihilating with the cavity walls and mirrors, blowing your laser apart in a spectacular but catastrophic event.
That’s too bad, because you’d need to reach energies that were much, much higher than that — by about a factor of a sextillion (1021) or so — to create a black hole. At high photon energies, your laser light begins to resemble a matter-antimatter thermal bath, rather than simple coherent light. That limit, as well as (at still higher energies) the fact that individual photons will destroy the cavity boundaries, rather than reflect off of them, will set the ultimate limit as to how energetic lasers within a cavity can get.

That doesn’t mean, however, that we couldn’t engineer as energetic of a laser blast as we like via a clever setup. This could include:
- leveraging large numbers of high-powered lasers all converging on the same point,
- using chirped pulse amplification to achieve zetawatt intensities,
- and shrinking/compressing the pulse to decrease the period while amplifying the power in the process,
or even all of the above.
Everything from laser eye surgeries to fusion blasts at the National Ignition Facility leverages this laser technology, with many of these applications already in use. Practically, yes, there is a limit to the amount of power and the intensity we could ever achieve with a laser. But if we could engineer a material strong enough to withstand a matter-antimatter thermal bath, as well as the highest energy photons imaginable, we could achieve energy densities without an upper limit. Perhaps, someday, this will be the key that unlocks our ability to create a black hole in the laboratory for the very first time!