The ultimate energy limit that lasers will never surpass

- Lasers work by stimulating the emission of radiation within a cavity, over and over, building up as many photons as desired before emitting them.
- It makes one wonder if you could use this technique to build up and produce a virtually limitless amount of energy, potentially all-at-once if desired.
- But it turns out this is not the case at all. There’s a fundamental limit to the amount of energy in lasers, set by an unlikely culprit: the rules of particle physics.
Back in the middle of the 20th century, there was really no good way to create purely monochromatic light: light where every one of the photons that are part of a beam possess precisely the same wavelength. Sure, you could break up white light into its component colors, such as by passing it through a prism or color filter, and selecting for only a narrow range of wavelengths, but that wouldn’t be truly monochromatic. However, the fact that atoms, molecules, lattices, and other structures only admit a specific set of electron transitions brought forth a fascinating possibility: if you could stimulate the same transition (or sets of transitions) over and over, without creating any other transitions in the process, you could produce truly monochromatic light.
Since 1958, we’ve managed to do precisely that with the invention of the laser. Over time, lasers have become more powerful, more widespread, and have been engineered to produce an enormous variety of wavelengths for their emitted light. By having photons of a specific wavelength build up in the lasing cavity, that same-frequency emission gets stimulated over and over again. Many have wondered if you could do this without bound, creating a laser of arbitrarily high energies.
It turns out that the answer is no. You cannot simply build up photons forever to get an arbitrarily large energy density in your laser; once you cross a certain threshold, the laws of physics themselves will stop you. Here’s why there’s an ultimate limit to laser energy, and we’ll never be able to exceed it.
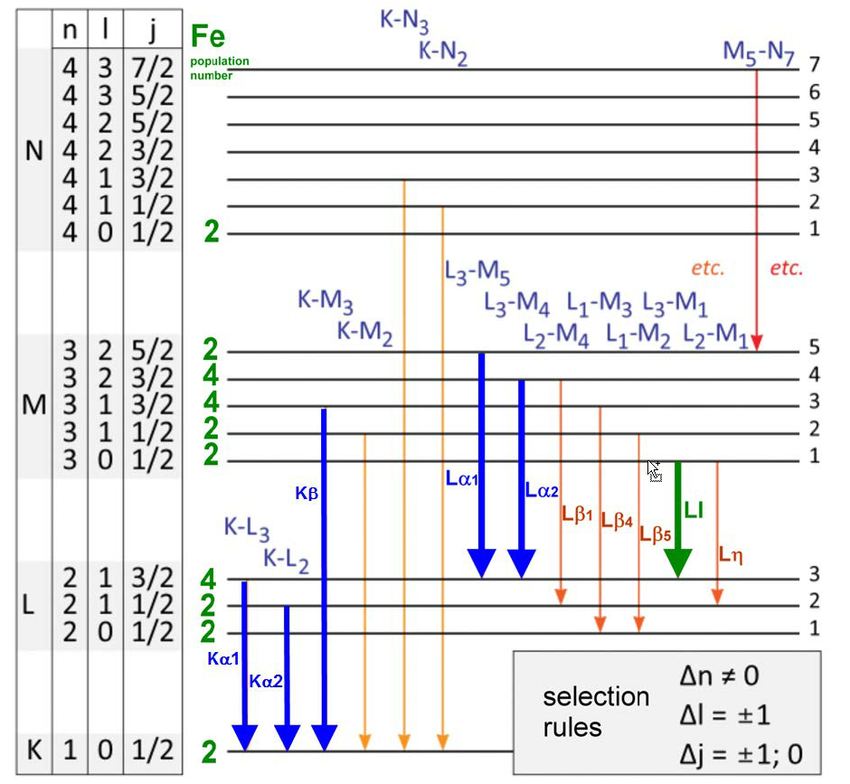
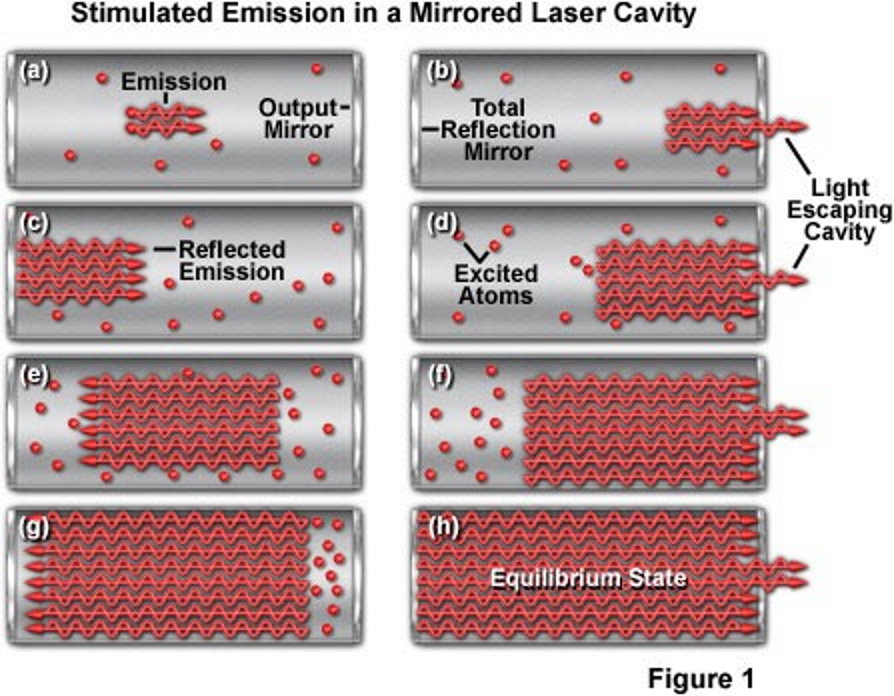
Credit: Daniel Carlos Leite Dias Andrade et al., Conference: 25º CSBMM – Congresso da Sociedade Brasileira de Microscopia e Microanálise, 2015
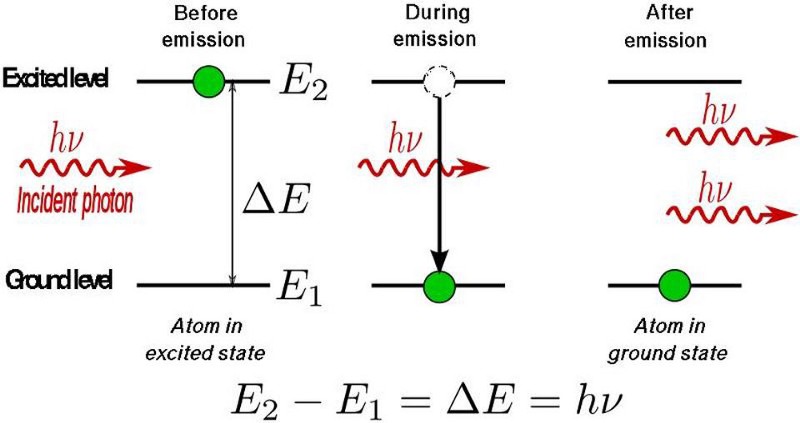
Let’s first get to the basics of atoms, transitions, and energy levels. In very simple terms, an atom is a positively charged nucleus with a number of electrons orbiting it. These electrons typically exist in a number of finite configurations, only one of which is optimally the most stable: the ground state. There is only a finite set of wavelengths of light that an electron within an atom can absorb, and if you strike that electron with a photon of such a wavelength, it will jump: entering a higher energy configuration, or an excited state.
If all other conditions could be ignored, that excited state wouldn’t persist for long, but would instead spontaneously decay to a lower energy state — either all-at-once to the ground state or cascading down a chain of transitions — after a finite amount of time. With each drop-down to a lower energy level, that electron would emit a photon of a very particular energy (or, for multi-photon transitions, a set of energies) when it does so.
However, it’s possible to stimulate a ground-state atom (or a molecular or lattice analogue, with, say, a valence electron) to excite into a particular excited state. The converse is also true: you can often coax an excited atom to de-excite (and emit radiation) at one particular frequency, very consistently. The big idea of a laser is that you pump energy in, and pretty much every emitted photon that comes out from de-excitations all happen at the same wavelength.
The very idea of a laser itself is still relatively novel, despite how widespread they are. The laser was only first invented in 1958. Originally an acronym standing for Light Amplification by Stimulated Emission of Radiation, lasers are a bit of a misnomer. In truth, nothing is really being amplified. Lasers work by taking advantage of the structure of normal matter, which has atomic nuclei and various energy levels for its electrons to occupy. In molecules, crystals, and other bound structures, the particular separations between an electron’s energy levels dictate which transitions are allowed.
The way a laser produces its light is by oscillating the electrons between two allowable states, causing them to emit a photon of a very particular energy when they drop from the higher-energy state to the lower one. The addition of energy, which “pumps” the electrons into those desired excited states, then leads to a spontaneous de-excitation, creating more and more photons of that desired monochromatic frequency. These oscillations, between the excited state and the de-excited state, are what cause the emission of light. We call them lasers, perhaps, because no one involved thought it was a good idea to use the more accurate acronym that describes what’s occurring: Light Oscillation by Stimulated Emission of Radiation.

The “stimulated emission” part, however, is of paramount importance, and what makes a laser, for lack of a better word, lase. If you can produce either multiple atoms-or-molecules in the same excited state and stimulate their spontaneous jump to the ground state, they’ll all emit photons of precisely the same energy, which produces that characteristic monochromatic laser light.
These transitions are extremely fast (but aren’t infinitely fast), and so there is a theoretical limit to how quickly you can make a single atom (or molecule) hop up to the excited state and spontaneously emit a photon. Put simply, the system takes time to reset and be ready for its next oscillation.
Normally, some type of gas, molecular compound or crystal is used inside a resonant-or-reflective cavity to create a laser, but recent years have uncovered other methods for stimulating this exact type of radiation. Free electrons can also be used to make lasers, as can semiconductors, optical fibers, and possibly even positronium: bound states of electrons and positrons. The wavelength in which lasers can emit light ranges from extremely long radio waves to incredibly short X-rays, with gamma rays theoretically possible as well. The laser process even occurs naturally in space, at both microwave and visible light frequencies.

As new methods and techniques are developed, the amount of energy lasers produce has continued to rise over time, with intensities limited only by the practicalities of modern technology. In 2018, the Nobel Prize in Physics was awarded for advances in laser technology, with half of the prize going specifically toward controlling the power and pulse frequency of your laser. Then, in 2023, the Physics Nobel went to the science of attosecond spectroscopy, which also relies on applications of lasers. Although we commonly think of laser light as being continuously emitted, that isn’t always necessarily how it works. Instead, another option is to save up that laser light you’re producing and to emit all of that energy in a single, short burst. You can either do this all in one go, or you can do it repeatedly, potentially with relatively high frequencies.
In 1985, Nobel Laureates Gérard Mourou and Donna Strickland published an article together where they detailed exactly how they created an ultra-short, high-intensity laser pulse in a repetitive fashion. The amplifying material used was unharmed. The basic setup was four simple-in-principle, but monumental-in-practice, steps:
- First, they created these relatively standard laser pulses.
- Then, they stretched the pulses in time, which reduces their peak power and makes them less destructive.
- Next, they amplified the time-stretched, reduced-power pulses, which the material used for amplification could now survive.
- And finally, they compressed the now-amplified pulses in time.
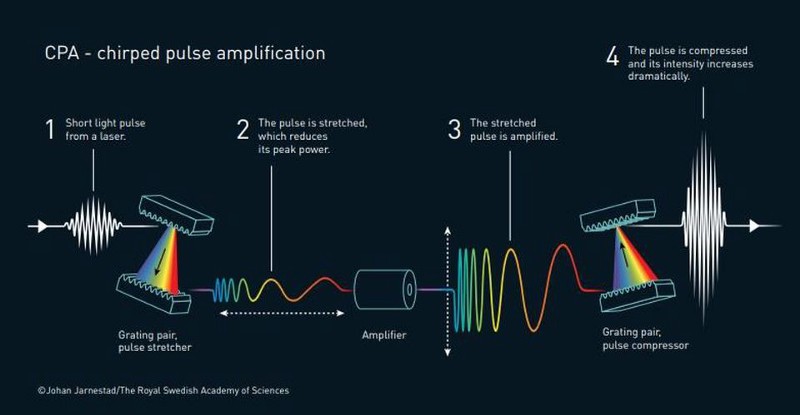
By making the pulse shorter, more light becomes packed together in the same space, leading to a massive increase in pulse intensity. The new technique, known as chirped pulse amplification, became the new standard for high-intensity lasers; it is the technology used in the millions of corrective eye surgeries performed annually. Mourou’s and Strickland’s pioneering work became the basis of Strickland’s Ph.D. thesis, and there are more applications constantly being discovered. Their work now has real-world applications across a wide variety of fields and industries.
But can those advances continue arbitrarily far into the future, without any bound?
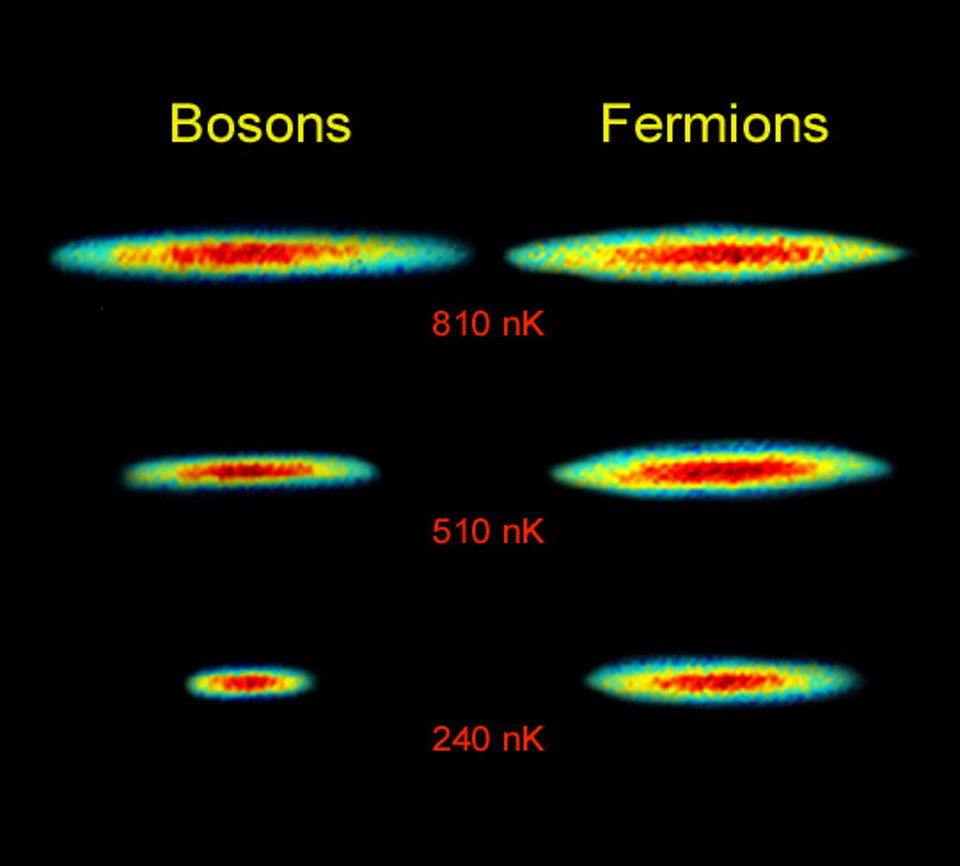
As with most physical processes, there are some fundamental limits that you simply can’t get around. You might wonder, for example, if there’s an intrinsic limit to the number of photons that could exist due to a laser (or laser-like process), since there is a limit to, say, the number of electrons you can cram into a given region of space. In quantum mechanics, there’s a very important principle — the Pauli exclusion principle — that declares that no two quantum particles with exactly identical properties can exist in the same quantum state simultaneously.
Only, I omitted a very important caveat: the Pauli exclusion principle doesn’t apply to all particles! It only applies to particles like electrons or quarks, whose spin comes in half-integer increments: ±1/2, ±3/2, ±5/2, etc. For particles like photons that possess integer spins: 0, ±1, ±2, etc., there is absolutely no limit to the number of identical particles that can occupy the same quantum state in the same physical location! At a fundamental level, the Pauli exclusion principle is why what we consider “normal matter” takes up space at all. But not everything is bound by such an exclusion rule, and the bosonic photon, the particle of light, doesn’t obey it at all.
The photon, which is the particle produced by lasers of all varieties, has a spin of ±1, and hence you can theoretically pack an arbitrarily large number of them into as small a space as you want.
This is theoretically extremely important, because it means that, if we can figure out the right technology, there’s no limit to the magnitude of energy densities we can achieve with photons. Or rather, there isn’t a limit that arises due to the Pauli exclusion principle itself, as we can pack an infinite number of photons into an arbitrarily small space. There are limits to the system, however, such as a limit to the intensity a laser can reach: the energy over time acting on an area. That’s not a fundamental limit, but rather a practical limitation set by the materials used in the laser setup itself.
So let’s imagine, then, that we attempt to create the most energetic laser of all-time. We’re going to take a lasing cavity, install mirrors on both ends, and stimulate emitted radiation until we reach the maximum practical intensity for this laser. Then what we’ll do is make one of the mirrors movable, and slide it inward, thereby compressing the cavity as we remove the neutral and excited atoms (i.e., the non-photons) inside. This compression, by shrinking the volume in which these photons are present, increases the energy density of the system substantially: the energy density inside that mirrored laser cavity.
If we could do this forever — shrinking the cavity’s volume down as far as we dared — we’d discover that the energy density continued to rise, but also the energy-per-photon would go up too, as the work performed in pulling the mirror inward (a form of energy) would get transferred into the individual photons. You might imagine, if you continued to pull this mirror in, raising both the overall energy density of the photons and the energy-per-photon in the system, that the energy would rise and rise and rise.
Now we come to the critical question: could you perform this task without limit, increasing the energy density and the energy-per-photon as you did it, until you eventually created a black hole?
The answer is no, because there is a fundamental limit in there that we’ll run into first: the energy threshold for producing particle-antiparticle pairs. Once the energy of each individual photon rises above 1.022 MeV, there’s a chance, every time it interacts with another particle (such as by hitting the mirror’s walls), that this photon will transition from being a photon into being an electron-positron pair. Once you start producing electrons and positrons, the positrons will start annihilating with the cavity walls and mirrors, blowing your laser apart in a spectacular but catastrophic event.
Although this might seem incredibly energetic, that 1.022 MeV of energy is only huge when we talk about it for a single photon, representing a photon of gamma-ray energies (something that normally only happens when nuclear transitions emit them). Still, that energy is hundreds of thousands of times smaller than the highest-energy gamma-rays we can create under laboratory conditions.
And that’s too bad, because if you had dreamed of using lasers to create a black hole, you’d find that you were completely out of luck. You’d require energies that were much, much higher than that — by about a factor of a sextillion (1021) or so — to create a black hole. At high photon energies, your laser light begins to resemble a matter-antimatter thermal bath, rather than simple coherent light. That limit, as well as (at still higher energies) the fact that individual photons will destroy the cavity boundaries, rather than reflect off of them, will set the ultimate limit as to how energetic lasers within a cavity can get.

That doesn’t mean, however, that we couldn’t engineer as energetic of a one-time, temporary laser blast as we like via a clever setup. This could include:
- leveraging large numbers of high-powered lasers whose beams all converge on the same point,
- using chirped pulse amplification to achieve zetawatt (or greater) intensities, albeit for minuscule fractions of a second,
- and shrinking/compressing the pulse to decrease the period while amplifying the power in the process.
Using all of the aforementioned techniques, together, could potentially smash the record for the most energetic laser ever created on Earth, or for that matter, anywhere in the Universe.
Everything from laser eye surgeries to fusion blasts at the National Ignition Facility leverages this laser technology, with many lasers already having found a place in highly useful applications. Practically, yes, there is a limit to the amount of power and the intensity we could ever achieve with a laser. But if we could engineer a material strong enough to withstand a matter-antimatter thermal bath, and could reflect the light efficiently from the highest energy photons imaginable, we could achieve energy densities without an upper limit.
Perhaps, someday, lasers will be the key that unlocks our ability to create a black hole in the laboratory for the very first time!
This article was first published in September of 2022. It was updated in August of 2025.