Is Theoretical Physics Wasting Our Best Living Minds On Nonsense?
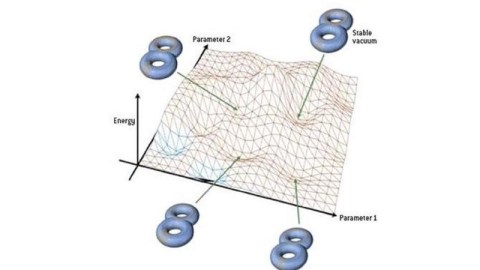
There’s no such thing as a theory that’s too beautiful to be wrong, if it doesn’t agree with experiment.
The history of physics is filled with great ideas that you’ve heard of, like the Standard Model, the Big Bang, General Relativity, and so on. But it’s also filled with brilliant ideas that you probably haven’t heard of, like the Sakata Model, Technicolor theory, the Steady State Model. and Plasma Cosmology. Today, we have theories that are highly fashionable, but without any evidence for them: supersymmetry, grand unification, string theory, and the multiverse.
Because of the way the field is structured, mired in a sycophancy of ideas, careers in theoretical high-energy physics that focus on these topics are often successful. On the other hand, choosing other topics means going it alone. The idea of “beauty” or “naturalness” has been a guiding principle in physics for a long time, and has led us to this point. In her new book, Lost In Math, Sabine Hossenfelder convincingly argues that continuing to adhere to this principle is exactly what’s leading us astray.

Imagine you were given a hypothetical problem of picking two billionaires off of a list, and estimating the difference in their net worths. Imagine they’re anonymous, and that you won’t know which one is worth more, where they rank on the Forbes billionaires list, or how much either one is actually worth at the moment.
We can call the first one A, the second one B, and the difference between them C, where A — B = C. Even without any other knowledge about them, there’s one important thing you can state about C: it’s very unlikely that it will be much, much smaller than A or B. In other words, if A and B are both in the billions of dollars, then it’s likely that C will be in the billions, too, or at least in the hundreds of millions.
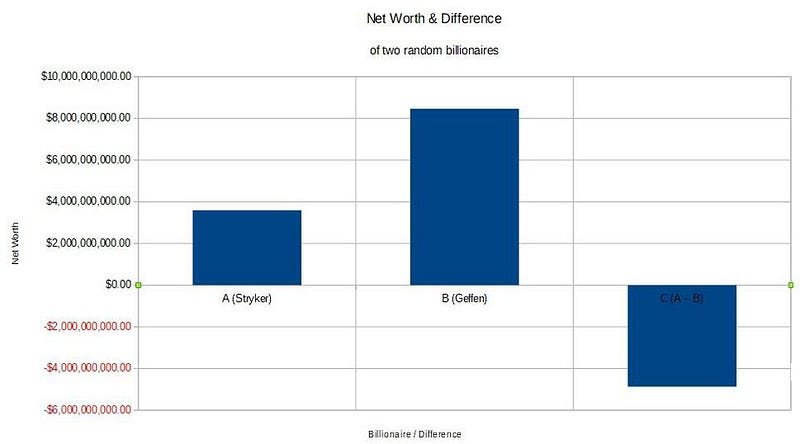
For example, A might be Pat Stryker (#703 on the list), worth, let’s say, $3,592,327,960. And B might be David Geffen (#190), worth $8,467,103,235. The difference between them, or A — B, is then -$4,874,775,275. C has a 50/50 shot of being positive or negative, but in most cases, it’s going to be of the same order of magnitude (within a factor of 10 or so) of both Aand B.
But it won’t always be. For example, most of the over 2,200 billionaires in the world are worth less than $2 billion, and there are hundreds worth between $1 billion and $1.2 billion. If you happened to pick two of them at random, it wouldn’t surprise you terribly if the difference in their net worth was only a few tens of millions of dollars.

It might, however, surprise you if the difference between them was only a few thousand dollars, or was zero. “How unlikely,” you’d think. But it might not be all that unlikely after all.
After all, you don’t know which billionaires were on your list. Would you be shocked to learn the Winklevoss twins — Cameron and Tyler, the first Bitcoin billionaires — had identical net worths? Or that the Collison brothers, Patrick and John (co-founders of Stripe), were worth the same amount to within a few hundred dollars?
No. This wouldn’t be surprising, and it exposes a truth about large numbers: in general if A is large and B is large, then A – B will also be large… but it won’t be if there’s some reason that A and B are very close together. The distribution of billionaires isn’t completely random, you see, and so there might be some underlying reason for these two seemingly unrelated things to actually be related. (In the case of the Collisons or Winklevosses, literally!)
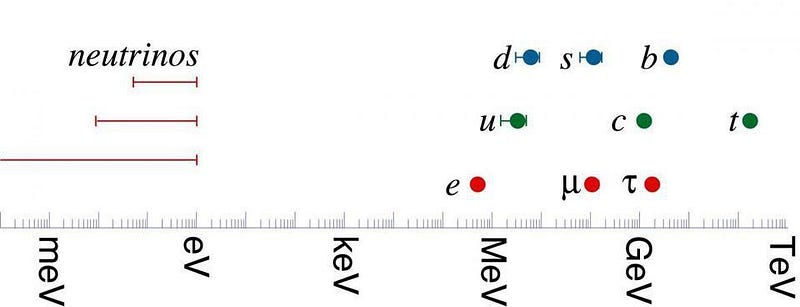
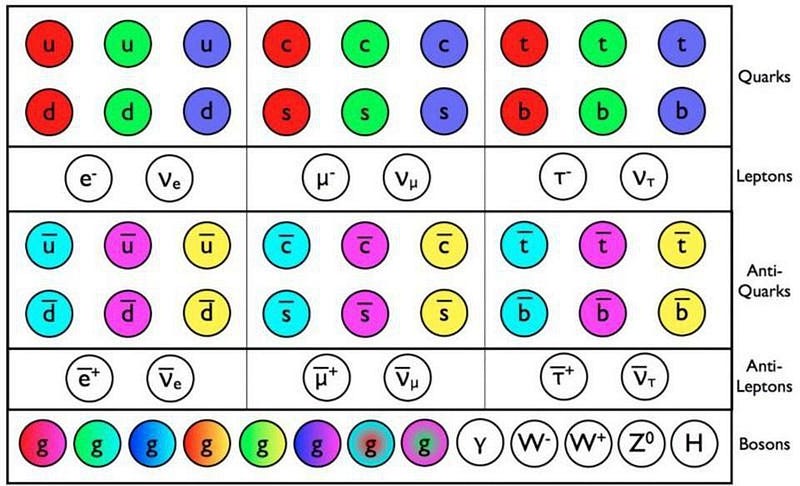
This same property is true in physics. The electron, the lightest particle that makes up the atoms we find on Earth, is more than 300,000 times less massive than the top quark, the heaviest Standard Model particle. The neutrinos are at least four million times lighter than the electron, while the Planck mass — the so-called “natural” energy scale for the Universe — is some 10¹⁷ (or 100,000,000,000,000,000) times heavier than the top quark.
If you weren’t aware of any underlying reason why these masses should be so different, you’d assume there was some reason for it. And maybe there is one. This type of thinking is known as a fine-tuning or “naturalness” argument. In its simplest form, it states that there ought to be some sort of physical explanation for why components of the Universe with very different properties ought to have those differences between them.
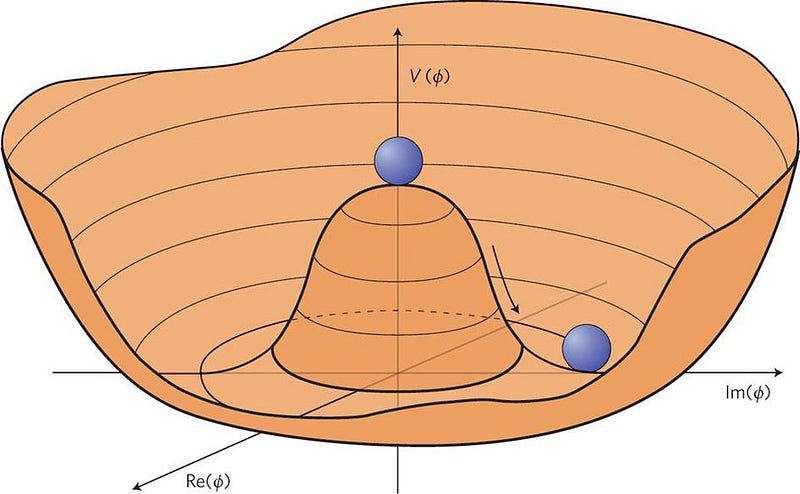
In the 20th century, physicists used naturalness arguments to great effect. One way to explain great differences in scale is to impose a symmetry at high energies, and then to study the consequences of breaking it at a lower energy. A number of great ideas came out of this reasoning, particularly in the field of particle physics. The gauge bosons in the electroweak force came about from this line of thought, as did the Higgs mechanism and, as was confirmed just a few years ago, the Higgs boson. The entire Standard Model was built on these types of symmetries and naturalness arguments, and nature happened to agree with our best theories.
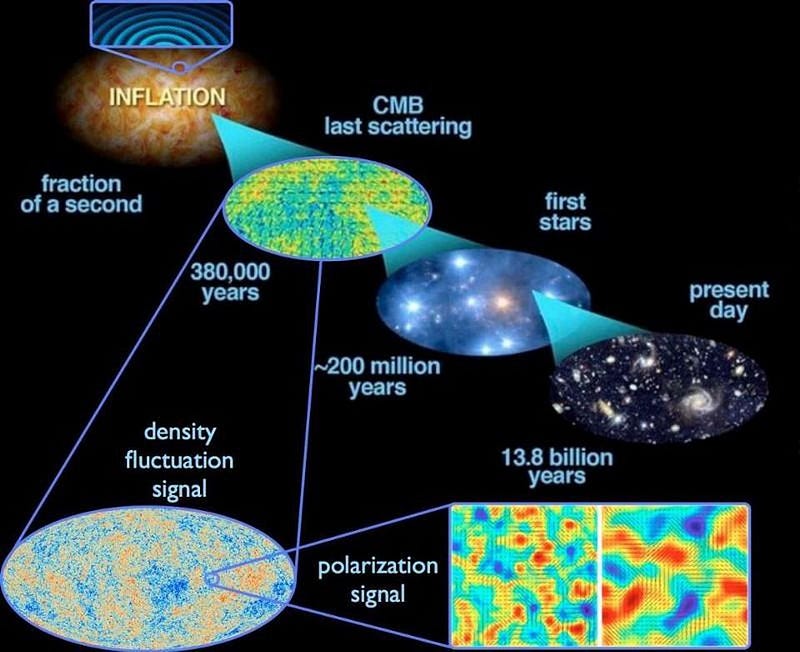
Another great success was cosmic inflation. The Universe needed to have been finely-tuned to a great degree in the early stages to produce the Universe we see today. The balance between the expansion rate, the spatial curvature, and the amount of matter-and-energy within it must have been extraordinary; it appears to be unnatural. Cosmic inflation was a proposed mechanism to explain it, and has since had many of its predictions confirmed, such as:
- a nearly scale-invariant spectrum of fluctuations,
- the existence of super-horizon overdensities and underdensities,
- with density imperfections that are adiabatic in nature,
- and an upper limit to the temperature reached in the early, post-Big Bang Universe.
But despite the successes of these naturalness arguments, they don’t always bear fruit.
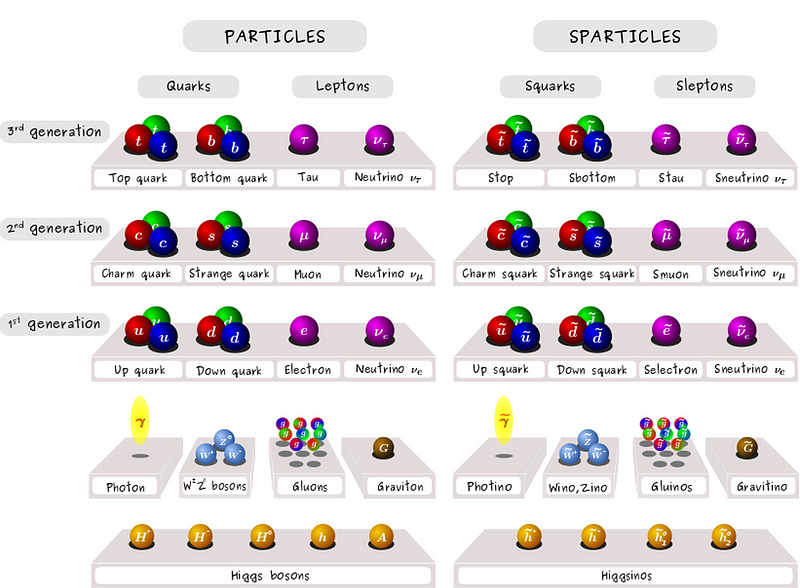
There’s an unnaturally small amount of CP-violation in the strong decays. The proposed solution (a new symmetry known as the Peccei-Quinn symmetry) have had zero of its new predictions confirmed. The difference in mass scale between the heaviest particle and the Planck scale (the hierarchy problem) was the motivation for supersymmetry; again, it’s had zero of its predictions confirmed. The unnaturalness of the Standard Model has led to new symmetries in the form of Grand Unification and, more recently, String Theory, which (again) have had none of their predictions confirmed. And the unnaturally low-but-non-zero value of the cosmological constant has led to the predictions of a specific type of multiverse that cannot even be tested. This too, of course, is unconfirmed.
Yet unlike in the past, these dead-ends continue to represent the fields in which the leading theorists and experimentalists cluster to investigate. These blind alleys, which have borne no fruit for literally two generations of physicists, continue to attract funding and attention, despite possibly being disconnected from reality completely. In her new book, Lost In Math, Sabine Hossenfelder adroitly confronts this crisis head on, interviewing mainstream scientists, Nobel Laureates, and (non-crackpot) contrarians alike. You can feel her frustration, and also the desperation of many of the people she speaks with. The book answers the question of “have we let wishful thinking about what secrets nature holds cloud our judgment?” with a resounding “yes!”
The book is a wild, deep, thought-provoking read that would make any reasonable person in the field who’s still capable of introspection doubt themselves. No one likes confronting the possibility of having wasted their lives chasing a phantasm of an idea, but that’s what being a theorist is all about. You see a few pieces of an incomplete puzzle and guess what the full picture truly is; most times, you’re wrong. Perhaps, in these cases, all our guesses have been wrong. In my favorite exchange, she interviews Steven Weinberg, who draws on his vast experience in physics to explain why naturalness arguments are good guides for theoretical physicists. But he only manages to convince us that they were good ideas for the classes of problems they previously succeeded at solving. There’s no guarantee they’ll be good guideposts for the current problems; in fact, they demonstrably have not been.

If you are a theoretical particle physicist, a string theorist, or a phenomenologist — particularly if you suffer from cognitive dissonance — you will not like this book. If you are a true believer in naturalness as the guiding light of theoretical physics, this book will irritate you tremendously. But if you’re someone who isn’t afraid to ask that big question of “are we doing it all wrong,” the answer might be a big, uncomfortable “yes.” Those of us who are intellectually honest physicists have been living with this discomfort for many decades now. In Sabine’s book, Lost In Math, this discomfort is now made accessible to the rest of us.
* — Full disclosure: Ethan Siegel received a review copy of Lost In Math at no charge.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.




