How To Prove Einstein’s Relativity In The Palm Of Your Hand

Particle physics is everywhere, even in the palm of your hand.

When you hold out your palm and point it towards the sky, what is it that’s interacting with your hand? You might correctly surmise that there are ions, electrons and molecules all colliding with your hand, as the atmosphere is simply unavoidable here on Earth. You might also remember that photons, or particles of light, must be striking you, too.

But there’s something more striking your hand that, without relativity, simply wouldn’t be possible. Every second, approximately one muon — the unstable, heavy cousin of the electron — passes through your outstretched palm. These muons are made in the upper atmosphere, created by cosmic rays. With a mean lifetime of 2.2 microseconds, you might think the ~100+ km journey to your hand would be impossible. Yet relativity makes it so, and the palm of your hand can prove it. Here’s how.

*While cosmic ray showers are common from high-energy particles, it’s mostly the muons which make it down to Earth’s surface, where they are detectable with the right setup.* (ALBERTO IZQUIERDO; COURTESY OF FRANCISCO BARRADAS SOLAS)

Individual, subatomic particles are almost always invisible to human eyes, as the wavelengths of light we can see are unaffected by particles passing through our bodies. But if you create a pure vapor made out of 100% alcohol, a charged particle passing through it will leave a trail that can be visually detected by even as primitive an instrument as the human eye.

As a charged particle moves through the alcohol vapor, it ionizes a path of alcohol particles, which act as centers for the condensation of alcohol droplets. The trail that results is both long enough and long-lasting enough that human eyes can see it, and the speed and curvature of the trail (if you apply a magnetic field) can even tell you what type of particle it was.

This principle was first applied in particle physics in the form of a cloud chamber.

A completed cloud chamber can be built in a day out of readily-available materials and for less than $100. You can use it to prove the validity of Einstein’s relativity, if you know what you’re doing! (INSTRUCTABLES USER EXPERIENCINGPHYSICS)

Today, a cloud chamber can be built, by anyone with commonly available parts, for a day’s worth of labor and less than $100 in parts. (I’ve published a guide here.) If you put the mantle from a smoke detector inside the cloud chamber, you’ll see particles emanate from it in all directions and leave tracks in your cloud chamber.

That’s because a smoke detector’s mantle contains radioactive elements such as Americium, which decays by emitting α-particles. In physics, α-particles are made up of two protons and two neutrons: they’re the same as a helium nucleus. With the low energies of the decay and the high mass of the α-particles, these particles make slow, curved tracks and can even be occasionally seen bouncing off of the cloud chamber’s bottom. It’s an easy test to see if your cloud chamber is working properly.

For an extra bonus of radioactive tracks, add the mantle of a smoke detector to the bottom of your cloud chamber, and watch the slow-moving particles emanating outward from it. Some will even bounce off the bottom! (NASA/GRC/BILL BOWLES)

If you build a cloud chamber like this, however, those α-particle tracks aren’t the only things you’ll see. In fact, even if you leave the chamber completely evacuated (i.e., you don’t put a source of any type inside or nearby), you’ll still see tracks: they’ll be mostly vertical and appear to be perfectly straight.

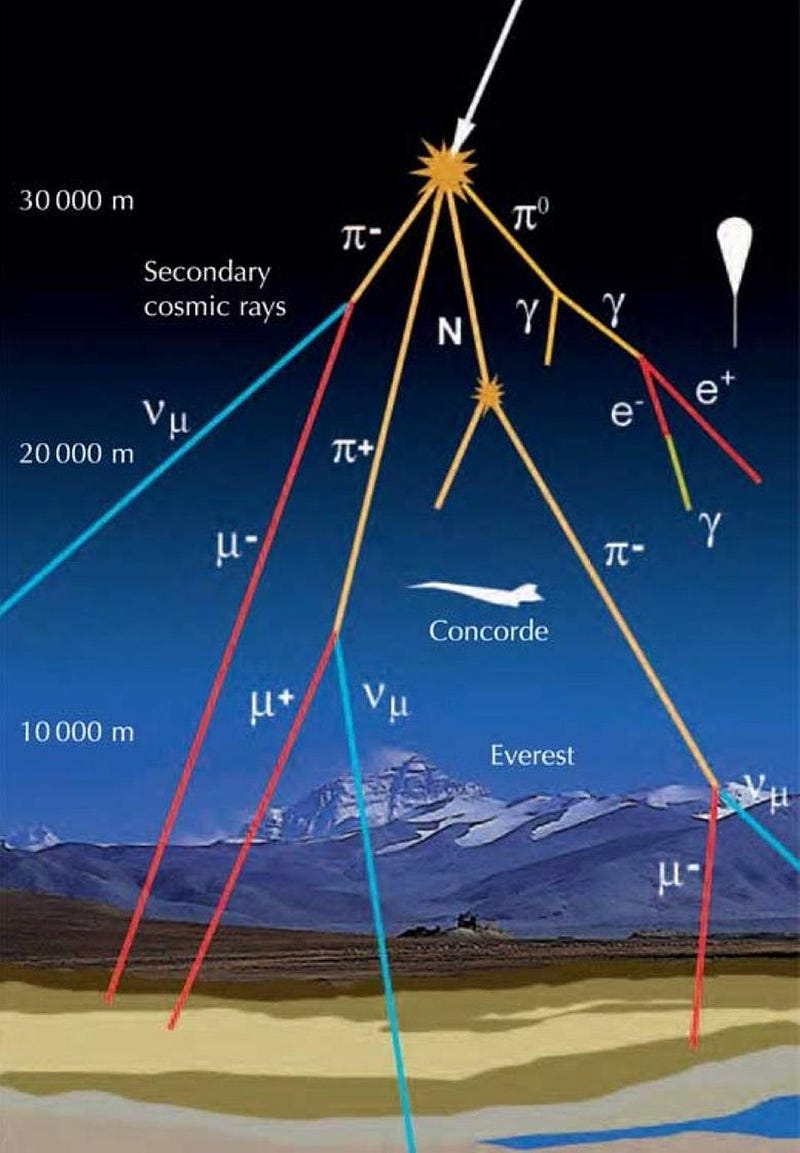
This is because of cosmic rays: high-energy particles that strike the top of Earth’s atmosphere, producing cascading particle showers. Most of the cosmic rays are made up of protons, but move with a wide variety of speeds and energies. The higher-energy particles will collide with particles in the upper atmosphere, producing particles like protons, electrons, and photons, but also unstable, short-lived particles like pions. These particle showers are a hallmark of fixed-target particle physics experiments, and they occur naturally from cosmic rays, too.

Although there are four major types of particles that can be detected in a cloud chamber, the long and straight tracks are the cosmic ray muons, which can be used to prove that special relativity is correct. (WIKIMEDIA COMMONS USER CLOUDYLABS)

The thing about pions is that they come in three varieties: positively charged, neutral, and negatively charged. When you make a neutral pion, it just decays into two photons on very short (~10–16 s) timescales. But charged pions live longer (for around 10–8 s) and when they decay, they primarily decay into muons, which are point particles like electrons but have 206 times the mass.

Muons also are unstable, but they’re the longest-lived unstable fundamental particle as far as we know. Owing to their relatively small mass, they live for an astoundingly long 2.2 microseconds, on average. If you were to ask how far a muon could travel once created, you might think to multiply its lifetime (2.2 microseconds) by the speed of light (300,000 km/s), getting an answer of 660 meters. But that leads to a puzzle.

Cosmic ray shower and some of the possible interactions. Note that if a charged pion (left) strikes a nucleus before it decays, it produces a shower, but if it decays first (right), it produces a muon that will reach the surface. (KONRAD BERNLÖHR OF THE MAX-PLANCK-INSTITUTE AT HEIDELBERG)

I told you earlier that if you hold out the palm of your hand, roughly one muon per second passes through it. But if they can only live for 2.2 microseconds, they’re limited by the speed of light, and they’re created in the upper atmosphere (around 100 km up), how is it possible for those muons to reach us?

You might start to think of excuses. You might imagine that some of the cosmic rays have enough energy to continue cascading and producing particle showers during their entire journey to the ground, but that’s not the story the muons tell when we measure their energies: the lowest ones are still created some 30 km up. You might imagine that the 2.2 microseconds is just an average, and maybe the rare muons that live for 3 or 4 times that long will make it down. But when you do the math, only 1-in-1050 muons would survive down to Earth; in reality, nearly 100% of the created muons arrive.

A light-clock, formed by a photon bouncing between two mirrors, will define time for any observer. Although the two observers may not agree with one another on how much time is passing, they will agree on the laws of physics and on the constants of the Universe, such as the speed of light. When relativity is applied correctly, their measurements will be found to be equivalent to one another, as the correct relativistic transformation will allow one observer to understand the observations of the other. (JOHN D. NORTON)

How can we explain such a discrepancy? Sure, the muons are moving close to the speed of light, but we’re observing them from a reference frame where we’re stationary. We can measure the distance the muons travel, we can measure the time they live for, and even if we give them the benefit of the doubt and say that they’re moving at (rather than near) the speed of light, they shouldn’t even make it for 1 kilometer before decaying.

But this misses one of the key points of relativity! Unstable particles don’t experience time as you, an external observer, measures it. They experience time according to their own onboard clocks, which will run slower the closer they move to the speed of light. Time dilates for them, which means that we will observe them living longer than 2.2 microseconds from our reference frame. The faster they move, the farther we’ll see them travel.

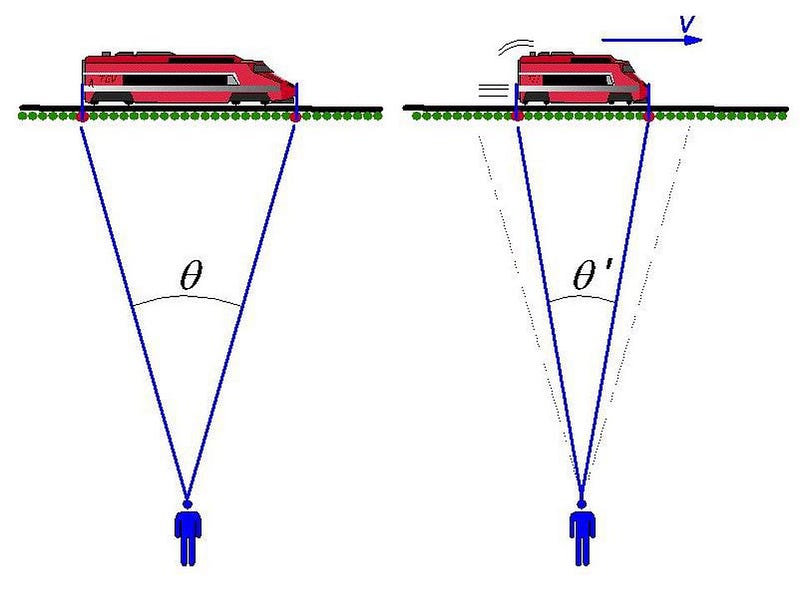
One revolutionary aspect of relativistic motion, put forth by Einstein but previously built up by Lorentz, Fitzgerald, and others, that rapidly moving objects appeared to contract in space and dilate in time. The faster you move relative to someone at rest, the greater your lengths appear to be contracted, while the more time appears to dilate for the outside world. This picture, of relativistic mechanics, replaced the old Newtonian view of classical mechanics, and can explain the lifetime of a cosmic ray muon. (CURT RENSHAW)

How does this work out for the muon? From its reference frame, time passes normally, so it will only live for 2.2 microseconds according to its own clocks. But it will experience reality as though it hurtles towards Earth’s surface extremely close to the speed of light, causing lengths to contract in its direction of motion.

If a muon moves at 99.999% the speed of light, every 660 meters outside of its reference frame will appear as though it’s just 3 meters in length. A journey of 100 km down to the surface would appear to be a journey of 450 meters in the muon’s reference frame, taking up just 1.5 microseconds of time according to the muon’s clock.

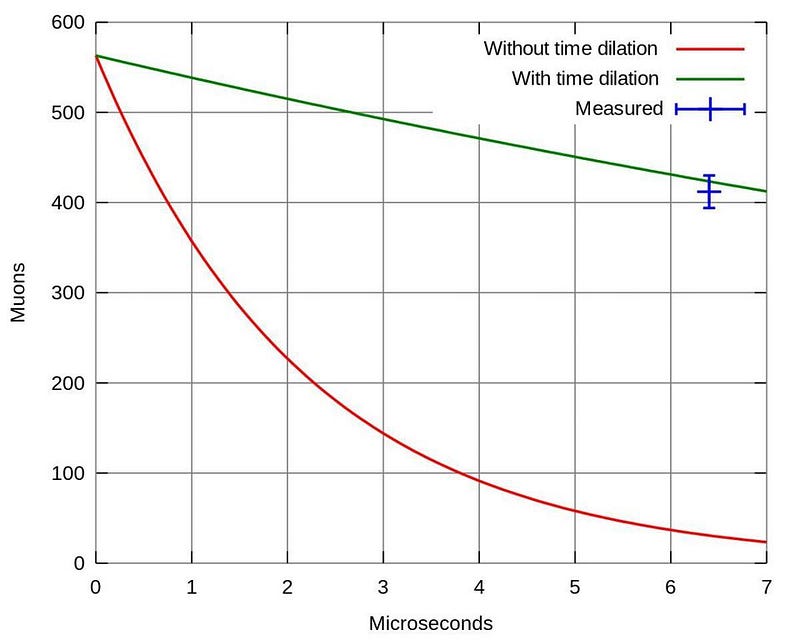
*At high enough energies and velocities, relativity becomes important, allowing many more muons to survive than would without the effects of time dilation.* (FRISCH/SMITH, AM. J. OF PHYS. 31 (5): 342–355 (1963) / WIKIMEDIA COMMONS USER D.H)

This teaches us how to reconcile things for the muon: from our reference frame here on Earth, we see the muon travel 100 km in a timespan of about 4.5 milliseconds. This is just fine, because time is dilated for the muon and lengths are contracted for it: it sees itself as traveling 450 meters in 1.5 microseconds, and hence it can remain alive all the way down to its destination of Earth’s surface.

Without the laws of relativity, this cannot be explained! But at high velocities, which correspond to high particle energies, the effects of time dilation and length contraction enable not just a few but mostof the created muons to survive. This is why, even all the way down here at the surface of the Earth, one muon per second still appears to pass through your upturned, outstretched hand.

The V-shaped track in the center of the image arises from a muon decaying to an electron and two neutrinos. The high-energy track with a kink in it is evidence of a mid-air particle decay. By colliding positrons and electrons at a specific, tunable energy, muon-antimuon pairs could be produced at will. The necessary energy for making a muon/antimuon pair from high-energy positrons colliding with electrons at rest is almost identical to the energy from electron/positron collisions necessary to create a Z-boson. (THE SCOTTISH SCIENCE & TECHNOLOGY ROADSHOW)

If you ever doubted relativity, it’s hard to fault you: the theory itself seems so counterintuitive, and its effects are thoroughly outside the realm of our everyday experience. But there is an experimental test you can perform right at home, cheaply and with just a single day’s efforts, that allow you see the effects for yourself.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

You can build a cloud chamber, and if you do, you will see those muons. If you installed a magnetic field, you’d see those muon tracks curve according to their charge-to-mass ratio: you’d immediately know they weren’t electrons. On rare occasion, you’d even see a muon decaying in mid-air. And, finally, if you measured their energies, you’d find that they were moving ultra-relativistically, at 99.999%+ the speed of light. If not for relativity, you wouldn’t see a single muon at all.

Time dilation and length contraction are real, and the fact that muons survive, from cosmic ray showers all the way down to Earth, prove it beyond a shadow of a doubt.

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.