How Far Could A Spaceship Go If We Never Ran Out Of Thrust?

A single lifetime is more than enough to take you to the limits of the Universe.
Right now, there are only three things limiting how far our spacecrafts can take us in the Universe: the resources we devote to it, the constraints of our existing technology, and the laws of physics. If we were willing to devote more resources to it as a society, we have the technological know-how right now to take human beings to any of the known planets or moons within the Solar System, but not to any objects in the Oort cloud or beyond. Crewed space travel to another star system, at least with the technology we have today, is still a dream for future generations.
But if we could develop superior technology — nuclear-powered rockets, fusion technology, matter-antimatter annihilation, or even dark matter-based fuel — the only limits would be the laws of physics. Sure, if physics works as we understand it today, traversable wormholes might not be in the cards. We might not be able to fold space or achieve warp drive. And the limitations of Einstein’s relativity, preventing us from teleporting or traveling faster than light, might not ever be overcome. Even without invoking any new physics, we’d be able to travel surprisingly far in the Universe, reaching any object presently less than 18 billion light-years away. Here’s how we’d get there.

When we take a look at conventional rockets that we launch from Earth, it surprises most people to learn that they barely accelerate more rapidly than gravity accelerates us here on Earth. If we were to jump or drop from a high altitude, Earth’s gravity would accelerate us towards our planet’s center at 9.8 m/s² (32 ft/s²). For every second that passes by while we’re in free-fall, so long as we neglect outside forces like air resistance, our speed increases in the downward direction by an additional 9.8 m/s (32 ft/s).
The acceleration that we experience due to Earth’s gravity is known as “1g” (pronounced “one gee”), which exerts a force on all objects equal to our mass times that acceleration: Newton’s famous F = ma. What makes our rockets so special is not that they accelerate at approximately this rate, as many objects like cars, bullets, railguns, and even roller coasters frequently and easily surpass it. Rather, rockets are special because they sustain this acceleration for long periods of time in the same direction, enabling us to break the bonds of gravity and achieve escape velocity from Earth.

One of the greatest challenges facing human beings who wish to take long-term journeys in space is the biological effects of not having Earth’s gravity. Earth’s gravity is required for healthy development and maintenance of a human body, with our bodily functions literally failing us if we spend too long in space. Our bone densities drop; our musculature atrophies in significant ways; we experience “space blindness;” and even the International Space Station astronauts who are most diligent about doing hours of exercise a day for months are unable to support themselves for more than a few steps upon returning to Earth.
One way that challenge could be overcome is if we could sustain an acceleration of 1g not for a few minutes, propelling us into space, but continuously. A remarkable prediction of Einstein’s relativity — verified experimentally many times over — is that all objects in the Universe can detect no difference between a constant acceleration and an acceleration due to gravity. If we could keep a spacecraft accelerating at 1g, there would be no physiological difference experienced by an astronaut on board that spacecraft as compared with a human in a stationary room on Earth.

It takes a leap of faith to presume that we might someday be able to achieve constant accelerations indefinitely, as that would necessitate having a limitless supply of fuel at our disposal. Even if we mastered matter-antimatter annihilation — a 100% efficient reaction — we are limited by the fuel we can bring on board, and we’d quickly hit a point of diminishing returns: the more fuel you bring, the more fuel you need to accelerate not only your spacecraft, but all the remaining fuel that’s on board as well.
Still, there are many hopes that we could gather material for fuel on our journey. Ideas have included using a magnetic field to “scoop” charged particles into a rocket’s path, providing particles and antiparticles that could then be annihilated for propulsion. If dark matter turns out to be a specific type of particle that happens to be its own antiparticle — much like the common photon — then simply collecting it and annihilating it, if we could master that type of manipulation, could successfully supply a traveling spacecraft with all the fuel it needs for constant acceleration.

If it weren’t for Einstein’s relativity, you might think that, with each second that passes by, you’d simply increase your speed by another 9.8 m/s. If you started off at rest, it would only take you a little less than a year — about 354 days — to reach the speed of light: 299,792,458 m/s. Of course, that’s a physical impossibility, as no massive object can ever reach, much less exceed, the speed of light.
The way this would play out, in practice, is that your speed would increase by 9.8 m/s with each second that goes by, at least, initially. As you began to get close to the speed of light, reaching what physicists call “relativistic speeds” (where the effects of Einstein’s relativity become important), you’d start to experience two of relativity’s most famous effects: length contraction and time dilation.
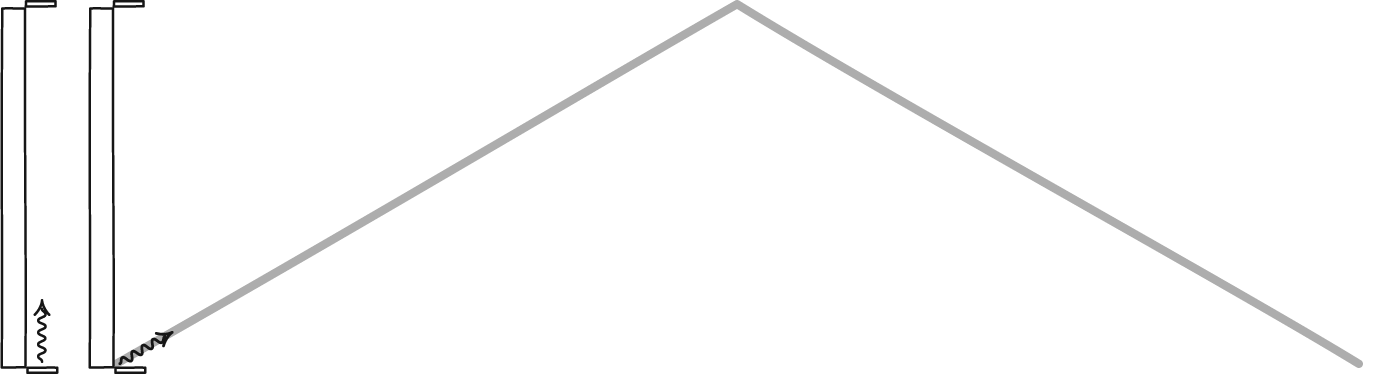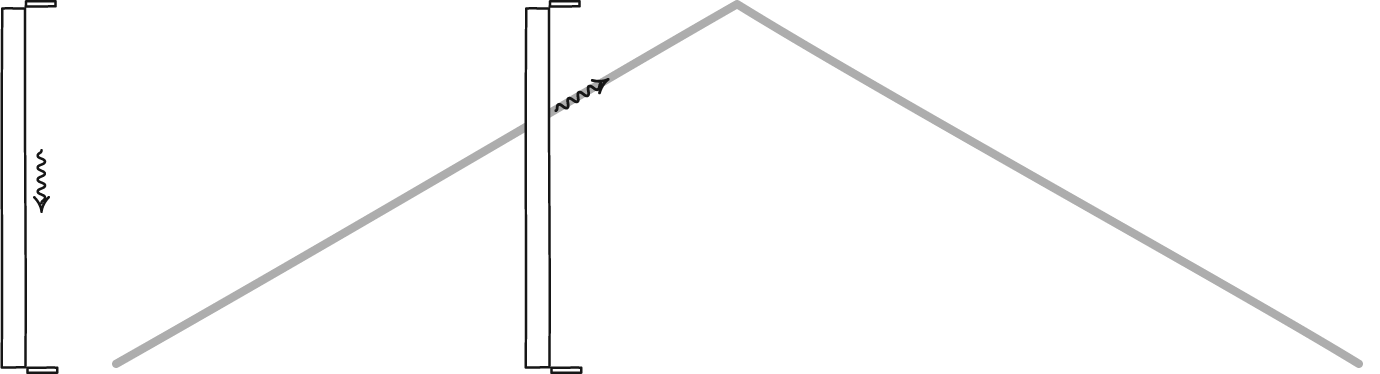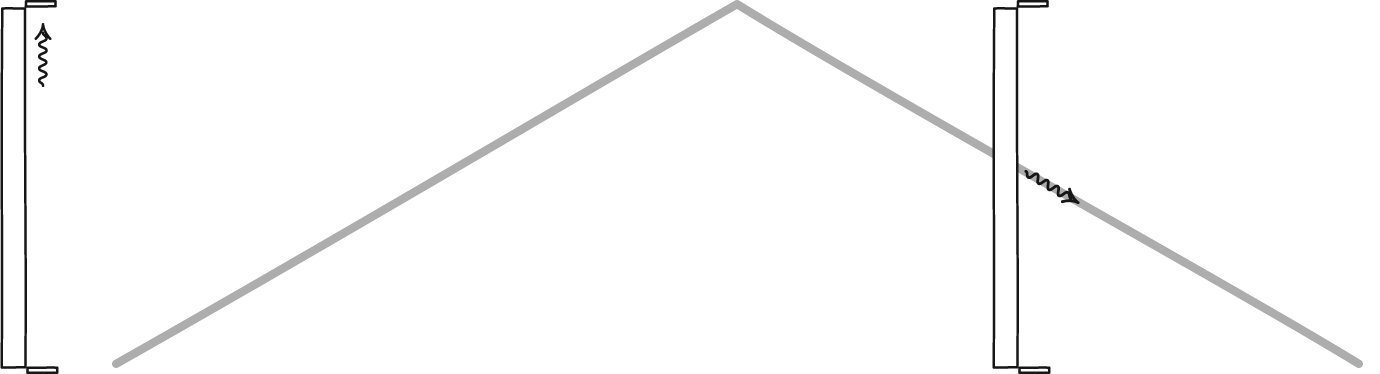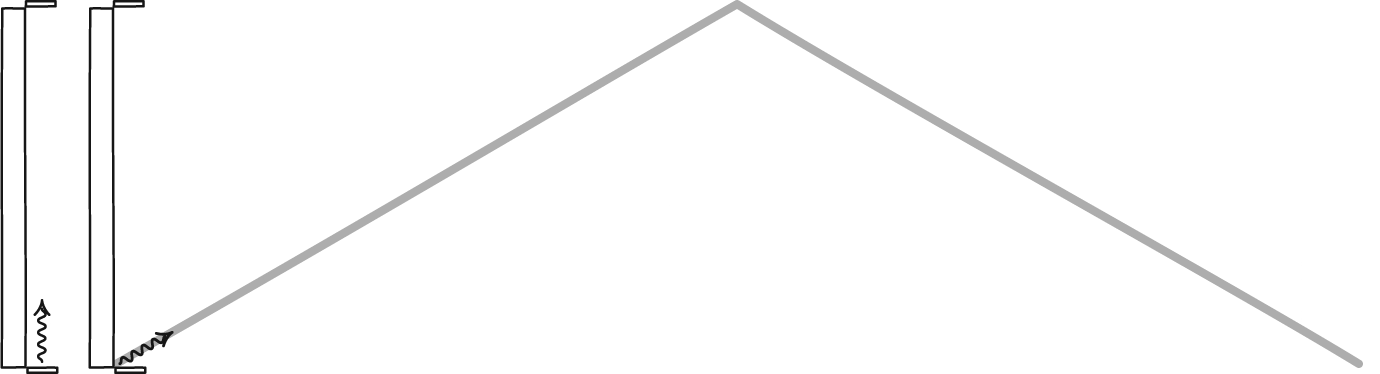
Length contraction simply means that, in the direction an object travels, all of the distances it views will appear to be compressed. The amount of that contraction is related to how close to the speed of light it’s moving. For someone at rest with respect to the fast-moving object, the object itself appears compressed. But for someone aboard the fast-moving object, whether a particle, train, or spacecraft, the cosmic distances they’re attempting to traverse will be what’s contracted.
Because the speed of light is a constant for all observers, someone moving through space (relative to the stars, galaxies, etc.) at close to the speed of light will experience time passing more slowly, as well. The best illustration is to imagine a special kind of clock: one that bounces a single photon between two mirrors. If a “second” corresponds to one round-trip journey between the mirrors, a moving object will require more time for that journey to happen. From the perspective of someone at rest, time will appear to slow down significantly for the spacecraft the closer to the speed of light they get.
With the same, constant force applied, your speed would begin to asymptote: approaching, but never quite reaching, the speed of light. But the closer to that unreachable limit you get, with every extra percentage point as you go from 99% to 99.9% to 99.999% and so on, lengths contract and time dilates even more severely.
Of course, this is a bad plan. You don’t want to be moving at 99.9999+% the speed of light when you arrive at your destination; you want to have slowed back down. So the smart plan would be to accelerate at 1g for the first half of your journey, then fire your thrusters in the opposite direction, decelerating at 1g for the second half. This way, when you reach your destination, you won’t become the ultimate cosmic bug-on-a-windshield.
Adhering to this plan, over the first part of your journey, time passes almost at the same rate as it does for someone on Earth. If you traveled to the inner Oort cloud, it would take you about a year. If you then reversed course to return home, you’d be back on Earth after about two years total. Someone on Earth would have seen more time elapse, but only by a few weeks.
But the farther you went, the more severe those differences would be. A journey to Proxima Centauri, the nearest star system to the Sun, would take about 4 years to reach, which is remarkable considering it’s 4.3 light-years away. The fact that lengths contract and time dilates means that you experience less time than the distance you’re actually traversing would indicate. Someone back home on Earth, meanwhile, would age about an extra full year over that same journey.

The brightest star in Earth’s sky today, Sirius, is located about 8.6 light-years away. If you launched yourself on a trajectory to Sirius and accelerated at that continuous 1g for the entire journey, you’d reach it in just about 5 years. Remarkably, it only takes about an extra year for you, the traveler, to reach a star that’s twice as distant as Proxima Centauri, illustrating the power of Einstein’s relativity to make the impractical accessible if you can keep on accelerating.
And if we look to larger and larger scales, it takes proportionately less additional time to traverse these great distances. The enormous Orion Nebula, located more than 1,000 light-years away, would be reached in just about 15 years from the perspective of a traveler aboard that spacecraft.
Looking even farther afield, you could reach the closest supermassive black hole — Sagittarius A* at the Milky Way’s center — in about 20 years, despite the fact that it’s ~27,000 light-years away.
And the Andromeda Galaxy, located a whopping 2.5 million light-years from Earth, could be reachable in only 30 years, assuming you continued to accelerate throughout the entire journey. Of course, someone back on Earth would experience the full 2.5 million years passing during that interval, so don’t expect to come back home.

In fact, so long as you kept adhering to this plan, you could choose any destination at all that’s presently within 18 billion light-years of us, and reach it after merely 45 years, max, had passed. (At least, from your frame of reference aboard the spacecraft!) That ~18 billion light-year figure is the limit of the reachable Universe, set by the expansion of the Universe and the effects of dark energy. Everything beyond that point is currently unreachable with our present understanding of physics, meaning that ~94% of all the galaxies in the Universe are forever beyond our cosmic horizon.
The only reason we can even see them is because light that left those galaxies long ago is just arriving today; the light that leaves them now, 13.8 billion years after the Big Bang, will never reach us. Similarly, the only light they can see from us was emitted before human beings ever evolved; the light leaving us right now will never reach them.
Still, the galaxies that are within 18 billion light-years of us today, estimated to number around 100 billion or so, are not only reachable, but reachable after just 45 years. Unfortunately, even if you brought enough fuel, a return trip would be impossible, as dark energy would drive your original location so far away that you could never return to it.
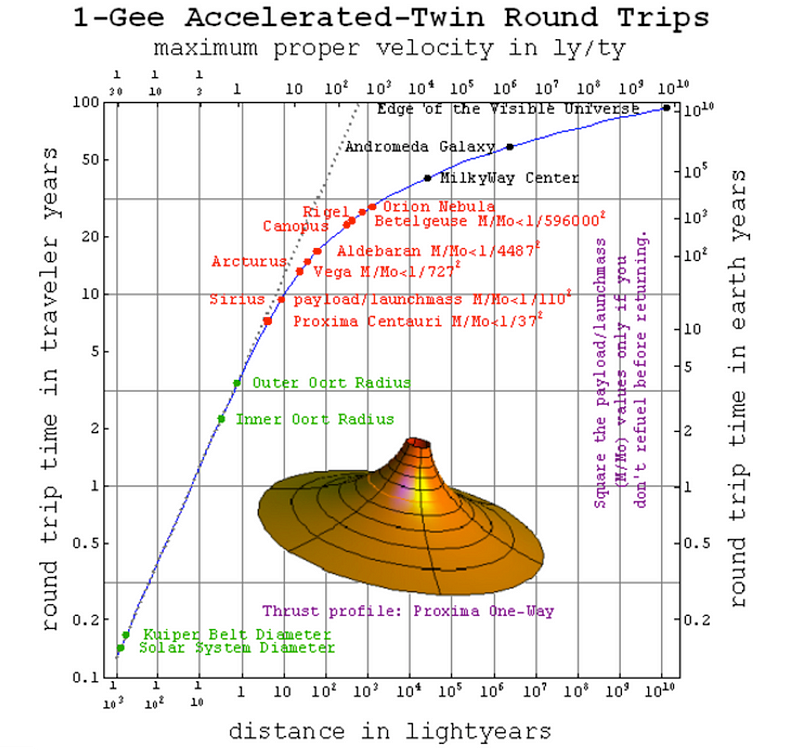
Even though we think of interstellar or intergalactic journeys as being unfeasible for human beings due to the enormous timescales involved — after all, it will take the Voyager spacecrafts nearly 100,000 years to traverse the equivalent distance to Proxima Centauri — that’s only because of our present technological limitations. If we were able to create a spacecraft capable of a constant, sustained acceleration of 1g for about 45 years, we could have our pick of where we’d choose to go from 100 billion galaxies within 18 billion light-years of us.
The only downside is that you’ll never be able to go home again. The fact that time dilates and lengths contract are the physical phenomena that enable us to travel those great distances, but only for those of us who get aboard that spacecraft. Here on Earth, time will continue to pass as normal; it will take millions or even billions of years from our perspective before that spacecraft arrives at its destination. If we never ran out of thrust, we could hypothetically reach anywhere in the Universe that a photon emitted today could reach. Just beware that if you were to go far enough, by the time you came home, humanity, life on Earth, and even the Sun will all have died out. In the end, though, the journey truly is the most important part of the story.
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





