Happy Perfect Number Day
Forget Pi day and Tau day. Make June 28th the best math holiday you’ve never considered!
“If everything was perfect, you would never learn and you would never grow.” –Beyoncé
Those of you who are math fans might celebrate either March 14th (3/14) or July 22nd (22/7) as Pi Day, depending on your month/date conventions. Perhaps you’ve joined with Bob Palais and Vi Hart as a fan of Tau Day, celebrating today, June 28th (6/28) as Tau Day in celebration of the fact that τ = 2π.

But these celebrations are only approximate, as whole number (calendar-based) celebrations of transcendental numbers must always be. But the calendar numbers of today — 6 and 28 — have some very special properties that are worthy of a celebration.
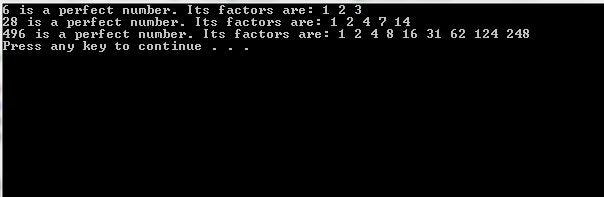
You see, unlike any other numbers displayed on your calendar (unless you were born in the year 496) numbers like 6 and 28 are perfect. So what makes a number perfect? All you have to do is positively factor it.
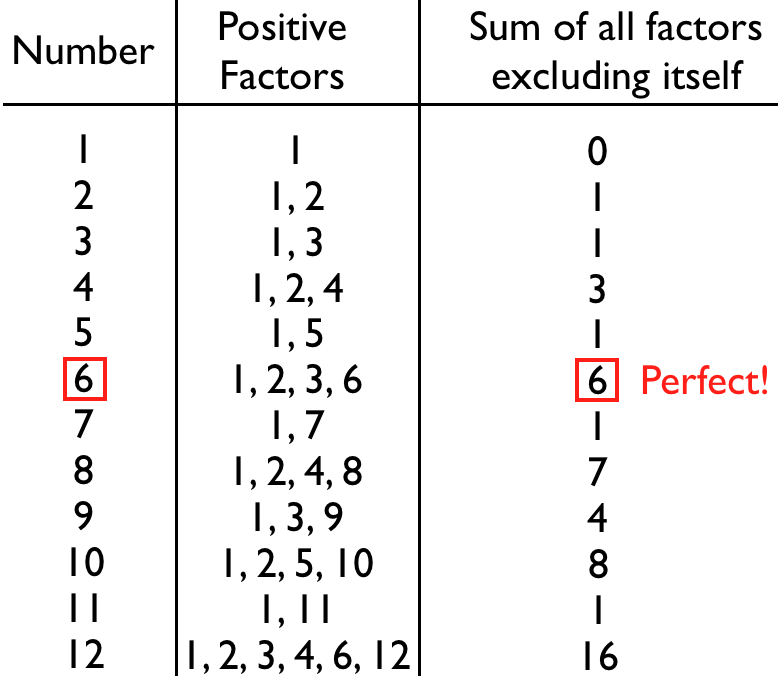
A positive factor (or a divisor), you may remember, is any number that, if you divide the original number by it, gives you a positive integer. If you add up all the positive factors of any number not including itself, you’ll get a number that’s either smaller than, greater than, or exactly equal to the original number.
If you add up all the factors excluding itself and get a number that’s less than the original one you started with, we call that number deficient. All prime numbers are maximally deficient, since its only factors are 1 and itself, and all powers of two (4, 8, 16, 32, etc.) are minimally deficient, with their sums falling just 1 shy of being perfect.
On the other hand, you might add up all the factors of a number excluding itself and get a number that’s greater than the original number; those numbers are abundant. You might look at the table above and think abundant numbers are rare, but 18, 20, 24, 30, 36 and many more are abundant; they’re quite common as you start looking at larger and larger numbers.
But perfect numbers — what Euclid called “τέλειος ἀριθμός” — are rare! For over a thousand years, only four were known.

You might look at these numbers, the ones that happen to be perfect, and start to notice a pattern here as to how these numbers can be broken down.
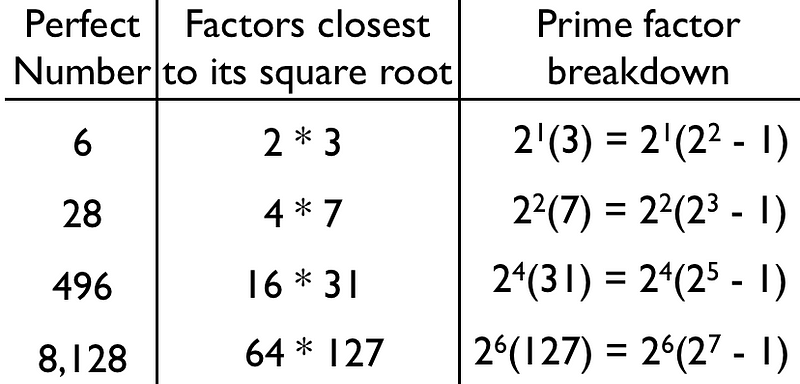
Do you remember how we talked about all powers of two — numbers like 2, 4, 8, 16, 32, etc. — being minimally deficient, where they were all just 1 shy of being perfect numbers, and how prime numbers were maximally deficient, where their only factors were 1 and themselves?
Well, as you can see, if you multiply a certain minimally deficient number by a certain maximally deficient number, you can get a perfect number out of it. But what’s more, if you look at the “prime factor breakdown” of perfect numbers, it looks like there’s a pattern for generating them! In fact, you might guess that the pattern goes something like this:
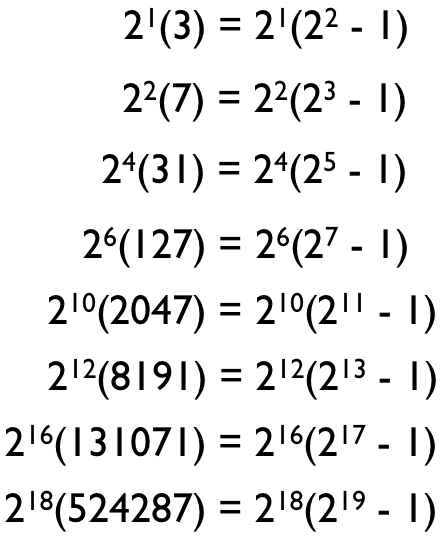
After all, the first four prime numbers are 2, 3, 5 and 7, so you might think if we simply plugged prime numbers into this formula we stumbled into at the right — where n is a prime number and the formula is 2^(n-1) * (2^n – 1) — we’d start generating perfect numbers. And you might think that this works for all primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, and so on.
As it turns out, this is a great way to generate candidate perfect numbers, but not necessarily perfect numbers themselves. In fact, all known perfect numbers do follow this formula, where n is a prime number and “2^(n-1) * (2^n – 1)” gives you a perfect number. But it isn’t true that all prime numbers generate a perfect number; it only works for a select few!
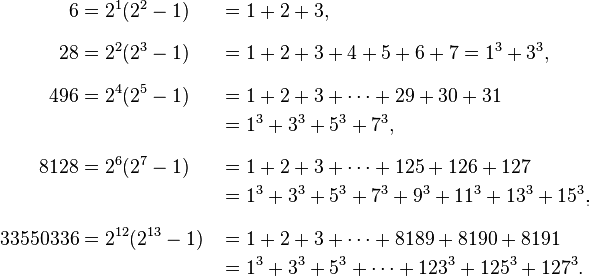
The one you might think ought to have been the 5th perfect number — 2096128, which is 2^10 * (2^11 – 1) — is actually an abundant number, and the reason is because that part in parentheses, 2^11 – 1 (which is 2047), isn’t itself prime!
2047 can be factored: 23 * 89, and therefore it isn’t prime. Because of this, the number 2096128, or 2^10 * (2^11 – 1), isn’t a perfect number, either! It’s isn’t enough to take your formula, 2^n * (2^n – 1), for n being just a regular prime number; you need to ensure that the (2^n – 1) in your formula gives you a prime number as well. This type of prime — where n is prime and (2^n – 1) is also prime — is called a Mersenne prime after the monk who studied them hundreds of years ago, and there are only 48 of them known in all existence. And they rise in size very quickly!
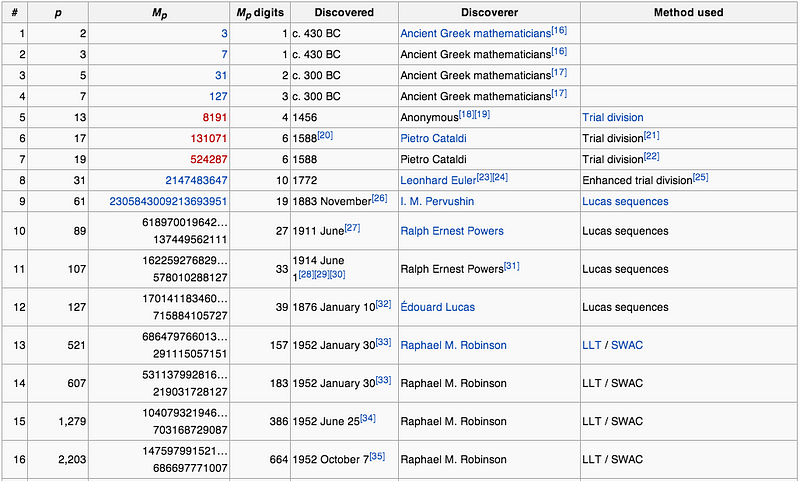
The largest of the 48 Mersenne primes is, at present, 2^57,885,161 – 1, which has over 17 million digits in it written out! I say at present because although the first 42 Mersenne primes have been verified to be in order, there are large untested gaps of candidate Mersenne primes out there. The perfect number that this corresponds to contains a whopping 34,850,339 digits, and would take about 12,000 printed pages to display.
There is also, believe it or not, a search that the computer-savvy among you can participate in: the Great Internet Mersenne Prime Search, including cash prizes for finding new ones!
If you wanted a little conjecture as to how to break the current record, here’s a fun piece of information you may want to consider. In addition to the numbers 3, 7, and 127 (the 1st, 2nd and 4th Mersenne primes), the number 170,141,183,460,469,231,731,687,303,715,884,105,727 is a Mersenne prime as well (the 12th), with 38 digits in it. That means that in addition to 6, 28, and 8,128, the following number is absolutely perfect as well: 14,474,011,154,664,524,427,946,373,126,085,988,481,573,677,491,474,835,889,066,354,349,131,199,152,128.
The crazy thing is, I think it’s very likely that the quantity (2^170,141,183,460,469,231,731,687,303,715,884,105,727 – 1) is a Mersenne prime, too, and would be one containing — are you ready — over 10^37 digits! Why do I believe that? Because of a little pattern, first noticed centuries ago:

The first four numbers that follow this pattern are definitely Mersenne primes, but is the fifth? And more over, is this a valid way to generate an infinite number of Mersenne primes? [This pattern may not necessarily hold up; there are many examples of Mersenne primes n — such as 8191, 131071, and 524287 — where 2^n – 1 (e.g., 2^8191- 1) is not a Mersenne prime itself!]
The discovery of the first billion digit Mersenne prime — that is a Mersenne prime with only 10^9 (or more) digits — will net you a cool quarter-of-a-million dollars, but only if you can verify it! A more conceivable test, although it will only get you to around 6 × 10^8 digits (and a less lucrative prize of $150,000), would be to test whether (2^2,147,483,647 – 1) is a Mersenne prime. You can have that guess from me for free; good luck!
Many candidate Mersenne primes have been shot down by showing they can be factored, usually into two primes. Just as 2047 = 23 * 89, many other candidate Mersenne primes have been shown not to be. In 1903, it was already known that (2^67 – 1) was not a Mersenne prime, but no one knew what its factors were. Frank Nelson Cole gave a talk to the American Mathematical Society entitled “On the Factorization of Large Numbers.” On the left side of the board, he computed (2^67 – 1), which he showed equaled 147,573,952,589,676,412,927. On the right, he wrote 193,707,721 × 761,838,257,287, and spend his hour lecture saying nothing and working it out.
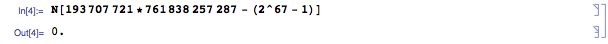
At the end, when he showed both sides were equal, he sat down to a standing ovation, allegedly the first one ever given at a mathematics talk.
The largest candidate Mersenne prime that’s been proven to be factorable so far is (2^1,168,183 – 1), which was shown (earlier this year, in February 2014) to be able to be factored into 54,763,676,838,381,762,583 (which is prime) and a 351,639-digit number, which is thought to be prime as well.
It has been proven that all the even perfect numbers that exist are of the form that are generated by Mersenne primes that follow (2^n – 1), and it is conjectured (but not yet proven) that there are no odd perfect numbers; I have a feeling that accomplishing the latter (or, somehow, finding an odd perfect number) would be one of the greatest mathematical achievements of the century!
So that’s what a perfect number is, and a whole bunch of interesting math behind it. Whether you write 6/28 or 28/6, I hope you enjoy this as perfect number day for all the June 28ths from here on out, as these rare numbers may yet have even more to teach us about the search for truth and beauty that goes beyond the limitations of our physical Universe!
Leave your comments at the Starts With A Bang forum on Scienceblogs!





