Fine-Tuning Really Is A Problem In Physics
When the Universe gives us clues, we ignore them at our own peril.
When you approach the world scientifically, you seek to gain knowledge about how it works by asking it questions about itself. You observe its behavior; you perform experiments on it; you measure specific quantities that you’re interested in. If you ask the right questions in the right ways, you can begin to gain information about what physical phenomena govern the behavior that was revealed in each and every one of your investigations.
Most of the time, your results will teach you something specific about the Universe. But every once in a while, you’ll find something that seems too good to be true. You’ll measure something that will confuse you in one of two ways: either two things that appear unrelated are perfectly (or almost perfectly) identical, or two things that appear related are extraordinarily different. This is known as fine-tuning, and it really is a problem in physics.
You don’t even need to look at physics to understand why this would be the case. Imagine, instead, you were looking at the net worths of some of the richest people in the world, as based on the Forbes Billionaires list. If you were to pick two of them at random, what would you expect to find? Sure, you’d expect that each one would be worth at least one billion dollars, but you’d also expect there would be a large difference between these two values.
If the first billionaire is worth an amount A, and the second is worth an amount B, then the difference between them is C, where A — B = C. Without any further knowledge, you should be able to assume something about C: it shouldn’t be much smaller than either A or B. In other words, if A and B are both in the billions of dollars, then it’s likely that C will be in (or close to) a value of billions as well.
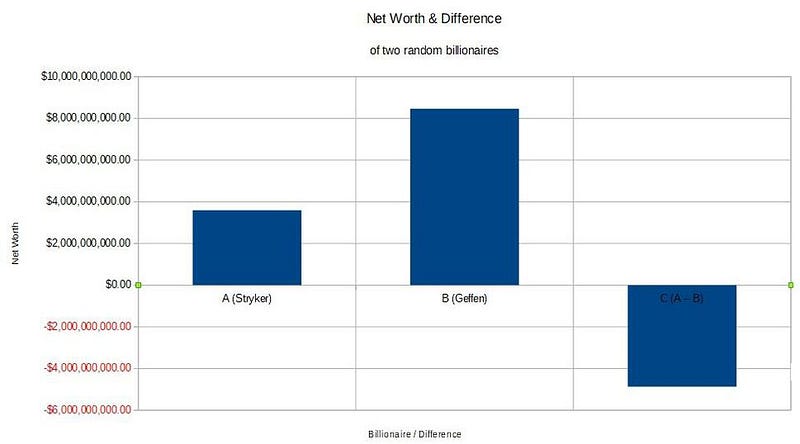
For example, A might be Pat Stryker (#703 on the list), worth, let’s say, $3,592,327,960. And B might be David Geffen (#190), worth $8,467,103,235. The difference between them, or A — B, is then -$4,874,775,275. C has a 50/50 shot of being positive or negative, but in most cases, it’s going to be of the same order of magnitude (within a factor of 10 or so) of both A and B.
But it won’t always be. For example, most of the over 2,200 billionaires in the world are worth less than $2 billion, and there are hundreds worth between $1 billion and $1.2 billion. If you happened to pick two of them at random, it wouldn’t surprise you terribly if the difference in their net worth was only a few tens of millions of dollars.

It might, however, surprise you if the difference between them was only a few thousand dollars, or was zero. “How unlikely,” you’d think. But it might not be all that unlikely after all.
After all, you don’t know which billionaires were on your list. Would you be shocked to learn the Winklevoss twins — Cameron and Tyler, the first Bitcoin billionaires — had identical net worths? Or that the Collison brothers, Patrick and John (co-founders of Stripe), had net worths that differed by only a few hundred dollars?
No, it wouldn’t be particularly surprising. In general if A is large and B is large, then A — B will also be large, unless there’s some reason for A and B to be very close together. The distribution of billionaires isn’t completely random, as there might be underlying reasons for two seemingly unrelated values to actually be related. (In the case of the net worths of the Winklevosses or the Collisons, there’s literally a blood relationship!)
In the Universe, there are many things that are finely-tuned. The expanding Universe itself is a fantastic example. At the earliest moment of the hot Big Bang, the fabric of space itself was expanding at a particular rate (the Hubble expansion rate) that happened to be enormous. At the same time, the Universe was filled with a tremendous amount of energy in the form of particles, antiparticles, and radiation.
The expanding Universe is basically a race between these two competing forces:
- the initial expansion rate, which works to drive everything apart,
- and the gravitation of all the different forms of energy present, which works to pull everything back together,
with the Big Bang serving as the starting gun. Interestingly enough, in order to wind up with the Universe we have today, these two numbers, which seem unrelated, must be finely-tuned by an incredible amount.
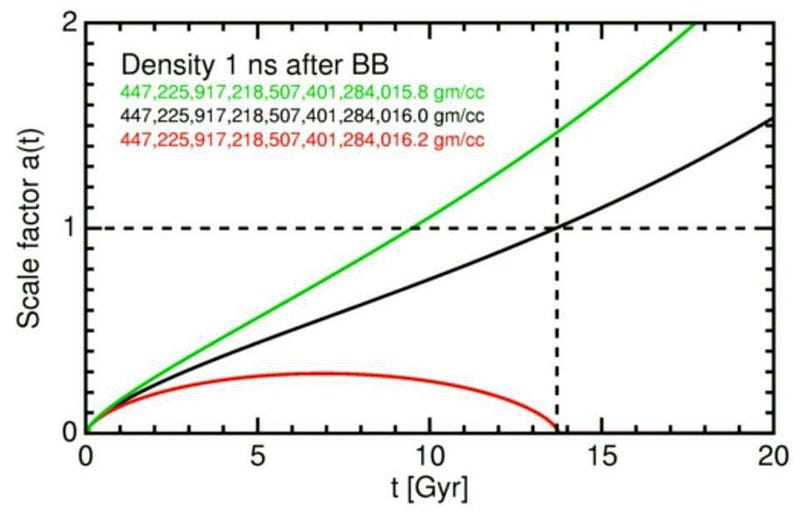
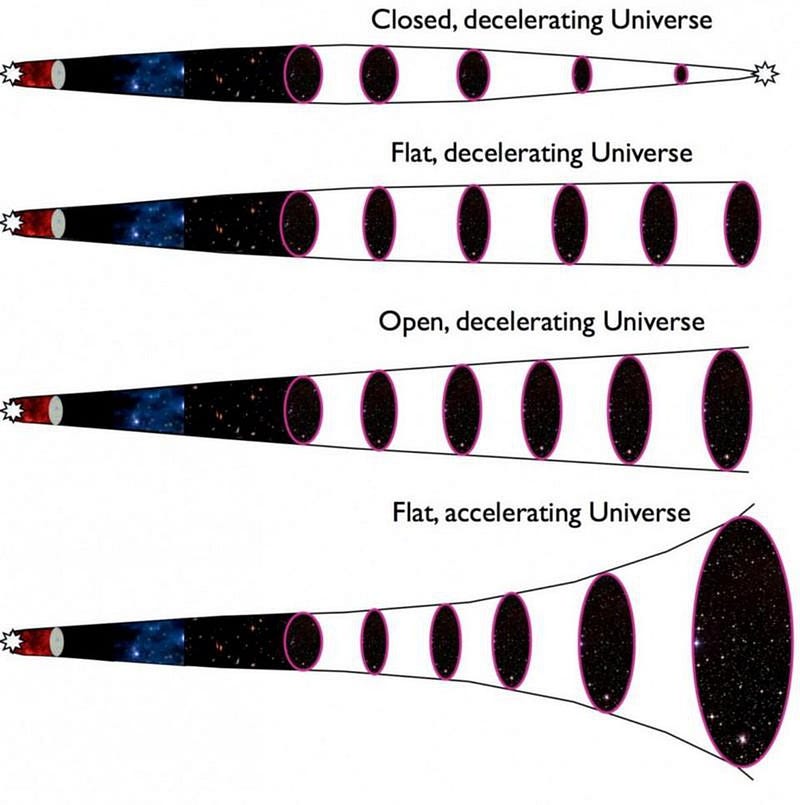
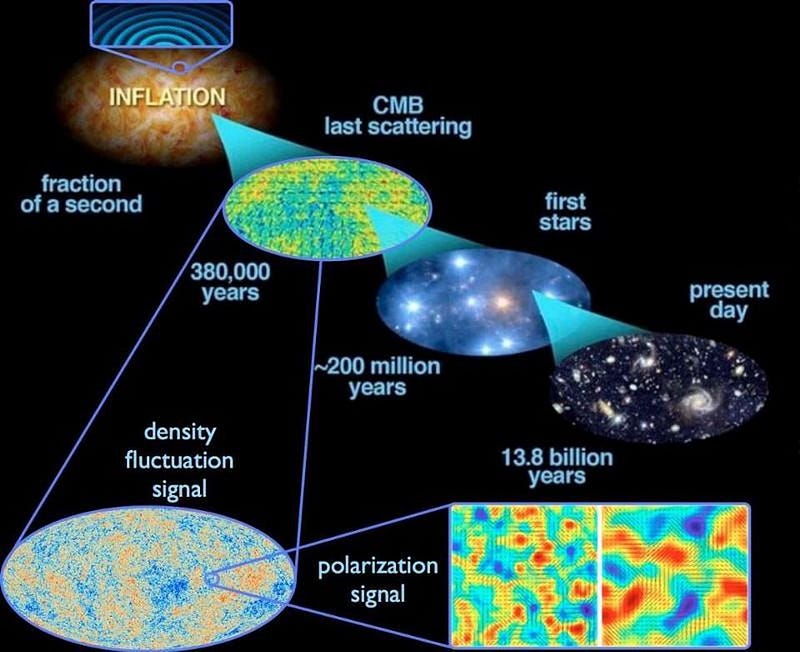
This puzzle is known as the flatness problem, as a Universe where energy and the expansion rate balance so perfectly will also be perfectly spatially flat. We can also, today, measure the curvature of the Universe by a number of different methods, such as by examining the patterns of fluctuations in the cosmic microwave background.
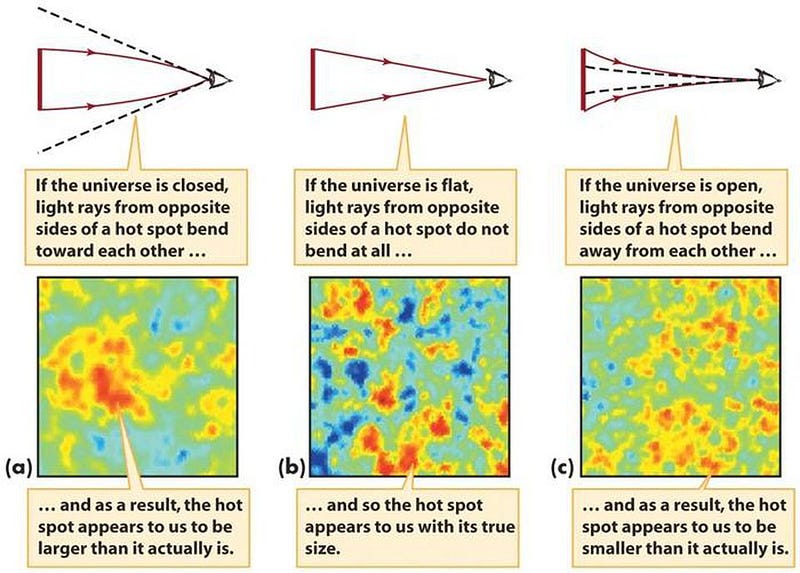
By comparing the observations we make with our theoretical predictions for what those fluctuations should look like in a Universe with varying amounts of curvature, we can determine that the Universe is extremely spatially flat, even today. If we extrapolate back to the earliest stages of the hot Big Bang based on our modern observations, we learn that the initial expansion rate and the initial energy density must be balanced to something like 50 significant digits.
When we’re faced with a puzzle like this, we have two options for how we proceed. The first is to state that this fine-tuning is simply a result of the initial conditions that are needed to give us the result we have today. After all, there are many coincidences that we observe today where two things appear closely related because they were set up, long ago, with the right conditions that would lead them to appear related today.
Venus, for example, orbits the Sun in an elliptical shape, similar to how all the planets orbit. But Venus has the smallest percent difference between its closest approach to the Sun (perihelion) and when it reaches its farthest distance from the sun (aphelion) of any of the planets.
Why is Venus more circular, and less elliptical, than any of the other planets? It’s simply due to the initial conditions of the material that gave rise to the Solar System. Neptune is the second most circular, followed by Earth. The least circular planet? Mercury, followed by Mars and then Saturn. There wasn’t a mechanism that caused these eccentricities; it had the outcome we observe today because of the (seemingly random) initial conditions our Solar System was born with.

But this is both an unappealing and an unenlightening path to take, because it assumes that there isn’t an underlying cause that gave rise to the effect we observe. The alternative option is to assume that there was some mechanism that gave rise to the apparent fine-tuning we see today.
For example, if you take a look at an enormous rock balanced precariously on a perch, you would assume that something caused it to be that way. It could be because someone carefully placed and balanced it there, or it could be because erosion and weathering happened in such a way that this structure evolved naturally. Fine-tuning doesn’t need to imply a fine-tuner, but rather that there was a physical mechanism underlying why something appears finely-tuned today. The effect may look like an unlikely coincidence, but this may not be the case if there’s a cause responsible for the effect we see.
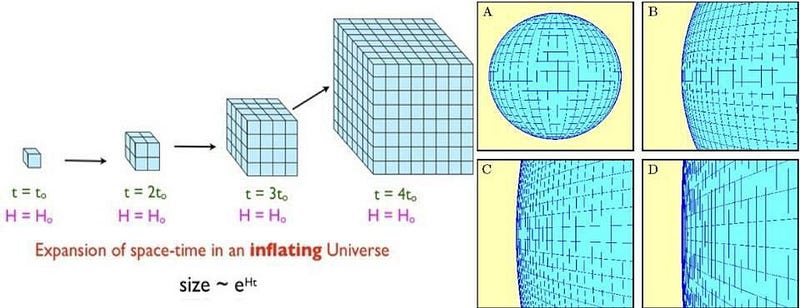
Going back to the case of the flatness problem, it’s easy to theorize some potential explanations for what would cause the Universe to appear flat today. It’s possible that the initial expansion rate and the initial energy density of the Universe arose from the same pre-existing state, causing these two value to be related and balanced.
It’s also possible that a phase of the Universe existed before the Big Bang, expanding rapidly and stretching the Universe so that it’s indistinguishable from perfectly flat. It’s possible that the Universe really is curved, but that it’s curved on a much larger scale than our observable Universe permits us to access, in the same way that you couldn’t measure the curvature of Earth solely by examining your own backyard.
The whole point of a fine-tuning argument isn’t to declare that we have a weird coincidence, and therefore anything that explains this coincidence is likely to be right. Rather, it points us to the various ways we might think about an otherwise unexplained puzzle, to try and provide a physical explanation for a phenomenon that has no obvious cause.
In science, our goal is to describe everything we observe or measure in the Universe through natural, physical explanations alone. When we see what appears to be a cosmic coincidence, we owe it to ourselves to examine every possible physical cause of that coincidence, as one of them might lead to the next great breakthrough. That doesn’t mean you should credit (or blame) a particular theory or idea without further evidence, but the possible solutions we can theorize do tell us where it might be smart to look.
As always, we have strict requirements for any such theory to be accepted, which includes reproducing all the successes of the previous leading theory, explaining these new puzzles, and also making new predictions about observable, measurable quantities that we can test. Until a new idea succeeds on all three fronts, it’s only speculation. But that speculation is still incredibly valuable. If we don’t engage in it, we’ve already given up on discovering new fundamental truths about our reality.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.





