Why Elon Musk’s Hyperloop won’t work for humans

It’s always exciting when there’s a potential new development in transportation. No one likes airports or airplanes, and let’s face it, cars and trains are slow, particularly when it comes to traversing the large distances between most major cities in countries with large land areas like the United States. The plan for a new, rapid type of transport is simple, and in theory only involves two things:

1. the ability to accelerate yourself to go fast, minimizing both friction due to moving parts as well as air resistance, and
2. the ability to counteract the gravitational pull of the Earth.

While rapid air transport and bullet trains have already been implemented in many places, their limitations and associated costs are also severe. If we could develop a new system of transportation that was low-cost, accessible, comfortable, and as fast as (or faster than) air travel, all without the gross inconveniences and high carbon-costs associated with air travel. One such proposal is Elon Musk’s Hyperloop, which aims to apply pneumatic tube technology to human-scale interstate transport. Although the physics itself isn’t a dealbreaker, applying it to the planet we have shows why it’s a both technologically-ineffective and cost-ineffective solution to our transportation problems.

This MagLev train from Japan represents one of their many Shinkansen, or bullet trains. The magnets on the track and on the train repel one another, allowing the train to levitate above the track. As electromagnets accelerate and decelerate it, the levitation effects practically eliminate the friction between moving mechanical parts, which conventional rail and road vehicles all suffer from.

If we want to consider the Hyperloop in earnest, the only responsible thing to do is to compare it with the most competitive technology with similar aims: MagLev trains. These trains work off of the principle of magnetic levitation, something that’s been well-understood and implemented on large scales for many decades now. You use powerful magnets along the track and the train to “levitate” the train above the track, both counteracting the force of gravity and removing all the friction that occurs between parts that touch each other, which is the major drawback of both roadway vehicles and conventional trains.

At the same time, you build them into an extremely aerodynamic shape and use electromagnets to accelerate and propel the train forward, and that’s how a high-speed train (or bullet train) works. But even those trains have a limit to their speed: around 270 miles-per-hour for freight trains, where the speed is still limited by a combination of air resistance and power consumption.

However, passenger trains don’t achieve the same speeds, even along the same tracks, but rather top out at about ⅔ the speed of freight trains. This isn’t because the technology can’t handle going faster; it’s because of the limitations of our bodies.

This image shows the MagLev train CRH380AL EMU at Shanghai’s Hongqiao Station. One of the fastest trains in the world, its top speeds are only suitable for passengers on long, straight sections of track. Where the track curves more steeply or severely, slower speeds are required to prevent ill effects for the passengers.

If you’ve ever been on a roller-coaster that left you nauseated, ridden in a turbulent airplane, or even been a passenger in a car that’s taken a tight turn at too high a speed, you’ll understand those limitations immediately. As long as you move at a constant speed in a straight line, smoothly and with only minimal acceleration, you can go arbitrarily fast and not suffer any ill effects. But accelerations are particularly jarring, with side-to-side and up-and-down accelerations being particularly egregious sensations for human beings. If you want to minimize the nausea factor, and actually make these high-speed trips comfortable for people to take, you have to take those limitations into account.

With that in mind, let’s turn our attention towards the Hyperloop.

The brain-child of Elon Musk, the Hyperloop aims to improve upon the principle of MagLev trains. Rather than an electrified, magnetized rail, the Hyperloop will be built inside a giant tube, and that tube will be almost completely evacuated of its air. We won’t be limited by air resistance any longer, since we’re creating a pretty good vacuum inside the tube, and so can go much faster than a MagLev train.

This 3D model of a hyperloop car/pod, designed to transport people, relies on a chamber evacuated of air and a rear propulsion device. Although this could in principle achieve remarkable speeds, understanding the constraints on what a human can comfortably withstand is of paramount importance.

Many people approach the Hyperloop with a set of unfounded worries that physics actually has no problem with.

You might worry that you won’t be able to levitate the vehicle inside, but magnetism wasn’t the only method possible. We can use the same principle as a hovercraft or an air hockey table, and have the vehicle shoot a column of air out from beneath it, enough to create a gap between it and the tube (and to keep it aloft), but not enough air to provide resistance and slow the vehicle down. It sounds like a fine line to walk, but this is actually the easy part: the laws of physics tell you that this is honestly good-to-go with current technology.

You might worry about your ability to propel the levitated craft forward at the desired speeds, but that’s easy to take care of as well. Using the same technology as a coil-gun or railgun, you can propel yourself forward in a similar fashion to a MagLev train. With no air inside, it’s not a stretch that you’d be able to reach speeds of around 800 miles-per-hour (1,300 km/hr), or a speed much faster than any currently-flying commercial aircraft. At least, for a perfectly straight track.

This variant of a Hyperloop capsule design, known as ‘Hyperloop Cheetah,’ has the technical capabilities to exceed the maximum speed ever achieved by MagLev trains due to the evacuated, practically air-free chamber it’s designed to travel through. That part of the technology is expensive but not prohibitive, but there are speed constraints that go far beyond what technological capabilities allow for.

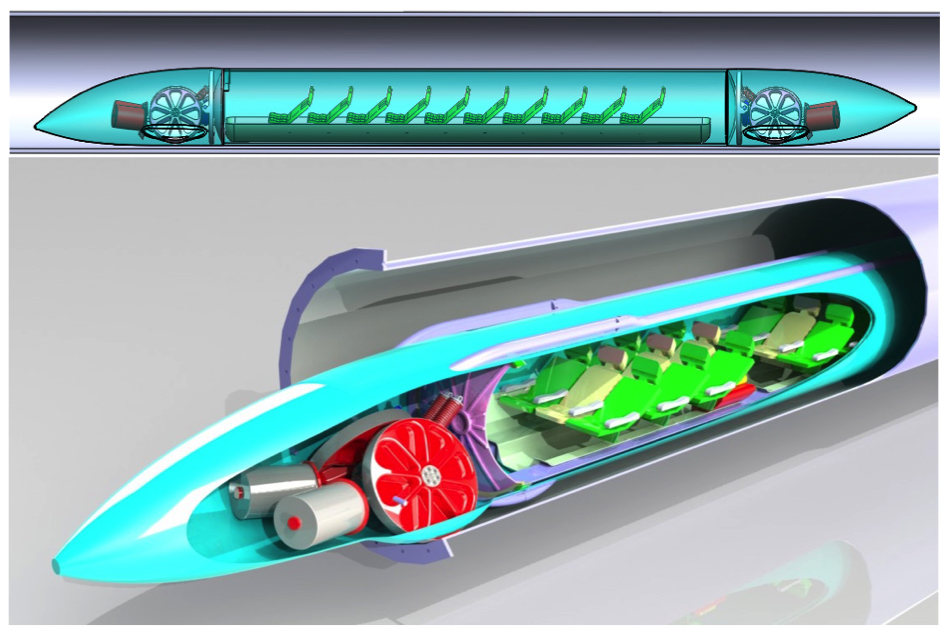
That’s right: according to the laws of physics and given the development of modern technology, there’s no problem at all in saying, “Let’s build a long, straight track for a hyperloop tube across whatever path we like.” As it was originally proposed, the first Hyperloop to be constructed would run between San Francisco and Los Angeles.

The technical obstacles that are often discussed are things like:

• How do we build a tube for a Hyperloop stably over both land and water?
• How do we make the tube and its supports stable, over the long-term, against earthquakes and the continental motions associated with the San Andreas fault?
• And how do we, even with a five-mile spacing between cars, ensure that a single car within the Hyperloop can be brought to rest from top speed within the required four-second time interval?

But these aren’t the big problems. The biggest problem associated with the Hyperloop isn’t with these engineering concerns, but rather with the very human concern of how a living being will handle the vertical and lateral accelerations that necessarily come along with such a high-speed trip.

Whenever you have a curve in your track, the radius of curvature sets the maximum safe speed for travel, and that speed is greater for freight than it is for humans, who are more sensitive to large accelerations. Any accelerations greater than about 2 m/s^2 in the lateral or vertical directions poses a difficulty for humans, placing severe restrictions on the suitability of a system like the Hyperloop for high-speed long-distance transport.

The forward-and-backwards accelerations can be controlled pretty well. But what about the fact that the terrain, the very surface of the Earth itself, isn’t flat?

This isn’t related to the fact that the Earth is spheroidal in shape, as the curvature of our surface is very small compared to the imperfections in Earth’s terrain. We have mountains, hills, valleys, rivers, and all sorts of other geological features on Earth’s surface, and we only have three ways to typically deal with them.

• In the case of a valley, water feature, or other temporary drop in elevation, we build bridges: long, supportive, elevated structures that allow for relatively straight travel across those obstacles.
• In the case of hills or mountains, we can build tunnels or otherwise blast through them, creating a relatively straight path through such obstacles.
• Or, as we most commonly do with road and rails today, we can simply curve the track, going around the largest features and rolling along with the terrain where we can.

This is where the biggest problem with the Hyperloop arises: it’s a catch-22 situation. If you want to go fast, you have to build your track incredibly straight: so straight that any curve is very slight over very large distances, which requires building stable and well-constructed elevated and/or tunnel-like structures over very long distances. On the other hand, if you want to build something cheaply, and use the surface of the Earth to support your track, you have to slow your speed to accommodate the actual terrain present on Earth.

The main problem with a high-speed system that’s reliant on traversing Earth’s surface is that the surface is not particularly free of changes in elevation or uneven terrain. The tube or track for a high-speed system, to compensate, must be made incredibly straight, and that means a mix of tunneling through large sections of Earth and supporting elevated tracks over long stretches. These factors would make construction costs prohibitive.

Infrastructure over large distances, particularly the more complex and the better-engineered it needs to be, gets progressively more and more expensive. In the case of the Hyperloop, it can not be built to only the same tolerances as say, the federal interstate system, but must have slower, more gradual turns by approximately a factor of ~50. In fact, the Hyperloop, as originally proposed, allowed for accelerations that were a factor of 7 greater than the maximum accelerations permissible for the passenger-carrying bullet train system in Japan: the Shinkansen.

If you’ve ever been on a poorly designed roller coaster and left the ride with your stomach in a knot, it’s because you’re moving too quickly through a curve, either horizontally or vertically. The constraints we normally apply to the accelerations a human can comfortably experience are measured in g-forces, or accelerations relative to the acceleration caused by Earth’s gravity at the surface.

Humans can only handle accelerations of ~2 m/s² (about ⅕th the acceleration of gravity) in either the vertical or lateral directions without inducing nausea, particularly over long periods of time. Roller coasters exceed this, but usually only for seconds at a time.

Roller coasters are notorious for causing large lateral and vertical accelerations to their human riders at relatively high speeds, but only for short periods of time. There are severe constraints on what a human can endure, in terms of accelerations, without experiencing severe discomfort, nausea, and vomiting; above that threshold, the loss of consciousness becomes a risk.

It would take a living being with superhuman tolerances to endure greater accelerations for many minutes at a time, and that’s precisely what the Hyperloop offers. Even at 800 miles-per-hour, a trip from Los Angeles to San Francisco would take about half an hour. If the typical g-forces experienced along that journey are more than about 0.2g, and the Hyperloop’s design accepts g-forces of 1-1.5g, routine nausea and vomiting should be the expected outcome.

The reason is straightforward from a physics perspective: accelerations are proportional to the vehicles speed, squared, divided by the radius-of-curvature of the path that the vehicle takes.

A good analogy is the federal interstate system, which is a relatively straight series of roads designed for vehicles to travel along them at relatively high speeds without causing discomfort to the driver and their passengers. A car that travels at 70 mph on the interstate through a carefully designed radius-of-curvature will have its passengers experience g-forces no greater than that threshold of ~0.2g, and that’s one of the two reasons that there are always speed reduction signs when you pass through a tighter-than-average curve. (The other reason is that the force of static friction between the tires and the road might be insufficient to keep your car from skidding out-of-control at higher speeds through a tight enough turn.)

Whenever a moving vehicle accelerates through a turn, changing its direction, it experiences a centripetal force. That force will also be felt by the passengers and driver, and beyond a certain threshold, will not only lead to an intense nausea sensation, but could lead to safety issues. For the case of a car on the road, if the centripetal force exceeds the frictional force between the tires and the road, control of the car will be lost.

For any system that purports to go faster, such as the Hyperloop, you have to increase the radius of curvature for the track accordingly to keep the g-forces down. If you propose your Hyperloop to travel at 500 mph – about 7.1 times a typical interstate speed – the radius of curvature of the track must be straighter by a factor of 50, or about (7.1)², than an interstate. To increase the speed to 700 mph, or ten times the normal interstate speed, the track must now be a factor of 100 (which is 10²) straighter than the interstate system is. And to reach the design specification of 800 mph, the track must be a factor of 130 straighter than the present interstate system.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

And that’s where the Hyperloop’s true problems lie.

When you apply the required “straightness” conditions in both the horizontal and vertical directions to the construction of the Hyperloop, you run into the biggest problem of all: it is not possible to build your Hyperloop along the surface of the Earth between most cities. The Earth’s surface, all across the United States (like most locations on Earth), is simply not straight enough for it. You’ll need to either sacrifice speed — defeating the purpose of the Hyperloop entirely, where a conventional bullet/MagLev train would easily match it — or you’ll need to build a track that is alternately elevated above the Earth’s surface and then tunnels through numerous geographic features. If we choose the latter option, we’re looking at costs that aren’t in the tens of billions of dollars, like it would be for a run-of-the-mill high speed rail project, but instead would quickly escalate into the multiple trillions of dollars.

Because most of the terrain between major cities has numerous elevation changes and uneven terrain, there will be a maximum radius-of-curvature to any section of track for a Hyperloop. The greater the curvature, the slower one must move and still have the journey be safe for humans.

All of this, of course, only accounts for the initial, up-front construction costs. Even if we were to make that investment, we’d still only get a very fragile system whose maintenance and safety costs have not even been quantified yet. Although there may yet be a few very flat, seismically stable areas of the Earth where a Hyperloop system would make sense, it’s a very poor choice of infrastructure between most of our major cities. If you’re on either of the coasts or you have to go through one of numerous mountain ranges — the Rockies, the Cascades, the Appalachians, etc. — the combination of high construction costs and the difficulty in carving a path that’s safe for humans at high speeds makes the Hyperloop completely ill-suited as a vehicle for transporting humans.

These concerns must be addressed with solid plans, not just mere hand-waving. Unless passengers suddenly become eager and willing to endure long periods of intense nausea and vomiting, the constraints of our actual, physical reality will prevent the Hyperloop, as proposed, from ever becoming a reality.