Does the climax of the movie ‘Gravity’ violate simple physics?

Should George Clooney’s character have floated away? Or do the laws of physics tell a different story?
“You’ve got to learn to let go.” –Matt Kowalski, Gravity
The movies play an incredibly important role in firing our imaginations about what’s possible for humanity’s future, and nowhere is that more apparent than in the realm of space travel. Over the past couple of years, movies like Interstellar, The Martian and Gravity have helped us dream up what’s possible for the future, yet they also leave us with questions about how accurate they might be. Inspired by this, I received a question from Troy Stuart, who wants to know:
The wife and I are watching Gravity tonight when this comes up. [See picture, below.] My question is at the point when the tether is stretched tight and they are hanging out in space, why when George releases does he drift away? Weight is at that point equal and is not an issue. The wife thinks because of the mass is different they float in space at different speeds. I’m saying the mass is only an issue when a change in direction is trying to be achieved. So… why does George float away when he unhooked himself?
Here’s the picture in question.

The scene is that the two astronauts are passing by the International Space Station, desperate to get to it. One of the Soyuz modules is still there, with its parachute deployed. Ryan Stone (Sandra Bullock) and Matt Kowalski (George Clooney) try and grab on; both fail, but Stone gets her leg tangled in the parachute cord and grabs onto Kowalski. The cords won’t support them both, they begin to see, and so Kowalski detaches himself and slowly drifts away into space, away from Stone and the space station.
But there’s a problem with this scenario, as Troy rightly points out. And the problem is just as simple as this: it seems to contradict Newton’s 1st law of motion.

Newton’s 1st law is perhaps the oldest law of physics known to humanity: the fact that objects at rest stay at rest, and objects in motion stay in constant motion, unless acted on by an outside force. Once Stone and Kowalski are attached to the parachute cord — once the cord goes taut and doesn’t stretch or move any longer — they should all be moving at the same speed and in the same direction. On the surface, it seems that there’s simply no reason that there should even be any tension in the parachute cord, since if they’re all experiencing the same constant motion, there’s no acceleration, and hence there’s no force. And yet, when Kowalski is released, he drifts away all the same.

The thing is, there are outside, external forces. There’s the force of gravity from the Earth, for example. There’s a very slight — but non-negligible — drag force from the very tenuous atmosphere at those high altitudes. (This is why satellites in low-Earth orbit need “boosts” every once in a while, or they de-orbit and burn up in the atmosphere.) The International Space Station is certainly far more massive than either Stone or Kowalski, and hence it experiences a greater gravitational force. But that shouldn’t matter, because Newton’s third law, the one that tells us that F = ma, tells us that the acceleration of the ISS, of Stone and of Kowalski should all be the same, even though their masses are different.
The drag force is interesting, since that’s dependent on an object’s density, its surface area, and its physical size. It’s the reason why, if Galileo really did perform his “drop two balls of different mass but the same composition” experiment off the leaning tower of Pisa, he’d have found that the heavier ball hit the ground first: compared to a 10 lb. lead weight, a 1 lb. lead weight would experience only 10% the force of gravity, but 22% the drag force! A lighter, less dense object — like a person — would experience a larger relative drag force than the ISS, and hence would slow down a little more easily in an orbit.

But not by enough to cause the effect that they show in Gravity! The density of air at ISS altitudes is so sparse that it would take months for Kowalski to drift away. In fact, a simple “tug” might propel him towards the spacecraft, rendering the whole tether scene moot.
But there’s something that — if you take the movie poster as gospel — we haven’t been considering. What if, instead of looking at the tether as a purely linear system, we take note of the fact that there are angles here?

Take a look at that: Kowalski is clearly at an angle to Stone, who clearly is at an angle to the ISS. What would cause that to happen in space? If the entire spacecraft is rotating! Even if it’s just a little bit, which would happen if a launch or collision took place prior (as it does in the movie) in any location other than the perfect center-of-mass of the ISS. If you’ve ever swung a ball around on a string and then “snapped” the string, you know that the ball flies off in a straight line.
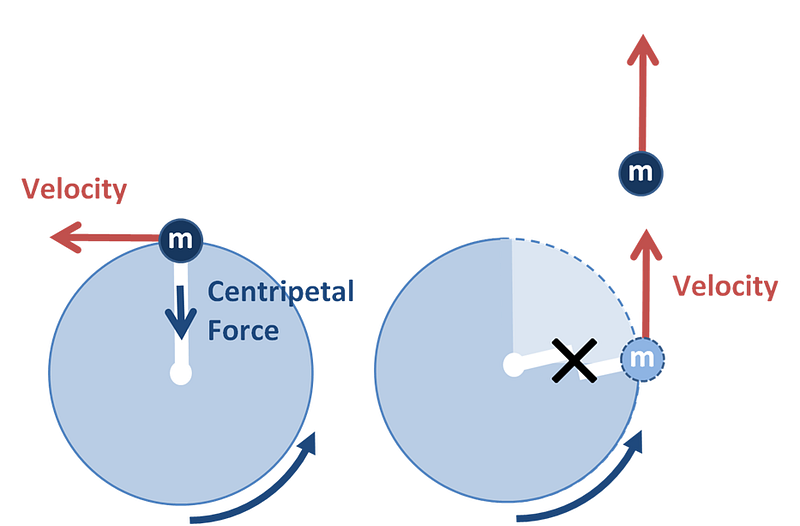
In space, that rotation could be incredibly slow; so slow that it’s barely perceptible in an extended camera shot. But it would be sufficient to do all of the following:
- Keep the tether taut.
- Provide a risk of a more massive weight at the end breaking the tether.
- And, if the weight were to become detached (e.g., Kowalski lets go), it would move off from its own inertia, away from the tethered masses.
So Troy, you’re right, there does need to be some form of acceleration in order to cause the tether to be taut, for the mass of the people to risk breaking the parachute cord and for Kowalski, when he lets go, to actually move away. This acceleration could be caused either by an external force, which leads to a change in your speed, or by a rotational motion, which leads to a change in direction. Based on what we saw in the movie itself, I’m going to go with a change in direction: a very small one, but one sufficient to cause what the movie displayed.

Perhaps I don’t watch movies the way most scientists watch movies; I don’t go looking for flaws or holes or ways to claim, “that’s impossible!” I try and find a way in my head to make it work within the possibilities of the laws of physics, and I think I’ve found one here, so I’m going with it! Rotation played a big role in The Martian as well, and in fact the one time I wanted to yell at Matt Damon was when he punctured a hole in his spacesuit’s hand to “fly” towards his rescue, I couldn’t understand why he didn’t hold his hand closer to his center of mass to better control himself!
In summary, an astronaut as experienced as Kowalski should have known to give one last mighty “tug” to bring himself in, unless the rotation of the ISS was much greater than the camera angles showed, making that an impossibility. But unless there is some sort of acceleration — and rotation seems like the only option — there’s no reason he should have floated to his demise. So that’s got to be the explanation. Either that, or someone valued the plot, the story and the outcome over the science, and they just needed a non-judgmental astrophysicist to come along and give them a retconned explanation!
Have a question or suggestion for the next Ask Ethan? Ask them at startswithabang at gmail dot com!
This post first appeared at Forbes. Leave your comments on our forum, check out our first book: Beyond The Galaxy, and support our Patreon campaign!





