Dark Matter’s Biggest Problem Might Simply Be A Numerical Error

It’s one of cosmology’s biggest unsolved mysteries. The strongest argument against it may have just evaporated.

The ultimate goal of cosmology contains the greatest ambition of any scientific field: to understand the birth, growth, and evolution of the entire Universe. This includes every particle, antiparticle, and quantum of energy, how they interact, and how the fabric of spacetime evolves alongside them. In principle, if you can write down the initial conditions describing the Universe at some early time — including what it’s made of, how those contents are distributed, and what the laws of physics are — you can simulate what it will look like at any point in the future.

In practice, however, this is an enormously difficult task. Some calculations are easy to perform, and connecting our theoretical predictions to observable phenomena is clear and easy. In other instances, that connection is much harder to make. These connections provide the best observational tests of dark matter, which today makes up 27% of the visible Universe. But one test, in particular, is a test that dark matter has failed over and over. At last, scientists might have figured out why, and the entire thing might be no more than a numerical error.

On a logarithmic scale, the Universe nearby has the solar system and our Milky Way galaxy. But far beyond are all the other galaxies in the Universe, the large-scale cosmic web, and eventually the moments immediately following the Big Bang itself. Although we cannot observe farther than this cosmic horizon which is presently a distance of 46.1 billion light-years away, there will be more Universe to reveal itself to us in the future. The observable Universe contains 2 trillion galaxies today, but as time goes on, more Universe will become observable to us, perhaps revealing some cosmic truths that are obscure to us today. (WIKIPEDIA USER PABLO CARLOS BUDASSI)

When you think about the Universe as it is today, you can immediately recognize how different it appears when you examine it on a variety of length scales. On the scale of an individual star or planet, the Universe is remarkably empty, with only the occasional solid object to run into. Planet Earth, for example, is some ~10³⁰ times denser than the cosmic average. But as we go to larger scales, the Universe begins to appear much smoother.

An individual galaxy, like the Milky Way, might be only about a few thousand times denser than the cosmic average, while if we examine the Universe on the scales of large galaxy groups or clusters (spanning some ~10-to-30 million light years), the densest regions are just a few times denser than a typical region. On the largest scales of all — of a billion light-years or more, where the largest features of the cosmic web appear — the Universe’s density is the same everywhere, down to a precision of about 0.01%.

In modern cosmology, a large-scale web of dark matter and normal matter permeates the Universe. On the scales of individual galaxies and smaller, the structures formed by matter are highly non-linear, with densities that depart from the average density by enormous amounts. On very large scales, however, the density of any region of space is very close to the average density: to about 99.99% accuracy. (WESTERN WASHINGTON UNIVERSITY)

If we model our Universe in accordance with the best theoretical expectations, as supported by the full suite of observations, we expect that it began filled with matter, antimatter, radiation, neutrinos, dark matter, and a tiny bit of dark energy. It should have begun almost perfectly uniform, with overdense and underdense regions at the 1-part-in-30,000 level.

In the earliest stages, numerous interactions all happen simultaneously:

gravitational attraction works to grow the overdense regions,
particle-particle and photon-particle interactions work to scatter off of (and impart momentum to) the normal matter (but not the dark matter),
and radiation free-streams out of overdense regions that are small enough in scale, washing out structure that forms too early (on too small of a scale).

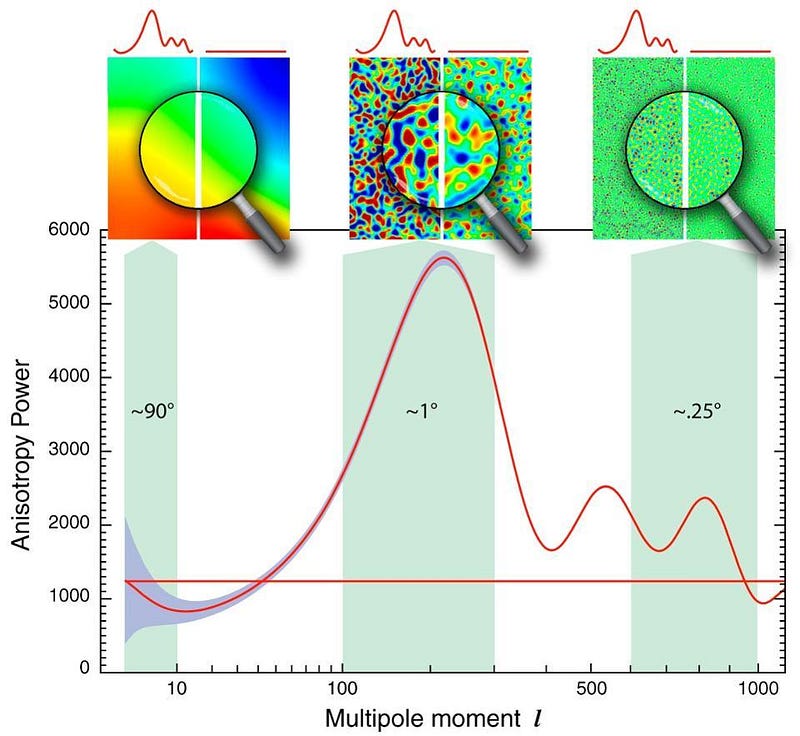
The fluctuations in the cosmic microwave background, as measured by COBE (on large scales), WMAP (on intermediate scales), and Planck (on small scales), are all consistent with not only arising from a scale-invariant set of quantum fluctuations, but of being so low in magnitude that they could not possibly have arisen from an arbitrarily hot, dense state. The horizontal line represents the initial spectrum of fluctuations (from inflation), while the wiggly one represents how gravity and radiation/matter interactions have shaped the expanding Universe in the early stages. The CMB holds some of the strongest evidence supporting both dark matter and cosmic inflation. (NASA / WMAP SCIENCE TEAM)

As a result, by the time the Universe is 380,000 years old, there’s already an intricate pattern of density and temperature fluctuations, where the largest fluctuations occur on a very specific scale: where the normal matter maximally collapses in and the radiation has minimal opportunity to free-stream out. On smaller angular scales, the fluctuations exhibit periodic peaks-and-valleys that decline in amplitude, just as you’d theoretically predict.

Because the density and temperature fluctuations — i.e., the departure of the actual densities from the average density — are still so small (much smaller than the average density itself), this is an easy prediction to make: you can do it analytically. This pattern of fluctuations should show up, observationally, in both the large-scale structure of the Universe (showing correlations and anti-correlations between galaxies) and in the temperature imperfections imprinted in the Cosmic Microwave Background.

The density fluctuations that appear in the cosmic microwave background (CMB) arise dependent on the conditions the Universe was born with as well as the matter-and-energy contents of our cosmos. These early fluctuations then provide the seeds for modern cosmic structure to form, including stars, galaxies, clusters of galaxies, filaments, and large-scale cosmic voids. The connection between the initial light from the Big Bang and the large-scale structure of galaxies and galaxy clusters we see today is some of the best evidence we have for the theoretical picture of the Universe put forth by Jim Peebles. (CHRIS BLAKE AND SAM MOORFIELD)

In physical cosmology, these are the kinds of predictions that are the easiest to make from a theoretical perspective. You can very easily calculate how a perfectly uniform Universe, with the same exact density everywhere (even if it’s mixed between normal matter, dark matter, neutrinos, radiation, dark energy, etc.), will evolve: that’s how you calculate how your background spacetime will evolve, dependent on what’s in it.

You can add in imperfections on top of this background, too. You can extract very accurate approximations by modeling the density at any point by the average density plus a tiny imperfection (either positive or negative) superimposed atop it. So long as the imperfections remain small compared to the average (background) density, the calculations for how these imperfections evolve remains easy. When this approximation is valid, we say that we’re in the linear regime, and these calculations can be done by human hands, without the need for a numerical simulation.

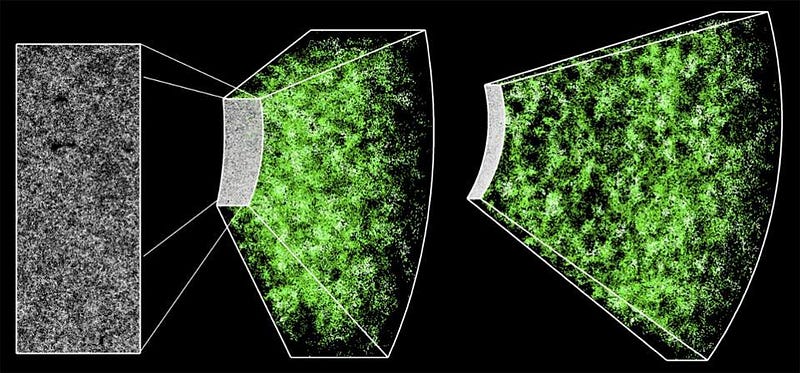
The 3D reconstruction of 120,000 galaxies and their clustering properties, inferred from their redshift and large-scale structure formation. The data from these surveys allows us to perform deep galaxy counts, and we find that the data is consistent with an expansion scenario and an almost-perfectly uniform initial Universe. However, if we looked at the Universe on smaller scales, we’d find that the departures from the average density are enormous, and we must go far into the non-linear regime to calculate (and simulate) the effective structures that form. (JEREMY TINKER AND THE SDSS-III COLLABORATION)

This approximation is valid at early times, on large cosmic scales, and where density fluctuations remain small compared to the average overall cosmic density. This means that measuring the Universe on the largest cosmic scales should be a very strong, robust test of dark matter and our model of the Universe. It should come as no surprise that the predictions of dark matter, particularly on the scales of galaxy clusters and larger, are amazingly successful.

However, on the smaller cosmic scales — particularly on the scales of individual galaxies and smaller — that approximation is no longer any good. Once the density fluctuations in the Universe become large compared to the background density, you can no longer do the calculations by hand. Instead, you need numerical simulations to help you out as you transition from the linear to the non-linear regime.

In the 1990s, the first simulations started to come out that went deep into the realm of non-linear structure formation. On cosmic scales, they enabled us to understand how structure formation would proceed on relatively small scales that would be affected by the temperature of dark matter: whether it was born moving quickly or slowly relative to the speed of light. From this information (and observations of small-scale structure, such as the absorption features by hydrogen gas clouds intercepted by quasars), we were able to determine that dark matter must be cold, not hot (and not warm), to reproduce the structures we see.

The 1990s also saw the first simulations of dark matter halos that form under the influence of gravity. The various simulations had a wide range of properties, but they all exhibited some common features, including:

a density that reaches a maximum in the center,
that falls off at a certain rate (as ρ ~ r^-1 to r^-1.5) until you reach a certain critical distance that depends on the total halo mass,
and then that “turns over” to fall off at a different, steeper rate (as ρ ~ r^-3), until it falls below the average cosmic density.

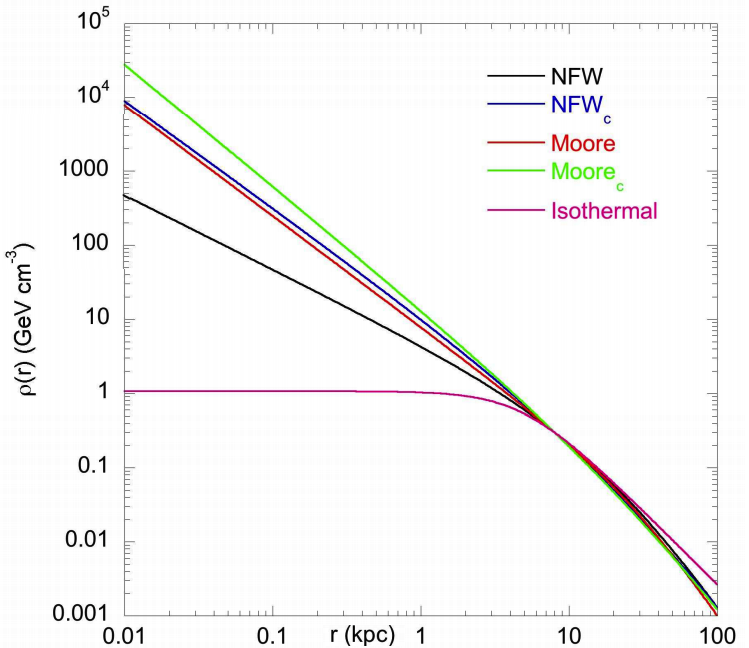
Four different dark matter density profiles from simulations, along with a (modeled) isothermal profile (in red) that better matches the observations but that simulations fail to reproduce. (R. LEHOUCQ, M. CASSÉ, J.-M. CASANDJIAN, AND I. GRENIER, A&A, 11961 (2013))

These simulations predict what are known as “cuspy halos,” because the density continues to rise in the innermost regions even beyond the turnover point, in galaxies of all sizes, including the smallest ones. However, the low-mass galaxies we observe don’t exhibit rotational motions (or velocity dispersions) that are consistent with these simulations; they are much better fit by “core-like halos,” or halos with a constant density in the innermost regions.

This problem, known as the core-cusp problem in cosmology, is one of the oldest and most controversial for dark matter. In theory, matter should fall into a gravitationally bound structure and undergo what’s known as violent relaxation, where a large number of interactions cause the heaviest-mass objects to fall towards the center (becoming more tightly bound) while the lower-mass ones get exiled to the outskirts (becoming more loosely bound) and can even get ejected entirely.

The ancient globular cluster Messier 15, a typical example of an incredibly old globular cluster. The stars inside are quite red, on average, with the bluer ones formed by the mergers of old, redder ones. This cluster is highly relaxed, meaning the heavier masses have sank to the middle while the lighter ones have been kicked into a more diffuse configuration or ejected entirely. This effect of violent relaxation is a real and important physical process, but it may not be representative of the actual physics at play in a dark matter halo. (ESA/HUBBLE & NASA)

Since similar phenomena to the expectations of violent relaxation were seen in the simulations, and all the different simulations had these features, we assumed that they were representative of real physics. However, it’s also possible that they don’t represent real physics, but rather represent a numerical artifact inherent to the simulation itself.

You can think of this the same way you think of approximating a square wave (where the value of your curve periodically switches between +1 and -1, with no in-between values) by a series of sine wave curves: an approximation known as a Fourier series. As you add progressively greater numbers of terms with ever-increasing frequencies (and progressively smaller amplitudes), the approximation gets better and better. You might be tempted to think that if you added up an infinitely large number of terms, you’d get an arbitrarily good approximation, with vanishingly small errors.

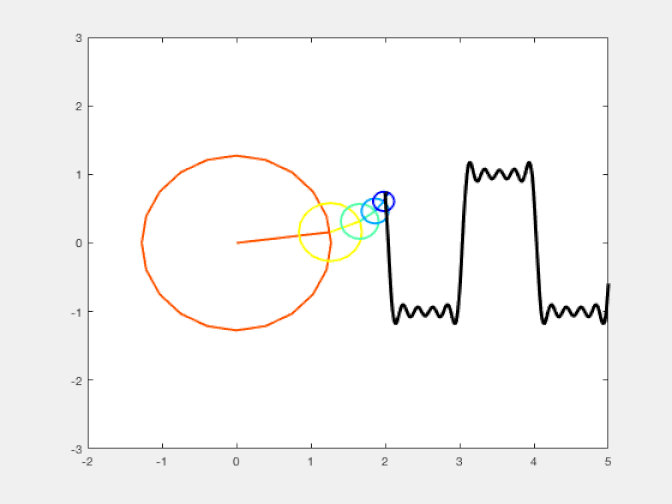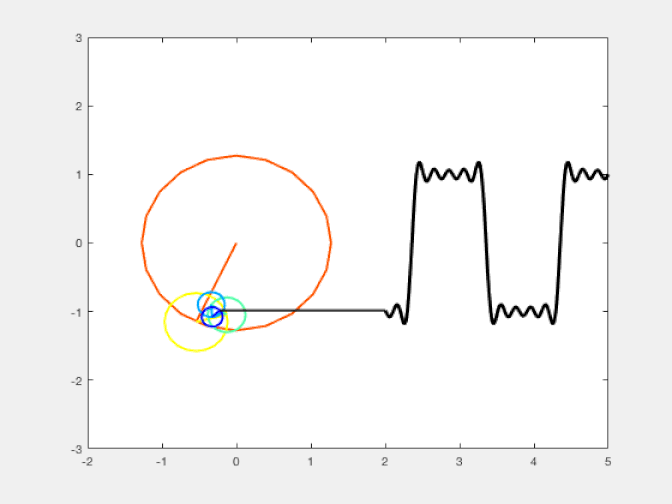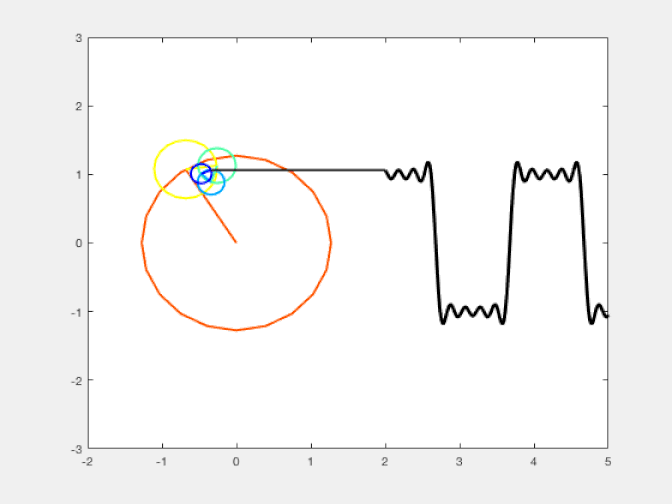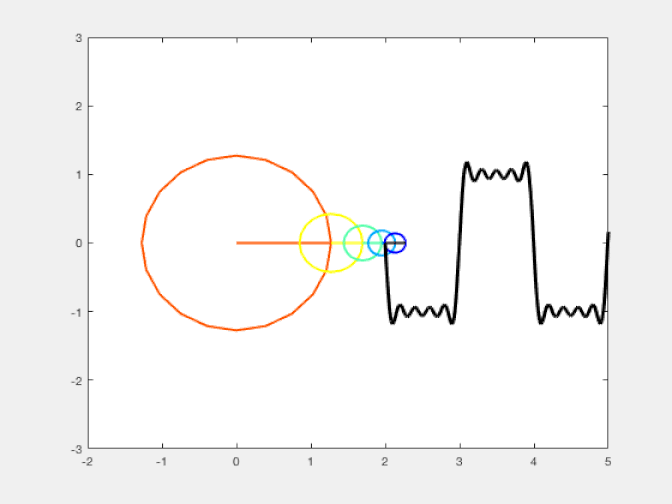
You can approximate any curve at all with an infinite series of oscillating waves (similar to one dimension of motion around circles of different sizes) with increasing frequencies to reach better and better approximations. However, no matter how many circles you use to approximate a square wave, there will always be an ‘overshoot’ of the desired value by about 18%: a numerical artifact that persists by the very nature of the calculational technique itself. (ROCKDOCTOR / IMGUR)

Only, that’s not true at all. Do you notice how, even as you add more and more terms to your Fourier series, you still see a very large overshoot anytime you transition from a value of +1 to -1 or a value of -1 to +1? No matter how many terms you add, that overshoot will always be there. Not only that, but it doesn’t asymptote to 0 as you add more and more terms, but rather to a substantial value (around 18%) that never gets any smaller. That’s a numerical effect of the technique you use, not a real effect of the actual square wave.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Remarkably, a new paper by A.N. Baushev and S.V. Pilipenko, just published in Astronomy & Astrophysics, asserts that the central cusps seen in dark matter halos are themselves numerical artifacts of how our simulations deal with many-particle systems interacting in a small volume of space. In particular, the “core” of the halo that forms does so because of the specifics of the algorithm that approximates the gravitational force, not because of the actual effects of violent relaxation.

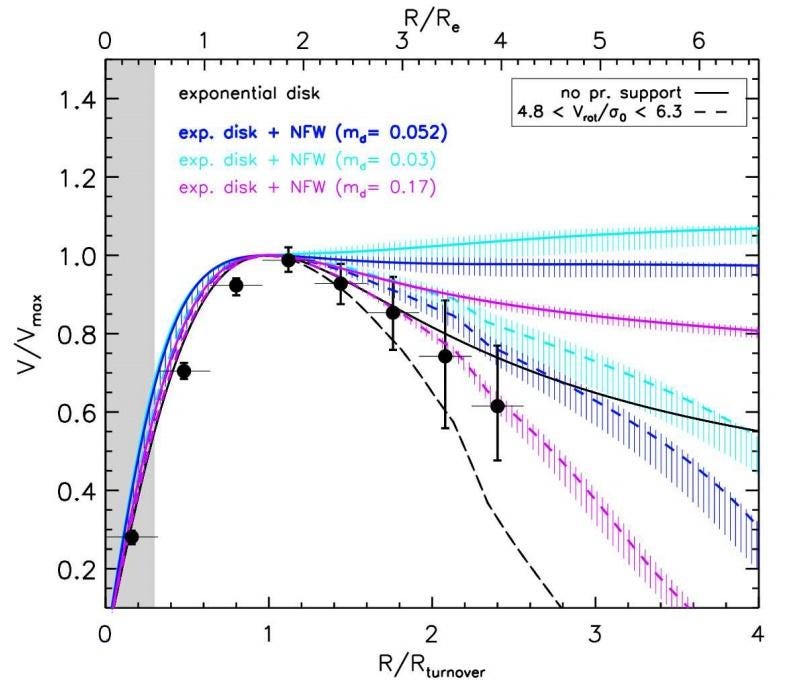
The dark matter models of today (top curves) fail to match the rotation curves, as (black curve) does the no dark matter model. However, models that allow dark matter to evolve with time, as expected, match up remarkably well. It is possible, as hinted at by recent work, that the mismatch between simulations and observations could be due to an error inherent to the simulation method used. (P. LANG ET AL., ARXIV:1703.05491, SUBMITTED TO APJ)

In other words, the dark matter densities we derive inside each halo from simulations may not actually have anything to do with the physics governing the Universe; instead, it may simply be a numerical artifact of the methods we’re using to simulate the halos themselves. As the authors themselves state,

“This result casts doubts on the universally adopted criteria of the simulation reliability in the halo center. Though we use a halo model, which is theoretically proved to be stationary and stable, a sort of numerical ’violent relaxation’ occurs. Its properties suggest that this effect is highly likely responsible for the central cusp formation in cosmological modelling of the large-scale structure, and then the ’core-cusp problem’ is no more than a technical problem of N-body simulations.” –Baushev and Pilipenko

Unsurprisingly, the only problems for dark matter in cosmology occur on cosmically small scales: far into the non-linear regime of evolution. For decades, contrarians opposed to dark matter have latched onto these small-scale problems, convinced that they’ll reveal the flaws inherent to dark matter and reveal a deeper truth.

According to models and simulations, all galaxies should be embedded in dark matter halos, whose densities peak at the galactic centers. On long enough timescales, of perhaps a billion years, a single dark matter particle from the outskirts of the halo will complete one orbit. The effects of gas, feedback, star formation, supernovae, and radiation all complicate this environment, making it extremely difficult to extract universal dark matter predictions, but the biggest problem may be that the cuspy centers predicted by simulations are nothing more than numerical artifacts. (NASA, ESA, AND T. BROWN AND J. TUMLINSON (STSCI))

If this new paper is correct, however, the only flaw is that cosmologists have taken one of the earliest simulation results — that dark matter forms halos with cusps at the center — and believed their conclusions prematurely. In science, it’s important to check your work and to have its results checked independently. But if everyone’s making the same error, these checks aren’t independent at all.

Disentangling whether these simulated results are due to the actual physics of dark matter or the numerical techniques we’ve chosen could put an end to the biggest debate over dark matter. If it’s due to actual physics after all, the core-cusp problem will remain a point of tension for dark matter models. But if it’s due to the technique we use to simulate these halos, one of cosmology’s biggest controversies could evaporate overnight.

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.