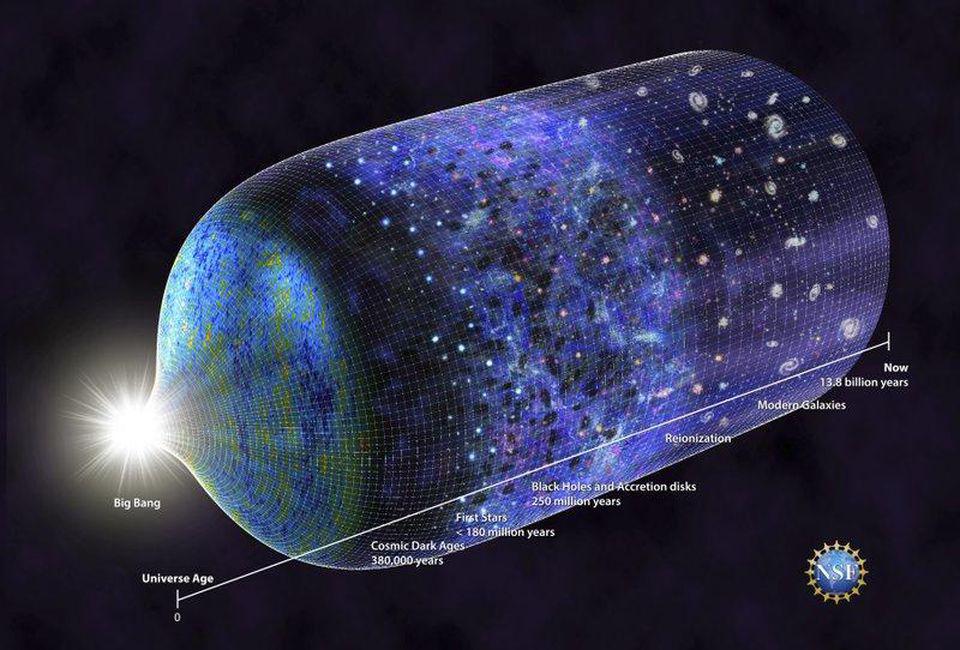
Cosmic inflation solves the “past hypothesis” problem

Right now, at this very moment, the total amount of entropy contained within the observable Universe is greater than it’s ever been before. Tomorrow’s entropy will be even greater, while yesterday, the entropy wasn’t quite as great as it is today. With each passing moment, inevitably, the Universe inches closer to a maximum entropy state known as the “heat death” of the Universe: a situation where all the particles and fields have reached their lowest-energy, equilibrium state, and no further energy can be extracted to perform any useful, order-creating tasks.

The reason for this is as simple as it is inevitable: the second law of thermodynamics. It states that the entropy of a closed, self-contained system can only increase or, in the ideal case, stay the same over time; it can never go down. It has a preferred direction for time: forward, as systems always tend toward greater (or even maximal) entropy over time. Commonly thought of as “disorder,” it seems to take our Universe toward a more chaotic state over time.

So how, then, did we — very ordered beings — emerge from this chaos? And if entropy has always been increasing, how did the Universe begin with an entropy that’s so much smaller than it is today? That’s the key to understanding the past hypothesis puzzle, and, beyond that, how cosmic inflation solves it.

In the earliest stages of the hot Big Bang, there were no bound structures that could form, only a “primordial soup” of matter particles, antimatter particles, and bosons like the photon. This hot, dense, and rapidly expanding state would quickly cool off.

There’s a common misconception that entropy, at a fundamental level, is synonymous with the concept of disorder. Take a room full of particles, for instance, where half of the particles are cold (low in kinetic energy, moving slowly, with a long timescale in between collisions) and half of the particles are hot (high in kinetic energy, moving rapidly, with short timescales separating collisions). You can imagine that you have two possible setups:

1. one where all the cold particles are shunted to one half of the room while the hot particles are kept on the other half of the room,
2. and one where the room isn’t divided into halves, but where the hot and cold particles are free to mix together.

The first case is, in fact, the lower entropy case, while the second represents the higher-entropy case. But this isn’t because “one is more ordered and one is more disordered,” but rather because in the first case there are fewer ways to arrange your particles to achieve this particular state, and in the second case, there are greater numbers of ways to arrange your particles so that this state is achieved.

If you had particles separated into hot-and-cold halves and removed the divider, they’d spontaneously mix together, producing a uniform-temperature state across all particles in short order. But if you have mixed-together particles of all temperatures and speeds, they would pretty much never separate themselves into a “hot half” and a “cold half.” It’s just too statistically unlikely.

A system set up in the initial conditions on the left and allowed to evolve will have less entropy if the door remains closed than if the door is opened. If the particles are allowed to mix, there are more ways to arrange twice as many particles at the same equilibrium temperature than there are to arrange half of those particles, each, at two different temperatures.

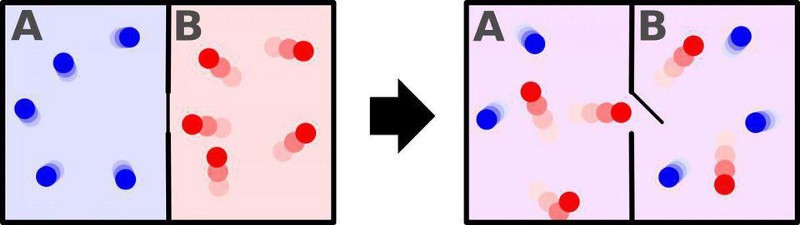
But there’s something else that can occur if you begin with the lower-entropy state (hot particles on one side of a divider and cold particles on the other side) and then allow it to spontaneously transition to a higher-entropy state: work, a form of energy, can not only be extracted, but that energy can then be put to use. Whenever you have a gradient — from high temperatures/energies/speeds to lower ones, for example — that’s a form of potential energy that, as it gets turned into the energy of motion, can be used to accomplish certain tasks.

The very act of extracting energy from those gradients and feeding off of it, in some variety, is what fuels all life processes at their core. The Universe, by starting off hot and dense some 13.8 billion years ago, and then expanding, cooling, and gravitating ever since, has been able to produce all sorts of ordered systems:

• galaxies,
• stars,
• heavy elements,
• stellar systems,
• planets,
• organic molecules,
• and even living organisms,

by feeding off of the released energy from processes where entropy, overall, increases.

A wine glass, when vibrated at the right frequency, will shatter. This is a process that dramatically increases the entropy of the system, and is thermodynamically favorable. The reverse process, of shards of glass reassembling themselves into a whole, uncracked glass, is so unlikely that it never occurs spontaneously in practice. However, wherever enough free, usable energy is present, disordered systems can become ordered, but only at the expense of increasing the overall entropy of the total system(s) in contact with one another.

This isn’t merely a qualitative statement. Based on the known particle content of the Universe and the size of the observable Universe — determined by the properties of the hot Big Bang and the fundamental constants of the Universe, including the speed of light — we can express the entropy of the Universe (S) in terms of Boltzmann’s constant, k_B. At the start of the Big Bang, radiation was the dominant form of entropy, and the total entropy of the observable Universe was S ~ 10⁸⁸ k_B. Although that might seem like a “big number,” things can only be quantified as large or small relative to something else.

Today, for example, the entropy of the observable Universe is much greater: about a quadrillion times as large. A responsible estimate places it somewhere around S ~ 10¹⁰³ k_B, where most of today’s entropy is caused by black holes. In fact, if we calculated only the entropy of the Milky Way and all the stars, gas, planets, life forms, and black holes present within it, we’d find that the entropy of the Milky Way was dominated by our galaxy’s largest supermassive black hole, with an entropy of S ~ 10⁹¹ k_B all on its own! In terms of entropy, our one meagre supermassive black hole defeats the entire visible Universe, combined, from 13.8 billion years ago!

This is the first image of Sgr A*, the supermassive black hole at the center of our galaxy. It’s the first direct visual evidence of the presence of this black hole. It was captured by the Event Horizon Telescope (EHT), an array which linked together eight existing radio observatories across the planet to form a single “Earth-sized” virtual telescope. Its measured mass of 4.3 million solar masses places it among the smallest supermassive black holes of all, and it possesses an entropy of ~10^91 k_B, or about 1000 times as much entropy as was contained in the observable Universe some 13.8 billion years ago.

As we continue to move forward in time, entropy continues to increase. Over not only billions but over the coming trillions, quadrillions, and quintillions of years ahead of us (and more), the Universe will:

• complete its nuclear fusion reactions inside the cores of stars,
• settle down into bound galaxy groups eternally separated by the ever-expanding Universe,
• expel gas and dust into the intergalactic medium,
• gravitationally eject planets, clumps of mass, and stellar remnants,
• create large numbers of black holes that will eventually grow to possess a maximum-valued mass,
• and then Hawking radiation takes over, leading to black hole decay.

After perhaps 10¹⁰³ years go by, the Universe will reach its maximal entropy value of around S = 10¹²³ k_B, or a factor of 100 quintillion greater than the entropy today. As even the most supermassive black holes decay into radiation, the entropy remains largely constant, only increasing slightly, but at this point there will be no more energy to extract. With the decay of the final black hole in the Universe, there will only be a cold bath of radiation permeating the cosmos, occasionally coming across a bound, degenerate, stable object like an atomic nucleus or another lonely, fundamental particle. With no further energy left to extract, and no less-common set of arrangements of particles that will spontaneously arise, the Universe will reach a state known as a heat death: a state of maximum entropy given the particles that exist.

As the Universe continues to age, the last sources of light will arise from the evaporation of black holes. While the least massive black holes will complete their evaporation after only 10^67 years or so, the most massive ones will persist for over a googol (10^100) years, making them the last objects to emit light, as far as we know.

That, in terms of entropy at least, is what the history of our Universe looks like. After starting from a hot, dense, nearly uniform, energetic, particle-and-antiparticle-filled state with a finite and measurable amount of entropy in it, the Universe:

• expands,
• cools,
• gravitates,
• forms structure on a variety of scales,
• which leads to processes that become wildly complex,
• leading to star systems, planets, biological activity, and life,
• and then it all decays away,

leading to a maximum entropy state from which no further energy can be extracted. All told, from the Big Bang until the eventual heat death, the entropy of our Universe increases by a factor of ~10³⁵, or 100 decillion: the same as the number of atoms it takes to make up approximately 10 million human beings.

But here’s where the big question regarding the past hypothesis comes in: if each passing moment brings along with it an increase in entropy, and the entropy of the Universe has always been increasing, and the second law of thermodynamics dictates that entropy must always increase (or remain the same) and can never decrease, then how did it start off in such a low-entropy state to begin with?

The answer, perhaps surprisingly, has been known theoretically for more than 40 years: cosmic inflation.

Exponential expansion, which takes place during inflation, is so powerful because it is relentless. With every ~10^-35 seconds (or so) that passes, the volume of any particular region of space doubles in each direction, causing any particles or radiation to dilute and causing any curvature to quickly become indistinguishable from flat. This also plays a role in keeping the entropy constant, but dramatically lowering the entropy density.

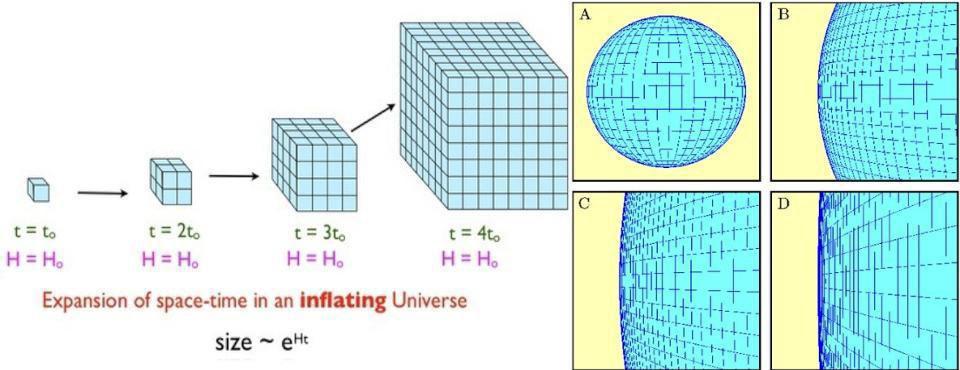
You might think of cosmic inflation alternately, as the reason the Big Bang occurred, the additional, now-verified hypothesis of what came before and set up the conditions that the Big Bang was born with, or as the theory that removed the notion of the “Big Bang singularity” from the notion of the hot, dense, expanding state we identify as the Big Bang. (All are correct in their own ways.) But inflation, although it’s a little appreciated feature of it, by its very nature forces the Universe to be born in a low entropy state, regardless of the conditions from which inflation arose. And even more remarkably, it never once violates the second law of thermodynamics, allowing entropy to never decrease during the process.

How does this occur?

The simplest way to explain it is to introduce two concepts to you that you likely have already heard of, but perhaps don’t have a sufficient appreciation of. The first is the difference between entropy (the total amount you’ll find) and entropy density (the total amount you’ll find in a given volume of space), which sounds easy enough. But the second requires a little bit of an explanation: the concept of adiabatic expansion. Adiabatic expansion is an important property in thermodynamics, in engines, and also in the expanding Universe.

This schematic of an engine shows how the rapid compression of air due to a piston’s motion, adiabatic compression, leads to increased temperatures and, if there’s enough of a fuel/air mixture inside the compressing piston, ignition followed by combustion, which causes the chamber to re-expand. This is the fundamental principle behind an internal combustion engine.

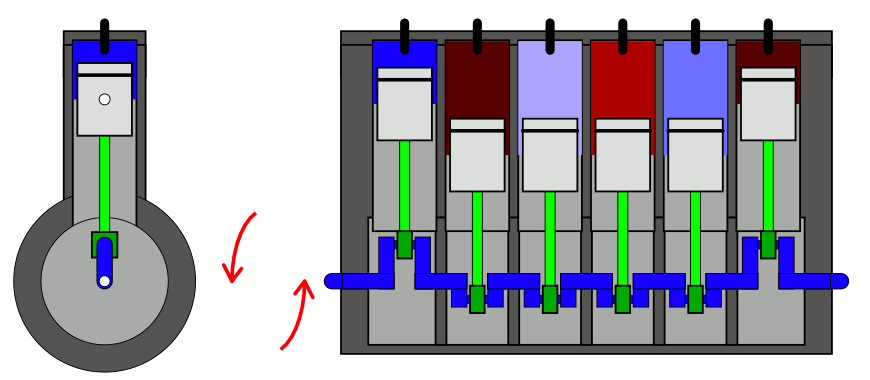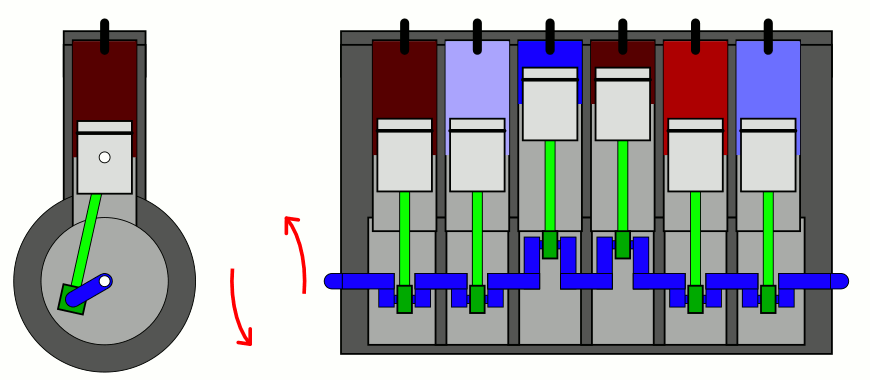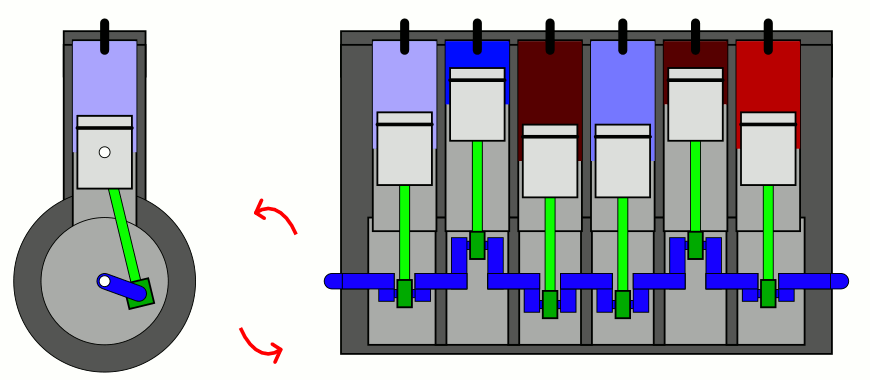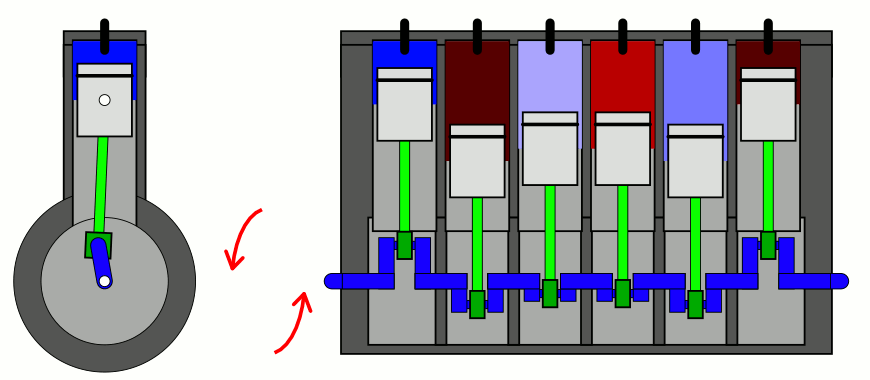
You might remember — going all the way back to when you first learned about chemistry — that a sealed container full of gas will have certain properties inside of it that are fixed, like the number of particles inside, and other properties that can vary, like the pressure, temperature, or volume of the gas inside that container. Depending on how you change one or more of those properties, the others will change in response in a variety of interesting ways.

• You can increase or decrease the volume of the container while holding the pressure constant, resulting in a temperature change that obeys Charles’s Law: an example of isobaric expansion or contraction.
• You can increase or decrease the pressure of the container while keeping the volume constant, resulting in a temperature change: an example of isovolumetric changes.
• You can keep the temperature constant while slowly either increasing or decreasing the volume, resulting in a pressure change that obeys Boyle’s law: an isothermal change.

But if you take a confined gas and either very rapidly expand it or very rapidly compress it, all three of those factors — pressure, volume, and temperature alike — will all change. This type of change is known as an adiabatic change, where adiabatic expansion leads to rapid cooling and adiabatic contraction leads to rapid heating, where the latter is how pistons work. No heat is exchanged between the outside environment and the internal system, but there is a key quantity that remains constant during adiabatic expansion or contraction: entropy. In fact, “isentropic,” or constant entropy, is a synonym for adiabatic if the system obeys time-reversal symmetry as well.

This diagram shows, to scale, how spacetime evolves/expands in equal time increments if your Universe is dominated by matter, radiation, or the energy inherent to space itself (i.e., during inflation or dark energy dominance), with the latter corresponding to the inflationary phase that preceded and set up the hot Big Bang. Although all of these model universes expand toward infinite size, they approach it at different rates, with the “space itself” solution approaching infinity in a fundamentally more quick fashion than the other two.

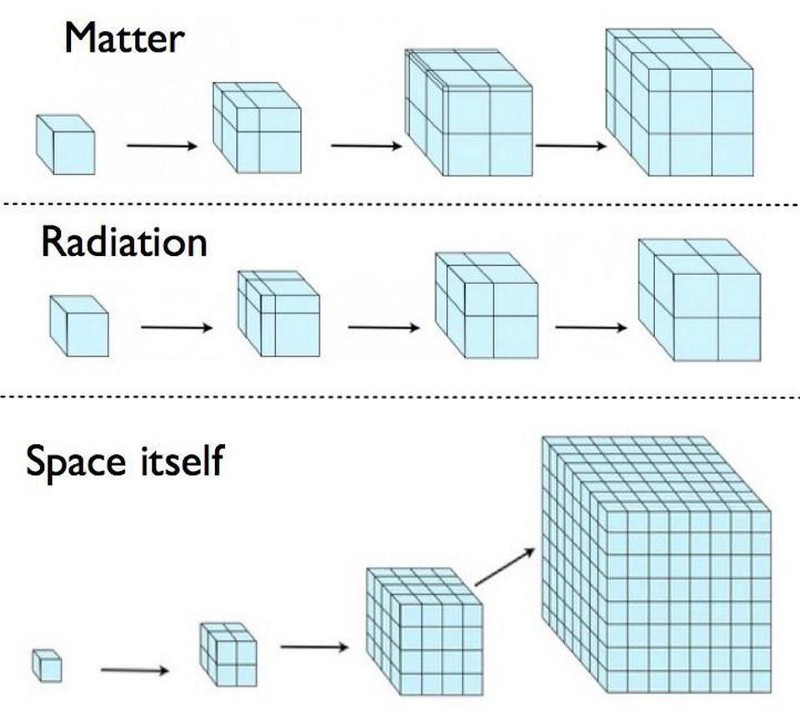
During cosmic inflation, some portion of the Universe begins expanding in a rapid, constant fashion, resulting in exponential behavior. In one “doubling time,” which is typically a fraction of a decillionth of a second, the length, width, and depth (all three dimensions) all double in size, increasing the volume by a factor of 8. After a second “doubling time,” they all double again, increasing the original volume by a factor of 64.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

After 10 doubling times go by, the patch of Universe that’s undergone inflation has increased in volume by more than a factor of a billion. After 100 doubling times, its volume has increased by a factor of something like ~10⁹⁰. And after 1000 doubling times, its volume has increased by a great enough amount that it would have taken a Planck-sized volume, the smallest volume that makes physical sense in a quantum Universe, and stretched it to well beyond the size of the visible Universe.

And all the while, the entropy within that volume, because the Universe expands adiabatically, remains constant. In other words, the total entropy doesn’t decrease, but during inflation, the entropy density drops exponentially. This ensures that, when inflation ends, the majority of entropy in the volume of the Universe that becomes our observable Universe comes from the end of inflation and the onset of the hot Big Bang, not from whatever entropy pre-existed in the Universe during or prior to inflation.

The analogy of a ball sliding over a high surface is when inflation persists, while the structure crumbling and releasing energy represents the conversion of energy into particles, which occurs at the end of inflation. This transformation — from inflationary energy into matter and radiation — represents an abrupt change in the expansion and properties of the Universe, as well as a tremendous increase in entropy wherever inflation ends.

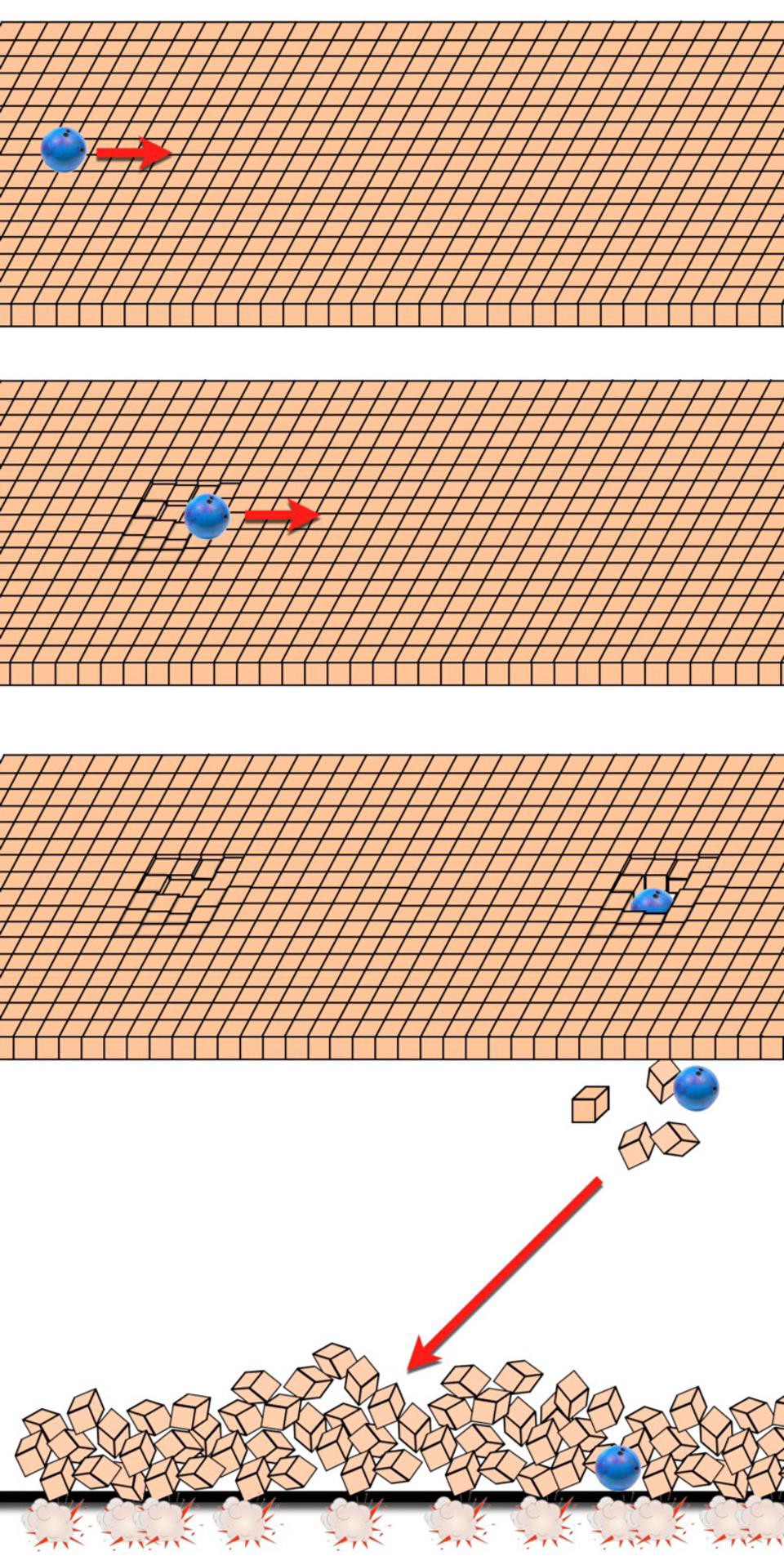
In other words, the solution to the problem of the past hypothesis, or why the Universe possessed a low-entropy state at the start of the hot Big Bang, is because the Universe underwent a period of cosmic inflation. The rapid, relentless, exponential expansion of the Universe took whatever the entropy was in a specific region of space — a certain volume of space — and inflated that volume to tremendous quantities.

Even though entropy was conserved (or possibly increased very, very slightly), the entropy density plummets, as near-constant entropy in an exponentially expanding volume translates to having the entropy in any specific region of space becoming exponentially suppressed. That’s why, if you accept the evidence in favor of cosmic inflation, and that evidence is very, very good, you no longer have a “past hypothesis” problem. The Universe is simply born with the amount of entropy that the transition from an inflationary state to a hot Big Bang state, a process known as cosmic reheating, imprints upon it.

The Universe was born in a low-entropy state because inflation caused the entropy density to plummet, and then the hot Big Bang occurred, with entropy forever increasing from that point on. As long as you remember that entropy is not entropy density, you’ll never be confused by the past hypothesis again.