Why black holes spin at nearly the speed of light

Whenever you take a look out there at the vast abyss of the deep Universe, it’s the points of light that stand out the most: stars and galaxies. While the majority of the light that you’ll first notice does indeed come from stars, a deeper look, going far beyond the visible portion of the electromagnetic spectrum, shows that there’s much more out there. The brightest, most massive stars, by their very nature, have the shortest lifespans, as they burn through their fuel far more quickly than their lower-mass counterparts. Once they’ve reached their limits and can fuse elements no further, they reach the end of their lives and become stellar corpses.

These corpses come in multiple varieties: white dwarfs for the lowest-mass (e.g., Sun-like) stars, neutron stars for the next tier up, and black holes for the most massive stars of all. These compact objects give off electromagnetic emissions spanning wavelengths from radio to X-ray light, revealing properties that range from mundane to absolutely shocking. While most stars themselves may spin relatively slowly, black holes rotate at nearly the speed of light. This might seem counterintuitive, but under the laws of physics, it couldn’t be any other way. Here’s why.

The Sun’s light is due to nuclear fusion, which primarily converts hydrogen into helium. When we measure the rotation rate of the Sun, we find that it’s one of the slowest rotators in the entire Solar System, taking from 25-to-33 days to make one 360-degree rotation, dependent on latitude. Emitting a near-constant 3.8 × 10^26 W of power, the Sun is the brightest thing most of us will ever see. Although many other sources are intrinsically brighter, they’re much farther away.

The closest analogue we have to one of those extreme objects in our own Solar System is the Sun. In another 7 billion years or so, after becoming a red giant and burning through the helium fuel that’s built up within its core, it will end its life by blowing off its outer layers while its core contracts down to a stellar remnant: the most gentle of all major types of stellar death.

The outer layers will create a sight known as a planetary nebula, which comes from the blown-off gases getting ionized and illuminated from the contracting central core. This nebula will glow for tens of thousands of years before cooling off and becoming neutral again, generally returning that material to the interstellar medium. When the opportunity then arises, those processed atoms will participate in future generations of star formation.

But the inner core, largely composed of carbon and oxygen, will contract down as far as it possibly can. In the end, gravitational collapse will only be stopped by the particles ⁠ — atoms, ions, and electrons ⁠ — that the remnant of our Sun will be made of.

When our Sun runs out of fuel, it will become a red giant, followed by a planetary nebula with a white dwarf at the center. The Cat’s Eye nebula is a visually spectacular example of this potential fate, with the intricate, layered, asymmetrical shape of this particular one suggesting a binary companion. At the center, a young white dwarf heats up as it contracts, reaching temperatures tens of thousands of Kelvin hotter than the surface of the red giant that spawned it. The outer shells of gas are mostly hydrogen, which gets returned to the interstellar medium at the end of a Sun-like star’s life.

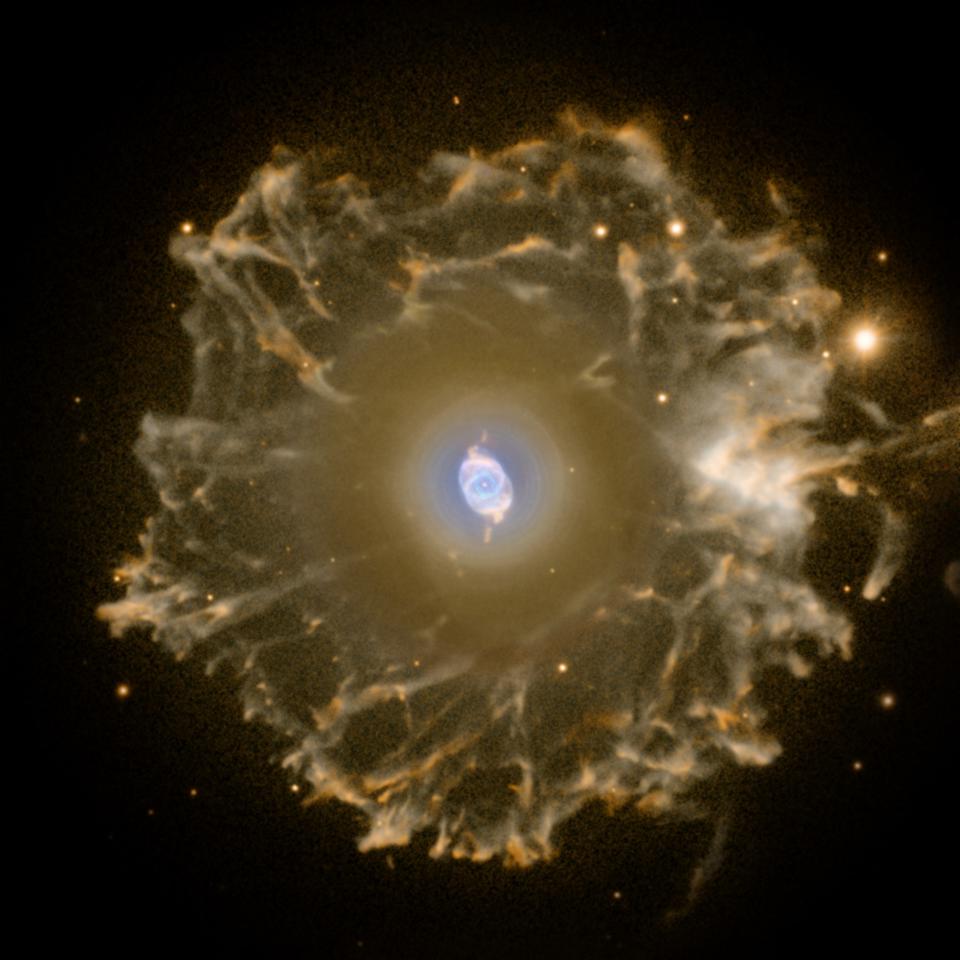
So long as you remain below a critical mass threshold, the Chandrasekhar mass limit, the quantum properties inherent to those particles will be sufficient to hold the stellar remnant up against gravitational collapse. The endgame for a Sun-like star’s core will be a degenerate state known as a white dwarf. It will possess a sizable fraction of the mass of its parent star, but crammed into a tiny fraction of the volume: approximately the size of Earth.

Astronomers now know enough about stars and stellar evolution to describe what happens during this process. For a star like our Sun, approximately 60% of its mass will get expelled in the outer layers, while the remaining 40% remains in the core. The more massive a star becomes, the more mass, percentage-wise, gets blown off in its outer layers, with less being retained in the core. For the most massive stars that suffer the same fate as our Sun, possessing about 7-8 times the Sun’s mass, the mass fraction remaining in the core comes all the way down to about 18% of the original star’s mass.

This has happened nearby relatively recently, as the brightest star in Earth’s sky, Sirius, has a white dwarf companion, visible in the Hubble image below.

This image shows Sirius A and B, a bluer and brighter star than our Sun and a white dwarf star, respectively, as imaged by the Hubble space telescope. Sirius B, like all white dwarf stars that exist at present, is composed of elements like carbon, oxygen, neon, calcium, and magnesium. But in the future, helium white dwarfs will come to exist as well: spawned from the remnants of fully convective red dwarf stars.

Sirius A is a little bit brighter and more massive than our Sun, and we believe that its binary companion, Sirius B, was once even more massive than Sirius A. Because the more massive stars burn through their nuclear fuel more quickly than lower-mass ones, Sirius B likely ran out of fuel some time ago. Today, Sirius A remains burning through its hydrogen fuel, and dominates that system in terms of mass and brightness. While Sirius A, today, weighs in at about twice the mass of our Sun, Sirius B is only approximately equal to our Sun’s mass.

However, based on observations of the white dwarfs that happen to pulse, we’ve learned a valuable lesson. Rather than taking multiple days or even (like our Sun) approximately a month to complete a full rotation, like normal stars tend to do, white dwarfs complete a full 360° rotation in as little as an hour. This might seem bizarre, but if you’ve ever seen a figure skating routine, the same principle that explains a spinning skater who pulls their arms in explains the white dwarfs rotational speed: the law of conservation of angular momentum.

When a figure skater like Yuko Kavaguti (pictured here from 2010’s Cup of Russia) spins with her limbs far from her body, her rotational speed (as measured by angular velocity, or the number of revolutions-per-minute) is lower than when she pulls her mass close to her axis of rotation. The conservation of angular momentum ensures that as she pulls her mass closer to the central axis of rotation, her angular velocity speeds up to compensate.

Angular momentum is simply a measure of “How much rotational and/or orbital motion does a mass have to it?” If you puff that massive object up so that its mass is farther from its rotational center, it has to slow down in its rotational speed in order to conserve angular momentum. Similarly, if you compress a massive object down, so that more of its mass is closer to the center of its axis-of-rotation, it will have to speed up in its rotational speed, making more revolutions-per-second, to keep angular momentum conserved.

What happens, then, if you were to take a star like our Sun — with the mass, volume, and rotation speed of the Sun — and compressed it down into a volume the size of the Earth: a typical size for a white dwarf?

Believe it or not, if you make the assumption that angular momentum is conserved, and that both the Sun and the compressed version of the Sun we’re imagining are spheres, this is a completely solvable problem with only one possible answer. If we go conservative, and assume the entirety of the Sun rotates once every 33 days (the longest amount of time it takes any part of the Sun’s photosphere to complete one 360° rotation) and that only the inner 40% of the Sun becomes a white dwarf, you get a remarkable answer: the Sun, as a white dwarf, will complete a rotation in just 25 minutes.

When lower-mass, Sun-like stars run out of fuel, they blow off their outer layers in a planetary nebula, but the center contracts down to form a white dwarf, which takes a very long time to fade to darkness. The planetary nebula our Sun will generate should fade away completely, with only the white dwarf and our remnant planets left, after approximately 9.5 billion years. The white dwarf will rotate far, far faster than our Sun presently does.

By bringing all of that mass close in to the stellar remnant’s axis of rotation, we ensure that its rotational speed must rise. In general, if you halve the radius that an object has as it rotates, its rotational speed increases by a factor of four; rotational speed is inversely proportional to the square of a rotating mass’s radius. If you consider that it takes approximately 109 Earths to go across the diameter of the Sun, you can derive the same answer for yourself. (In reality, white dwarfs generally rotate a little more slowly, as the outermost layers get blown off, and only the interior “core” material contracts down to form a white dwarf.)

Unsurprisingly, then, you might start to ask about neutron stars or black holes: even more extreme objects. A neutron star is typically the product of a much more massive star ending its life in a supernova, where the particles in the core get so compressed that it behaves as one giant atomic nucleus composed almost exclusively (90% or more) of neutrons. Neutron stars are typically twice the mass of our Sun, but just about 10-to-40 km across. They rotate far more rapidly than any known star or white dwarf ever could.

The two best-fit models of the map of the neutron star J0030+0451, constructed by the two independent teams who used the NICER data, show that either two or three ‘hot spots’ can be fitted to the data, but that the legacy idea of a simple, bipolar field cannot accommodate what NICER has seen. This neutron star measures just ~12 km across, and are both the densest non-singular objects in the Universe and also the hottest at their surfaces.

Even the most naïve estimate you could make for the rotational speed of a neutron star — again, in analogy with our Sun — illustrates just how rapidly we can expect a neutron star to spin. If you repeated the thought experiment of compressing the entire Sun down into a smaller volume, but this time used one that was merely 40 kilometers in diameter, you’d get a much, much more rapid rotation rate than you ever could for a white dwarf: about 10 milliseconds. That same principle that we previously applied to a figure skater, about the conservation of angular momentum, leads us to the conclusion that neutron stars could complete more than 100 full rotations in a single second.

In fact, this lines up perfectly with our actual observations. Some neutron stars emit radio pulses along Earth’s line-of-sight to them: pulsars. We can measure the pulse periods of these objects, and while some of them take approximately a full second to complete a rotation, some of them rotate in as little as 1.3 milliseconds, up to a maximum of 766 rotations-per-second.

This computer simulation of a neutron star shows charged particles being whipped around by a neutron star’s extraordinarily strong electric and magnetic fields. The fastest-spinning neutron star we’ve ever discovered is a pulsar that revolves 766 times per second: faster than our Sun would spin if we collapsed it down to the size of a neutron star. Irrespective of their spin rates, neutron stars may be the densest physical objects nature can create without progressing to create a singularity, and typically have surface temperatures of several hundreds of thousands of degrees.

The fastest-spinning neutron stars known are called millisecond pulsars, and they really do rotate at incredibly fast speeds. At their surfaces, those rotation rates are indeed relativistic: meaning they reach speeds that are a significant fraction of the speed of light. The most extreme examples of such neutron stars can reach speeds exceeding 50% the speed of light at the outer surface of these neutron stars.

But that doesn’t even approach the true astrophysical limits found in the Universe. Neutron stars aren’t the densest objects in the Universe; that honor goes to black holes, which take all the mass you’d find in a neutron star — more, in fact — and compress it down into a region of space where even an object moving at the speed of light couldn’t escape from it.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

If you compressed the Sun down into a volume just 3 kilometers in radius, that would force it to become a black hole. And yet, the conservation of angular momentum would mean that much of that internal region would experience frame-dragging so severe that space itself would get dragged at speeds approaching the speed of light, even outside of the Schwarzschild radius of the black hole. The more you compress that mass down, the faster the fabric of space itself gets dragged.

When a massive enough star ends its life, or two massive enough stellar remnants merge, a black hole can form, with an event horizon proportional to its mass and an accretion disk of infalling matter surrounding it. When the black hole rotates, the space both outside and inside the event horizon rotates, too: this is the effect of frame-dragging, which can be enormous for black holes.

Realistically, we can’t measure the frame-dragging of space itself in the vicinity of a black hole. But we can measure the frame-dragging effects on the matter that happens to be present within that space. For black holes, that means looking at the accretion disks and accretion flows found around these black holes that exist in matter-rich environments. Perhaps paradoxically, the smallest mass black holes, which have the smallest event horizons, actually have the largest amounts of spatial curvature at and near their event horizons.

You might think, therefore, that they’d make the best laboratories for testing these frame dragging effects. But nature surprised us on that front: a supermassive black hole at the center of galaxy NGC 1365 — which also happens to be one of the first galaxies imaged by the James Webb Space Telescope — has had the radiation emitted from the volume outside of it detected and measured, revealing its speed. Even at these large distances, the material spins at 84% the speed of light. If you insist that angular momentum be conserved, it couldn’t have turned out any other way.

In the vicinity of a black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. Unlike in the non-rotating case, the event horizon splits into two, while the central singularity gets stretched out into a one-dimensional ring. Nobody knows what occurs at the central singularity, but its presence and existence cannot be avoided with our current understanding of physics.

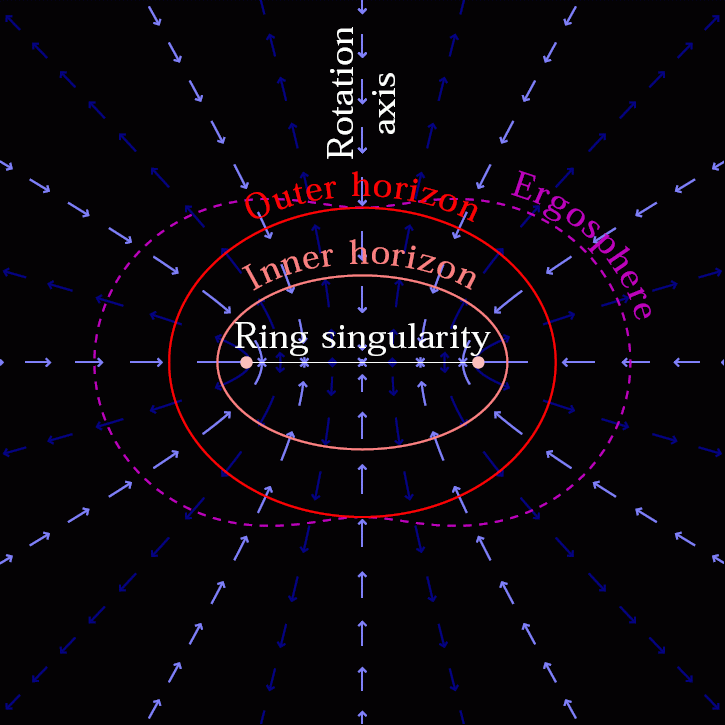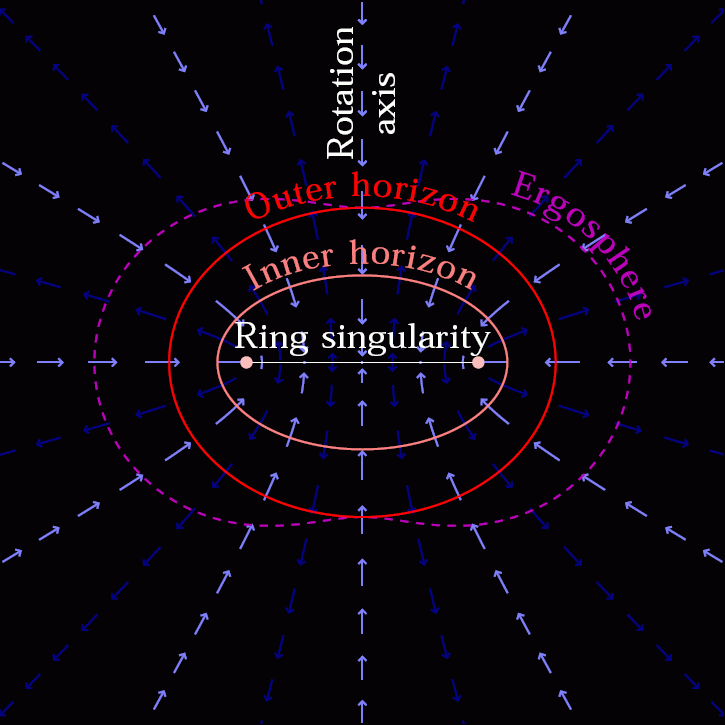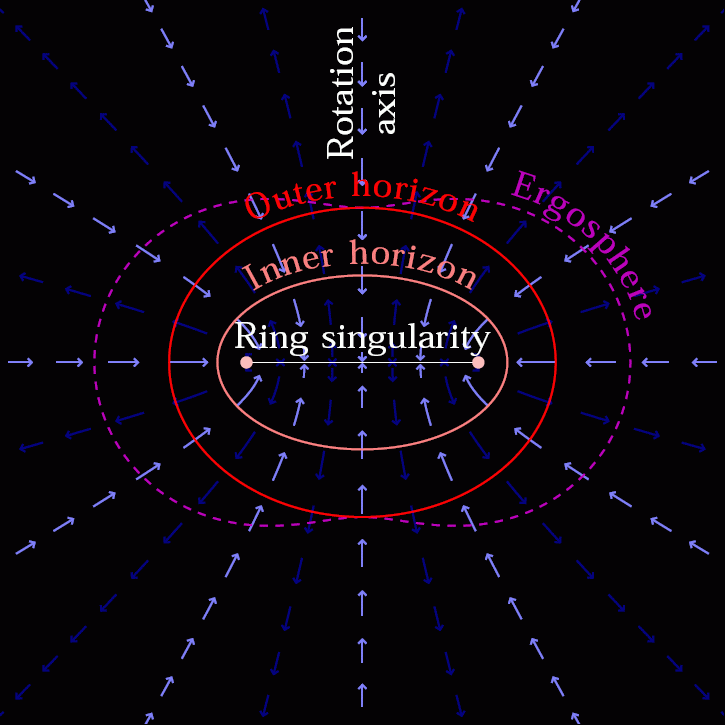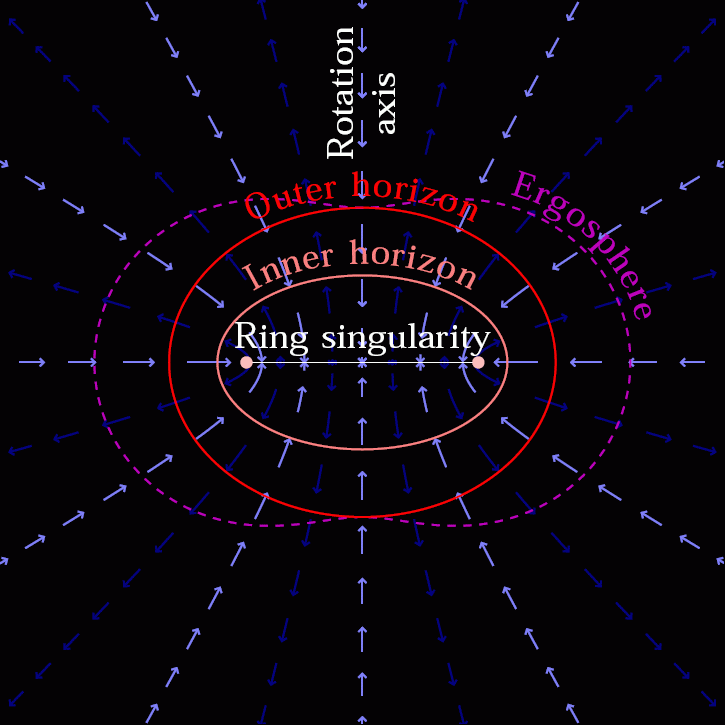
Subsequently, we’ve inferred the spins of black holes that have merged together with gravitational wave observatories such as LIGO and Virgo, and found that some black holes spin at the theoretical maximum: around ~95% the speed of light. It’s a tremendously difficult thing to intuit: the notion that black holes should spin at almost the speed of light. After all, the stars that black holes are built from rotate extremely slowly, even by Earth’s standards of one rotation every 24 hours. Yet if you remember that most of the stars in our Universe also have enormous volumes, you’ll realize that they contain an enormous amount of angular momentum.

If you compress that volume down to be very small, those objects have no choice. If angular momentum has to be conserved, all they can do is spin up their rotational speeds until they almost reach the speed of light. At that point, gravitational waves will kick in, and some of that energy (and angular momentum) gets radiated away, bringing it back down to below the theoretical maximum value. If not for those processes, black holes might not be black after all, instead revealing naked singularities at their centers. In this Universe, black holes have no choice but to rotate at extraordinary speeds. Perhaps someday, we’ll be able to measure their rotation directly.