Astrophysics Signal Does What The LHC Cannot: Constrain Quantum Gravity And String Theory

Astrophysics has probed a test of a fundamental law, ‘Lorentz invariance,’ well beyond the LHC’s limits. Einstein is still right.

The greatest scientific legacy that Albert Einstein left us is this: that the speed of light, and the laws of physics, appear to be the same for all observers in the Universe. Regardless of where you’re located, how fast or in which direction you’re moving, or when you’re performing your measurements, everyone experiences the same fundamental rules of nature. The symmetry that underlies this, Lorentz invariance, is the one symmetry that must never be violated.

However, many ideas that go beyond the Standard Model and General Relativity — such as string theory or most manifestations of quantum gravity — could break this symmetry, with consequences for what we’d observe about the Universe. A new study by the HAWC collaboration, just published on March 30, 2020, just placed the tightest constraints on Lorentz invariance violation ever, with fascinating implications for theoretical physics.

The idea of unification holds that all three of the Standard Model forces, and perhaps even gravity at higher energies, are unified together in a single framework. This idea is powerful, has led to a great deal of research, but is a completely unproven conjecture. At even higher energies, a quantum theory of gravity could potentially unify all of the forces. But such scenarios often have consequences for observable, lower-energy phenomena that are tightly constrained. (© ABCC AUSTRALIA 2015 WWW.NEW-PHYSICS.COM)

Our best physical theories of the Universe are the Standard Model, which describes the fundamental particles and the nuclear and electromagnetic interactions between them, and General Relativity, which describes spacetime and gravitation. Although these two theories describe reality perfectly, they’re not complete: they do not describe, for example, how gravity behaves at a quantum level.

The hope among physicists — what some would call its ultimate dream or “holy grail” — is that there exists a quantum theory of gravity, and that this theory, when we find it, will unify all of the Universe’s forces together under one single framework. But many of these proposed quantum gravity frameworks, including string theory, can break that fundamental symmetry that’s important to both the Standard Model and General Relativity: Lorentz invariance.

Different frames of reference, including different positions and motions, would see different laws of physics (and would disagree on reality) if a theory is not relativistically invariant. The fact that we have a symmetry under ‘boosts,’ or velocity transformations, tells us we have a conserved quantity: linear momentum. The fact that a theory is invariant under any sort of coordinate or velocity transformation is known as Lorentz invariance, and any Lorentz invariant symmetry conserves CPT symmetry. However, C, P, and T (as well as the combinations CP, CT, and PT) may all be violated individually. (WIKIMEDIA COMMONS USER KREA)

Lorentz invariance is one of those physics terms that has a jargon-rich name, but a very simple meaning: the laws of nature are the same regardless of where or when you’re measuring them. It doesn’t matter if you’re here or a billion light-years away; it doesn’t matter if you’re making your measurements now or billions of years ago or billions of years in the future; it doesn’t matter if you’re at rest or moving close to the speed of light. If your laws don’t care about your position or motion, your theory is Lorentz invariant.

The Standard Model is exactly Lorentz invariant. General Relativity is exactly Lorentz invariant. But many incarnations of quantum gravity are only approximately Lorentz invariant. Either the symmetry that mandates it is broken, or there’s new physics that only appears at high-energy scales that breaks it. Although the low-energy Universe is observed to be Lorentz invariant, direct searches at particle colliders (like the LHC) are severely limited by the energies they can probe.

An aerial view of CERN, with the Large Hadron Collider’s circumference (27 kilometers in all) outlined. The same tunnel was used to house an electron-positron collider, LEP, previously. The particles at LEP went far faster than the particles at the LHC, but the LHC protons carry far more energy than the LEP electrons or positrons did. Strong tests of symmetries are performed at the LHC, but photon energies are well below what the Universe produces. (MAXIMILIEN BRICE (CERN))

In physics, we normally measure energies in terms of electron-volts (eV), or the amount of energy required to give a single electron an electric potential of 1 volt. In particle physics, we accelerate things to high energies, and so measure them in either GeV (a billion electron-volts) or TeV (a trillion electron-volts), depending on the energies we reach. The LHC reaches energies of around 7 TeV per particle, but that’s still very limited.

Typically, when physicists talk about the highest energy scales, they’re talking about either the theoretical grand unification scale, the string scale, or the Planck scale, the last of which is where the known laws of physics presently break down. These are between 10¹⁵ and 10¹⁹ GeV, or more than a trillion times the energies seen at the LHC. While the LHC is a great tool for making many constraints, it does a comparatively poor job of testing models of quantum gravity that might violate Lorentz invariance.

Pulsar wind nebulae, like the Crab Nebula depicted here in X-ray and optical light, are also the sources of not only very high energy particles, but extremely high-energy gamma-rays, which can be measured and used to constrain certain possible extensions to the Standard Model. (OPTICAL: NASA/HST/ASU/J. HESTER ET AL. X-RAY: NASA/CXC/ASU/J. HESTER ET AL.)

But astrophysics gives us a laboratory to probe far beyond the limits of what the LHC, or any Earth-based physics experiment, is likely to ever provide. Individual particles, in the form of cosmic rays, have been spotted with energies in excess of 10¹¹ GeV. Astrophysical phenomena like supernovae, pulsars, black holes, and active galactic nuclei can create conditions far more extreme, explosive, and energetic than our laboratories ever could.

And, perhaps most spectacularly, the astrophysical distances these particles need to cover ensure that we aren’t measuring their properties over timescales of a tiny fraction-of-a-second, but over the myriad of light-years they need to travel to reach our eyes. This combination of high-energy particles traveling over astronomical distances gives us an unprecedented laboratory for testing these Lorentz invariance violating ideas that quantum gravity and string theory models motivate.

Quantum gravity tries to combine Einstein’s general theory of relativity with quantum mechanics. Quantum corrections to classical gravity are visualized as loop diagrams, as the one shown here in white. Many symmetries that are mandated in the Standard Model could be only approximate symmetries in a theory of quantum gravity. (SLAC NATIONAL ACCELERATOR LABORATORY)

One particularly good test that we can perform is to look at photons — quanta of light — as they travel throughout the Universe. If Lorentz invariance is a perfect, exact symmetry, then all photons of all energies should propagate through the Universe, even across cosmic distances, equally. But if there are any violations of this symmetry, even if it’s at ultra-high energy scales well beyond the energy of those photons, then photons above a particular energy threshold should decay away.

In standard particle physics, every interaction must conserve both energy and momentum. Two photons can spontaneously interact and create an electron-positron pair, but one photon cannot do that on its own. If we demand that energy is conserved, the only way to conserve momentum is to have an additional particle come into play.

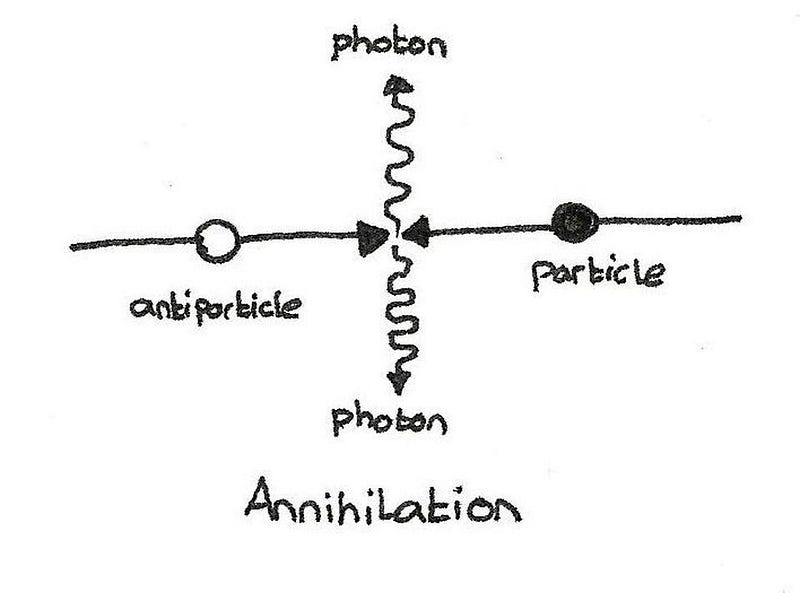
Two photons can collide, producing an electron-positron pair, or an electron-positron pair can interact, producing two photons. But you can’t get a pair from just one photon, since that would violate energy-momentum conservation. In a Lorentz invariance violating scenario, however, such a photon decay is not forbidden. (ANDREW DENISZCZYC, 2017)

But if Lorentz invariance is violated, we don’t need to conserve momentum exactly; only approximately. If the new effects that cause this violation come into play at some very high energy scale, that means there’s a certain probability that even lower-energy photons will experience a Lorentz invariance-violating decay. The effect is small, but over distances of thousands of light-years or more, the probability of photons above a certain energy threshold should drop to zero.

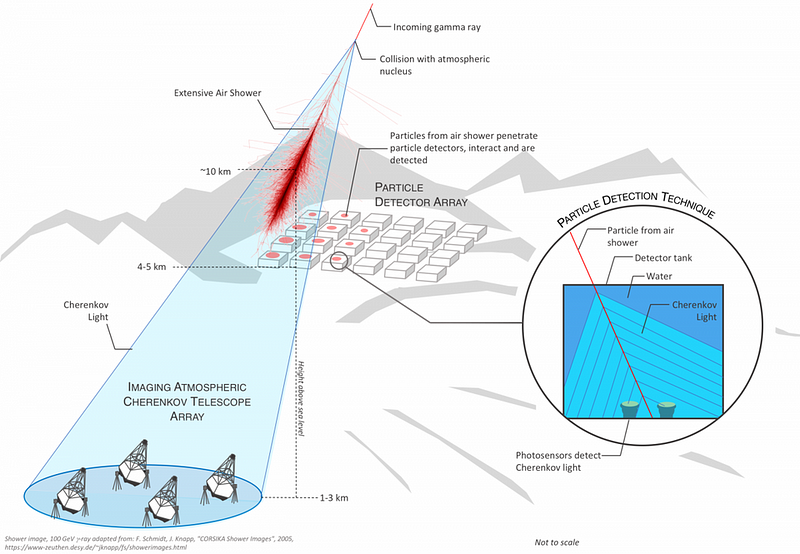
One of the most sophisticated tools astronomers use to measure these high energy gamma-ray photons is HAWC: the high altitude water Cherenkov observatory. Precise measurements of these very high energy photons — photons above 10 or even 100 TeV, about a hundred times the photon energies that the LHC can produce — can provide the strongest searches ever for Lorentz invariance violation.

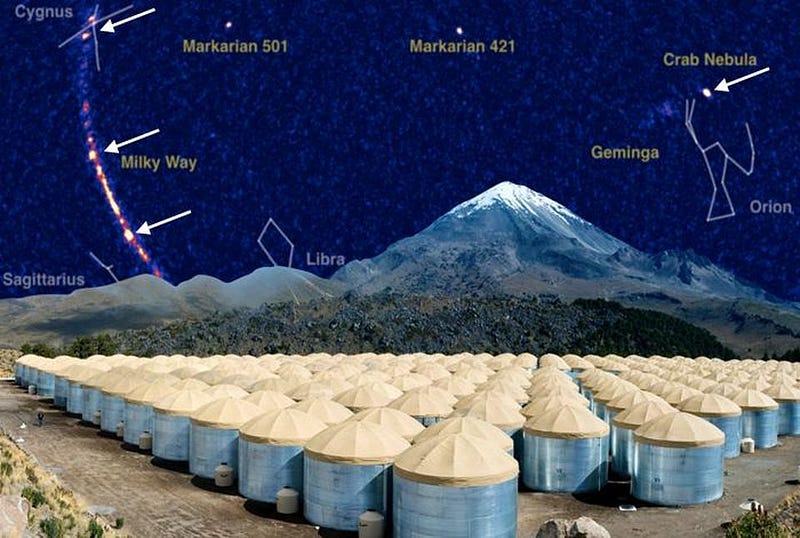
This compound graphic shows a view of the sky in ultra-high energy gamma rays. The arrows indicate the four sources of gamma rays with energies over 100 TeV from within our galaxy (courtesy of the HAWC collaboration) imposed over a photo of the HAWC Observatory’s 300 large water tanks. The tanks contain sensitive light detectors that measure showers of particles produced by the gamma rays striking the atmosphere more than 10 miles overhead. (JORDAN GOODMAN / HAWC COLLABORATION)

In their latest publication, the HAWC collaboration announced the detection of large numbers of these high-energy photons coming from four separate sources within the Milky Way: all corresponding to pulsar wind nebulae, the remnants of supernovae that accelerate material from the surrounding matter-rich regions.

If Lorentz invariance holds, there should be a continuous spectrum of these photons coming from these pulsars, without a hard cutoff (i.e., a steep drop and falloff) in their energy spectrum. But if Lorentz invariance is violated, then above a particular threshold, the number of photons should drop: either to 0 or to 50% of their expected value, depending on the particular Lorentz invariance violation scenario. But what HAWC saw, to a precision that’s almost 100 times better than any previous measurement, indicates no violation at all.

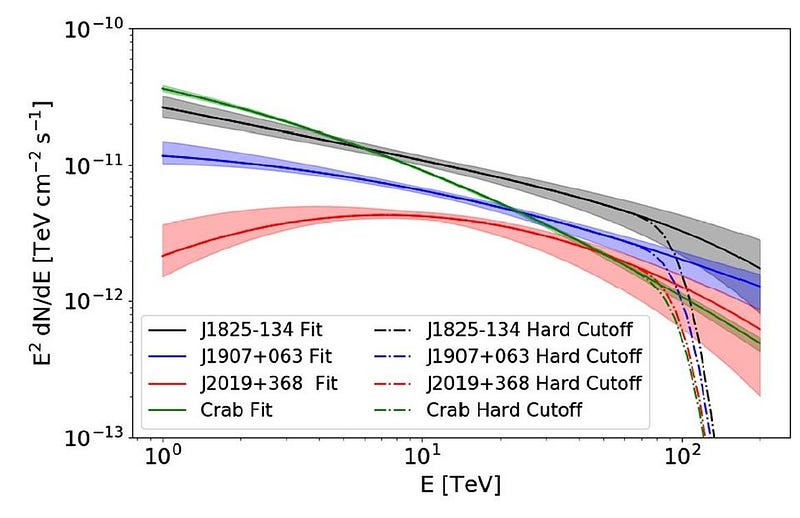
The four different pulsars observed by HAWC follow the colored solid lines (best fit) for their photon energy spectrum, with the uncertainty contours shown in shaded colors. The Lorentz invariance violating scenarios, shown with dotted lines, are ruled out. (A. ALBERT ET AL. (HAWC COLLABORATION), PHYS. REV. LETT. 124, 131101 (2020))

What’s fascinating about this result is that it sets a limit on the energy scale at which Lorentz invariance violation is allowed to take place. Based on the latest HAWC results, we can conclude that there are no violations of this symmetry up to an energy scale of 2.2 × 10³¹ eV: nearly 2,000 times the Planck energy scale.

This is, importantly, much higher than the energy scale at which string theory, quantum gravity, or any such exotic beyond-the-Standard Model physics scenarios that bring Lorentz invariance violation along with them. In the future, an even higher energy instrument could place even tighter constraints: both on the coupling and the energy scale of possible Lorentz violation, with future limits rising as the cube of the observed photon energy.

The proposed Southern Wide-field Gamma-ray Observatory (SWGO) could cover an energy range that extends well beyond what HAWC can reach; an improvement of a factor of 10 in energy would translate to an improvement of a factor of 1000 in the scale that Lorentz invariance violation can be constrained. (SWGO COLLABORATION)

Of course, there are always theoretical contortions one can invent to still allow for the possibility of Lorentz invariance violation. It could happen at an energy scale far higher than we’ve placed constraints on, thousands of times above the Planck scale. It could involve an extraordinarily small coupling, which would relax the energy constraints. Or it could involve a different type (e.g., subluminal) of Lorentz invariance violation than we typically assume.

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

But the fact remains that these photon-based constraints teach us that if a quantum gravity candidate such as string theory introduces a type of Lorentz invariance violation that predicts an astrophysical signature of photon decay, as many do, they are now constrained or even ruled out by this new set of observations. The laws of physics really are the same everywhere and at all times, and any extension to the Standard Model and General Relativity must reckon with these new, robust restrictions.

The author acknowledges Pat Harding of the HAWC collaboration for help with the construction of this story.

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.